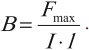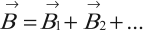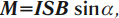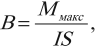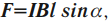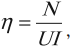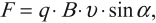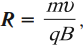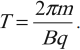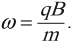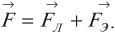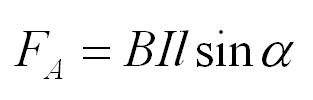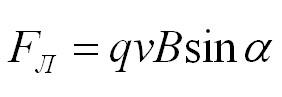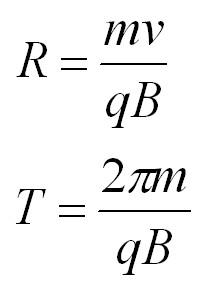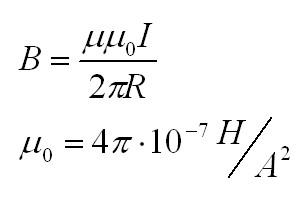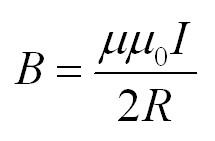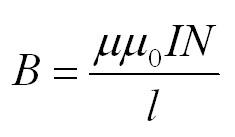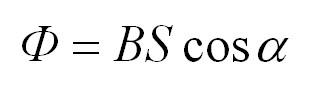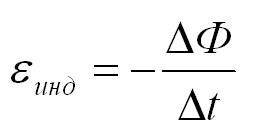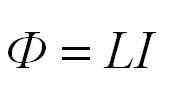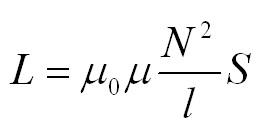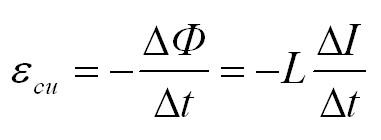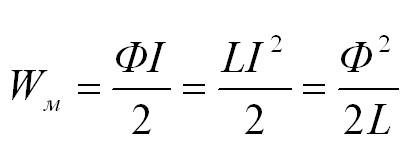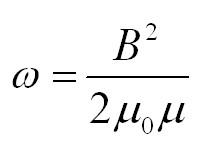рамка в магнитном поле формула

Магнитное поле

Магнитное поле – особая форма материи, существующая вокруг движущихся электрических зарядов – токов.

Источниками магнитного поля являются постоянные магниты, проводники с током. Обнаружить магнитное поле можно по действию на магнитную стрелку, проводник с током и движущиеся заряженные частицы.

Для исследования магнитного поля используют замкнутый плоский контур с током (рамку с током).

Впервые поворот магнитной стрелки около проводника, по которому протекает ток, обнаружил в 1820 году Эрстед. Ампер наблюдал взаимодействие проводников, по которым протекал ток: если токи в проводниках текут в одном направлении, то проводники притягиваются, если токи в проводниках текут в противоположных направлениях, то они отталкиваются.

Свойства магнитного поля:

Важно!
Магнитное поле не является потенциальным. Его работа на замкнутой траектории может быть не равна нулю.

Магнитным взаимодействием называют притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока.

Магнитное взаимодействие движущихся электрических зарядов объясняется так: всякий движущийся электрический заряд создает в пространстве магнитное поле, которое действует на движущиеся заряженные частицы.

Силовая характеристика магнитного поля – вектор магнитной индукции ​ \( \vec \) ​. Модуль вектора магнитной индукции равен отношению максимального значения силы, действующей со стороны магнитного поля на проводник с током, к силе тока в проводнике ​ \( I \) ​ и его длине ​ \( l \) ​:

1 Тл – это индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила 1 Н.

Направление вектора магнитной индукции совпадает с направлением от южного полюса к северному полюсу магнитной стрелки (направление, которое указывает северный полюс магнитной стрелки), свободно установившейся в магнитном поле.

Направление вектора магнитной индукции можно определить по правилу буравчика:

если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции.

Для определения магнитной индукции нескольких полей используется принцип суперпозиции:

магнитная индукция результирующего поля, созданного несколькими источниками, равна векторной сумме магнитных индукций полей, создаваемых каждым источником в отдельности:

Поле, в каждой точке которого вектор магнитной индукции одинаков по величине и направлению, называется однородным.

Наглядно магнитное поле изображают в виде магнитных линий или линий магнитной индукции. Линия магнитной индукции – это воображаемая линия, в любой точке которой вектор магнитной индукции направлен по касательной к ней.

Свойства магнитных линий:

Густота расположения позволяет судить о величине поля: чем гуще расположены линии, тем сильнее поле.

На плоский замкнутый контур с током, помещенный в однородное магнитное поле, действует момент сил ​ \( M \) ​:

где ​ \( I \) ​ – сила тока в проводнике, ​ \( S \) ​ – площадь поверхности, охватываемая контуром, ​ \( B \) ​ – модуль вектора магнитной индукции, ​ \( \alpha \) ​ – угол между перпендикуляром к плоскости контура и вектором магнитной индукции.

Тогда для модуля вектора магнитной индукции можно записать формулу:

где максимальный момент сил соответствует углу ​ \( \alpha \) ​ = 90°.

В этом случае линии магнитной индукции лежат в плоскости рамки, и ее положение равновесия является неустойчивым. Устойчивым будет положение рамки с током в случае, когда плоскость рамки перпендикулярна линиям магнитной индукции.

Взаимодействие магнитов

Постоянные магниты – это тела, длительное время сохраняющие намагниченность, то есть создающие магнитное поле.

Основное свойство магнитов: притягивать тела из железа или его сплавов (например стали). Магниты бывают естественные (из магнитного железняка) и искусственные, представляющие собой намагниченные железные полосы. Области магнита, где его магнитные свойства выражены наиболее сильно, называют полюсами. У магнита два полюса: северный ​ \( N \) ​ и южный ​ \( S \) ​.

Важно!
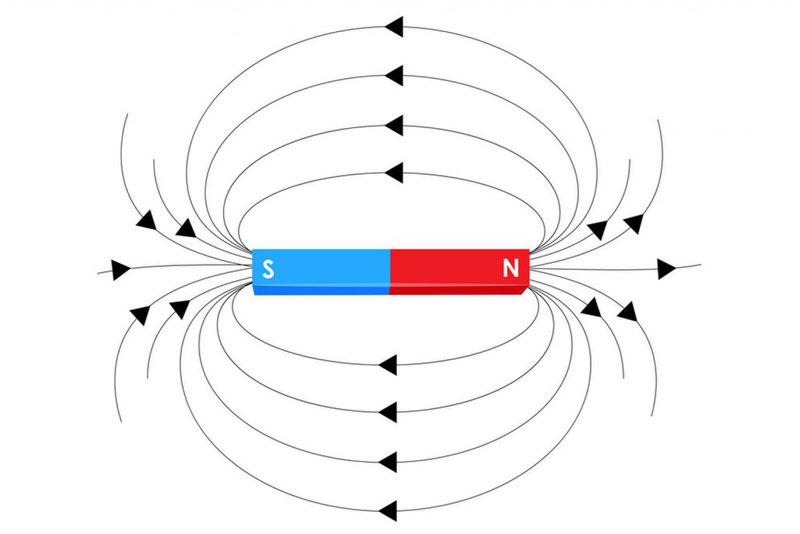
Вне магнита магнитные линии выходят из северного полюса и входят в южный полюс.

Разделить полюса магнита нельзя.

Объяснил существование магнитного поля у постоянных магнитов Ампер. Согласно его гипотезе внутри молекул, из которых состоит магнит, циркулируют элементарные электрические токи. Если эти токи ориентированы определенным образом, то их действия складываются и тело проявляет магнитные свойства. Если эти токи расположены беспорядочно, то их действие взаимно компенсируется и тело не проявляет магнитных свойств.

Магниты взаимодействуют: одноименные магнитные полюса отталкиваются, разноименные – притягиваются.

Магнитное поле проводника с током

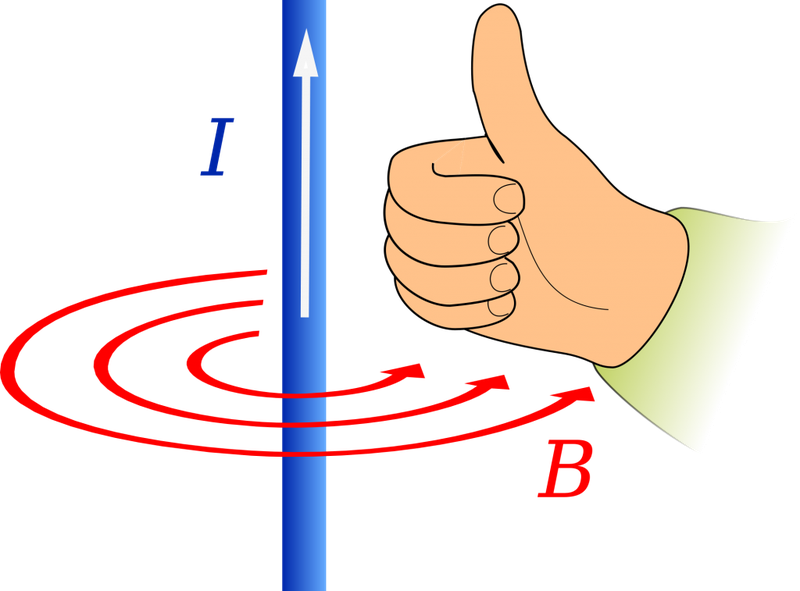
Электрический ток, протекающий по проводнику с током, создает в окружающем его пространстве магнитное поле. Чем больше ток, проходящий по проводнику, тем сильнее возникающее вокруг него магнитное поле.

Магнитные силовые линии этого поля располагаются по концентрическим окружностям, в центре которых находится проводник с током.

Направление линий магнитного поля вокруг проводника с током всегда находится в строгом соответствии с направлением тока, проходящего по проводнику.

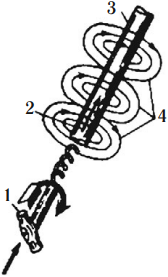
Направление магнитных силовых линий можно определить по правилу буравчика: если поступательное движение буравчика (1) совпадает с направлением тока (2) в проводнике, то вращение его рукоятки укажет направление силовых линий (4) магнитного поля вокруг проводника.

При изменении направления тока линии магнитного поля также изменяют свое направление.

По мере удаления от проводника магнитные силовые линии располагаются реже. Следовательно, индукция магнитного поля уменьшается.

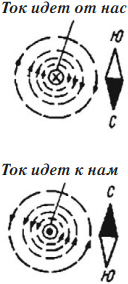
Направление тока в проводнике принято изображать точкой, если ток идет к нам, и крестиком, если ток направлен от нас.

Для получения сильных магнитных полей при небольших токах обычно увеличивают число проводников с током и выполняют их в виде ряда витков; такое устройство называют катушкой.

В проводнике, согнутом в виде витка, магнитные поля, образованные всеми участками этого проводника, будут внутри витка иметь одинаковое направление. Поэтому интенсивность магнитного поля внутри витка будет больше, чем вокруг прямолинейного проводника. При объединении витков в катушку магнитные поля, созданные отдельными витками, складываются. При этом концентрация силовых линий внутри катушки возрастает, т. е. магнитное поле внутри нее усиливается.

Чем больше ток, проходящий через катушку, и чем больше в ней витков, тем сильнее создаваемое катушкой магнитное поле. Магнитное поле снаружи катушки также складывается из магнитных полей отдельных витков, однако магнитные силовые линии располагаются не так густо, вследствие чего интенсивность магнитного поля там не столь велика, как внутри катушки.

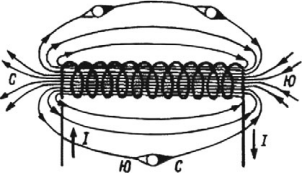
Магнитное поле катушки с током имеет такую же форму, как и поле прямолинейного постоянного магнита: силовые магнитные линии выходят из одного конца катушки и входят в другой ее конец. Поэтому катушка с током представляет собой искусственный электрический магнит. Обычно для усиления магнитного поля внутрь катушки вставляют стальной сердечник; такую катушку называют электромагнитом.

Направление линий магнитной индукции катушки с током находят по правилу правой руки:

если мысленно обхватить катушку с током ладонью правой руки так, чтобы четыре пальца указывали направление тока в ее витках, тогда большой палец укажет направление вектора магнитной индукции.

Для определения направления линий магнитного поля, создаваемого витком или катушкой, можно использовать также правило буравчика:

если вращать ручку буравчика по направлению тока в витке или катушке, то поступательное движение буравчика укажет направление вектора магнитной индукции.

Электромагниты нашли чрезвычайно широкое применение в технике. Полярность электромагнита (направление магнитного поля) можно определить и с помощью правила правой руки.

Сила Ампера

Сила Ампера – сила, которая действует на проводник с током, находящийся в магнитном поле.

Закон Ампера: на проводник c током силой ​ \( I \) ​ длиной ​ \( l \) ​, помещенный в магнитное поле с индукцией ​ \( \vec \) ​, действует сила, модуль которой равен:

где ​ \( \alpha \) ​ – угол между проводником с током и вектором магнитной индукции ​ \( \vec \) ​.

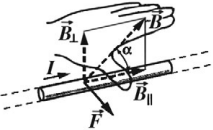
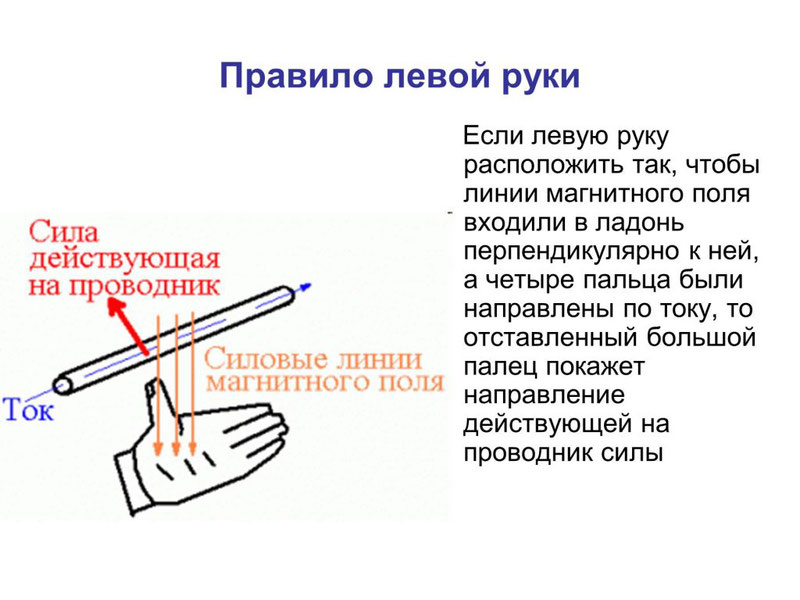
Направление силы Ампера определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​ \( B_\perp \) ​ входила в ладонь, а четыре вытянутых пальца указывали направление тока в проводнике, то отогнутый на 90° большой палец покажет направление силы Ампера.

Сила Ампера не является центральной. Она направлена перпендикулярно линиям магнитной индукции.

Сила Ампера широко используется. В технических устройствах создают магнитное поле с помощью проводников, по которым течет электрический ток. Электромагниты используют в электромеханическом реле для дистанционного выключения электрических цепей, магнитном подъемном кране, жестком диске компьютера, записывающей головке видеомагнитофона, в кинескопе телевизора, мониторе компьютера. В быту, на транспорте и в промышленности широко применяют электрические двигатели. Взаимодействие электромагнита с полем постоянного магнита позволило создать электроизмерительные приборы (амперметр, вольтметр).

Простейшей моделью электродвигателя служит рамка с током, помещенная в магнитное поле постоянного магнита. В реальных электродвигателях вместо постоянных магнитов используют электромагниты, вместо рамки – обмотки с большим числом витков провода.

Коэффициент полезного действия электродвигателя:

где ​ \( N \) ​ – механическая мощность, развиваемая двигателем.

Коэффициент полезного действия электродвигателя очень высок.

Алгоритм решения задач о действии магнитного поля на проводники с током:

Сила Лоренца

Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля.

Формула для нахождения силы Лоренца:

где ​ \( q \) ​ – заряд частицы, ​ \( v \) ​ – скорость частицы, ​ \( B \) ​ – модуль вектора магнитной индукции, ​ \( \alpha \) ​ – угол между вектором скорости частицы и вектором магнитной индукции.

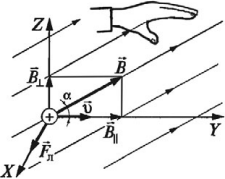
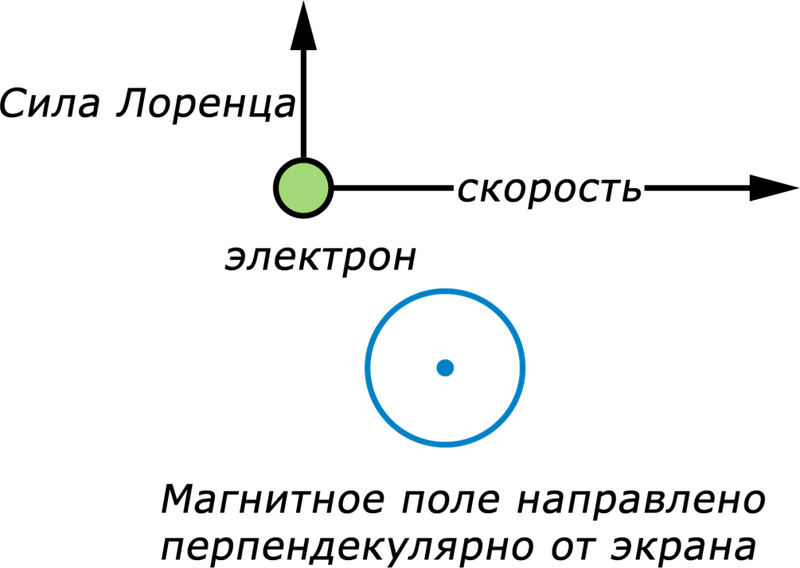
Направление силы Лоренца определяют по правилу левой руки: если ладонь левой руки расположить так, чтобы перпендикулярная к проводнику составляющая вектора магнитной индукции ​ \( B_\perp \) ​ входила в ладонь, а четыре вытянутых пальца указывали направление скорости положительно заряженной частицы, то отогнутый на 90° большой палец покажет направление силы Лоренца.

Если заряд частицы отрицательный, то направление силы изменяется на противоположное.

Важно!
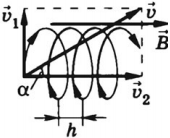
Если вектор скорости сонаправлен с вектором магнитной индукции, то частица движется равномерно и прямолинейно.

В однородном магнитном поле сила Лоренца искривляет траекторию движения частицы.

Если вектор скорости перпендикулярен вектору магнитной индукции, то частица движется по окружности, радиус которой равен:

где ​ \( m \) ​ – масса частицы, ​ \( v \) ​ – скорость частицы, ​ \( B \) ​ – модуль вектора магнитной индукции, ​ \( q \) ​ – заряд частицы.

В этом случае сила Лоренца играет роль центростремительной и ее работа равна нулю. Период (частота) обращения частицы не зависит от радиуса окружности и скорости частицы. Формула для вычисления периода обращения частицы:

Угловая скорость движения заряженной частицы:

Важно!
Сила Лоренца не меняет кинетическую энергию частицы и модуль ее скорости. Под действием силы Лоренца изменяется направление скорости частицы.

Важно!
Если частица движется в электрическом и магнитном полях, то полная сила Лоренца равна:

Особенности движения заряженной частицы в магнитном поле используются в масс-спектрометрах – устройствах для измерения масс заряженных частиц; ускорителях частиц; для термоизоляции плазмы в установках «Токамак».

Алгоритм решения задач о действии магнитного (и электрического) поля на заряженные частицы:

Источник

Магнетизм для чайников: основные формулы, определение, примеры

Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.

Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Магнетизм: определение

Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.

Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

Изображение магнитного поля при помощи силовых линий

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

Сила Ампера

Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:

Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

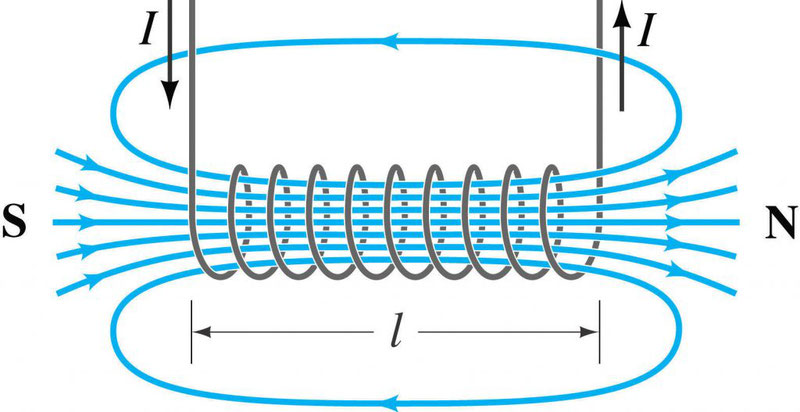
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Магнитный поток и ЭДС

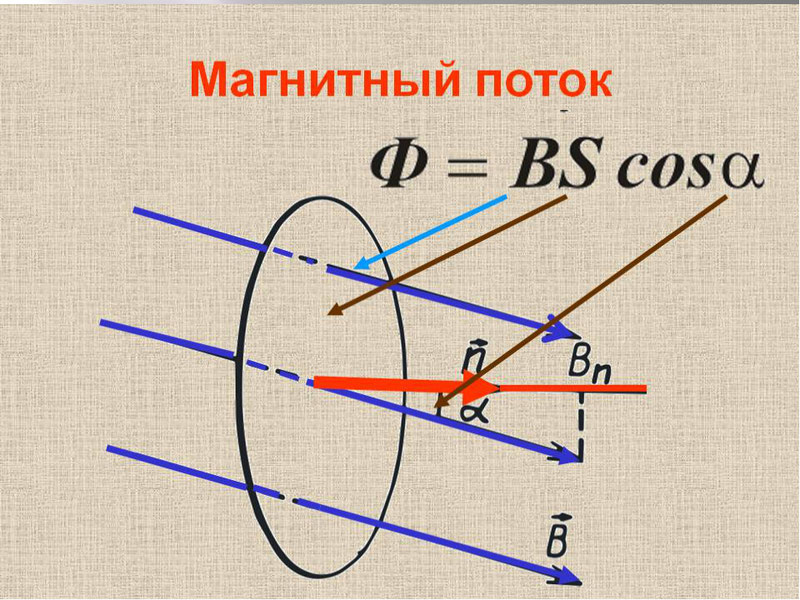
Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.

S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.

При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.

По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.

Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:

L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:

Формула для ЭДС самоиндукции:

Энергия магнитного поля

Объемная плотность энергии поля:

Источник

Рамка в магнитном поле формула

По двум длинным прямолинейным и параллельным проводам, расстояние между которыми d = 4 см, в противоположных направлениях текут токи I₁ = 0,3 А, I₂ = 0,5 А. Найти магнитную индукцию поля в точке А, которая находится на расстоянии r = 2 см от первого и провода на продолжении линии, соединяющей провода (рис.8).

Решение.

На рис. 8 провода расположены перпендикулярно плоскости чертежа. Маленькими кружочками изображены сечения проводив. Условимся, что ток I₁, течет к нам, а ток I₂ –&nbsp от нас. Общая индукция В в точке А равна векторной (геометрической) сумме индукции В₁, и В₁ полей, создаваемых каждым током в отдельности т. е,

Для того чтобы найти направление вектора В₁ и В₂, проведем через точку А силовые линии магнитных полей, созданных токами I₁ и I₂.

Силовые линии магнитного поля прямого провода с током представляют собой концентрические окружности с центром на оси провода. Направление силовой линии совпадает с движением концов рукоятки правого буравчика, ввинчиваемого во направлению тока (правило буравчика) Поэтому силовая линия магнитного поля тока I₁, проходящая через точку А, представляет собой окружность радиусом I₁ A, а силовая линии магнитного поля тока I₂, проходящая через эту же точку, — окружность радиусом I₂ A (на рис. 8 показана только часто этой окружности). По правилу буравчика находим, что силовая линия магнитного ноля тока I₁ направлена против часовой стрелки, а тока I₂ – по часовой стрелке.

Теперь легко найти направления векторов В₁ и В₂ в точке А: каждый из них направлен по касательной к соответствующей силовой линии в этой точке. Так как векторы В₁ и В₂ направлены вдоль одной прямой в противоположные стороны, то векторное равенство (1) можно заменить алгебраическим равенством

Индукция магнитного поля тока I, текущего по прямому бесконечно длинному проводу, вычисляется по формуле

где μ₀ –&nbsp магнитная постоянная; μ –&nbsp магнитная пропицаемость среды, в которой провод расположен; r –&nbspрасстояние от провода до точки, в которой определяется индукция. Подставив выражения В₁ и В₂ в равенство (2), получим

Пример 2.

Из проволоки диаметром d = 0,01 мм и сопротивлением r = 25 Ом намотан соленоид на картонном цилиндре (витки вплотную прилегают друг к другу). Определить индукцию магнитного поля на оси соленоида, если напряжение на концах обмотки U = 2 В.

Индукция магнитного поля на оси соленоида вычисляется по формуле

Здесь n = 1/d; d – диаметр проволоки; n – число витков на единицу длины соленоида; I – сила тока, текущего по обмотке соленоида. Силу тока, текущего по обмотке, найдём по закону Ома для участка цепи:

Подставим значения n и I в равенство (1):

Пример 3.

Прямой провод длиной l = 10 см, по которому течет ток I = 0,5 А, помещен в однородное магнитное поле перпендикулярно силовым линиям. Найти индукцию магнитного поля, если оно действует на прямой провод с силой F = 2,6 мН.

Сила, с которой однородное магнитное поле действует на прямой провод с током, вычисляется по закону Ампера:

где I – сила тока, текущего по проводнику; l – длина проводника; В – индукция магнитного поля, в которое проводник помещён; а- угол между направлениями тока и линий индукции. Из формулы (1) найдем

Пример 4.

Протон, пройдя ускоряющую разность потенциалов U = 400 В, влетел в однородное магнитное поле с индукцией В = 0,2 Тл и начал двигаться по окружности. Вычислить радиус окружности.

Направление силы Лоренца подчиняется, как известно, правилу левой руки. Угол между направлениями v и F_л всегда составляет 90º. Следовательно, сила Лоренца является центростремительной силой, т.е. или

где m – масса протона; R – радиус окружности, по которой движется протон. Тогда

Протон получил скорость, пройдя, ускоряющую разность потенциалов По закону сохранения энергии работа, совершенная полем при перемещении протона, равна кинетической энергии, приобретенной протоном, т, е.

Работа сил электрического поля при перемещении протона определяется по формуле

Кинетическая энергия протона

Подставляя выражение для v в (1), находим

Проверим расчетную формулу (6):

Пример 5.

Ток, текущий в рамке, содержащей N витков, создаст магнитное поле. В центре рамки индукция поля B = 0,126 Тл. магнитный момент рамки, если ее радиус R = 10 см.

Магнитный момент рамки с током

Выпишем числовые значения величин, входящих в (2), в СИ: Вычислим искомый магнитный момент:

Пример 6.

Используя понятие угловой скорости вращении (ω = 2π/T = 2πn, где T – период вращения; n – частота вращения), определим частоту вращения рамки:

Угловую скорость вращения найдем из соотношения

Подставив выражение &#969 по (3) в (1),получаем

Выразим значения ряда величин, входящих в формулу (4), в СИ: Выполним вычисления:

Пример 7.

На немагнитный каркас длиной l = 50 см и площадью сечения S = 3см 2 намотан в одни слой провод диаметром d = 0,4 мм так, что витки плотно прилегают друг к другу. Найти: 1) индуктивность получившегося соленоида и 2) магнитный поток, пронизывающий поперечное сечение соленоида при токе силой I = 1 А.

Индуктивность соленоида вычисляется по формуле

где n – число витков, приходящихся на единицу длины соленоида; V – объем соленоида. Число витков n получим, разделив единицу длины на диаметр провода:

Объем соленоида V = Sl, где S – площадь поперечного сечения соленоида; l – длина соленоида. Подставим выражения для n и V в равенство (1):

Выпишем числовые значения величин, входящих в (3), в СИ:

При наличии тока в соленоиде любое его поперечное сечение пронизывает магнитный поток

где В – магнитная индукция в соленонде. Магнитная индукция соленоида определяется по формуле

Подставив выражения n и В по (2) и (5) в (4), получим расчетную формулу

Выполним вычисления, подставив в расчетную формулу значения величин I, S и d в СИ:

Пример 8.

Из формулы емкости плоского конденсатора

(ε₀ – электрическая постоянная; ε – диэлектрическая проницаемость среды мёжду пластинами конденсатора; S – площадь пластины конденсатора; d – расстояние между пластинами) может быть найдено искомое расстояние

Из формулы Томсона, определяющей период колебаний Т в колебательном контуре, найдем емкость ), где L – индуктивность катушки. Подставив это выражение С в (1), получим

Выразим некоторые величины, входящие в расчетную формулу (4), в СИ:

Источник