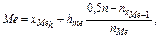какие графики используются для наглядного представления вариационного ряда

Графическое изображение рядов распределения: полигон, гистограмма. Показатели центра распределения, колеблемости признака. Формы распределения.

Поможем написать любую работу на аналогичную тему

Графики являются наглядной формой отображения рядов распределения. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат.

Для графического представления атрибутивных рядов распределения используются различные диаграммы: столбиковые, линейные, круговые, фигурные, секторные и т. д.

Для дискретных вариационных рядов графиком является полигон распределения.

Полигоном распределения называется ломаная линия, соединяющая точки с координатами или где — дискретное значение признака, — частота, — частость.

График строится в принятом масштабе. Вид полигона распределения приведен на рис. 5.1.

При построении графиков рядов распределения большое значение имеет соотношение масштабов по оси абсцисс и оси ординат. В этом случае и необходимо руководствоваться «правилом золотого сечения», в соответствии с которым высота графика должна быть примерно в два раза меньше его основания.

При проведении эмпирического исследования ряда распределения рассчитываются и анализируются следующие группы показателей:

• показатели положения центра распределения;

• показатели степени его однородности;

• показатели формы распределения.

Показатели положения центра распределения. К ним относятся степенная средняя в виде средней арифметической и структурные средние – мода и медиана.

Средняя арфметическая для дискретного ряда распределения рассчитывается по формуле:

В отличие от средней арифметической, рассчитываемой на основе всех вариант, мода и медиана характеризует значение признака у статистической единице, занимающей определенное положение в вариационном ряду.

Медиана (Me) — значение признака у статистической единицы, стоящей в середине ранжированного ряда и делящей совокупность на две равные по численности части.

Медиану используют как наиболее надежный показатель типичного значения неоднородной совокупности, так как она нечувствительна к крайним значениям признака, которые могут значительно отличаться от основного массива его значений. Кроме этого, медиана находит практическое применение вследствие особого математического свойства: Рассмотрим определение моды и медианы на следующем примере: имеется ряд распределения рабочих участка по уровню квалификации.

Данные приведены в таблице 5.2.

Мода выбирается по максимальному значению частоты: при nmax = 14 Mo=4, т.е. чаще всего встречается 4-ый разряд. Для нахождения медианы Me определяются центральные единицы Это 25 и 26-ая единицы. По накопленным частотам определяется группа, в которую попадают эти единицы. Это 4-ая группа, в которой значение признака равно 4. Таким образом, Me = 4, это означает, что у половины рабочих разряд ниже 4-го, а у другой – выше четвертого. В интервальном ряду значения Mo и Me вычисляются более сложным путем.

Мода определяется следующим образом:

• По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.

• Внутри модального интервала значение моды вычисляется по формуле:

Для расчета медианы в интервальных рядах используется следующий подход:

• По накопленным частотам находится медианный интервал. Медианным называется интервал, содержащий центральную единицу.

• Внутри медианного интервала значение Me определяется по формуле:

В неравноинтервальных рядах при вычислении Mo используется другая частотная характеристика – абсолютная плотность распределения:

Расчет моды и медианы для интервального ряда распределения рассмотрим на примере ряда распределения рабочих по стажу, приведенного в таблице 5.3.

• Максимальная частота n max = 13, она соответствует четвертой группе, следовательно, модальным является интервал с границами 12 – 16 лет.

• Моду рассчитаем по формуле:

Чаще всего встречаются рабочие со стажем работы около 13 лет. Мода не находится в середине модального интервала, она смещена к его нижней границе, связано это со структурой данного ряда распределения (частота предмодального интервала значительно больше частоты постмодального интервала).

• По графе накопленных частот определяется медианный интервал. Он содержит 25 и 26-у статистические единицы, которые находятся в разных группах – в 3-ей и 4-ой. Для нахождения Me можно использовать любую из них. Расчет проведем по 3-ей группе:

Такое же значение Me можно получить при её расчете по 4-ой группе:

Для нахождения моды в интервальном ряду правую вершину модального прямоугольника нужно соединить с правым верхним углом предыдущего прямоугольника, а левую вершину – с левым верхним углом последующего прямоугольника. Абсцисса точки пересечения этих прямых и будет модой распределения.

Для определение медианы высоту наибольшей ординаты кумуляты, соответствующей общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения является медианой.

Кроме Mo и Me в вариантных рядах могут быть определены и другие структурные характеристики – квантили. Квантили предназначены для более глубокого изучения структуры ряда распределения. Квантиль – это значение признака, занимающее определенное место в упорядоченной по данному признаку совокупности. Различают следующие виды квантилей:

• квартили – значения признака, делящие упорядоченную совокупность на 4 равные части;

• децили – значения признака, делящие совокупность на 10 равных частей;

Рассчитаем квартили для ряда распределения рабочих участка по стажу работы:

Следовательно, у четверти рабочих стаж менее 7 лет и у четверти – более 16 лет. Таким образом, для характеристики положения центра ряда распределения можно использовать 3 показателя: среднее значение признака, мода, медиана.

При выборе вида и формы конкретного показателя центра распределения необходимо исходить из следующих рекомендаций:

• для устойчивых социально-экономических процессов в качестве показателя центра используют среднюю арифметическую. Такие процессы характеризуются симметричными распределениями, в которых

• для неустойчивых процессов положение центра распределения характеризуется с помощью Mo или Me. Для асимметричных процессов предпочтительной характеристикой центра распределения является медиана, поскольку занимает положение между средней арифметической и модой.

Вторая важнейшая задача при определении общего характера распределения – это оценка степени его однородности. Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака, т.е. несовпадением его значений у разных статистических единиц. Для измерения вариации в статистике используются абсолютные и относительные показатели. Выяснение общего характера распределения предполагает не только оценку степени его однородности, но и исследование формы распределения, т.е. оценку симметричности и эксцесса.

Из математической статистики известно, что при увеличении объема статистической совокупности и одновременного уменьшении интервала группировки полигон либо гистограмма распределения все более и более приближается к некоторой плавной кривой, являющейся для указанных графиков пределом. Эта кривая называется эмпирической кривой распределения и представляет собой графическое изображение в виде непрерывной линии изменения частот, функционально связанного с изменением вариант.

В статистике различают следующие виды кривых распределения:

• одновершинные кривые; • многовершинные кривые.

Однородные совокупности описываются одновершинными распределениями. Многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.

Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.

Распределение называется симметричным, если частоты любых 2-х вариантов, равноотстоящих в обе стороны от центра распределения, равны между собой. В таких распределениях

Для характеристики асимметрии используют коэффициенты асимметрии.

Наиболее часто используются следующие из них:

• Коэффициент асимметрии Пирсона

Рис. 5.4.Правосторонняя асимметрия Рис. 5.5. Левосторонняя асимметрия

Чем ближе по модулю As к 1, тем асимметрия существеннее:

Коэффициент асимметрии Пирсона характеризует асимметрию только в центральной части распределения, поэтому более распространенным и более точным является коэффициент асимметрии, рассчитанный на основе центрального момента 3-его порядка:

Центральным моментом в статистике называется среднее отклонение индивидуальных значений признака от его среднеарифметической величины.

Центральный момент k-ого порядка рассчитывается как:

Соответственно формулы для определения центрального момента третьего порядка имеют следующий вид:

Для оценки существенности рассчитанного вторым способом коэффициента асимметрии определяется его средняя квадратическая ошибка:

Для одновершинных распределений рассчитывается еще один показатель оценки его формы – эксцесс. Эксцесс является показателем островершинности распределения. Он рассчитывается для симметричных распределений на основе центрального момента 4-ого порядка

При симметричных распределениях Ех=0. если Ех>0, то распределение относится к островершинным, если Ех

Источник

Графическое представление вариационных рядов

Для более наглядного представления временных рядов используют следующие виды графиков.

1. Полигонраспределения представляет собой график частот. Это ломаная линия, абсциссы вершин которой соответствуют вариантам, а ординаты – частотам. Обычно его используют для дискретных вариационных рядов. На рисунке 17 представлен полигон распределения для вариационного ряда, приведенного в таблице 5.

2. Кумулятапредставляет собой график накопленных частот (ее еще называюткумулятивной кривой). На рисунке 17 представлена кумулята для того же самого ряда.

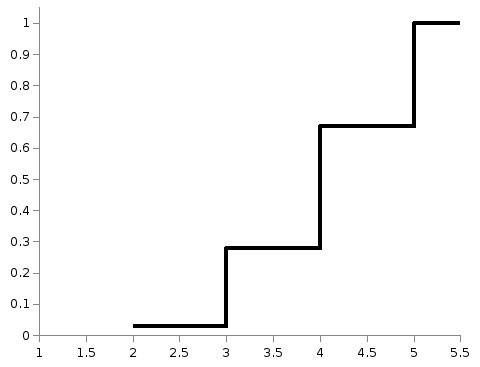
3. График эмпирической функции распределенияпредставляет собой график накопленных относительных частот, т.е. относительных частот того, что признак принял значение, меньшее заданного. Для примера из таблицы 5 он представлен на рисунке 18 (рекомендуется сравнить с графиком функции распределения, которая рассматривалась при изучении теории вероятностей).

4. Гистограмма распределения представляет собой фигуру, составленную из прямоугольников, каждый из которых соответствует интервалу сгруппированного ряда, а их высота равна соответствующим частотам. Для примера из таблицы 4 гистограмма распределения представлена на рисунке 19.

Для сгруппированного ряда можно также построить полигон распределения (соединив отрезками середины верхних оснований прямоугольников гистограммы) и кумуляту (см. рисунок 19).

Показатели вариации Средние вариационного ряда

Основным показателем вариации называется среднее арифметическоевариационного ряда, которое рассчитывается по формуле:

,

где n– общее число наблюдений;

w_i– относительная частота варианты х_i.

Например, для таблицы 5 среднее арифметическое 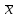= (2*3 + 3* 25 + 4*39 + 5*33) = 4,02 (балла).

Свойства этой средней величины аналогичны свойствам математического ожидания.

Кроме того, если вариационный ряд разбит на несколько групп, то среднее арифметическое всего ряда можно рассчитать, как среднее арифметическое групповых средних: ,

где n– общее число наблюдений;

— среднее арифметическоеi-й группы;

n_i– число наблюдений вi-й группе.

Если всех студентов, данные о которых приведены в таблице 5, выстроить в ряд по возрастанию полученного ими балла, то из этих ста человек в середине стояли бы студенты под номерами 50 и 51 от начала ряда. Оба эти студента получили оценку 4, так как накопленная частота для оценки 3 составляет 28, а для оценки 4 она составляет 67 (все студенты под номерами с 29-го по 67-й включительно получили оценку 4).

То значение варианты, которое соответствует середине вариационного ряда, называется медианойи обозначаетсяMe. Если число наблюдений – нечетное, то медианный номер равен (n+ 1)/2; а если четное – то медианных номеров два:n/2 и ((n/2) +1), а сама медиана рассчитывается, как среднее арифметическое этих двух вариант.

В примере из таблицы 5 медианные номера 50 и 51, а Me= (4 + 4)/2 = = 4 (балла).

Та варианта, которая встречается в вариационном ряду чаще всего, называется модой(мода – это то значение признака, которое встречается у большинства наблюдений) и обозначаетсяMo.

В таблице 5 Mo= 4 (балла), так как этой варианте соответствует наибольшая частота 39.

Для интервального вариационного ряда используется несколько более сложная методика расчета рассмотренных средних, которую здесь рассматривать не будем.

В вышеприведенном примере Мо = Ме = 4 4,02 =. Это отнюдь не всегда бывает так. Например, если рассчитать средние по данным таблицы 6, то можно получить= 3,814,Me= 3,Mo= 5. Т.е. при том, что большинство студентов получили 5 (42 человека), в середине ряда оказались студенты с оценкой 3, а средний балл составил чуть меньше 4.

Источник

Графическое представление вариационных рядов

Для повышения наглядности вариационных рядов, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма и полигон частот.

Гистограмма

Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте (или относительной частоте) попадания в данный интервал. Если ряд безинтервальный, то ширина всех столбцов выбирается произвольной, но одинаковые.

На графике гистограммы основание прямоугольников откладывается по оси x, а высота — по оси у прямоугольной системы координат.

Рис 7.1. Гистограмма количества нарушений скорости (пример 6.3.)

Рис. 7.2. Гистограмма итогов сдачи экзамена (пример 6.4.)

Полигон частот

Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у.

Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых.

Полигончастот используется для представления распределений как непрерывных, так и дискретных признаков. В случае непрерывного распределения полигон частот является более предпочтительным способом графического представления, чем гистограмма, если график эмпирического распределения описывается плавной зависимостью.

Рис. 7.3. Полигон частот итогов сдачи экзамена (пример 6.4.)

Эмпирическая функция распределения

Эмпирической функцией распределения называется функция F*(х), определяющая для каждого значения х относительную частоту события X 10.

при х 10.

Построим график полученной функции.

Рис. 7.4 График эмпирической функции

Числовые характеристики выборки

Вариационные ряды и графики эмпирических распределений дают наглядное представление о том, как варьирует признак в выборочной совокупности. Но они недостаточны для полной характеристики выборки, поскольку содержат много деталей, охватить которые невозможно без применения обобщающих числовых характеристик.

Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой.

Характеристики положения

Чаще всего употребляются такие характеристики положения, как среднее арифметическое, медиана и мода.

Среднее арифметическое

Среднее арифметическое, или просто среднее, — одна из основных характеристик выборки.

Среднее арифметическое – такое значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учетом знака отклонения).

Среднее принято обозначать той же буквой, что и варианты выборки, с той лишь разницей, что над буквой ставится символ усреднения — черта. Например, если обозначить исследуемый признак через X, а его числовые значения — через x_i, то среднее арифметическое имеет обозначение .

Среднее арифметическое, как и другие числовые характеристики выборки, может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных.

Для несгруппированных данных среднее арифметическое определяется по следующей формуле:

где n — объем выборки;

Если данные сгруппированы, то

где n — объем выборки;

k — число интервалов группировки;

х_i — срединное значение i-ого интервала.

Среднее арифметическое – величина того же наименования, что и значения признаков.

Нахождение среднего арифметического непрерывного вариационного ряда осложняется, если крайние интервалы не замкнуты (то есть имеют вид «менее 10» или «более 60»). В этом случае считается, что ширина первого интервала равна ширине второго, а ширина последнего – ширине предпоследнего.

Среднее арифметическое, вычисленное по формуле называют также взвешенным средним, подчеркивая этим, что в формуле x_i, суммируются с коэффициентами (весами), равными частотам попадания в интервалы группировки.

Медиана

Медианой (Ме) называется такое значение признака X, когда ровно половина значений экспериментальных данных меньше ее, а вторая половина — больше.

Если данных немного (объем выборки невелик), медиана вычисляется очень просто. Для этого выборку ранжируют, т. е. располагают данные в порядке возрастания или убывания, и в ранжированной выборке, содержащей n членов, ранг R (порядковый номер) медианы определяется как

Пример 7.8. Имеется ранжированная выборка, содержащая нечетное число членов n = 9:

12, 14, 14, 18, 20, 22, 22, 26, 28.

Тогда ранг медианы:

и медиана совпадает с пятым членом ряда: Ме = 20.

Если выборка содержит четное число членов, то медиана не может быть определена столь однозначно.

Пример 7.9. Имеется ранжированная выборка, содержащая 10 членов:

6, 8, 10, 12, 14, 16, 18, 20, 22, 24.

Ранг медианы оказывается равным:

Медианой в этом случае может быть любое число между 14 и 16 (5-м и 6-м членами ряда). Для определенности принято считать в качестве медианы среднее арифметическое этих значений, т. е.:

Если необходимо найти медиану для сгруппированных данных, то поступают следующим образом. Вначале находят интервал группировки, в котором содержится медиана, путем подсчета накопленных частот или накопленных относительных частот.

Медианным будет тот интервал, в котором накопленная частота впервые окажется больше или накопленная относительная частота — больше 0,5. Внутри медианного интервала медиана определяется по следующей формуле:

где — нижняя граница медианного интервала;

h_me — ширина медианного интервала;

— накопленная частота интервала, предшествующего медианному,

— частота медианного интервала.

Пример 7.10. Найти медиану для интервального ряда примера 6.3.

Объем выборки равен п = 50 + 32 + 26 + 11 + 5 = 124.

Найдем медианный интервал – интервал, в котором накопленная частота впервые окажется больше 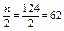или накопленная относительная частота — больше 0,5.

Так как, накопительная частота второго интервала 50 + 32 = 82 > 62, то следовательно интервал (30; 40) будет медианным и = 30, h_me = 40 – 30 = 10, = 50, = 32.

Медиана обычно несколько отличается от среднего арифметического. Так бывает всегда, когда имеет место несимметричная форма эмпирического распределения.

Мода

Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

Ряд называется унимодальным, если в нем только одно модальное значение и полимодальным, если есть несколько значений признака, которые встречаются одинаково часто. Для полимодального ряда моду не вычисляют.

Для дискретного ряда мода находится по определению.

Интервал группировки с наибольшей частотой называется модальным.

Для определения моды в интервальном ряду используется следующая формула:

где — нижняя граница модального интервала;

h — ширина интервала группировки;

n_Mo — частота модального интервала;

n_Mo-1 — частота интервала, предшествующего модальному;

n_Mo+1 — частота интервала, следующего за модальным.

Характеристики рассеяния

Средние значения не дают полной информации о варьирующем признаке. Нетрудно представить себе два эмпирических распределения, у которых средние одинаковы, но при этом у одного из них значения признака рассеяны в узком диапазоне вокруг среднего, а у другого – в широком. Поэтому наряду со средними значениями вычисляют и характеристики рассеяния выборки. Рассмотрим наиболее употребительные из них.

Размах вариации

Размах вариации – разность между максимальной и минимальной вариантами выборки:

.

Как видим, размах вычисляется очень просто, и в этом его главное и единственное достоинство. Информативность этого показателя невелика. Можно привести очень много распределений, сильно отличающихся по форме, но имеющих одинаковый размах. Размах вариации используется иногда в практических исследованиях при малых (не более 10) объемах выборки, Например, по размаху вариации легко оценить, насколько различаются лучший и худший результаты в группе спортсменов. При больших объемах выборки к его использованию надо откоситься с осторожностью.

Источник