какие два угла называют равными

ВОПРОСЫ

1. Какую фигуру называют углом?

2. Какие два угла называют равными?

3. Как называют луч, который делит угол на два равных угла?

Луч, который делит угол на два равных угла, называют биссектрисой данного угла.

РЕШАЕМ УСТНО

1. Каких чисел не хватает в цепочке вычислений?

2. Решите уравнение:

3. Корнем каких из следующих уравнений является число 5:

4. У Пети и Миши было поровну конфет. Петя отдал Мише 8 конфет. На сколько у Миши стало больше конфет, чем у Пети?

У Миши стало на 8 конфет больше, чем у Пети.

УПРАЖНЕНИЯ

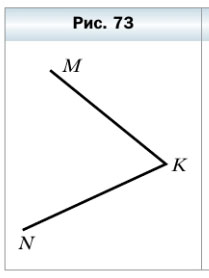
281. Как можно обозначить угол, изображенный на рисунке 73?

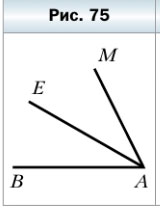
283. Назовите все углы, изображенные на рисунке 75.

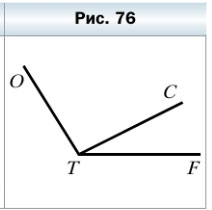
284. Запишите все углы, изображенные на рисунке 76.

285. Какие из лучей, изображенных на рисунке 77, пересекают сторону угла ВОС?

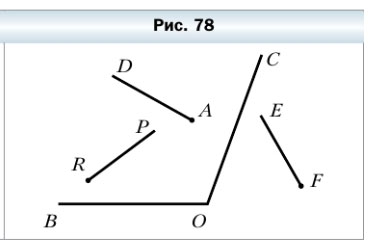
286. Какие из лучей, изображенных на рисунке 78, пересекают сторону угла ВОС?

287. Начертите MNE и проведите лучи NA и NC между его сторонами. Запишите все образовавшиеся углы.

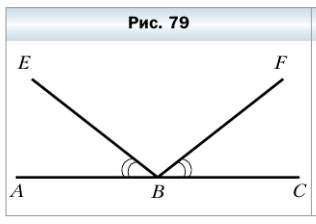
288. На рисунке 79 АВЕ = СВF. Есть ли еще на этом рисунке равные углы?

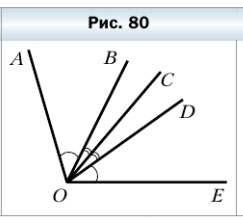
289. На рисунке 80 АОВ = DОЕ, ВОС = СОD. Есть ли еще на этом рисунке равные углы?

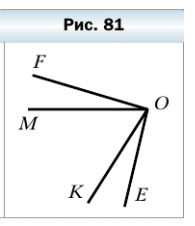
290. На рисунке 81 углы FОК и МОЕ равны. Какие еще углы, изображенные на этом рисунке, равны?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ

291. Составьте числовое выражение и найдите его значение: 1) произведение суммы чисел 18 и 20 и числа 8; 2) частное от деления разности чисел 128 и 29 на число 11; 3) частное от деления произведения чисел 15 и 6 на их разность.

292. Решите уравнение:

294. Учащиеся пятых классов ехали на двух автобусах на экскурсию. Когда из одного автобуса, в котором было 42 учащихся, восемь учащихся перешли во второй автобус, то в обоих автобусах учащихся стало поровну. Сколько учащихся было во втором автобусе сначала?

ЗАДАЧА ОТ МУДРОЙ СОВЫ

295. На озере начали распускаться кувшинки. Каждый день количество кувшинок увеличивалось вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?

Половина озера была покрыта кувшинками на 19 день.

Источник

Мерзляк 5 класс — § 11. Угол. Обозначение углов

Вопросы к параграфу

1. Какую фигуру называют углом? — Углом называют фигуру, образованную двумя лучами, имеющими общее начало.

2. Какие два угла называют равными? — Два угла называют равными, если они совпадают при наложении.

3. Как называют луч, который делит угол на два равных угла? — биссектриса.

Комментарий: Запомнить это сложное слово поможет шутка: «Биссектриса — это крыса, которая бегает по углам и делит угол пополам».

Решаем устно

1. Каких чисел не хватает в цепочке вычислений?

2. Решите уравнение:

3. Корнем каких из следующих уравнений является число 5:

1) 2х — 3 = 7, если х = 5, то:
2 • 5 — 3 = 7
10 — 3 = 7
7 = 7 — верно, значит число 5 является корнем уравнения 2х — 3 = 7.

2) х + 20 = 20 + х, если х = 5, то:
5 + 20 = 20 + 5
25 = 25 — верно, значит число 5 является корнем уравнения х + 20 = 20 + х.

3) 36 — 3х = 20, если х = 5, то:
36 — 3 • 5 = 20
36 — 15 = 20
21 ≠ 20 — неверно, значит число 5 не является корнем уравнения 36 — 3х = 20.

4) х • х • х + 25 = 150, если х = 5, то:
5 • 5 • 5 + 25 = 150
25 • 5 + 25 = 150
125 + 25 = 150
150 = 150 — верно, значит число 5 является корнем уравнения х • х • х + 25 = 150.

5) 0 • х = 10, если х = 5, то:
0 • 5 = 10
0 = 10 — неверно, значит число 5 не является корнем уравнения 0 • х = 10.

6) х + 12 = 22 — х, если х = 5, то:
5 + 12 = 22 — 5
17 = 17 — верно, значит число 5 является корнем уравнения 36 — 3х = 20.

Ответ: число 5 является корнем уравнений № 1, 2, 4, 6.

4. У Пети и Миши было поровну конфет. Петя отдал Мише 8 конфет. На сколько конфет у Миши стало больше, чем у Пети?

Пусть изначально у Пети и у Миши было по х конфет. Тогда после обмена стало:

Сравним, на сколько конфет у Миши стало больше, чем у Пети:

8 + 8 = 16 (конфет) — у Миши больше, чем у Пети.

Ответ: на 16 конфет.

Упражнения

281. Как можно обозначить угол, изображённый на рисунке 73?

Данный угол можно обозначить как: ∠K, ∠MKN, ∠NKM.

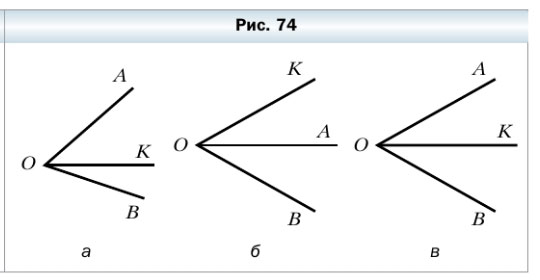
282. На каком из рисунков 74, а, б, в луч ОК является биссектрисой угла АОВ?

Луч ОК является биссектрисой угла АОВ на рисунке 74 б.

283. Назовите все углы, изображённые на рисунке 75.

На рисунке изображено 3 угла:

284. Запишите все углы, изображённые на рисунке 76.

На рисунке изображено 3 угла:

285. Какие из лучей, изображённых на рисунке 77, пересекают сторону угла ВОС?

Сторону угла ВОС пересекают лучи AK, ST.

286. Какие из лучей, изображённых на рисунке 78, пересекают сторону угла ВОС?

Сторону угла ВОС пересекают лучи RP, FE.

287. Начертите ∠MNE и проведите лучи NA и NC между его сторонами. Запишите все образовавшиеся углы.

На рисунке образовалось 6 углов:

288. На рисунке 79 ∠ABE = ∠ СВF. Есть ли ещё на этом рисунке равные углы?

На рисунке изображены следующие равные углы:

289. На рисунке 80 ∠AOB = ∠DOE, ∠BOC = ∠COD. Есть ли ещё на этом рисунке равные углы?

На рисунке изображены следующие равные углы:

290. На рисунке 81 углы FOK и МОЕ равны. Какие ещё углы, изображённые на этом рисунке, равны?

На рисунке изображены следующие равные углы:

Упражнения для повторения

291. Составьте числовое выражение и найдите его значение:

292. Решите уравнение:

293. На ХХП зимних Олимпийских играх, состоявшихся в 2014 г. в городе Сочи, олимпийская сборная России завоевала 33 медали. Наши спортсмены получили 24 золотых и серебряных медали, а золотых и бронзовых — 22. Сколько медалей каждого вида завоевала на этой Олимпиаде наша сборная?

1) 33 — 22 = 11 (шт.) — медалей — серебряные.

2) 24 — 11 = 13 (шт.) — медалей — золотые.

3) 22 — 13 = 9 (шт.) — медалей — бронзовые.

Ответ: 13 золотых медалей, 11 серебряных медалей и 9 бронзовых медалей.

294. Учащиеся пятых классов ехали на двух автобусах на экскурсию. Когда из одного автобуса, в котором было 42 учащихся, восемь учащихся перешли во второй автобус, то в обоих автобусах учащихся стало поровну. Сколько учащихся было во втором автобусе сначала?

Пусть во втором автобусе сначала было х учащихся. Тогда, после того перешло 8 учащихся из первого автобуса, во втором автобусе стало (х + 8) учащихся.

Мы знаем, что в первом автобусе сначала было 42 учащихся, а после перехода осталось (42 — 8) учащихся — столько же, сколько стало во втором автобусе после перехода.

х + 8 = 42 — 8
х + 8 = 34
х = 34 — 8
х = 26

Значит сначала в первом автобусе было 26 учащихся.

Задача от мудрой совы

295. На озере начали распускаться кувшинки. Каждый день количество кувшинок возрастало вдвое. На двадцатый день кувшинками заросла вся поверхность озера. На какой день половина озера была покрыта кувшинками?

Мы знаем, что каждый день количество кувшинок становилось вдвое больше (удваивалось), значит в предыдущий день в озере была половина кувшинок, но сравнению в последующим днём. То есть если на 20-й день озеро полностью заросло кувшинками, то половина от этого числа была в предыдущий день — 19-й.

Источник