частица в сферически симметричном поле
Частица в сферически симметричном поле
где, в отличие от (1.32), вместо V(r‘) стоит V(r’) и поэтому она тоже зависит лишь от r и угла θr между k и r, но не зависит от азимутального угла. Представим 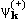
Однако, имея дело с задачей рассеяния, где более тонко стоит вопрос о дополнительных условиях к решению волнового уравнения, удобно наряду с дифференциальным уравнением (3.3) построить также и интегральное уравнение для функции R^(r), соответствующее интегральному уравнению (3.1).
Для этого подставим (3.2) в (3.1), разложим по парциальным волнам плоскую волну [1, с. 271]:
где jℓ(kr) − сферическая функция Бесселя, и, умножив правую и левую части уравнения на Pℓ(cosθr), воспользуемся свойством ортонормированности полиномов Лежандра:
Воспользуемся вьфажением (1.21) для функции Грина, а также известным в теории специальных функций разложением [3]:
где r − большее из значений r и r‘, 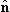
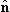
получаем интегральное уравнение для радиальных функций Rℓ(r) в окончательном виде:
функция Грина для ℓ-й парциальной волны свободной частицы.
Рассмотрим асимптотику радиальных функций Rℓ(r) при больших r. Для этого нам понадобятся асимптотические выражения сферических функций Бесселя и Неймана, входящих в (3.10) и
(3.11) [1, с. 269]:
Подставляя их в (3.11), получаем
Здесь мы ограничились случаем потенциала конечного радиуса. Введем обозначение
и запишем с его помощью асимптотическое выражение (3.14) более компактно:
Подставляя это выражение в (3.2) и снова используя (3.4), получаем
Отсюда видно, что ƒℓ − это коэффициент разложения амплитуды рассеяния по полиномам Лежандра:
§ 3.2. Фазы рассеяния
Перестроим асимптотическое выражение (3.16), придав ему вид суперпозиции сходящейся и расходящейся сферических волн:
Условие (3.20) позволяет ввести для описания каждой парциальной амплитуды рассеяния ƒℓ(k), являющейся, вообще говоря, комплексной функцией энергии (импульса) частицы, одну вещественную функцию δℓ(k), называемую фазой рассеяния :
To же соотношение полезно записать и по-другому:
При каждом значении энергии (импульса) частицы фазы рассеяния δℓ полностью определяют асимптотический вид радиальной функции Rℓ(r) соответствующей парциальной волны. Подставляя (3.21) в (3.19), получаем
Как видно из (3.15), при «выключении» взаимодействия частицы с силовым центром (V→0) обращаются в нуль все парциальные амплитуды рассеяния ƒℓ, а вместе с ними, согласно (3.21), и все фазы δℓ. При этом асимптотическое выражение (3.23) превращается в асимптотику ℓ-й составляющей волновой функции свободной частицы:
Сравнение выражений (3.24) и (3.23), отличающихся фазовым сдвигом в аргументе синуса, позволяет лучше понять смысл термина «фаза рассеяния».
Выразив через фазы рассеяния δℓ парциальные амплитуды ƒℓ, мы можем, пользуясь соотношениями (3.18) и (1.41), выразить через них полную амплитуду рассеяния, дифференциальное сечение, а затем и полное сечение рассеяния:
(при получении последней формулы мы воспользовались свойством ортонормированности полиномов Лежандра (3.5)). Формула (3.26) показывает, что угловое распределение рассеянных частиц зависит от интерференции между парциальными волнами с разными значениями орбитального момента частицы. Однако в полном сечении рассеяния а после интегрирования по всем углам вьшета рассеянной частицы эффект интерференции пропадает.
Сравнение формул (3.25) и (3.27) позволяет установить интересное соотношение между мнимой частью амплитуды рассеяния вперёд и полным сечением рассеяния:
§ 3.3. Энергетическая зависимость фаз рассеяния при низких энергиях
Это и есть искомая зависимость фаз рассеяния от энергии (импульса) частиц при малых энергиях. Она носит универсальный характер и присуща рассеянию на любом потенциале конечного радиуса.
§ 3.4. Методы вычисления фаз рассеяния
Точное решение задачи рассеяния с целью вычисления фаз рассеяния возможно лишь для отдельных искусственно придуманных потенциалов. На практике, когда приходится иметь дело с реалистическими потенциалами, фазы рассеяния всегда вычисляются приближенно, что связано либо с использованием тех или иных физических аппроксимаций, либо с проведением численного счета. Мы познакомимся с методами и того и другого родов.
а) Метод решения радиального уравнения Шредингера
Перепишем уравнение (3.3) в виде
Здесь, как и при решении задачи о связанных состояниях частицы [1, с.114], функции uℓ(r) связаны с Rℓ(r) соотношением
и при малых r ведут себя согласно степенному закону:
Поведение uℓ(r) при асимптотически больших г получаем из (3.23):
В общем случае уравнение (3.34) интегрируется численно, начиная от r = 0; для «разгонки» численного интегрирования удобно использовать свойство (3.36). Мы не будем вдаваться в чисто вычислительные аспекты этой процедуры. Для нас важно, что задачей интегрирования является построение всего «профиля» функции uℓ(r) с выходом при r → ∞ на асимптотику (3.37); при этом должно быть соблюдено условие непрерывности функции uℓ(r) и ее первой производной u‘ℓ(r) во всей области 0 > 1, r > d. Если энергия частицы Е и размеры области взаимодействия d таковы, что условие kr >> 1 не выполняется, то асимптотическое поведение (3.37) начинается далеко за границей области взаимодействия (r >> d). В этом случае не рационально доводить численное интегрирование до асимптотически больших значений r >> d, поскольку уже при r > d частица движется свободно и уравнение (3.3) переходит в уравнение движения свободной частицы:
При Е > 0 его линейно независимыми решениями являются сферическая функция Бесселя jℓ(kr) и сферическая функция Неймана nℓ(kr), а общее решение уравнения (3.34) при r > d имеет вид
Вместо констант интегрирования Аℓ и Вℓ удобно выбрать две другие:
С учетом (3.12) и (3.13) отсюда видно, что общее решение (3.39) имеет требуемую асимптотику (3.37).
Таким образом, практическая задача интегрирования уравнения (3.34) заключается в том, чтобы, начиная с r = 0, выйти в область свободного движения частицы r > d и «сшить» волновую функцию, найденную для внутренней области, с функцией (3.41). Пусть 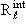
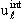
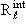
Исключая из (3.42) константу Cℓ (а вместе с ней и произвольно выбираемый при интегрировании уравнения (3.3) нормировочный множитель в 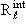
В качестве примера рассчитаем фазы рассеяния частицы на прямоугольной яме:
В этом случае для получения волновой функции Rℓ(r) во внутренней области не требуется численного интегрирования:
Отсюда находим логарифмическую производную (3.43):
а далее по формуле (3.44) и фазу рассеяния:
В качестве другого примера рассмотрим рассеяние частицы абсолютно твердой сферой. На поверхности такой сферы (r = d) «внешняя» волновая функция обращается в нуль:
Подставляя сюда (3.41), находим
В частности, при малых энергиях частицы отсюда получаем
б) Теория возмущений
Если V(r) мало, то радиальную функцию Rℓ(r), входящую в формулу (3.29) для фазы и удовлетворяющую уравнению (3.10), можно заменить во внутренней области (r ℓ (2ℓ + 1)jℓ(kr). Тогда получаем приближенное выражение для фазы:
а вместе с ним и для парциальной амплитуды рассеяния:
Таким образом, условие применимости теории возмущений для фаз − это малость фаз:
в) Метод фазовых функций
С точки зрения математики метод фазовых функций представляет собой особый способ решения радиального уравнения Шредингера (3.3), являющегося линейным дифференциальным уравнением второго порядка, или соответствующего ему интегрального уравнения (3.10). Он очень удобен для получения фаз рассеяния, так как по этому методу не требуется сначала вычислять в широкой области радиальные волновые функции задачи рассеяния и уже лишь потом, по их асимптотике, находить фазы. Сводя дело к решению нелинейного дифференциального уравнения первого порядка, метод фазовых функций очень удобен также с точки зрения выполнения численных расчетов на ЭВМ. Ниже мы изложим лишь основную идею этого метода.
Будем отправляться от интегрального уравнения (3.10), куда подставим функции Грина 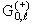
Используя (3.29), легко показать, что отношение этих функций при асимптотически больших г дает фазу рассеяния:
Фазовой функцией называется функция δℓ(r), определенная соотношением
Как видно из (3.64), ее предел при r → ∞ есть фаза рассеяния:
Легко убедиться путем непосредственной подстановки выражения (3.65), что фазовая функция δℓ(r) удовлетворяет при всех r уравнению
которое надо решать с дополнительным условием:
Конечно, для получения предельного значения δℓ(∞) достаточно интегрировать уравнение (3.67) от нуля до границы области взаимодействия. Это хорошо видно также, если уравнению (3.67) придать вид интегрального уравнения:
Уравнения (3.68) и (3.69) раскрывают физический смысл функции δℓ(r): фазовая функция δℓ(r), соответствующая заданному потенциалу V(r), − это фаза рассеяния частицы потенциалом, который «обрезан» в точке r, а на меньших расстояниях совпадает с V(r).
Упражнения
3.1. Найти связь между функцией Грина 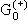
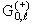
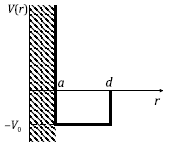 |
3.2. Получить общую формулу для фаз рассеяния δℓ частицы потенциальной ямой глубины V0 радиуса d с бесконечной отталкивающей серединой paдиуса а в центре ямы (см. рис.).
3.3. Вычислить борновскую фазу s-волны 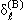
Важная проблема в квантовая механика это частица в сферически симметричный потенциал, т.е. потенциал, который зависит только от расстояния между частицей и определенной центральной точкой. В частности, если рассматриваемая частица является электроном, а потенциал получается из Закон Кулона, то задача может быть использована для описания водородоподобного (одноэлектронного) атома (или иона).
В общем случае динамика частицы в сферически-симметричном потенциале определяется Гамильтониан следующего вида:
ЧАС ^ = п ^ 2 2 м 0 + V ( р ) < displaystyle < hat > ^ <2>> <2m_ <0>>> + V (r)> в которой сферические полярные углы θ и φ представляют собой холодность и азимутальный угол соответственно. Последние два фактора ψ часто группируются как сферические гармоники, так что собственные функции принимают вид Оператор кинетической энергии в сферические полярные координаты является Подставив это в Уравнение Шредингера получаем одномерное уравнение на собственные значения, которое в точности является одномерным уравнением Шредингера с эффективным потенциалом, заданным формулой Возникают пять особых случаев, имеющих особое значение: Мы описываем решения в этих случаях, которые следует сравнить с их аналогами в декартовы координаты, ср. частица в коробке. Эта статья в значительной степени опирается на Функции Бесселя и Полиномы Лагерра. Давайте теперь рассмотрим V(р) = 0 (если V 0 < displaystyle V_ <0>> уравнение становится уравнением Бесселя для J определяется J ( ρ ) = d е ж ρ р ( р ) < Displaystyle J ( rho) < stackrel < mathrm куда k = d е ж 2 м 0 E / ℏ < Displaystyle к < stackrel < mathrm Сначала мы рассмотрим связанные состояния, то есть состояния, при которых частица отображается в основном внутри бокса (ограниченные состояния). У тех есть энергия E меньше потенциала вне сферы, т. е. имеют отрицательную энергию, и мы увидим, что существует дискретное количество таких состояний, которое мы сравним с положительной энергией с непрерывным спектром, описывающим рассеяние на сфере (несвязанных состояний ). Также стоит отметить, что в отличие от кулоновского потенциала, имеющего бесконечное количество дискретных связанных состояний, сферическая квадратная яма имеет только конечное (если есть) число из-за своего конечного диапазона (если он имеет конечную глубину). Первое ограничение связано с тем, что Neumann N и Ганкель ЧАС функции особые в начале координат. Физический аргумент, что ψ должен быть определен везде выбран Функция Бесселя первого рода J над другими возможностями в случае вакуума. По этой же причине решение внутри сферы будет таким: Связанные состояния вносят новизну по сравнению с вакуумным случаем, который E теперь отрицательный (в вакууме он должен был быть положительным). Это, наряду с третьим ограничением, выбирает функцию Ганкеля первого рода как единственное сходящееся решение на бесконечности (сингулярность в начале координат этих функций не имеет значения, так как теперь мы находимся вне сферы): Второе ограничение на непрерывность ψ при р = р 0 < displaystyle r = r_ <0>> В Эта статья показано, что N-мерный изотропный гармонический осциллятор имеет энергии Константа нормализации Nнл является, Сначала мы преобразуем радиальное уравнение несколькими последовательными подстановками в обобщенное дифференциальное уравнение Лагерра, которое имеет известные решения: обобщенные функции Лагерра. Затем мы нормируем обобщенные функции Лагерра на единицу. Это нормализация с обычным элементом объема. р 2 dр. Сначала мы шкала радиальная координата а затем уравнение принимает вид Рассмотрение предельного поведения v(у) в начале координат и на бесконечности предлагает следующую замену v(у), Эта замена преобразует дифференциальное уравнение к виду Выражение в квадратных скобках умножения ж(у) превращается в дифференциальное уравнение, характеризующее обобщенное Уравнение Лагерра (смотрите также Уравнение Куммера): Условие нормировки радиальной волновой функции: Используя свойства ортогональности обобщенных полиномов Лагерра это уравнение упрощается до Следовательно константа нормализации можно выразить как Другие формы константы нормализации могут быть получены с помощью свойства гамма-функции, отмечая, что п и л имеют одинаковую четность. Это означает, что п + л всегда чётно, так что гамма-функция становится где мы использовали определение двойной факториал. Следовательно, нормировочная константа также определяется выражением Масса м0, введенное выше, является уменьшенная масса системы. Поскольку масса электрона примерно в 1836 раз меньше массы легчайшего ядра (протона), величина м0 очень близка к массе электрона ме для всех водородных атомов. В оставшейся части статьи мы делаем приближение м0 = ме. С ме будут явным образом присутствовать в формулах, при необходимости это приближение будет легко исправить. Чтобы упростить уравнение Шредингера, мы вводим следующие константы, которые определяют атомная единица энергии и длины соответственно, Существуют два класса решений этого уравнения: (i) W отрицательна, соответствующие собственные функции интегрируемы с квадратом, а значения W квантованы (дискретный спектр). (ii) W неотрицательно. Каждое действительное неотрицательное значение W физически разрешено (непрерывный спектр), соответствующие собственные функции неквадратично интегрируемы. В оставшейся части статьи будут рассмотрены только решения класса (i). Волновые функции известны как связанные состояния, в отличие от решений класса (ii), известных как состояния рассеяния. которые обобщенные полиномы Лагерра порядка k. Мы возьмем соглашение для обобщенных многочленов Лагерра Абрамовица и Стегуна. [2] Обратите внимание, что полиномы Лагерра, приведенные во многих учебниках по квантовой механике, например в книге Мессии, [1] являются таковыми Абрамовица и Стегуна, умноженными на коэффициент (2l + 1 + k)! Данное определение в этой статье Википедии совпадает с таковой Абрамовица и Стегуна. с константой нормировки что принадлежит энергии При вычислении постоянной нормировки использовался интеграл [3] Важная проблема в квантовая механика это частица в сферически симметричный потенциал, т.е. потенциал, который зависит только от расстояния между частицей и определенной центральной точкой. В частности, если рассматриваемая частица является электроном, а потенциал получается из Закон Кулона, то задача может быть использована для описания водородоподобного (одноэлектронного) атома (или иона). В общем случае динамика частицы в сферически-симметричном потенциале определяется Гамильтониан следующего вида: ЧАС ^ = п ^ 2 2 м 0 + V ( р ) < displaystyle < hat > ^ <2>> <2m_ <0>>> + V (r)> в которой сферические полярные углы θ и φ представляют собой холодность и азимутальный угол соответственно. Последние два фактора ψ часто группируются как сферические гармоники, так что собственные функции принимают вид Оператор кинетической энергии в сферические полярные координаты является Подставив это в Уравнение Шредингера получаем одномерное уравнение на собственные значения, которое в точности является одномерным уравнением Шредингера с эффективным потенциалом, заданным формулой Возникают пять особых случаев, имеющих особое значение: Мы описываем решения в этих случаях, которые следует сравнить с их аналогами в декартовы координаты, ср. частица в коробке. Эта статья в значительной степени опирается на Функции Бесселя и Полиномы Лагерра. Давайте теперь рассмотрим V(р) = 0 (если V 0 < displaystyle V_ <0>> уравнение становится уравнением Бесселя для J определяется J ( ρ ) = d е ж ρ р ( р ) < Displaystyle J ( rho) < stackrel < mathrm куда k = d е ж 2 м 0 E / ℏ < Displaystyle к < stackrel < mathrm Сначала мы рассмотрим связанные состояния, то есть состояния, при которых частица отображается в основном внутри бокса (ограниченные состояния). У тех есть энергия E меньше потенциала вне сферы, т. е. имеют отрицательную энергию, и мы увидим, что существует дискретное количество таких состояний, которое мы сравним с положительной энергией с непрерывным спектром, описывающим рассеяние на сфере (несвязанных состояний ). Также стоит отметить, что в отличие от кулоновского потенциала, имеющего бесконечное количество дискретных связанных состояний, сферическая квадратная яма имеет только конечное (если есть) число из-за своего конечного диапазона (если он имеет конечную глубину). Первое ограничение связано с тем, что Neumann N и Ганкель ЧАС функции особые в начале координат. Физический аргумент, что ψ должен быть определен везде выбран Функция Бесселя первого рода J над другими возможностями в случае вакуума. По этой же причине решение внутри сферы будет таким: Связанные состояния вносят новизну по сравнению с вакуумным случаем, который E теперь отрицательный (в вакууме он должен был быть положительным). Это, наряду с третьим ограничением, выбирает функцию Ганкеля первого рода как единственное сходящееся решение на бесконечности (сингулярность в начале координат этих функций не имеет значения, так как теперь мы находимся вне сферы): Второе ограничение на непрерывность ψ при р = р 0 < displaystyle r = r_ <0>> В Эта статья показано, что N-мерный изотропный гармонический осциллятор имеет энергии Константа нормализации Nнл является, Сначала мы преобразуем радиальное уравнение несколькими последовательными подстановками в обобщенное дифференциальное уравнение Лагерра, которое имеет известные решения: обобщенные функции Лагерра. Затем мы нормируем обобщенные функции Лагерра на единицу. Это нормализация с обычным элементом объема. р 2 dр. Сначала мы шкала радиальная координата а затем уравнение принимает вид Рассмотрение предельного поведения v(у) в начале координат и на бесконечности предлагает следующую замену v(у), Эта замена преобразует дифференциальное уравнение к виду Выражение в квадратных скобках умножения ж(у) превращается в дифференциальное уравнение, характеризующее обобщенное Уравнение Лагерра (смотрите также Уравнение Куммера): Условие нормировки радиальной волновой функции: Используя свойства ортогональности обобщенных полиномов Лагерра это уравнение упрощается до Следовательно константа нормализации можно выразить как Другие формы константы нормализации могут быть получены с помощью свойства гамма-функции, отмечая, что п и л имеют одинаковую четность. Это означает, что п + л всегда чётно, так что гамма-функция становится где мы использовали определение двойной факториал. Следовательно, нормировочная константа также определяется выражением Масса м0, введенное выше, является уменьшенная масса системы. Поскольку масса электрона примерно в 1836 раз меньше массы легчайшего ядра (протона), величина м0 очень близка к массе электрона ме для всех водородных атомов. В оставшейся части статьи мы делаем приближение м0 = ме. С ме будут явным образом присутствовать в формулах, при необходимости это приближение будет легко исправить. Чтобы упростить уравнение Шредингера, мы вводим следующие константы, которые определяют атомная единица энергии и длины соответственно, Существуют два класса решений этого уравнения: (i) W отрицательна, соответствующие собственные функции интегрируемы с квадратом, а значения W квантованы (дискретный спектр). (ii) W неотрицательно. Каждое действительное неотрицательное значение W физически разрешено (непрерывный спектр), соответствующие собственные функции неквадратично интегрируемы. В оставшейся части статьи будут рассмотрены только решения класса (i). Волновые функции известны как связанные состояния, в отличие от решений класса (ii), известных как состояния рассеяния. которые обобщенные полиномы Лагерра порядка k. Мы возьмем соглашение для обобщенных многочленов Лагерра Абрамовица и Стегуна. [2] Обратите внимание, что полиномы Лагерра, приведенные во многих учебниках по квантовой механике, например в книге Мессии, [1] являются таковыми Абрамовица и Стегуна, умноженными на коэффициент (2l + 1 + k)! Данное определение в этой статье Википедии совпадает с таковой Абрамовица и Стегуна. с константой нормировки что принадлежит энергии При вычислении постоянной нормировки использовался интеграл [3]Содержание
Структура собственных функций
Вывод радиального уравнения.
Решения для интересующих потенциалов
Вакуумный чемодан






Сфера с конечным «квадратным» потенциалом

Сфера с бесконечным «квадратным» потенциалом
Трехмерный изотропный гармонический осциллятор
Вывод
Преобразование в полиномы Лагерра.
Восстановление нормированной радиальной волновой функции
Водородоподобные атомы
Содержание
Структура собственных функций
Вывод радиального уравнения.
Решения для интересующих потенциалов
Вакуумный чемодан






Сфера с конечным «квадратным» потенциалом

Сфера с бесконечным «квадратным» потенциалом
Трехмерный изотропный гармонический осциллятор
Вывод
Преобразование в полиномы Лагерра.
Восстановление нормированной радиальной волновой функции
Водородоподобные атомы

