решить систему уравнений в поле

Решить систему в поле вычетов

решите систему уравнений:

в поле вычетов по модулю 5 и по модулю 7. (если нетрудно прокомментируйте чтоб можно было разобраться)

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Решить уравнение № 2 x^2+5x+1=0 в поле вычетов по модулю 11
Решить уравнение в поле вычетов по модулю 11 x^2+5x+1=0

Примитивный элемент в поле вычетов
Здравствуйте. Объясните, пожалуйста, как найти примитивный элемент в поле GF(2^3) или GF(5^3). С.

Решение

Решение

В поле вычетов все ненулевые элементы имеют обратные (по умножению):
.
Думаю понятно, что мы работаем не с числами, а с классами вычетов, поэтому правильно писать
, но для краткости пишем без обозначения классов. Исходя из данных равенств, приводим расширенную матрицу к ступенчатому виду:
1 2 3 | 1
0 0 1 | 1
0 0 0 | 1

Так как ранг расширенной матрицы больше ранга матрицы системы, то по теореме Кронеккера-Капелли в поле решения нет, то есть система несовместна.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Система уравнений в поле вычетов по модулю
Помогите решить систему уравнений: в поле вычетов по модулю 5 и по модулю 7.

Найти ответ в системе уравнений в поле вычетов по модулю 5
Найти ответ в системе уравнений в поле вычетов по модулю 5. 3×1+4×2=1 2×1+x2=2 По методу.

Поле Галуа. Решить систему
необходимо решить в GF(23) систему 2х+2у=3 х+2у=2

решить систему
помогите найти х,у решив систему u=x+y v=1\x+1\y

Источник

Решение системы уравнений в Microsoft Excel

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Варианты решений

Любое уравнение может считаться решенным только тогда, когда будут отысканы его корни. В программе Excel существует несколько вариантов поиска корней. Давайте рассмотрим каждый из них.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

Аргумент «Массив» — это, собственно, адрес исходной таблицы.

Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию», расположенную около строки формул.

Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций, нажав значок «Вставить функцию».

Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение

Вместо значения «X» подставляем адрес той ячейки, где расположено число 0, принятое нами за x.

Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x.

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1:

Таким образом, как и у функции МОБР, единственным аргументом выступает ссылка на обрабатываемую таблицу.

Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию».

Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter. К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.

После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter.

Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter.

Жмем привычное уже нам сочетание клавиш для применения формулы массива.

Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter.

Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Помимо этой статьи, на сайте еще 12277 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Источник

Решение систем уравнений в поле.

Подскажите как решаются системы уравнений в поле. Вот например такая:

Решение систем из 7 уравнений! Т.Т
Помогите решить, пожалуйста Т.Т Ничего не понимаю.

Решение однородных систем линейных уравнений
Всем доброго времени суток Помогите найти решения однородных систем линейных уравнений: или.

Решение систем линейных уравнений методом Гаусса.
Решить системы линейных уравнений методом Гаусса. Если система совместна, найти ее общее и частное.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Решение систем линейных уравнений методом Гаусса
Кто то может раскрыть следующую тему, пожалуйса? Метод Гауса розв’язку систем лiiнйних рiвнянь.

Решение систем уравнений методом перебора значений неизвестных
По проекту есть такая задача, что приходится решать системы уравнений методом перебора, потому что.

Решение систем линейных уравнений методом Гаусса
Помогите решить x+2y+3z=8 4x+5y+6z=19 7x+8y. =1(Вместо троеточия получаеться 0)

Решение системы нелинейных уравнений 8 уравнений – 8 неизвестных переменных
Решаю систему нелинейных уравнений в символьном виде, решение выполняю с помощью математических.

Источник

Решение систем уравнений в среде Microsoft Excel

Тип урока: урок закрепления изученного материала и объяснения нового.

ХОД УРОКА

I. Организационная часть.

Здравствуйте! Все мы знаем, что одну и ту же информацию можно закодировать любым способом. Перед вами набор чисел. Известно, что каждому числу ставится в соответствие буква в русском алфавите. Расшифруйте эту информацию, кто быстрее!

Ответ: “Знание – сила!”

Молодцы! А знаете, кому принадлежит это выражение? (Если нет, то один ученик ищет ответ в Интернете. Остальные отвечают на вопросы: Для чего предназначена программа Excel? (Программа Excel предназначена для хранения и обработки данных, представленных в табличном виде) Что собой представляет документ в Excel? (Каждый документ в Excel представляет собой набор таблиц – рабочую книгу, которая состоит из одного или многих рабочих листов) Какая функция используется для подсчета суммы чисел? (Функция СУММ). Как определить адрес ячейки? (Excel вводит номера ячеек автоматически. Адрес ячейки составляется как объединение номеров столбца и строки без пробела между ними)

Выражение английского философа Френсиса Бэкона “Знание – сила!” и будет эпиграфом к нашему уроку. («Нравственные и политические очерки», 1597).

II. Повторение пройденного материала.

Мы уже знакомы с программой Microsoft Excel, умеем записывать арифметические выражения и различные формулы, находить значения арифметических выражений и построить графики функций. Чтобы проверить выполнение домашнего задания, предлагаю каждому пройти тестирование. (Приложение 1)

Хорошо, все справились и каждому поставим соответствующие оценки в журнал. А давайте устроим путешествие в математику и вспомним, что мы понимаем под понятием: “Решить систему уравнений”? (Найти такие значения х и у, которые будут удовлетворять и первое уравнение и второе). Какие способы существуют для решения систем уравнений (метод подстановки, метод сложения и графический способ). Сегодня мы с вами научимся решать системы уравнений, используя возможности электронных таблиц.

III. Объяснение нового.

Получены приближенные значения решений. Чем меньше шаг, тем точнее значение координат точек пересечения.

Запишем алгоритм решения систем уравнений графическим способом:

1. Преобразовать систему уравнений, если это необходимо.

2. Задать начальные значения для Х.

3. Найти значение первой функции при заданных Х.

4. Найти значение второй функции при тех же Х.

5. Выделить блок с данными и построить графики функций, используя точечный тип диаграммы.

7. Для нахождения координат точек пересечения с заданной точностью построить новый график на том отрезке, где находится решение, с шагом, равным значению точности.

Б. Решить систему уравнений . Занесем в электронную таблицу исходные данные и расчетные формулы следующим образом:.

Для решения системы уравнений воспользуемся надстройкой Поиск решения, которая запускается через Сервис (-Надстройки) и заполним диалоговое окно следующим образом:

При нажатии на кнопку Выполнить происходит решение системы уравнений и в ячейках B3 и B4 высвечивается результат.

Запишем примерный алгоритм решения системы уравнений, используя Поиск решения

1. Преобразовать систему уравнений, если это необходимо

2. Записать исходные данные (в ячейку А1 ввести текст “Решите уравнение”, в ячейку В1 записать первое уравнение, в ячейку В2 второе уравнение, в ячейку А3 ввести текст “Х=”, в ячейку А4 “Y=”, в ячейку А5 “уравнение 1”, в ячейку А6 “уравнение 2”. В ячейке B3 хотим получить значение Х, в ячейке В4 – значение Y, их оставляем пустыми.

3. В ячейку В5 переписать уравнение 1, используя правило записи арифметических выражений, следующим образом: в левой части вместо Х указывать ячейку В3, вместо Y ячейку В4, правую часть отбросить. Таким же образом переписать левую часть второго уравнения в ячейку В6.

4. Выбрать команду Сервис – Поиск решения.

6. В поле “изменяя ячейки” указать ячейки, в которых хотим увидеть ответ (В3 и В4)

8. Решить систему уравнений, щелкнув кнопкой Выполнить

IV. Практическая работа на компьютере.

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

А. Решите систему уравнений графическим способом

Б. Решите систему уравнения, воспользовавшись командой Поиск решения:

V. Подведение итогов.

Повторить алгоритмы решения систем уравнений

Выставить оценки за тестирование в журнал

VI. Домашнее задание.

Решить рациональным способом системы уравнений:

;

Источник

Вычисления в полях вычетов

Рассмотрим некоторые особенности вычислений в полях вычетов. Найдем, например, определитель 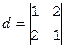, элементы которого суть вычеты из поля
(Z₃, +₃, ×₃). Если действовать «по науке», надо писать

Можно, однако, поступить проще. Будем считать элементы определителя обычными целыми числами из кольца Z, тогда d=1×1–2×2= –3.

Как найти для целого числа из Z соответствующий вычет из Z_n? Для этого надо к числу прибавить (или отнять от него) величину, кратную n, чтобы результат принадлежал множеству вычетов Z_n=<0,1,¼,n–1>. В данном случае прибавим 3 и получим –3+3=0 – тот же результат.

Рассмотрим решение системы линейных уравнений над полем вычетов.

Пример. Решим над тремя полями: Q, Z₃, Z₅ систему уравнений A×X=B, где . т.е.

Заметим, что коэффициенты системы (0, 1 и 2), включая свободные члены, можно рассматривать не только как числа (т.е. элементы поля Q), но и как элементы интересующих нас конечных полей Z₃ и Z₅. В противном случае постановку задачи пришлось бы как-то изменять.

Решать систему будем по правилу Крамера. Вычислим над полем Q четыре опре­делителя:

.

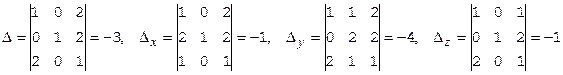
Значения неизвестных найдем по формулам Крамера: .

Приведем значения определителей в поле вычетов Z₃=<0,1,2>, получим: D=0, D_x=2, D_y=2, D_z=2. Видим, что над этим полем система несовместна.

Приведем значения определителей в поле вычетов Z₅=<0,1,2,3,4>: D=2, D_x=4, D_y=1, D_z=4. Значения неизвестных снова найдем по формулам Крамера: . Как понимать найденное значение неизвестной ? Дробь не является элементом поля Z₅, поэтому ее надо рассматривать как выражение, которое необходимо вычислить согласно правилам действий в этом поле: (поскольку произведение 2×3=6, а 6 в поле Z₅ переходит в 1). Итак, решение системы уравнений над полем Z₅ таково: x=2, y=3, z=2.

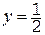
Сделаем проверку (символом Þ обозна­чен переход от целых чисел к вычетам по модулю 5). Первое уравнение: 1×2+2×2=6 Þ 1, второе уравнение: 1×3+2×2=7 Þ 2, третье уравнение: 2×2+1×2=6 Þ 1. Видим, что найден­ные значения вычетов удовлетворяют сис­теме уравнений над полем Z₅.

Решим ту же систему над полем Z₃ методом Гаусса. Составим расширенную матрицу: . Если бы мы решали систему над полем рациональных чисел Q, то первым шагом выполнили бы операцию (3)–2×(1). В поле Z₃ коэффициенту –2 соответствует вычет 1, поэтому выполним операцию (3)+1×(1). В 1-ом столбце имеем 2+1×1=3Þ0, во 2-ом столбце сохранится 0, в третьем столбце 1+1×2=3Þ0, в столбце свободных членов 1+1×1=2, так что . В алгебраической форме 3-е уравнение этой системы имеет вид 0×x+0×y+0×z=2. Очевидно, что оно не имеет решения, поэтому система над полем Z₃ несовместна.

Найдем решение той же системы над полем Z₅ методом Гаусса. Вместо операции (3)–2×(1), с которой начинается решение этой системы над полем рациональных чисел Q, выполним операцию (3)+3×(1), поскольку в поле Z₅ коэффициенту –2 соответствует вычет 3. В 1-ом столбце получим 2+3×1=5Þ0, во 2-ом столбце сохранится 0, в третьем, в 3-ем столбце имеем 1+3×2=7Þ2, в столбце свободных членов 1+3×1=4. Таким образом, получим . 3-ю строку этой матрицы можно сократить (разделить) на 2: .

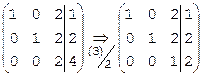
Теперь выполним операции (1)+3×(3) и (2)+3×(3) – в 1-й и во 2-й строках 3-го столбца получится 2+3×1=5Þ0, остальные элементы этих строк сохраняться: .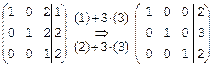

Видим, что получилось решение, ранее найденное по правилу Крамера: x=2, y=3, z=2.

Источник