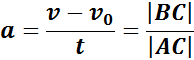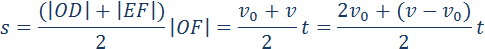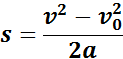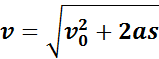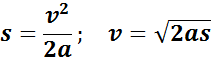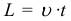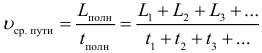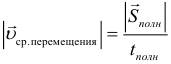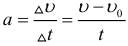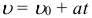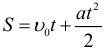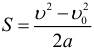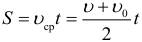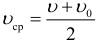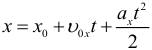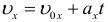Прямолинейное равноускоренное движение что это такое
Равноускоренное движение
В общем случае равноускоренным движением называют такое движение, при котором вектор ускорения 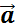
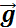
Таким образом, изучение равноускоренного движения сводится к изучению прямолинейного равноускоренного движения. В случае прямолинейного движения векторы скорости 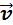
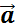
Проекции векторов скорости 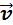
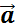
При равноускоренном прямолинейном движении скорость тела определяется формулой
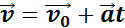
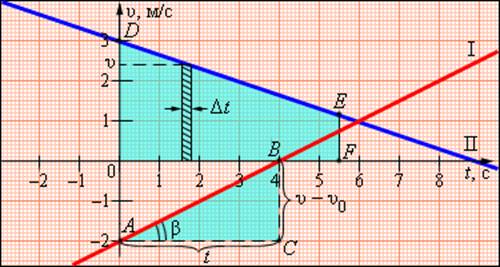
В этой формуле υ0 – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ (t) эта зависимость имеет вид прямой линии (рис. 1.4.2).
Графики скорости равноускоренного движения
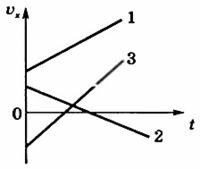
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис. 1.4.2 для графика I. Ускорение численно равно отношению сторон треугольника ABC:
Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.
Для графика II: υ0 = 3 м/с, a = –1/3 м/с 2
График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной полоски (рис. 1.4.2). Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, получим, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены для графика II на рис. 1.4.2. Время t принято равным 5,5 с.
Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:
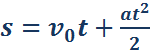
Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:
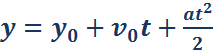
Это выражение называют законом равноускоренного движения.
При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ0 и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений, написанных выше, путем исключения из них времени t. Результат записывается в виде
Из этой формулы можно получить выражение для определения конечной скорости υ тела, если известны начальная скорость υ0, ускорение a и перемещение s:
Если начальная скорость υ0 равна нулю, эти формулы принимают вид
Следует еще раз обратить внимание на то, что входящие в формулы равноускоренного прямолинейного движения величины υ0, υ, s, a, y0 являются величинами алгебраическими. В зависимости от конкретного вида движения каждая из этих величин может принимать как положительные, так и отрицательные значения.
Равноускоренное движение.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.
Зависимость скорости от времени.
При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.
Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:
В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:
Формула для третьей компоненты скорости, если она необходима, выглядит аналогично.)
Закон движения.
Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:
Подставляем сюда выражение для скорости, даваемое формулой (3) :
Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:
Прямолинейное равноускоренное движение.
Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:
и подставим в формулу для перемещения:
После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:
Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.
Свободное падение.
Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.
Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.
Задача. Найти скорость приземления дождевой капли, если высота тучи км.
Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой
На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!
Задача. Тело брошено вертикально вверх со скоростью м/с. Найти его скорость через c.
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Задача. С балкона, находящегося на высоте м, бросили вертикально вверх камень со скоростью м/с. Через какое время камень упадёт на землю?
Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу
Горизонтальный бросок.
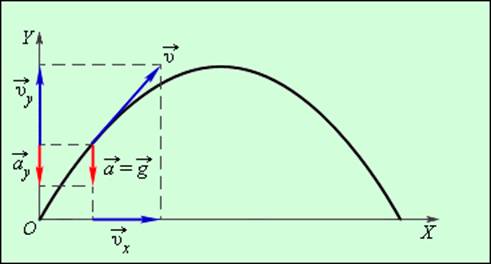
Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.
 |
| Рис. 1. Горизонтальный бросок |
Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:
Бросок под углом к горизонту.
Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.
 |
| Рис. 2. Бросок под углом к горизонту |
Начинаем с уравнений:
Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:
(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:
Учебники
Журнал «Квант»
Общие
Т. Равноускоренное движение
Равноускоренное прямолинейное движение
Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т. е. это движение с постоянным по модулю и направлению ускорением.
\vec a = \operatorname
По определению ускорения \(
Пусть в момент времени t0 = 0 скорость тела равна \(
\vec \upsilon_0\), в момент времени t — \(
\vec \upsilon\). Тогда за промежуток времени \(
\vec \upsilon = \vec \upsilon_0 + \vec a \cdot t\) — уравнение скорости.
\upsilon_x = \upsilon_ <0x>+ a_x \cdot t\].
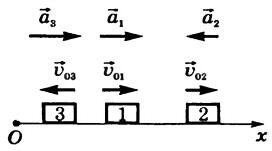
Эти зависимости кинематических величин от времени изобразим графически для трех тел (рис. 1).
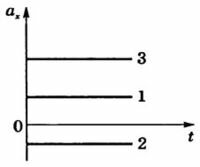
Графики ускорения ax = f(t) представлены на рисунке 2, а графики скорости υx = f(t) — на рисунке 3.
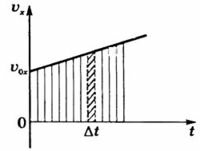
Для нахождения перемещения воспользуемся графиком скорости (рис. 4).
Для малого промежутка времени Δt изменением величины скорости можно пренебречь и скорость можно считать постоянной. Тогда перемещение за промежуток времени Δt будет равно площади узкой густо заштрихованной полоски. Мысленно разбив все время движения тела на малые промежутки времени и найдя перемещение за каждый отдельный промежуток времени, суммируем эти перемещения. Модуль проекции перемещения за промежуток времени \(
\upsilon_x = \upsilon_ <0x>+ a_x \cdot t\) в (1), получим:
\Delta r_x = \upsilon_ <0x>\cdot t + \frac
\Delta \vec r = \vec \upsilon_0 \cdot t + \frac<\vec a \cdot t^2><2>\) — уравнение перемещения в векторном виде.
x = x_0 + \Delta r_x\), имеем:
x = x_0 + \upsilon_ <0x>\cdot t + \frac
Исключая из уравнений скорости и перемещения время t, получим:
Сравнивая выражение (1) с формулой \(
\Delta r_x = \left\langle \upsilon \right\rangle_x \cdot t\), найдем:
\left\langle \upsilon \right\rangle_x = \frac <\upsilon_<0x>+ \upsilon_x><2>\) — проекция средней скорости при равноускоренном движении.
Графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения (рис. 5).
Равномерное и равноускоренное движение
В процессе такого перемещения скорость тела периодически изменяется, поэтому для описания данного процесса применяют понятия средней и мгновенной скоростей.
Мгновенная скорость – это скорость движения тела, которая фиксируется в конкретный момент времени в заданной точке пути. Другими словами, мгновенной скоростью \(v\) есть предел стремления средней скорости тела \(v_<ср>\) при бесконечно малом промежутке времени:
Известно, что предел отношения приращения функции к приращению аргумента, в случае стремления последнего к нулю, – это главная производная функции по аргументу.
Рассмотрим пример скатывания шарика по наклонной поверхности. При этом мы наблюдаем, что шарик движется неравномерно: расстояния, которые он проходит за одинаковые последовательные интервалы времени, постоянно увеличиваются. То есть, темп его движения постоянно растёт. Данное движение, как и скачивание любого предмета, является классикой прямолинейного равноускоренного перемещения.
Еще одним примером такого движения является перемещение транспорта, когда он разгоняется, а так же когда тормозит. То есть равноускоренным движением может считаться не только ускоренное, но и замедленное движение.
Дело в том, что понятие «ускорение» в физическом смысле более широкое, нежели мы привыкли использовать в ежедневной жизни. Слово ускорение в широком потреблении понимается как увеличение скорости, но физически под ускорением понимается передвижение тела с постоянным изменением скорости, при этом неважно увеличивается она или уменьшается.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Понятие прямолинейного равноускоренного движения достаточно широко используется при изучении законов механики.
Стоит отметить, что при влиянии постоянной силы тело будет перемещаться равноускорено.
Равномерное движение
Равномерное движение – это такое механическое перемещение тела, когда за равные промежутки времени оно преодолевает равные расстояния.
Для равномерного перемещения характерно постоянное значение скорости:
где \(v\) – скорость равномерного перемещения, м/с;
\(l\) – расстояние, преодоленное объектом, м;
\(δt\) – промежуток времени перемещения, с.
При равномерном перемещении скорость предмета остаётся равной на каждом промежутке пути.
Если перемещение тела не только равномерное, а также прямолинейное, то его путь равен модулю его перемещения. Значит, аналогично предыдущему выражению, определяем скорость равномерного прямолинейного перемещения:
где \(\overline
\(\overline\) – перемещение тела, м;
\(δt\) – промежуток времени перемещения, с.
Скорость равномерного прямолинейного перемещения является векторной величиной. То есть её направление также имеет значение, как и модуль.
Равноускоренное движение тела
При равноускоренном перемещении скорость постоянно изменяется. Если речь идет об убыстрении, скорость постоянно растет. То есть ускорение остаётся величиной постоянной, а темп постоянно растет.
Помимо равноускоренного движения еще выделяют равнозамедленное, где темп постоянно уменьшается с одинаковой быстротой.
Различают одномерное и многомерное ускорение. Первое происходит вдоль одной оси координат, а второе – в плоскости или в пространстве.
Не нашли что искали?
Просто напиши и мы поможем
Ускорение тела
Формулы равномерного движения для расчета ускорения могут применяться без учёта времени в разных плоскостях. Например, при расчёте свободного падения жестких тел, можно определять их местоположение. Это бывает полезно при различных геометрических расчётах.
Неравномерное перемещение тела, так же как и равноускоренное, характеризуется изменением скорости. Но в чём же тогда их отличие? При равноускоренном – скорость тела не просто изменяется, она равно ускоряется.
Понятие ускорения часто ассоциируют с ростом скорости. Поскольку скорость растет одинаково, говорят о равном возрастании скорости. Как же определить, скорость растет равномерно или нет? Для этого засекают время, оценивают приращение скорости за равные промежутки времени, если при этом приращение одинаково на каждом новом участке, передвижение считается равноускоренным.
Ускорение – это физическая величина, показывающая на сколько возрастает скорость.
Замедленным движением есть перемещение с уменьшающейся скоростью. Поскольку в физике любое перемещение с меняющейся скоростью называется ускоренным, то неважно разгоняется автомобиль либо тормозит, в любом случае он передвигается с ускорением.
Значит, ускорение описывает быстроту изменения скорости. Оно показывает на сколько меняется скорость за одну секунду. Чем больше величина ускорения, тем стремительнее тело набирает скорость либо сбрасывает её. Ускорение обозначается буквой a и определяется соотношением изменения скорости δv к промежутку времени δt, за которое оно осуществлено:
Равноускоренное прямолинейное движение



Раздел КИНЕМАТИКА.
Основные теоретические сведения
Система СИ
Основные единицы измерения величин в системе СИ таковы:
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
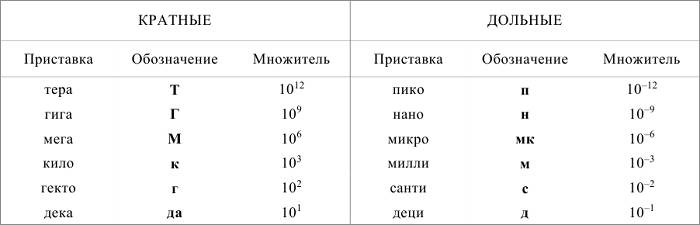
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
· При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
· И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела: