Прямая и плоскость имеют одну общую точку это значит что
Прямая и плоскость имеют одну общую точку это значит что
10 класс
Материалы к зачетной работе по теме
«Основные понятия и аксиомы стереометрии. Параллельность прямых и плоскостей»
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
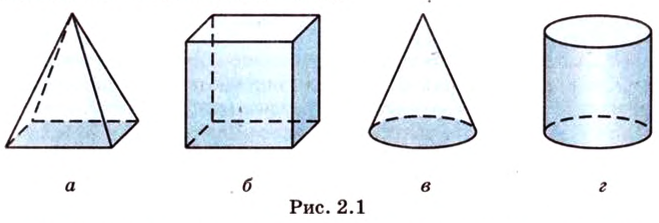
Простейшие фигуры в пространстве: точка, прямая, плоскость.

Аксиомы стереометрии и их следствия
Аксиома 2.
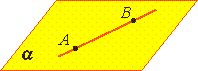
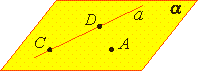
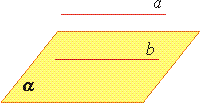
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
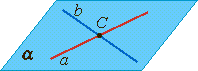
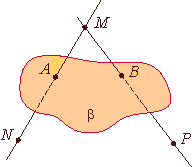
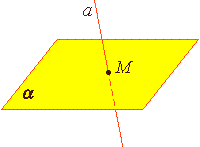
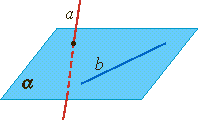
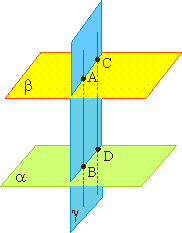
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.
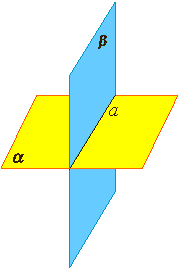
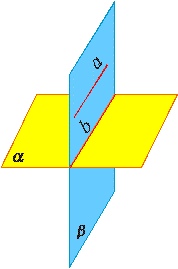
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Некоторые следствия из аксиом
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
Параллельные прямые в пространстве
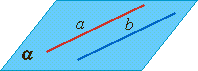
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема о трех прямых в пространстве.
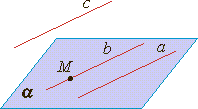
Если две прямые параллельны третьей прямой, то они параллельны (если a∥c и b∥c, то a∥b).
Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости
Теорема.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Теорема.
Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема.
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Взаимное расположение прямых в пространстве
 |  |  |
Признак параллельности двух плоскостей | 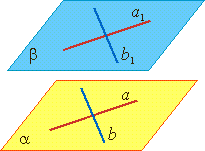 |
Свойства параллельных плоскостей
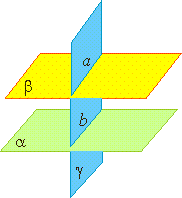
Вели α∥β и они пересекаются с γ, то а∥b.
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Лекция по теме: «Основные понятия стереометрии»
Первейшим гарантом непогрешимости математического мышления считается то, что исходным пунктом рассуждений и действий в этой науке служат аксиомы.
выдающийся физиолог, психолог
ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ
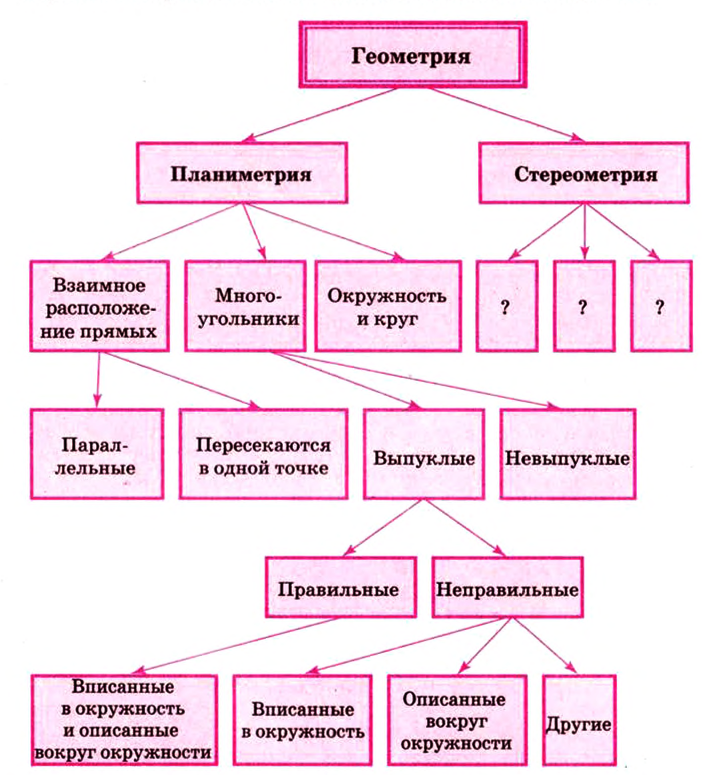
1 Структура курса геометрии
2 Определения и обозначения
3 Основные свойства плоскости
4 Взаимное расположение прямых и плоскостей в пространстве
1 Структура курса геометрии
Стереометрия — это раздел геометрии, в котором изучаются фигуры в пространстве. Она является второй составляющей геометрии и строится так же, как и планиметрия.
В стереометрии свойства геометрических фигур устанавливаются с помощью доказательства теорем (из греч. — рассматриваю), которые основываются на аксиомах (из греч. — считаю достойным, настаиваю, требую) — математических предложениях, принимаемых без доказательства
2 Определения и обозначения
Плоскость понимают также как множество точек.
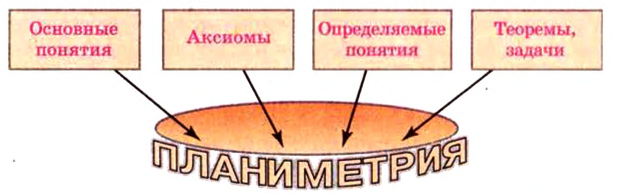
3 Основные свойства плоскости
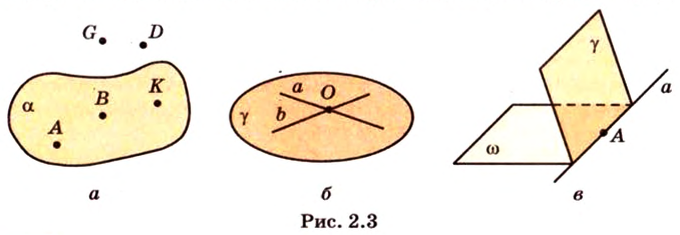
Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.
Система аксиом стереометрии состоит из двух групп. Первая из них включает все аксиомы планиметрии. Они выполняются в каждой плоскости пространства. Эти аксиомы вам известны из курса планиметрии. Здесь рассмотрим группу аксиом, выражающую основные свойства плоскостей в пространстве.
1 Через любые три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну
2 Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
3 Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.
Утверждение, истинность которого доказана и которое используют для доказательства других утверждений, называют теоремой. Простейшими теоремами являются следствия из аксиом стереометрии.
Теорема 1 Через прямую и точку, не принадлежащую ей, можно провести плоскость и притом только одну
Доказательство. Данная точка и две точки прямой составляют три точки, не лежащие на одной прямой. По аксиоме 1 через них проходит единственная плоскость. По аксиоме 3 данная прямая лежит в этой плоскости.
Теорема 2 Через две пересекающиеся прямые можно провести плоскость и притом только одну.
Доказательство. На каждой из прямых можно взять по одной необщей точке. Вместе с точкой пересечения прямых они образуют три точки, не лежащие на одной прямой. По аксиоме 1 через них проходит единственная плоскость. По аксиоме 3 обе прямые лежат в этой плоскости.
Теорема 3 Через две параллельные прямые можно провести плоскость и притом только одну.
Доказательство. По теореме 1 через одну из параллельных прямых и произвольную точку другой прямой можно провести плоскость, и притом только одну.
Если учесть вышеизложенное, то можно сделать вывод, что плоскость однозначно определяют:
1) три точки, не лежащие на одной прямой;
2) прямая и точка, не принадлежащая этой прямой;
3) две пересекающиеся прямые;
4) две параллельные прямые.
4 Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых в пространстве можно свести к следующим случаям.
1 Прямые пересекаются, тогда они лежат в одной плоскости.
2 Прямые параллельны — тогда они лежат в одной плоскости
3 Прямые не пересекаются и не параллельны — такие прямые называются скрещивающимися.
4 Прямые совпадают, если они имеют по крайней мере две общие точки
Возможны следующие варианты взаимного расположения прямой и плоскости в пространстве:
1) Прямая и плоскость имеют по крайней мере две общие точки. Тогда прямая лежит в плоскости, то есть прямая и плоскость имеют множество общих точек;
2) Прямая и плоскость имеют одну общую точку. Возможность такого размещения прямых и плоскостей обеспечивается тем, что вне плоскости являются точки пространства. Произвольная точка плоскости и точка вне плоскости определяют прямую, которая имеет с плоскостью одну общую точку, то есть пересекает ее.
3) Прямая и плоскость не имеют общих точек, то есть не пересекаются. Прямая и плоскость, которые не имеют общих точек, называются параллельными
Плоскости в пространстве могут принимать следующие положения друг относительно друга:
1 Две плоскости пересекаются по прямой — в этом случае они не имеют других общих точек вне этой прямой
2 Плоскости совпадают
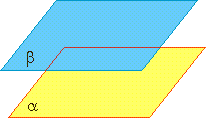
3 Если две разные плоскости не имеют общих точек, то они называются параллельными.
1 Какой раздел геометрии называется стереометрией?
2 Какие предложения называются аксиомами? Теоремами?
3 Сформулируйте аксиомы плоскости и следствия из них.
4 Назовите возможные варианты взаимного расположения прямых в пространстве.
5 Перечислите возможные варианты взаимного расположения прямой и плоскости в пространстве.
6 Приведите возможные варианты взаимного расположения плоскостей в пространстве.
Задачи, задания, вопросы
№3 Выберите для двух различных плоскостей и одинаковые по смыслу утверждения.
1) Плоскости и пересекаются;
2) плоскости и имеют лишь одну общую точку;
3) плоскости и имеют общую точку;
4) плоскости и имеют не больше двух общих точек;
5) плоскости и имеют общую прямую.
№5 Плоскости пересекаются. Определите количество общих прямых, которые они могут иметь.
№7 Выберите четыре утверждения, которые определяют единственность плоскости.
1) Любые две точки пространства;
2) любая прямая пространства и точка на ней;
3) любая прямая пространства и точка вне нее;
4) любые три прямых пространства;
5) любые три точки пространства;
6) любые две параллельные прямые;
7) любые две прямые;
8) любые две пересекающиеся прямые.
№13 Выберите правильное утверждение.
1) Через точку пространства, которая не лежит на прямой, можно провести множество прямых, которые параллельные данной;
2) две прямые, параллельные третьей, пересекаются в одной точке;
3) если две точки прямой принадлежат плоскости, то прямая пересекает плоскость;
4) через прямую и точку вне прямой можно провести две различные плоскости;
5) через точку пространства, не лежащую на плоскости, можно провести множество прямых, которые будут пересекать эту плоскость.
1) — единственная возможная плоскость, параллельная плоскости ;
2) — единственная возможная плоскость, пересекающая плоскость ;
3) — единственная возможная плоскость, параллельная плоскости ;
4) — единственная возможная плоскость, пересекающая плоскость ;
Математика: учебник для ссузов / Н. В. Богомолов, П. И. Самойленко. — 7-е изд., стереотип. — М.: Дрофа, 2010., стр. 320-323
Геометрия. 10-11 классы: учебник для учащихся общеобразоват. учреждений: базовый и профил. уровни / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. — 18-е изд., — М.: Просвещение, 2009, стр. 3-8.
Математика: підручник для 10 кл. загальноосвітніх навчальних закладів: рівень стандарту / О.М. Афанасьєва, Я.С. Бродський, О.Л. Павлов, А.К. Сліпенко. – Тернопіль: Навчальна книга – Богдан, 2010, стор. 127-133, 135-137
Лекция «Параллельность прямой и плоскости»
Параллельность прямой и плоскости.
Возможны три расположения прямой и плоскости:
1. прямая лежит в плоскости
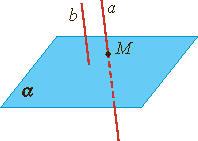
1. прямая и плоскость имеют только одну общую точку, т.е. пересекаются
1. прямая и плоскость не имеют ни одной общей точки
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Существует еще два утверждения, которые используются при решении задач:
1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.
Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10
Т.к. ACFE − параллелограмм, то АС=EF=10
Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.
MC
Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Лекция «Параллельность прямых в пространстве»
Презентация на тему «Решение задач по нахождению угла между прямой и плоскостью»
Презентация на тему «Решение задач на нахождение угола между прямыми в пространстве»
Внеклассное мероприятие по геометрии «Великие математики»
Тексты задач по окружности из сборника по подготовке к ОГЭ
Презентация урока подготовки к ОГЭ задача по теме «Окружность» 9 класс
Билеты для зачета по геометрии 8 класс
Презентация по геометрии на тему «Площади четырехугольников»(8 класс)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5426306 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Поставщики интернета для школ будут работать с российским оборудованием
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Российские юниоры завоевали 6 медалей на Международной научной олимпиаде
Время чтения: 2 минуты
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Липецкой области начинающие педагоги получат 120 тысяч рублей
Время чтения: 0 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Аксиомы стереометрии. Взаимное расположение двух прямых, прямой и плоскости, двух плоскостей в пространстве
Стереометрия – это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» – объемный, пространственный и «μετρεο» – измерять.
Плоскость
Представление о плоскости дает поверхность стола или стены, любая гладкая поверхность. Плоскость как геометрическую фигуру надо представлять себе как бесконечно неограниченную во все стороны поверхность.
Аксиомы стереометрии и их следствия


























 .
.
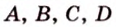 не лежат на одной плоскости. Докажите, что прямые
не лежат на одной плоскости. Докажите, что прямые 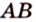 и
и 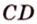 не пересекаются.
не пересекаются.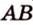 и
и 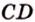 пересекаются (рис. 2.5).
пересекаются (рис. 2.5).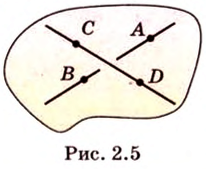
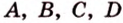 также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые
также принадлежат этой плоскости, что противоречит условию. Предположение неверно. Прямые 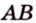 и
и 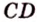 не пересекаются, что и требовалось доказать.
не пересекаются, что и требовалось доказать. 
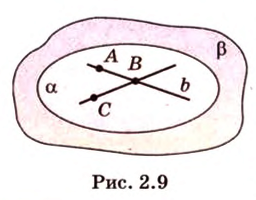
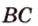 — данная прямая и
— данная прямая и 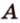 — точка, не принадлежащая ей (рис. 2.9). Через точки
— точка, не принадлежащая ей (рис. 2.9). Через точки 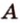 и
и 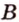 проведем прямую
проведем прямую 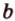 . Прямые
. Прямые 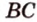 и
и 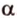 . Докажем, что она единственная, методом от противного.
. Докажем, что она единственная, методом от противного.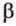 , которая содержит прямую
, которая содержит прямую 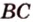 и точку
и точку 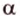 и
и 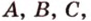 что противоречит условию. Предположение неверно. Плоскость
что противоречит условию. Предположение неверно. Плоскость 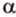 — единственная. Теорема доказана.
— единственная. Теорема доказана.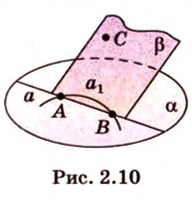
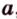 , плоскость
, плоскость 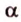 и точки А и В прямой
и точки А и В прямой 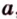 , принадлежащие
, принадлежащие 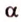 (рис. 2.10). Выберем точку С, которая не принадлежит прямой
(рис. 2.10). Выберем точку С, которая не принадлежит прямой 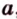 . Через точку С и прямую
. Через точку С и прямую 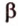 . Если
. Если 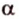 и
и 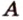 и
и 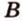 , то они пересекаются по прямой
, то они пересекаются по прямой 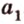 , содержащей эти точки. Поэтому через две точки
, содержащей эти точки. Поэтому через две точки 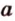 и
и 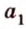 , что противоречит аксиоме принадлежности I2. Поэтому
, что противоречит аксиоме принадлежности I2. Поэтому 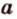 и
и 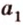 — совпадают. Однако поскольку
— совпадают. Однако поскольку 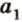 , принадлежит плоскости
, принадлежит плоскости 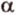 , то и прямая
, то и прямая 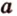 также принадлежит
также принадлежит 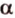 .
.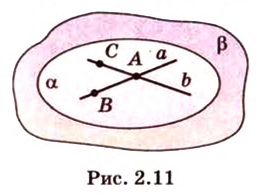
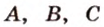 — заданные точки (рис. 2.11). Проведем через точки
— заданные точки (рис. 2.11). Проведем через точки 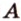 и
и 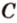 прямую
прямую 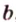 , а через точки
, а через точки 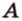 и
и 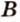 — прямую
— прямую 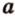 . Прямые
. Прямые 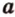 и
и 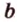 различны и имеют общую точку
различны и имеют общую точку 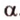 . Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость
. Докажем, что она единственная, методом от противного. Допустим, что существует другая плоскость 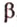 , содержащая точки
, содержащая точки 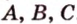 . Тогда, по теореме 2, прямые
. Тогда, по теореме 2, прямые 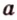 и
и 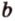 принадлежат плоскости
принадлежат плоскости 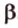 . Поэтому плоскости
. Поэтому плоскости 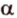 и
и 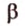 имеют две общие прямые
имеют две общие прямые 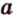 и
и 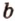 , которые пересекаются, что противоречит аксиоме II3. Итак, плоскость
, которые пересекаются, что противоречит аксиоме II3. Итак, плоскость 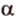 — единственная. Теорема доказана.
— единственная. Теорема доказана.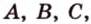 то в таком случае пользуются обозначением: (
то в таком случае пользуются обозначением: (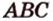 ). Читается: «плоскость, заданная точками
). Читается: «плоскость, заданная точками 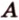 ,
, 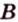 и
и 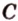 », или сокращенно «плоскость
», или сокращенно «плоскость 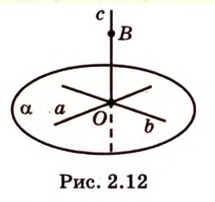
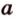 и
и 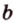 (рис. 2.12), которые имеют общую точку
(рис. 2.12), которые имеют общую точку 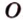 , можно провести плоскость
, можно провести плоскость 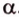 . Возьмем точку
. Возьмем точку 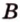 , которая не принадлежит
, которая не принадлежит 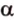 . Через точки
. Через точки 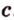 . Прямая
. Прямая 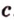 не лежит на плоскости
не лежит на плоскости 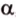 , так как если бы прямая
, так как если бы прямая 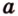 и
и  можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.
можно провести третью прямую, которая не лежит с ними в одной плоскости. Ответ. Можно.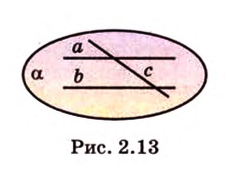
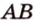 и
и 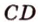 не лежат в одной плоскости, то прямые
не лежат в одной плоскости, то прямые 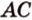 и
и 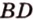 также не лежат в одной плоскости.
также не лежат в одной плоскости.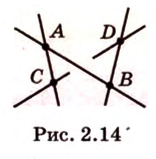
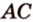 и
и 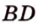 лежат в одной плоскости (рис. 2.14). Тогда точки
лежат в одной плоскости (рис. 2.14). Тогда точки 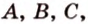
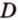 принадлежат этой плоскости, а следовательно, прямые
принадлежат этой плоскости, а следовательно, прямые 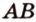 и
и 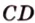 принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые
принадлежат этой плоскости, что противоречит условию. Предположение неверно, поэтому прямые 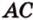 и
и 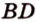 не принадлежат одной плоскости, что и требовалось доказать.
не принадлежат одной плоскости, что и требовалось доказать.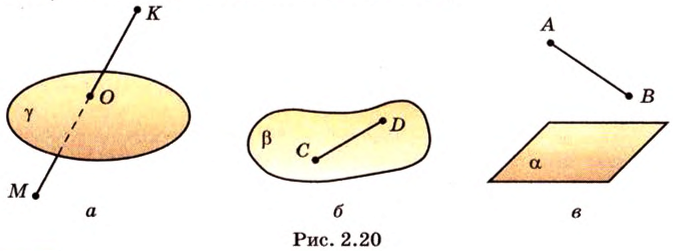
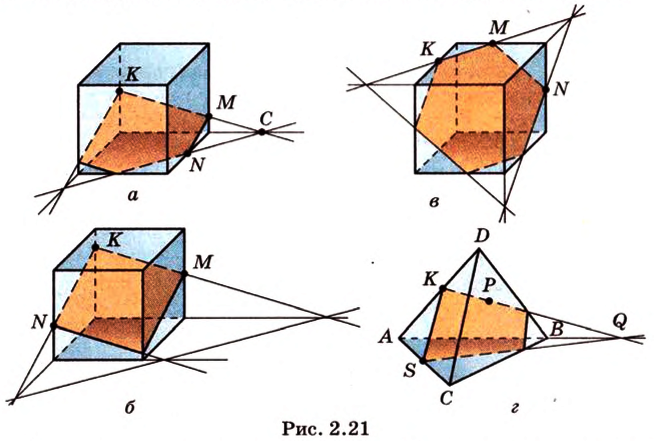
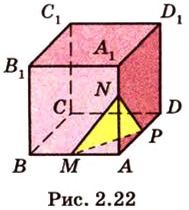
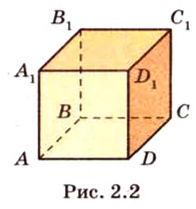
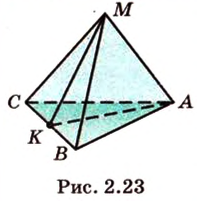
 — заданный куб (рис. 2.22). Выберем одну из вершин, например
— заданный куб (рис. 2.22). Выберем одну из вершин, например 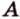 , являющуюся общей для трех ребер
, являющуюся общей для трех ребер 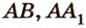 и
и 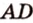 . Обозначим на этих ребрах точки
. Обозначим на этих ребрах точки 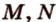 и
и 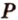 соответственно, являющиеся их серединами. Точки
соответственно, являющиеся их серединами. Точки 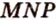 ). Точки
). Точки 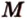 и
и 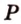 — общие точки плоскости сечения и грани
— общие точки плоскости сечения и грани 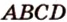 , поэтому
, поэтому 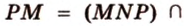
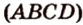 ,
, 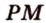 — сторона сечения.
— сторона сечения. 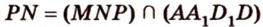 и
и 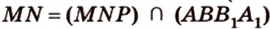 , поэтому
, поэтому 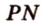 и
и 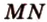 — две другие стороны сечения. Таким образом,
— две другие стороны сечения. Таким образом, 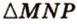 — искомое сечение.
— искомое сечение. плоскостью, которая проходит через ребро
плоскостью, которая проходит через ребро 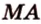 и середину ребра
и середину ребра 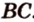 .
.
 плоскостью, проходящей через три точки, которые лежат соответственно на ребрах
плоскостью, проходящей через три точки, которые лежат соответственно на ребрах 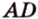 ,
, 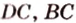 .
.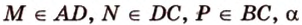 — секущая плоскость, проходящая через заданные точки
— секущая плоскость, проходящая через заданные точки 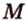 ,
, 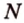 и
и 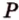 . Построим сечение, выполняя последовательно шаги:
. Построим сечение, выполняя последовательно шаги: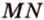 и
и 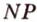 (рис. 2.24, а). Точка
(рис. 2.24, а). Точка 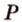 — общая точка двух плоскостей (
— общая точка двух плоскостей (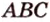 ) и (
) и (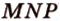 ). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку
). Такие плоскости (по аксиоме II4) пересекаются по прямой, проходящей через точку 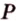 . Для построения такой прямой нужна вторая точка.
. Для построения такой прямой нужна вторая точка.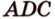 ) и (
) и (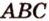 ) пересекаются по прямой
) пересекаются по прямой 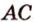 .
. 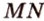 по условию не параллельна
по условию не параллельна 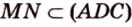 , поэтому
, поэтому 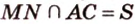 (рис. 2.24, б).
(рис. 2.24, б). 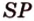 — линия пересечения плоскостей (
— линия пересечения плоскостей (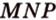 ) и (
) и (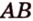 дает точку
дает точку 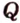 , которая является вершиной сечения. Таким образом, четырехугольник
, которая является вершиной сечения. Таким образом, четырехугольник 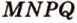 — искомое сечение (рис. 2.24, в).
— искомое сечение (рис. 2.24, в).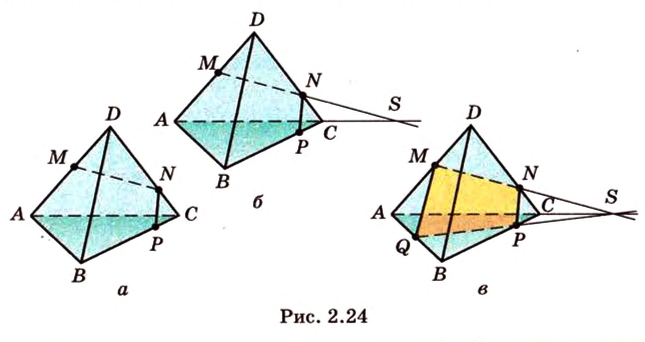
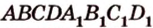 плоскостью, проходящей через середины
плоскостью, проходящей через середины 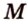 и
и 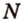 ребер
ребер 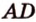 и
и 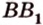 и точку
и точку 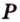 пересечения диагоналей грани (рис. 2.25, а).
пересечения диагоналей грани (рис. 2.25, а).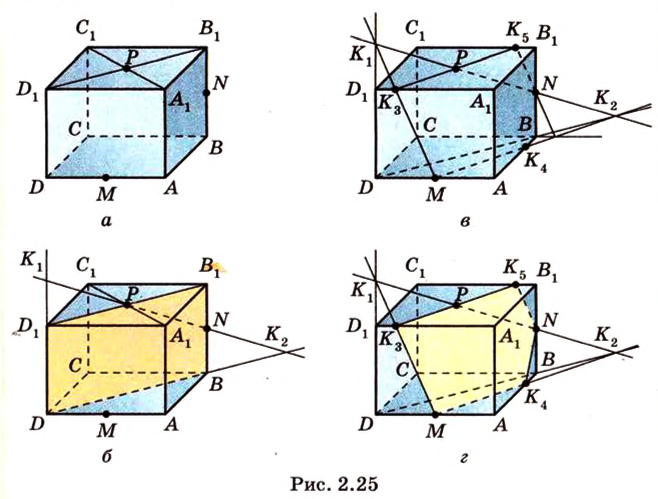
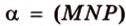 . Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.
. Выполним последовательно шаги, выполняя поиск фигуры, образованной плоскостью сечения.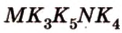 — искомое сечение (рис. 2.25, г).
— искомое сечение (рис. 2.25, г). 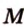 ,
, 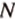 ,
, 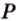 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам 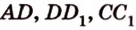 .
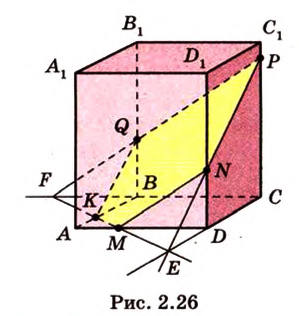
.
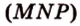 ) (рис. 2.26).
) (рис. 2.26).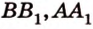 ,
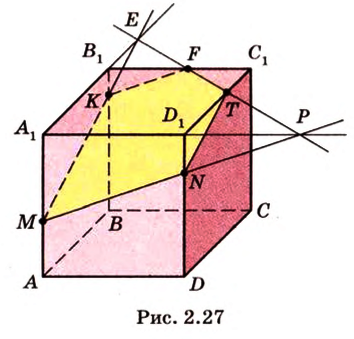
, 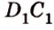 .
.
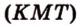 (рис. 2.27).
(рис. 2.27).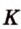 ,
, 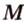 ,
, 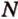 , которые принадлежат соответственно ребрам
, которые принадлежат соответственно ребрам 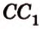 ,
,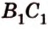 ,
,  .
.
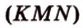 (рис. 2.28).
(рис. 2.28).