Проверить что точки служат вершинами трапеции

Проверить, что точки являются вершинами параллерограмма, трапеции или ромба

Проверить, не являются точки вершинами параллелограмма
есть А1(х1, у1), А2(x2,у2), А3(x3, у3), А4(х4, у4), не могу найти их длину Вот набросок.

Проверить что числа x, y являются координатами точки, лежащей в первой или третьей координатной четверти
Проверить истинность высказывания: «Данные числа x, y являются координатами точки, лежащей в первой.

Проверить являются ли заданные числа длинами сторон ромба, параллелограмма или четырёхугольника другого вида
Заданы 4 числа проверить являются ли они длинами сторон ромба, параллелограмма или четырёхугольника.

Решение

кричать очень даже не обязательно. здесь не слепые

1. Немного не понял какой ответ нужно получить (да/нет или вывести название фигуры)?
Проверять надо в таком порядке: трапеция, параллелограмм, ромб. Если точки не являются трапецией то остальное проверять не имеет смысла (любой ромб это параллелограмм, а любой параллелограмм это трапеция).
Проверять навернрое надо по признаку параллельностии противолежащих сторон, а у ромба еще и по длинне 2-х соседних сторон (остальные можно не проверять).

Вот собственно и ничего сложного.

На плоскости заданы три точки. Вычислите площадь треугольника, вершинами которого являются эти точки.
На плоскости заданы три точки. Вычислите площадь треугольника, вершинами которого являются эти.

Являются ли точки вершинами квадрата?
Заданы координаты трех точек на плоскости. Являются ли они вершинами квадрата? Если да, то найти.

Источник

Доказать что точки служат вершинами трапеции

1. Проверить, что точки служат вершинами трапеции. Найти длины её параллельных сторон.
A(3;-1;2)
B(1;2;-1)
C(-1;1;-3)
D(3;-5;3)

2. Доказать, что точки лежат на одной прямой, причём точка B расположена между A и С. Составить канонические уравнения этой прямой.
A(-3;-7;-5)
B(0;-1;-2)
C(2;3;0)
AB: `(x+3)/3=(y+7)/6=(z+5)/3`
BC: `x/2=(y+1)/4=(z+2)/2`
AC: `(x+3)/5=(y+7)/10=(z+5)/5`
Вообщем подставляю 3 точку в уравнение, получаю верное равенство => все 3 точки лежат на 1 прямой.
Как доказать, что B лежит между A и C?

Если вам понравился ответ, не забудьте нажать кнопку Спасибо, Отметить мой ответ, как лучший и поставить 5 звезд!

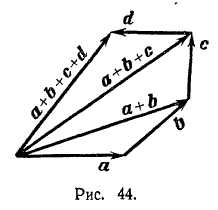
Суммой а + b двух векторов а и b называется вектор, который идет из начала вектора а в конец вектора b при условии, что вектор b приложен к концу вектора а (правило треугольника) Построение суммы а + b изображено на рис. 42.

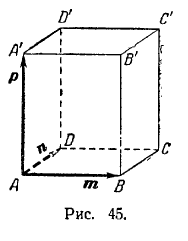
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 44, где изображено построение суммы четырех векторов а, b, с, d).

Произведением ом (или также aα) вектора а на число α называется вектор, модуль которого равен произведению модуля вектора а на модуль числа α; он параллелен вектору а или лежит с ним на одной прямой и направлен так же, как вектор а, если α — число положительное, и противоположно вектору а, если α — число отрицательное.

Сложение векторов и умножение вектора на число называются линейными операциями над векторами.

Имеют место следующие две основные теоремы о проекциях векторов:

1. Проекция суммы векторов на какую-нибудь ось равна сумме их проекций на эту же ось:

2. При умножении вектора на число его проекция умножается «а то же число:

Если а = (X; Y; Z), то для любого числа α

Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов

является пропорциональность их координат:

Тройка векторов i, j, k называется координатным базисом, если эти векторы удовлетворяют следующим условиям:

1) вектор i лежит на оси Ох, вектор i — на оси Оу, вектор k — на оси Oz;

2) каждый из векторов i, j, k направлен на своей оси в положительную сторону;

3) векторы i, j, k — единичные, т. е. |i| = 1, |j| = 1, |k| = 1

Каким бы ни был вектор а, он всегда может быть разложен по базису i, j, k, т. е. может быть представлен в виде:

коэффициенты этого разложения являются координатами вектора а (т. е. X, Y, Z суть проекции вектора а на координатные оси).

762. Даны: |а| = 13, |b| = 19 и |а + b| = 24. Вычислить |а — b|.

763. Даны: |а| = 11, |b| = 23 и |а — b| = 30. Определить |а + b|.

764. Векторы а и b взаимно перпендикулярны, причем |а| = 5 и |b| = 12. Определить |a + b| и |а — b|.

765. Векторы а и b образуют угол φ = 60°, причем |а| = 5 и |b| = 8. Определить |а + b| и |а — b|.

766. Векторы а и b образуют угол φ = 120°, причем |а| = 3 и |6| =5. Определить |a + b| и |а — b|.

771. Точка О является _центром тяжести треуголь-ника АБС. Доказать, что OA + OB + OC = 0.

772. В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его сторонами: АB = m, BC = n, CD = р, DE = q и EA = r. Построить векторы: 1) m — n + p — q + r; 2)m + 2р + 1/2r; 3) 2m + 1/2n — Зр — q + 2r.

1) m + n + р; 2) m + n + 1/2p;

3) 1/2m + 1/2n + р; 4) m + n — р;

774. Три силы М, N и Р, приложенные к одной точке, имеют взаимно перпендикулярные направления. Определить величину их равнодействующей R, если известно, что |М| = 2кГ, |N| = 10 кГ и |Р| = 11 кГ.

777. Определить, при каких значениях α, β векторы а = 2i + 3j + βk и b = ai — 6j + 2k коллинеарны.

783. Дано разложение вектора с по базису i, j, k: с = 16i — 15j + 12k. Определить разложение по этому же базису вектора d, параллельного вектору с и противоположного с ним направления, при условии, что |d| = 75.

784. Два вектора а = и b = приложены к одной точке. Определить координаты вектора с, направленного по биссектрисе угла между векторами а и b, при условии, что |с| = 3√42.

785. Векторы АB = и АC = совпадают со сторонами треугольника ABC. Определить координаты векторов, приложенных к вершинам треугольника и совпадающих с его медианами AM, BN, СР.

786*). Доказать, что если р и q — какие угодно не- коллинеарные векторы, то всякий вектор, лежащий в их плоскости, может быть представлен в виде: a = αp + αq.

Доказать, что числа α и β векторами а, р и q определяются однозначно. (Представление вектора а в виде a = αp + βq называется разложением его по базису р, q; числа α и β называются коэффициентами этого разложения.)

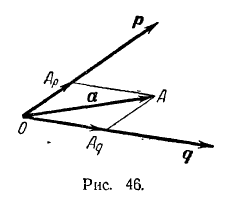
Доказательство. Приведем векторы а, р и q к общему началу, которое обозначим буквой О (рис. 46). Конец вектора а обозначим буквой А. Через точку А проведем прямую, параллельную вектору q. Точку пересечения этой прямой с линией действия вектора р обозначим через А_p. Аналогично, проводя через точку А прямую, параллельную вектору р, получим в пересечении с линией действия вектора q точку A_q.

По правилу параллелограмма получим:

Так как векторы OA _p и р лежат на одной прямой, то вектор OA _p может быть получен умножением вектора р на некоторое число α

Из равенств (1). (2) и (3) получаем: а = αр + βq. Тем самым возможность требуемого разложения доказана. Остается доказать, что коэффициенты α и β этого разложения определяются однозначно.

*) Задачи 786 и 792 существенны для правильного понимания остальных задач. Решение первой из них здесь приводится полностью.

Предположил, что вектор а имеет два разложения;

а = αр + βq, а = α’р + βq,

и, например, α’ ≠ α. Вычитая почленно одно из другого, получаем:

(α’ — α)р + (β’ — β)q = 0 или р = (β — β’)/(α’ — α)q.

Но это равенство означает коллинеарность векторов р и q, которые, однако, по условию являются неколлинеарными. Следовательно, неравенство α’ ≠ α невозможно. Аналогично доказывается, что невозможно неравенство β’ ≠ β. Таким образом,α’= α, β’ = β,т. е. двух различных разложений один и тот же вектор иметь не может.

790. Принимая в качестве базиса векторы AB = b и AC = с, совпадающие со сторонами треугольника ABC, определите разложение векторов, приложенных в вершинах треугольника и совпадающих с его медианами.

792. Доказать, что если р, q и r — какие угодно некомпланарные векторы ), то всякий вектор а пространства может быть представлен в виде: а = αр + βq + γr. Доказать, что числа α, β, γ векторами а, р, q и r определяются одйозначно. (Представление вектора а в виде a = αр + βq + γr называется разложением его по базису р, q, r. Числа α, β и γ называются коэффициентами этого разложения.)

*) Три вектора называются некомпланарными, если после приведения к общему началу они не лежат в одной плоскости.

Источник

Это не трапеция так как нет параллельных сторон.

Помогите пожалуйста?

Диагональ равнобокой трапеции равен 15см, а средняя линяя трапеции равна4см.

Найдите высоту трапеции.

Верхнее основание равнобедренной трапеции равно 28 см а высота 48 см?

Верхнее основание равнобедренной трапеции равно 28 см а высота 48 см.

Найти диагональ трапеции если она перпендикулярна боковой стороне.

Даны координаты вершины треугольника АВС?

Даны координаты вершины треугольника АВС.

В равнобедренной трапеции угол между боковой стороной и высотой равен проведенной из вершины тупого угла равен 23 градуса?

В равнобедренной трапеции угол между боковой стороной и высотой равен проведенной из вершины тупого угла равен 23 градуса.

Найдите углы трапеции.

Помогите пожалуйста(рисунок обязательно)?

Помогите пожалуйста(рисунок обязательно)!

Точка М равноудалена от всех вершин прямоугольного треугольника, катеты которого 6 см и 8 см.

Расстояние от точки М до плоскости треугольника = 12 см.

Найти расстояние от точки М до вершин треугольника.

Существует ли четырехугольник, у которого можно изменить положение любой вершины, оставив три другие на месте, так, что получившиеся четыре точки служат вершинами четыреугольника, равного исходному?

Существует ли четырехугольник, у которого можно изменить положение любой вершины, оставив три другие на месте, так, что получившиеся четыре точки служат вершинами четыреугольника, равного исходному.

Найти площадь трапеции с основаниями 4см и 6см, высотой 3см?

Найти площадь трапеции с основаниями 4см и 6см, высотой 3см.

Как найти высоту трапеции?

Как найти высоту трапеции.

Основы равнобедренной трапеции равны 4 см и 16 см?

Основы равнобедренной трапеции равны 4 см и 16 см.

Точка О равноудалена от всех сторон трапеции АВСD на 3 см.

Найти расстояние от данной точки до всех сторон трапеции.

Решение с подробными вычислениями на фото. Порядок действий для ясности вылелила желтым маркером.

А) 3 8 / 100 б) 4 75 / 100 в) 2 2 / 1000 г) 12 4 / 100 д) 5 / 100 е) 5 2 / 10.

2. д = 3см ш = 9 см ответ : 3см, 9см.

Источник

Это не трапеция так как нет параллельных сторон.

По какой формуле, зная высоту и среднюю линию треугольника или трапеции, можно найти их площадь?

По какой формуле, зная высоту и среднюю линию треугольника или трапеции, можно найти их площадь?

В равнобокой трапеции высота проведённая из вершины тупого угла делит большое основание на отрезки 8 и 32 см?

В равнобокой трапеции высота проведённая из вершины тупого угла делит большое основание на отрезки 8 и 32 см.

Найдите длины оснований трапеции.

Меньшее основание равнобедренной трапеции равно 6√2, точка пересечения диагоналий делит высоту трапеции в отношение 1 : 3, а центр описанной окружности лежит на большем основании?

Меньшее основание равнобедренной трапеции равно 6√2, точка пересечения диагоналий делит высоту трапеции в отношение 1 : 3, а центр описанной окружности лежит на большем основании.

Найдите высоту трапеции.

Даны координаты вершины треугольника АВС?

Даны координаты вершины треугольника АВС.

В равнобедренной трапеции угол между боковой стороной и высотой равен проведенной из вершины тупого угла равен 23 градуса?

В равнобедренной трапеции угол между боковой стороной и высотой равен проведенной из вершины тупого угла равен 23 градуса.

Найдите углы трапеции.

Дана трапеция ABCD?

Дана трапеция ABCD.

Существует ли четырехугольник, у которого можно изменить положение любой вершины, оставив три другие на месте, так, что получившиеся четыре точки служат вершинами четыреугольника, равного исходному?

Существует ли четырехугольник, у которого можно изменить положение любой вершины, оставив три другие на месте, так, что получившиеся четыре точки служат вершинами четыреугольника, равного исходному.

Найти площадь трапеции с основаниями 4см и 6см, высотой 3см?

Найти площадь трапеции с основаниями 4см и 6см, высотой 3см.

Как найти высоту трапеции?

Как найти высоту трапеции.

Решение с подробными вычислениями на фото. Порядок действий для ясности вылелила желтым маркером.

А) 3 8 / 100 б) 4 75 / 100 в) 2 2 / 1000 г) 12 4 / 100 д) 5 / 100 е) 5 2 / 10.

2. д = 3см ш = 9 см ответ : 3см, 9см.

Источник

Проверить что четыре точки А(3;-1;2) В(1;2;-1) С(-1;1;-3) D(3;-5;3) служат вершинами трапеции …

Проверить что точки A(-4 ;-3) B (-5 ;0) C (5; 6) D (1 ;0) служат вершинами трапеции и найти ее высоту.

Ваш комментарий к ответу:

Конфиденциальность: Ваш электронный адрес будет использоваться только для отправки уведомлений.

Чтобы избежать проверки в будущем, пожалуйста

Ответ или решение 1

Пусть дан четырёхугольник АВСD с вершинами в A(– 4; – 3) B (– 5; 0) C (5; 6) и D (1; 0). Чтобы проверить, является ли он трапецией, необходимо убедиться, что какая-то пара из противолежащих сторон образуют коллинеарные векторы. Найдём координаты векторов ВС и АD, для ВС: х = 5 + 5 = 10; у = 6 + 0 = 6; для АD: х = 1 + 4 = 5; у = 0 + 3 = 3. Поскольку координаты векторов пропорциональные, то векторы коллинеарные, а стороны параллельные: ВС | | АD, значит АВСD – трапеция.

Проведём из вершины D к основанию ВС высоту DК: ВС ⏊ DК. Запишем уравнение прямой ВС: (х – (– 5))/(5 – (– 5)) = (у – 0)/(6 – 0) или у = 0,6 ∙ х + 3. Найдём расстояние DК от точки D до этой прямой:

DК = |0,6 ∙ 1 + (– 1) ∙ 0 + 3| : √(0,6² + (– 1)²) = 9 ∙ √34/17 ≈ 3,09.

Вот собственно и ничего сложного.

Проверить параллельность двух прямых легко: должно соблюдаться равенство:
(Ya2 — Ya1) * (Xb2 — Xb1) = (Yb2 — Yb1) * (Xa2 — Xa1), где
Ya1 — координата игрек первой точки прямой а (с остальными думаю понятно)

Длинну отрезка находим так:
L = sqr((X2 — X1)^2 + (Y2-Y1)^2)

Проверить что четыре точки служат вершинами трапеции Ссылка на основную публикацию

Похожие вопросы

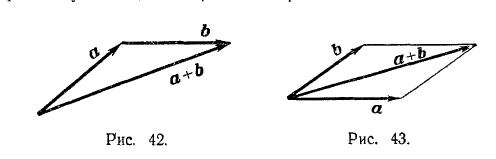
Математика

Источник

• таракан на теле примета →