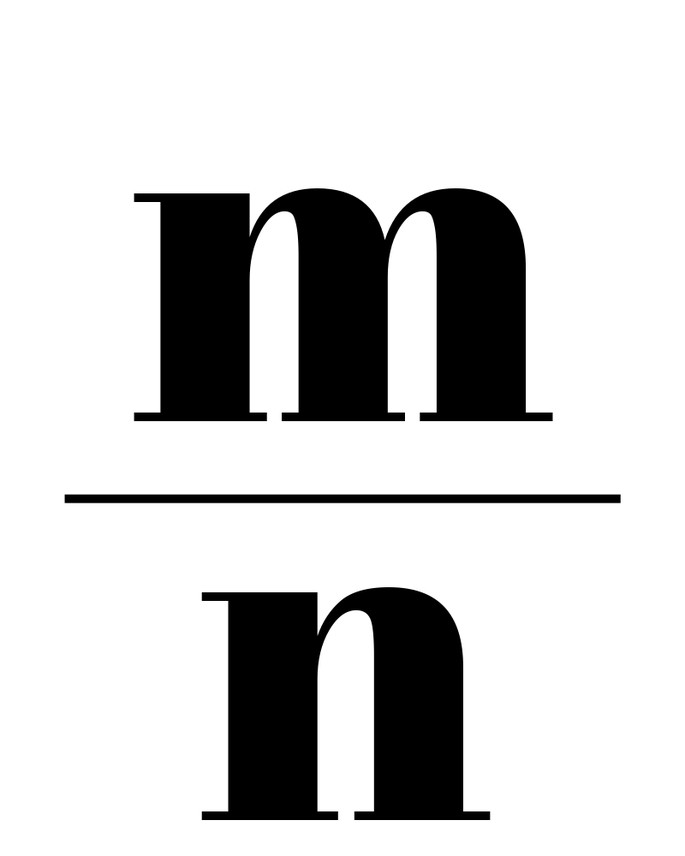Приведите пример двух различных иррациональных чисел таких что их сумма рациональное число
Иррациональные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами