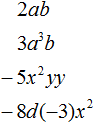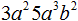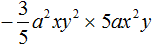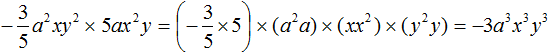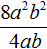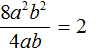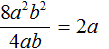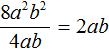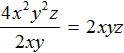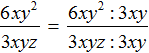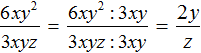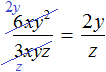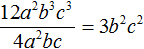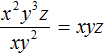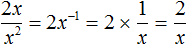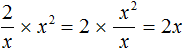Приведите одночлен к стандартному виду чему равна степень одночлена 25a4 3a3 2

Одночлены

Определения и примеры

Приведём ещё примеры одночленов:

Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 5 2 является одночленом.

Приведение одночлена к стандартному виду

Рассмотрим следующий одночлен:

Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.

Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.

Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Итак, приведём одночлен 3a 2 5a 3 b 2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:

Мы привели одночлен 3a 2 5a 3 b 2 к стандартному виду. В результате получили одночлен 15a 5 b 2

Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.

Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc

Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.

Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.

Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.

Пример 1. Привести одночлен 5xx3ya 2 к стандартному виду

Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:

Пример 2. Привести одночлен 2m 3 n × 0,4mn к стандартному виду

Перемножим числа, переменные и степени по отдельности.

Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m 3 × m и n × n

Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:

Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.

Сложение и вычитание одночленов

Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.

Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.

Пример 1. Сложить одночлены 6a 2 b и 2a 2 b

Сложим коэффициенты 6 и 2, а буквенную часть 6a 2 b оставим без изменений

Пример 2. Вычесть из одночлена 5a 2 b 3 одночлен 2a 2 b 3

Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:

Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:

Умножение одночленов

Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 1. Перемножить одночлены 5x и 8y

Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:

Пример 2. Перемножить одночлены 5x 2 y 3 и 7x 3 y 2 c

Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:

Пример 3. Перемножить одночлены −5a 2 bc и 2a 2 b 4

Пример 4. Перемножить одночлены x 2 y 5 и (−6xy 2 )

Пример 5. Найти значение выражения

Деление одночленов

Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.

Например, разделим одночлен 8a 2 b 2 на одночлен 4ab. Запишем это деление в виде дроби:

Первый одночлен 8a 2 b 2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.

Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.

Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.

В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:

Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:

Пример 2. Разделить одночлен 12a 2 b 3 c 3 на одночлен 4a 2 bc

Пример 3. Разделить одночлен x 2 y 3 z на одночлен xy 2

Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.

и такое частное при перемножении с делителем x 2 будет давать в результате делимое 2x

Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное 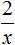целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.

Возведение одночлена в степень

Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.

Пример 1. Возвести одночлен xy во вторую степень.

Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена

Пример 2. Возвести одночлен −5a 3 b во вторую степень.

Пример 3. Возвести одночлен − a 2 bc 3 в пятую степень.

В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:

Пример 4. Представить одночлен 4x 2 в виде одночлена, возведённого в квадрат.

Пример 5. Представить одночлен 121a 6 в виде одночлена, возведённого в квадрат.

Таким образом, если произведение 11a 3 возвести во вторую степень, то получится 121a 6

(11a 3 ) 2 = 11 2 × (a 3 ) 2 = 121a 6

Разложение одночлена на множители

Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.

Пример 1. Разложить одночлен 3a 3 b 2 на множители

Данный одночлен можно разложить на множители 3, a, a, a, b, b

Либо степень b 2 можно не раскладывать на множители b и b

В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.

Пример 2. Разложить одночлен 10a 2 b 3 c 4 на множители.

Источник

Приведение одночлена к стандартному виду, примеры, решения

Начальные сведения об одночленах содержат уточнение, что любой одночлен возможно привести к стандартному виду. В материале ниже мы рассмотрим этот вопрос подробнее: обозначим смысл данного действия, определим шаги, позволяющие задать стандартный вид одночлена, а также закрепим теорию решением примеров.

Значение приведения одночлена к стандартному виду

Запись одночлена в стандартном виде позволяет более удобно работать с ним. Зачастую одночлены задаются в нестандартном виде, и тогда появляется необходимость осуществления тождественных преобразований для приведения заданного одночлена в стандартный вид.

Приведение одночлена к стандартному виду – это выполнение соответствующих действий (тождественных преобразований) с одночленом с целью записи его в стандартном виде.

Способ приведения одночлена к стандартному виду

Из определения следует, что одночлен нестандартного вида представляет собой произведение чисел, переменных и их степеней, при этом возможно их повторение. В свою очередь, одночлен стандартного вида содержит в своей записи только одно число и неповторяющиеся переменные или их степени.

Чтобы привести нестандартный одночлен в стандартный вид, необходимо использовать следующее правило приведения одночлена к стандартному виду:

Примеры и их решение

Задан одночлен 3 · x · 2 · x 2 . Необходимо привести его к стандартному виду.

Решение

Осуществим группировку числовых множителей и множителей с переменной х, в результате заданный одночлен примет вид: ( 3 · 2 ) · ( x · x 2 ) .

Решение

Краткая запись всех действий выглядит так:

Ответ:

Источник

Стандартный вид многочлена

Калькулятор отображает многочлен нескольких переменных в стандартном виде. Есть возможность выбрать порядок одночленов.

Калькулятор далее представляет входной многочлен нескольких переменных в стандартном виде (раскрывает скобки, возводит в степень и приводит подобные члены). Переменные многочлена можно задать строчными английскими буквами или в виде мультииндекса (массива степеней переменных). Например, записи 3a^2bd +c и 3[2 1 0 1] + [0 0 1] эквивалентны. Вывод результата возможен в виде буквенной и индексной записях, либо в также в виде мультииндекса. Также выводится степень многочлена и вектор степеней одночленов. Коэффициенты результирующего многочлена рассчитываются в поле рациональных или вещественных чисел.

Стандартный вид многочлена

Одночлен

Пример: мультииндекс одночлена x 2 y 3 z = (2,3,1)
Степенью одночлена называется сумма всех показателей степеней переменных этого одночлена:

Например, степень одночлена: x 2 y 3 z равна 2+3+1 = 6

Многочлен

Многочлен в стандартном виде это конечная сумма одночленов помноженных на коэффициенты:

Степенью многочлена deg(f) называется максимальная степень |a| всех одночленов многочлена, с ненулевыми коэффициентами.
В отличие от многочленов одной переменной, многочлены многих переменных могут иметь несколько одночленов с одинаковой степенью.
В связи с этим возникает вопрос определения порядка на множестве членов многочлена.

Порядок членов многочлена 1

Известно несколько способов задания порядка членов многочлена.

Лексикографический порядок

Градуированный лексикографический порядок

Градуированный обратный лексикографический порядок

Д. Кокс, О. Литл, Д. О’Ши Идеалы, многообразия и алгоритмы. Введение в вычислительные аспекты алгебраической геометрии и коммутативной алгебры. Пер. с английского. М.: Мир 2000 ↩

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Упрощение многочлена.
Умножение многочленов.

С помощью данной математической программы вы можете упростить многочлен.
В процессе работы программа:
— умножает многочлены
— суммирует одночлены (приводит подобные)
— раскрывает скобки
— возводит многочлен в степень

Программа упрощения многочленов не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы вы могли проконтролировать свои знания по математике и/или алгебре.

Данная программа может быть полезна учащимся общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Немного теории.

Произведение одночлена и многочлена. Понятие многочлена

Сумму одночленов называют многочленом. Слагаемые в многочлене называют членами многочлена. Одночлены также относят к многочленам, считая одночлен многочленом, состоящим из одного члена.

Сумму нескольких многочленов можно преобразовать (упростить) в многочлен стандартного вида.

Иногда члены многочлена нужно разбить на группы, заключая каждую группу в скобки. Поскольку заключение в скобки — это преобразование, обратное раскрытию скобок, то легко сформулировать правила раскрытия скобок:

Если перед скобками ставится знак «+», то члены, заключаемые в скобки, записываются с теми же знаками.

Если перед скобками ставится знак «-», то члены, заключаемые в скобки, записываются с противоположными знаками.

Преобразование (упрощение) произведения одночлена и многочлена

Произведение одночлена и многочлена тождественно равно сумме произведений этого одночлена и каждого из членов многочлена.

Этот результат обычно формулируют в виде правила.

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый из членов многочлена.

Мы уже неоднократно использовали это правило для умножения на сумму.

Произведение многочленов. Преобразование (упрощение) произведения двух многочленов

Вообще, произведение двух многочленов тождественно равно сумме произведении каждого члена одного многочлена и каждого члена другого.

Обычно пользуются следующим правилом.

Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и сложить полученные произведения.

Формулы сокращенного умножения. Квадраты суммы, разности и разность квадратов

Полученные тождества полезно запомнить и применять без промежуточных выкладок. Помогают этому краткие словесные формулировки.

Эти три тождества позволяют в преобразованиях заменять свои левые части правыми и обратно — правые части левыми. Самое трудное при этом — увидеть соответствующие выражения и понять, чем в них заменены переменные а и b. Рассмотрим несколько примеров использования формул сокращенного умножения.

Источник

Многочлен стандартного вида

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение многочлена

Многочлен — это сумма одночленов. Получается, что многочлен — не что иное, как несколько одночленов, собранных «под одной крышей».

Одночлен — это частный случай многочлена.

Рассмотрим примеры многочленов:

Если многочлен состоит из двух одночленов, его называют двучленом:

Многочлен — это сумма одночленов, поэтому знак «минус» относится к числовому коэффициенту одночлена. Именно поэтому мы записываем – 3×2, а не просто 3×2.

Этот же многочлен можно записать вот так:

Это значит, что каждый одночлен важно рассматривать вместе со знаком, который перед ним стоит.

Многочлен вида 10x – 3×2 + 7 называется трехчленом.

Линейный двучлен — это многочлен первой степени: ax + b. a и b здесь — некоторые числа, x — переменная.

Если разделить многочлен с переменной x на линейный двучлен x – b (где b — некоторое положительное или отрицательное число) — остаток будет только многочленом нулевой степени. То есть некоторым числом N, которое можно определить без поиска частного.

Если многочлен содержит обычное число — это число является свободным членом многочлена.

Свободный член многочлена не имеет буквенной части. Кроме того, любое числовое выражение — это многочлен. Например, вот такие числовые выражения — тоже многочлены:

Такие выражения состоят из свободных членов.

Многочлен стандартного вида

Недостаточно просто знать, что такое многочлен и что такое одночлен. Это целая алгебраическая экосистема, где у всего есть названия, определения и особенности.

Давайте разберемся, что такое многочлен стандартного вида. Многочленом стандартного вида называют многочлен, каждый член которого имеет одночлен стандартного вида и не содержит подобных членов.

Получается, что всякий многочлен можно привести к стандартному виду. Таким образом можно получить многочлен, работать с которым гораздо проще и приятнее.

К стандартному виду многочлен приводится очень просто. Нужно лишь привести в нем подобные слагаемые.

Подобные слагаемые — это подобные члены многочлена. Приведение подобных слагаемых в многочлене — приведение его подобных членов. Тут же возникает резонный вопрос: Что такое подобные члены многочлена? Это члены с одинаковой буквенной частью.

Давайте разберем на примере, как «нестандартный» многочлен приводится к стандартному виду.

Дан красавец многочлен: 3x + 5xy2 + x – xy2

Приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Как видите, в получившемся многочлене нет подобных членов. Такой многочлен — это многочлен стандартного вида.

Степень многочлена

Многочлен может иметь степень — имеет на это полное право.

Степень многочлена стандартного вида — это наибольшая из степеней, входящих в него одночленов.

Из определения можно сделать вывод, что степень многочлена возможно определить только после приведения его к стандартному виду.

Рассмотрим на примере:

Дан многочлен 6x + 4xy2 + x + xy2

Сначала приводим многочлен к стандартному виду — для этого приводим подобные слагаемые:

Получаем многочлен стандартного вида 6x + 4xy2 + x + xy2 = 7x + 5xy2.

Отсюда делаем вывод, что многочлен 7x + 5xy2 — многочлен второй степени.

Кроме того, можно сделать вывод, что и исходный многочлен 6x + 4xy2 + x + xy2 — многочлен второй степени, поскольку оба многочлена равны друг другу.

В некоторых случаях необходимо сначала привести к стандартному виду одночлены многочлена, а затем уже и сам многочлен.

Пример:

Получившийся многочлен без труда приводим к стандартному виду. Приводим подобные слагаемые:

Коэффициенты многочлена

Коэффициенты членов многочлена — это числа, которые указаны перед переменными множителями. Если перед переменной нет числа, то коэффициент этого члена = 1.

Иными словами — коэффициенты членов многочлена — это члены многочлена, представленные в виде стандартных одночленов.

Например:

Все одночлены имеют стандартный вид. 2, 5 и 18 — коэффициенты членов данного многочлена.

Кажется, со стандартным видом многочлена все понятно. Чтобы без труда приводить любой многочлен к стандартному виду, нужно потренироваться, ведь в 7 классе только и разговоров, что о многочленах. Давайте разберем несколько примеров. Попробуйте решить их самостоятельно, сверяясь с ответами.

Задание раз. Приведите многочлен к стандартному виду и определите его степень: 4x + 6xy2 + x – xy2.

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Получаем многочлен стандартного вида: 4x + 6xy2 + x – xy2 = 5x + 5xy2.

Ответ: стандартный вид многочлена 5x + 5xy2. Данный многочлен — многочлен второй степени.

Многочлен приведен к стандартному виду.

Как решаем: приведем подобные слагаемые. Для этого найдем все члены с одинаковыми буквенными составляющими:

Разобраться в многочленах не так-то просто. В этой теме немало нюансов и подводных камней. Чтобы не запутаться в множестве похожих одно на другое определений, побольше практикуйтесь. Чтобы перейти на следующую ступень и начать выполнение арифметических действий с многочленами, важно научиться приводить многочлен к стандартному виду.

Источник