Принцип суперпозиции означает что

Принцип суперпозиции

При́нцип суперпози́ции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:

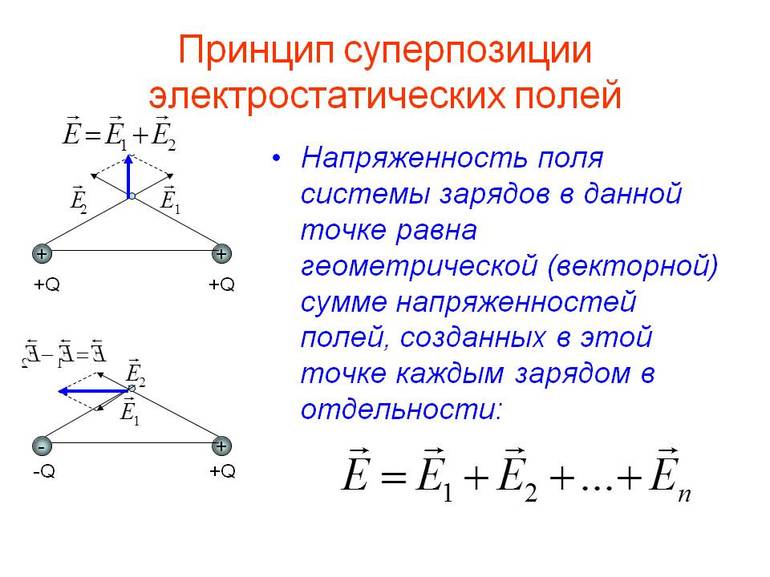
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

Принцип суперпозиции в электродинамике

Принцип суперпозиции является следствием, прямо вытекающем из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию a priori. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.

Другим следствием линейности уравнений Максвелла является тот факт, что лучи света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назвать принципом суперпозиции в оптике.

Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, то есть уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушение принципа суперпозиции.

Примеры нарушения электродинамического принципа суперпозиции

Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если поляризуемость или намагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой нелинейной среде.

В некоторых случаях эти нелинейности невелики, и принцип суперпозиции с некоторой степенью приближения может выполняться. В других случаях нарушение принципа суперпозиции велико и может приводить к принципиально новым явлениям. Так, например, два луча света, распространяющиеся в нелинейной среде, могут изменять траекторию друг друга. Более того, даже один луч света в нелинейной среде может воздействовать сам на себя и изменять свои характеристики. Многочисленные эффекты такого типа изучает нелинейная оптика.

Принцип суперпозиции нарушается также в вакууме при учёте квантовых явлений. В квантовой электродинамике фотон может на некоторое время превратиться в электрон-позитронную пару, которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы (рассеяние света на свете и другие процессы нелинейной электродинамики) наблюдались экспериментально. [источник не указан 460 дней]

Отсутствие принципа суперпозиции в нелинейных теориях

Тот факт, что уравнения классической электродинамики линейны, является скорее исключением, чем правилом. Многие фундаментальные теории современной физики являются нелинейными. Например, квантовая хромодинамика — фундаментальная теория сильных взаимодействий — является разновидностью теории Янга — Миллса, которая нелинейна по построению. Это приводит к сильнейшему нарушению принципа суперпозиции даже в классических (неквантованных) решениях уравнений Янга — Миллса.

Другим известным примером нелинейной теории является общая теория относительности. В ней также не выполняется принцип суперпозиции. Например, Солнце притягивает не только Землю и Луну, но также и само взаимодействие между Землёй и Луной. Впрочем, в слабых гравитационных полях эффекты нелинейности слабы, и для повседневных задач приближённый принцип суперпозиции выполняется с высокой точностью.

Наконец, принцип суперпозиции не выполняется, когда речь идёт о взаимодействии атомов и молекул. Это можно пояснить следующим образом. Рассмотрим два атома, связанных общим электронным облаком. Поднесем теперь точно такой же третий атом. Он как бы оттянет на себя часть связывающего атомы электронного облака, и в результате связь между первоначальными атомами ослабнет. То есть, присутствие третьего атома изменяет энергию взаимодействия пары атомов. Причина этого проста: третий атом взаимодействует не только с первыми двумя, но и с той «субстанцией», которая обеспечивает связь первых двух атомов.

Нарушение принципа суперпозиции во взаимодействиях атомов в немалой степени приводит к тому удивительному разнообразию физических и химических свойств веществ и материалов, которое так трудно предсказать из общих принципов молекулярной динамики.

Источник

Принцип суперпозиции

* Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.

Любое сложное движение можно разделить на два и более простых.Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть векторная сумма напряженности полей отдельных зарядов.

Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:

* Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.

Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.

Связанные понятия

В квантовой механике импульс, как и все другие наблюдаемые физические величины, определяется как оператор, который действует на волновую функцию.

Ниже приведены примеры уравнений непрерывности, которые выражают одинаковую идею непрерывного изменения некоторой величины. Уравнения непрерывности — (сильная) локальная форма законов сохранения.

Эта статья о физическом понятии. О более общем значении термина, см. статью СкалярСкалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д.Скалярная величина, или скаляр согласно математическому энциклопедическому словарю.

При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.

Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость.

Источник

Принцип суперпозиции — определение, формула и значение

Большая часть популярных доктрин, открытых на сегодня, описывает довольно своеобразные явления — механические движения, тепловые процессы, электрические явления и так далее. Однако существуют мнения, которые относятся ко всем областям физических явлений. Одним из таких теоретических понятий считается принцип суперпозиции (ПС).

Общая концепция

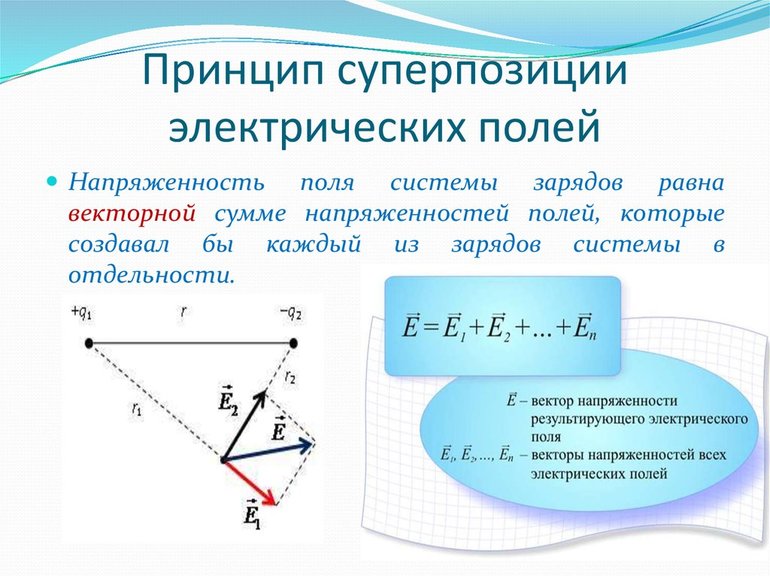
Можно столкнуться с принципом суперпозиции всякий раз, когда есть больше одного источника электростатического поля. Затем в каждой точке пространства происходит сборка линий, поступающих из каждого источника. Поскольку интенсивность является вектором, в каждой точке добавляют друг к другу векторы любого из источников, то есть учитывают их значения направления и отдачи.

Самый простой способ — добавить параллельные векторы, затем просто вычесть значения, и уравнение становится скалярным. В любом ином случае угол между векторами должен быть принят во внимание. В общем, векторное уравнение суперпозиции полей может быть сохранено через знак суммы. Определяется принцип суперпозиции формулой:

E = ∑ − → E i E → = ∑ E i →

Напряжение электростатического поля

Стоит рассмотреть напряжённость электрического поля, принцип суперпозиции, создаваемый двумя начальными зарядами одновременно в любой точке пространства. Например, есть 2 источника, положительный заряд и отрицательный, примерно одинаковых значений, то есть диполь. Нужно выяснить результирующую напряжённость электростатического поля в 3 точках.

Сначала отмечают вспомогательные линии, которые проходят через каждую из трёх точек и оба источника. Затем по очереди рисуют интенсивность в каждой из точек, основываясь на обеих линиях. Стоит отметить важную информацию о принципе суперпозиции электрических полей: направление и возврат вектора интенсивности будут такими же, как и у линии, действующей на положительный заряд, размещённый в этой точке.

Нужно рассмотреть первый пункт, поскольку пробный заряд всегда +. Интенсивность от источника плюсового будет влево. Он представлен в виде вектора E1 +. Ток от источника отрицания будет отправлен в то же место, поскольку противоположные заряды притягивают друг друга. Он как вектор E1-. Поскольку сила электростатического поля будет вектором, результирующий ток — сумма двухкомпонентных линий. Он в виде E1. Первая точка близка к положительному источнику, потому вектор интенсивности от него больше, чем отрицательный заряд.

Разделяя их, однажды в точке 2 сила, исходящая от нагрузки отрицательного Е2, направляется на источник, а исходящая от нагрузки положительного Е2 + направляется от него. Точка 2 находится на одинаковом расстоянии от обоих полей, поэтому значения линий напряжения E2 + E2 равны. Так как векторы не параллельны, применяют метод параллелограмма для их добавления — рисуют его стороны, что являются векторами интенсивности (ВИ). Сумма — диагональ, исходящая из начала. В результате получают E2.

Точно так же это будет для пункта 3. E3 + от источника, E3 направлена наоборот. Длинная диагональ представляет собой сумму векторов компонентов, то есть результирующей интенсивности в точке E3.

Полученные уравнения являются векторными, поэтому в расчётах следует учитывать не только значение, но также их направление и возврат. Это означает, что для трёх точек только одна с номером 1 может быть легко представлена в скалярной форме. Поскольку векторы E1 + E1 находятся на одной прямой, они параллельны. Их значения должны быть добавлены, потому что их возвраты, то есть стрелки, будут в одном направлении. Следовательно, в этом случае скалярное уравнение выглядит так же, как вектор.

Введение в волновую суперпозицию

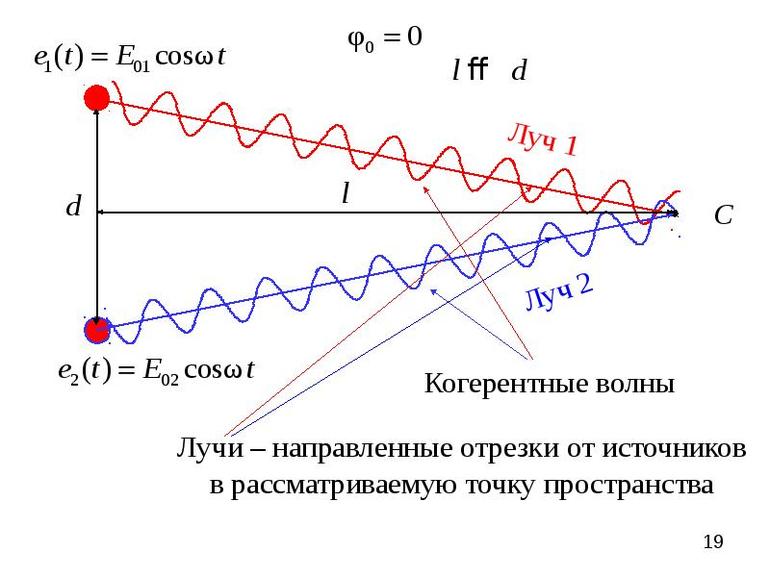
Волны окружают нас, и их присутствие влияет на ряд явлений. Можно представить себе нахождение в лодке и слышимую сирену корабля. В этом случае можно получить звуковую волну непосредственно, а также ту, которая отражается от морской воды. Чтобы понять это, нужно сосредоточиться на базовой концепции суперпозиции, а также на знаниях, связанных с теоремой.

Пример струнной волны для определения суперпозиции на основе теоремы поможет лучше всё понять. В соответствии с этим чистое перемещение любого компонента строки в течение заданного времени равно алгебраическому набору смещений, вызванных каждой волной. Потому такой метод добавления отдельных сигналов для оценки частоты называется принципом суперпозиции.

ПС выражается утверждением, что перекрывающиеся волны алгебраически добавляются для создания результирующей линии. Исходя из этого (f1, f2 …., fn), они не мешают движению друг друга. Следовательно, суперпозиция волн может привести к следующим трем последствиям:

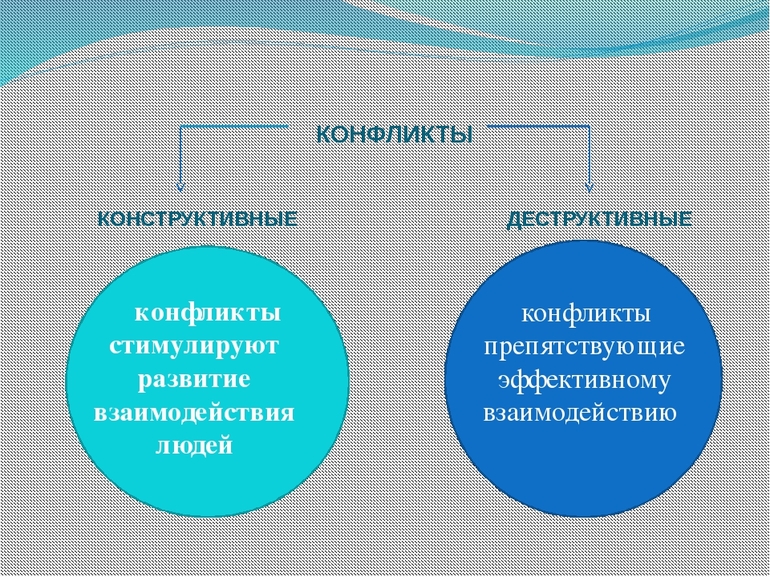
Конструктивное и деструктивное вмешательство

Это когда две волны движутся в определённом или одном и том же направлении. Согласно ПС, последующее смещение можно записать в виде решения:

y (x, t) = y m sin (kx-ωt) + y m sin (kx-ωt+ϕ) = 2 y m cos (ϕ/2) sin (kx-ωt+ϕ/2)

Эта волна имеет развитие амплитуды, которая зависит от фазы (ϕ). Считается, что две линии находятся в фазе (ϕ = 0). Они мешают конструктивно. Кроме того, результирующая часть имеет двойную амплитуду по сравнению с отдельными волнами. С другой стороны, задача, когда две линии имеют противоположную фазу (ϕ = 180). Они оказывают разрушающее воздействие на друг друга.

Две синусоиды в противоположных направлениях

Бегущая волна распространяется из одного места в другое, но стоячая выглядит как неподвижная. Предположим, что две линии (имеющие одинаковые свойства — амплитуду, длину и частоту) передвигаются в противоположных направлениях.

Основываясь на системе суперпозиции, конечная амплитуда может быть записана как формулировка:

y (x, t) = y m sin (kx-ωt) + y m sin (kx+ωt) = 2 y m sin (kx) cos (ωt)

Согласно теореме о суперпозиции, несколько волн не называют бегущими, поскольку зависимость положения и времени делится. В этом случае амплитуда, в зависимости от точки или местоположения, составляет 2ymsin (kx). Она не будет смещаться, но сможет стоять с колебанием вверх и вниз на основе независимого cos (wt).

Линии электропередач

Электрическое поле в пространстве обычно можно создать силовыми линиями. Понятие было введено М. Фарадеем при изучении закона взаимодействия магнетизма. Затем концепцию индукции разработал Джон Максвелл.

Важные особенности магнитной теории заключаются в следующем:

Принцип супербора

С точки зрения квантовой механики, этот принцип содержит большое количество особенностей, которые нельзя просто принять. Это связано с тем, что фактически эта отрасль физики имеет дело, прежде всего, с другими состояниями объекта. С точки зрения традиционной механики, они должны быть элементарно взаимоисключающими. Принцип суперпозиции, который на квантовом уровне еще не полностью понят ученым, подразумевает, среди прочего, необходимость суперотбора, то есть главного класса фактора, который оказывает наибольшее влияние на пучок сил в определенный момент.

Подводя итоги, можно сказать следующее: в тот момент, когда поток электростатического поля больше, чем 1 заряд, то в каждой точке пространства поля всех линий собираются, и результирующий ВИ является суммой всех компонентов.

Источник

Суперпозиции принцип

С. п. играет исключительную роль в механике (например, векторное сложение по правилу параллелограмма), в теории колебаний, теории цепей, квантовой механике и других разделах физики и техники. 2) В теории классических полей и квантовой теории — положение, согласно которому суперпозиция (то есть результат суммирования, наложения друг на друга) любых допустимых в данных условиях состояний физической системы (или возможных процессов в ней) является также допустимым состоянием (или соответственно возможным процессом). Так, классическое электромагнитное поле в вакууме удовлетворяет С.п.: сумма любого числа физически реализуемых полей есть тоже физически реализуемое электромагнитное поле. В силу С.п. электромагнитное поле, созданное совокупностью электрических зарядов и токов, равно сумме полей, создаваемых этими зарядами и токами по отдельности. Слабое гравитационное поле также с хорошей точностью подчиняется С. п.

В классической физике С. п. — приближённый принцип, вытекающий из линейности уравнений движения соответствующих систем (что обычно является хорошим приближением для описания реальных систем), например Максвелла уравнений (См. Максвелла уравнения) для электромагнитного поля. Таким образом, он вытекает из более глубоких динамических принципов и поэтому не является фундаментальным. Он и не универсален. Так, достаточно сильное гравитационное поле не удовлетворяет С. п., поскольку оно описывается нелинейными уравнениями Эйнштейна (см. Тяготение); макроскопическое электромагнитное поле в веществе, строго говоря, также не подчиняется С. п. в силу зависимости (иногда существенной) диэлектрической и магнитной проницаемостей от внешнего поля (например, в ферромагнетике (См. Ферромагнетики)) и т. д.

В квантовой механике С. п. — фундаментальный принцип, один из основных её постулатов, определяющий вместе с Неопределённостей соотношением структуру математического аппарата теории. Из С. п. следует, например, что состояния квантовомеханической системы должны изображаться векторами линейного пространства (см. Квантовая механика), в частности волновыми функциями (См. Волновая функция); что Операторы физических величин должны быть линейными и т. д. С. п. утверждает, что если квантовомеханическая система может находиться в состояниях, описываемых волновыми функциями ψ₁,ψ₂. ψ_n, то физически допустимой будет и суперпозиция этих состояний, то есть состояние, изображаемое волновой функцией

Из С. п. следует, что любая волновая функция может быть разложена в сумму (вообще говоря, бесконечную) собственных функций оператора любой физической величины; при этом квадраты модулей коэффициентов в разложении имеют смысл вероятностей обнаружить на опыте соответствующие значения этой величины. Суперпозиция состояний ψ_i определяется, однако, не только модулями коэффициентов c_i, но и их относительными фазами (при различных относительных фазах чисел с_i, результирующие состояния оказываются различными). Поэтому суперпозиция ψ = ∑_i c_i ψ_i является результатом интерференции состояний ψ_i (см., например, Дифракция частиц). Квантовый С. п. лишён наглядности, характерной для С. п. в классической физике, так как в квантовой теории в суперпозиции участвуют (складываются) альтернативные, с классической точки зрения взаимоисключающие друг друга состояния. С. п. отражает волновую природу микрочастиц и выполняется в нерелятивистской квантовой механике без исключений.

В релятивистской квантовой теории, рассматривающей процессы, в которых могут происходить взаимопревращения частиц, С. п. должен быть дополнен так называемыми правилами суперотбора. Так, суперпозиции состояний с разными значениями электрического, барионного, лептонного зарядов не предполагаются физически реализуемыми. Реализуемость таких суперпозиций означала бы, например, что физические свойства пучка частиц, в котором в некоторой пропорции присутствуют электроны и позитроны, не определяются однозначно динамическими характеристиками этих частиц, то есть что возможна интерференция состояний с разными значениями зарядов. Однако такая интерференция никогда не наблюдалась на опыте. Поэтому операторы физических величин не должны менять заряды. Это уточнение С. п. в релятивистской квантовой теории накладывает на матричные элементы операторов определённые ограничения, которые и называют правилами суперотбора.

Лит.: Дирак П. А. М., Принципы квантовой механики, пер. с англ., М., 1960; Л андау Л. Д., Лифшиц Е. М., Квантовая механика, 3 изд., М., 1974; Швебер С., Введение в релятивистскую квантовую теорию поля, [пер. с англ.], М., 1963.

Источник

Общая концепция

Можно столкнуться с принципом суперпозиции всякий раз, когда есть больше одного источника электростатического поля. Затем в каждой точке пространства происходит сборка линий, поступающих из каждого источника. Поскольку интенсивность является вектором, в каждой точке добавляют друг к другу векторы любого из источников, то есть учитывают их значения направления и отдачи.

Самый простой способ — добавить параллельные векторы, затем просто вычесть значения, и уравнение становится скалярным. В любом ином случае угол между векторами должен быть принят во внимание. В общем, векторное уравнение суперпозиции полей может быть сохранено через знак суммы. Определяется принцип суперпозиции формулой:

E = ∑ − → E i E → = ∑ E i →

Напряжение электростатического поля

Стоит рассмотреть напряжённость электрического поля, принцип суперпозиции, создаваемый двумя начальными зарядами одновременно в любой точке пространства. Например, есть 2 источника, положительный заряд и отрицательный, примерно одинаковых значений, то есть диполь. Нужно выяснить результирующую напряжённость электростатического поля в 3 точках.

Сначала отмечают вспомогательные линии, которые проходят через каждую из трёх точек и оба источника. Затем по очереди рисуют интенсивность в каждой из точек, основываясь на обеих линиях. Стоит отметить важную информацию о принципе суперпозиции электрических полей: направление и возврат вектора интенсивности будут такими же, как и у линии, действующей на положительный заряд, размещённый в этой точке.

Нужно рассмотреть первый пункт, поскольку пробный заряд всегда +. Интенсивность от источника плюсового будет влево. Он представлен в виде вектора E1 +. Ток от источника отрицания будет отправлен в то же место, поскольку противоположные заряды притягивают друг друга. Он как вектор E1-. Поскольку сила электростатического поля будет вектором, результирующий ток — сумма двухкомпонентных линий. Он в виде E1. Первая точка близка к положительному источнику, потому вектор интенсивности от него больше, чем отрицательный заряд.

Разделяя их, однажды в точке 2 сила, исходящая от нагрузки отрицательного Е2, направляется на источник, а исходящая от нагрузки положительного Е2 + направляется от него. Точка 2 находится на одинаковом расстоянии от обоих полей, поэтому значения линий напряжения E2 + E2 равны. Так как векторы не параллельны, применяют метод параллелограмма для их добавления — рисуют его стороны, что являются векторами интенсивности (ВИ). Сумма — диагональ, исходящая из начала. В результате получают E2.

Точно так же это будет для пункта 3. E3 + от источника, E3 направлена наоборот. Длинная диагональ представляет собой сумму векторов компонентов, то есть результирующей интенсивности в точке E3.

Полученные уравнения являются векторными, поэтому в расчётах следует учитывать не только значение, но также их направление и возврат. Это означает, что для трёх точек только одна с номером 1 может быть легко представлена в скалярной форме. Поскольку векторы E1 + E1 находятся на одной прямой, они параллельны. Их значения должны быть добавлены, потому что их возвраты, то есть стрелки, будут в одном направлении. Следовательно, в этом случае скалярное уравнение выглядит так же, как вектор.

Введение в волновую суперпозицию

Волны окружают нас, и их присутствие влияет на ряд явлений. Можно представить себе нахождение в лодке и слышимую сирену корабля. В этом случае можно получить звуковую волну непосредственно, а также ту, которая отражается от морской воды. Чтобы понять это, нужно сосредоточиться на базовой концепции суперпозиции, а также на знаниях, связанных с теоремой.

Пример струнной волны для определения суперпозиции на основе теоремы поможет лучше всё понять. В соответствии с этим чистое перемещение любого компонента строки в течение заданного времени равно алгебраическому набору смещений, вызванных каждой волной. Потому такой метод добавления отдельных сигналов для оценки частоты называется принципом суперпозиции.

ПС выражается утверждением, что перекрывающиеся волны алгебраически добавляются для создания результирующей линии. Исходя из этого (f1, f2 …., fn), они не мешают движению друг друга. Следовательно, суперпозиция волн может привести к следующим трем последствиям:

Конструктивное и деструктивное вмешательство

Это когда две волны движутся в определённом или одном и том же направлении. Согласно ПС, последующее смещение можно записать в виде решения:

y (x, t) = y m sin (kx-ωt) + y m sin (kx-ωt+ϕ) = 2 y m cos (ϕ/2) sin (kx-ωt+ϕ/2)

Эта волна имеет развитие амплитуды, которая зависит от фазы (ϕ). Считается, что две линии находятся в фазе (ϕ = 0). Они мешают конструктивно. Кроме того, результирующая часть имеет двойную амплитуду по сравнению с отдельными волнами. С другой стороны, задача, когда две линии имеют противоположную фазу (ϕ = 180). Они оказывают разрушающее воздействие на друг друга.

Две синусоиды в противоположных направлениях

Бегущая волна распространяется из одного места в другое, но стоячая выглядит как неподвижная. Предположим, что две линии (имеющие одинаковые свойства — амплитуду, длину и частоту) передвигаются в противоположных направлениях.

Основываясь на системе суперпозиции, конечная амплитуда может быть записана как формулировка:

y (x, t) = y m sin (kx-ωt) + y m sin (kx+ωt) = 2 y m sin (kx) cos (ωt)

Согласно теореме о суперпозиции, несколько волн не называют бегущими, поскольку зависимость положения и времени делится. В этом случае амплитуда, в зависимости от точки или местоположения, составляет 2ymsin (kx). Она не будет смещаться, но сможет стоять с колебанием вверх и вниз на основе независимого cos (wt).

Линии электропередач

Электрическое поле в пространстве обычно можно создать силовыми линиями. Понятие было введено М. Фарадеем при изучении закона взаимодействия магнетизма. Затем концепцию индукции разработал Джон Максвелл.

Важные особенности магнитной теории заключаются в следующем:

Принцип супербора

С точки зрения квантовой механики, этот принцип содержит большое количество особенностей, которые нельзя просто принять. Это связано с тем, что фактически эта отрасль физики имеет дело, прежде всего, с другими состояниями объекта. С точки зрения традиционной механики, они должны быть элементарно взаимоисключающими. Принцип суперпозиции, который на квантовом уровне еще не полностью понят ученым, подразумевает, среди прочего, необходимость суперотбора, то есть главного класса фактора, который оказывает наибольшее влияние на пучок сил в определенный момент.

Подводя итоги, можно сказать следующее: в тот момент, когда поток электростатического поля больше, чем 1 заряд, то в каждой точке пространства поля всех линий собираются, и результирующий ВИ является суммой всех компонентов.

Источник