Пример со сложением и вычитанием что делать первым
Порядок выполнения действий в выражениях без скобок
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно 7. Посчитать можно на счетных палочках, камнях, яблоках– результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Почему умножение первое?
Разберем математические действия на примере. Давайте собирать яблоки у бабушки на даче:
Все яблоки приностили бабушке, она укладывала их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
Получаем пример для школы, запись учетчика результатов работы:
50 + 50 + 50 + 5 + 5 + 7 =?;
Здесь можно применить группировку: 3 кучки по 50 яблок − это можно записать через операцию умножения: 3 ∙ 50.
Две кучки по 5 – это тоже можно записать через умножение.
И одна кучка 7 яблок.
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только яблоки. Нельзя сложить 50 яблок и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки – умножения. Совсем простыми словами – сначала выполняется умножение, а сложение уже потом. Если умножить 3кучки по 50 яблок каждая, то получится 150 яблок. А дальше их уже можно складывать с яблоками из других кучек.
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Порядок действий в выражениях без скобок
Для правильного вычисления выражений, в которых нужно произвести более одного действия, нужно знать порядок выполнения арифметических действий. Арифметические действия в выражении без скобок условились выполнять в следующем порядке:
В качестве примера рассмотрим следующее выражение:
Сначала необходимо выполнить возведение в степень (число 4 возвести в квадрат и число 2 в куб):
Затем выполняются умножение и деление (3 умножить на 16 и 8 разделить на 2):
И в самом конце, выполняются вычитание и сложение (из 48 вычесть 4 и к результату прибавить 20):
48 – 4 + 20 = 44 + 20 = 64
Первый способ

Запомните!
При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.
Второй способ

Запомните!
Если выражение содержит скобки, то сначала выполняют действия в скобках.
Внутри самих скобок действует правило порядка действий как в выражениях без скобок.
Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.
Задания для самостоятельного решения
Задание 1. Найдите значение выражения: 5 + 2 − 2 − 1 Решение

Показать решение Задание 2. Найдите значение выражения: 14 + (6 + 2 × 3) − 6 Решение

Показать решение Задание 3. Найдите значение выражения: 486 : 9 − 288 : 9 Решение

Показать решение Задание 4. Найдите значение выражения: 756 : 3 : 4 × 28 Решение

Показать решение Задание 5. Найдите значение выражения: 807 : 3 − (500 − 58 × 4) Решение
Дополнительные примеры
В данном разделе мы познакомимся с порядком действий, с выражениями со скобками и без них.
1) Если тебе нужно выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
Например,
В числовом выражении 3 арифметических действия: сложение, вычитание и вычитание.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни умножения ни деления, действия выполняют по порядку слева направо:
Полностью пример записываем так:
10 + 15 – 6 – 8 = 25 – 6 – 8 = 19 – 8 = 11
Например,
В числовом выражении 3 арифметических действия: деление, умножение и деление.
Определим порядок действий и запишем их над арифметическими знаками: так как нет ни сложения ни вычитания, действия выполняют по порядку слева направо:
Полностью пример записываем так:
15 : 5 • 4 : 6 = 3 • 4 : 6 = 12 : 6 = 2
2) Если тебе нужно выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим деление, потом умножение, затем вычитание и сложение.
Полностью пример записываем так:
10 – 15 : 3 + 6 • 8 = 10 – 5 + 6 • 8 = 10 – 5 + 48 = 5 + 48 = 53
3) Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать первое и второе правила.
Например,
В числовом выражении 4 арифметических действия: вычитание, деление, сложение и умножение.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим вычитание в скобках, затем деление, потом умножение и сложение.
Полностью пример записываем так:
(25 – 10) : 3 + 6 • 8 = 15 : 3 + 6 • 8 = 5 + 6 • 8 = 5 + 48 = 53
Например,
В числовом выражении 4 арифметических действия: сложение, деление, сложение и деление.
Определим порядок действий и запишем их над арифметическими знаками: сначала производим действия в скобках (деление, затем сложение), затем деление, потом сложение.
Полностью пример записываем так:
42 + 18 : (6 + 12 : 4) = 42 + 18 : (6 + 3) = 42 + 18 : 9 = 42 + 2 = 44
Порядок выполнения действий, правила, примеры
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Решение
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
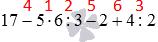
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Решение
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Решение
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Решение
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
Порядок действий в математике
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные операции в математике
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо.
Сначала умножение или сложение? — Умножаем, потом складываем.
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Подставляем полученные значения в исходное выражение:
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!
Правила выполнения математических действий
Основные операции в математике
Основными действиями являются:
Наряду с этими операциями предусмотрены отношения:
Сложение является операцией для объединения пары слагаемых.
Сложение записывают таким образом:
5, 1 — слагаемые, 6 — сумма.
Вычитание — операция, которая является обратным действием сложению.
Записывать вычитание следует таким образом:
10 — уменьшаемое, 1 — вычитаемое, 9 — разность.
При сложении разности в виде 9 и вычитаемого в виде 1 можно получить 10, которое является уменьшаемым. Сложение можно проверить вычитанием:
Умножение является действием в арифметике и имеет вид сокращенной записи сложения идентичных слагаемых.
В данном случае 3 — множимое, 4 — множитель, 12 — произведение.
Множимое и множитель можно поменять местами. При этом произведение не поменяется:
В связи с этим, множитель и множимое являются сомножителями.
Деление — арифметическая операция, которая является обратным действием умножению.
Деление, в том числе для многочленов, записывают таким образом:
При умножении делителя на частное получаем делимое, то есть:
В некоторых уравнениях можно встретить на месте частного не целое число. В таком случае его допустимо записать в виде дроби.
Возведение в степень является действием умножения числа на самого себя несколько раз.
Основанием степени является число, повторяющееся сомножителем конкретное количество раз. Роль показателя степени играет число, указывающее на то количество раз, которое берется одинаковый множитель. Степень — число, являющееся результатом взаимодействия основания и показателя степени.
Здесь 3 является основанием степени, 4 определяется, как показатель степени, 81 называют степенью.
Вторая степень — квадрат, а третья степень — куб. Первая степень числа является самим числом.
В данном случае 81 является подкоренным числом, 4 — показатель корня, 3 — корень.
С целью проверки операции по извлечению корня можно возвести 3 в степень 4, что в результате дает 81:
Квадратный корень — это корень второй степени:
Если предполагается запись квадратного корня, то показатель корня допускается не записывать:
Кубический корень — это корень третьей степени:
Сложение является обратным действием вычитанию, умножение — делению, возведение в степень — извлечению корня, и наоборот.
Порядок вычисления простых выражений
Перед решением простых уравнений полезно ознакомиться с последовательностью действий:
Рассмотреть это правило можно на практике.
Нужно решить письменное уравнение:
В первую очередь следует проверить, есть ли скобки для группировки элементов выражения. Здесь они отсутствуют, как и операции умножения и деления. Тогда можно выполнять действия, руководствуясь стандартным алгоритмом, описанным выше: витаем 2 из 11, складываем остаток с 5, в результате получим 14.
11 – 2 + 5 = 9 + 5 = 14
Скобки в данном примере отсутствуют, но имеются операции деления и умножения. При их обнаружении нужно с помощью правила последовательно выполнять действия, двигаясь слева направо: 10 делим на 2, полученное число умножаем на 7, результат делим на 5.
10 ÷ 2 × 7 ÷ 5 = 5 × 7 ÷ 5 = 35 ÷ 5 = 7
В процессе изучения данной темы, пока опыта еще не достаточно, полезно расставлять над знаками арифметических операций цифры в порядке их выполнения. Такая работа значительно упрощает вычисления и исключает ошибки.
Что такое действия первой и второй ступени
В учебной литературе по математике можно встретить такие понятия, как действие первой и второй ступени:
В том случае, когда в выражении отсутствуют скобки, операции выполняются в следующем порядке:
Порядок вычислений в выражениях со скобками
Наличие в выражении скобок изменяет стандартный алгоритм арифметических операций. Это своеобразный индикатор для действий, которые должны быть выполнены в первую очередь.
В первую очередь следует выполнить операции, заключенные в скобках. При этом важно соблюдать стандартный порядок действий, то есть слева направо умножать и делить, а далее — складывать и вычитать.
Выражения, заключенные в скобках, являются составными компонентами начального выражения. Для таких выражений стандартный алгоритм действий остается без изменений. Рассмотреть вычисления можно на практических примерах.
Так как в выражении есть скобки, в первую очередь нужно выполнить действия в этих скобках:
Руководствуясь стандартным алгоритмом, сначала умножаем, затем — вычитаем:
Перейдем ко второму выражению, заключенному в скобках:
Так как в данном случае имеется лишь вычитание, выполняем действие:
Результаты, которые получили при решении выражений в скобках, следует подставить в начальное выражение:
Сначала нужно умножить, затем поделить, а далее выполнить сложение:
10 + 2 × 8 ÷ 2 = 10 + 16 ÷ 2 = 10 + 8 = 18
Порядок действий в выражениях без скобок
В данном случае присутствуют действия сложения и вычитания, которые следует выполнять по порядку, двигаясь слева направо.
Здесь умножение и деление. Данные арифметические операции также выполняем по порядку, начиная с левой стороны, двигаясь в правую сторону.
Когда выражения содержат операции сложение и вычитание, либо деление и умножение, то вычисления нужно выполнять по порядку слева направо.
Нередко встречаются примеры, где есть сложение и вычитание, а также умножение и деление. Тогда в первую очередь делят и умножают по порядку, а на втором этапе складывают и вычитают также в определенном порядке.
Решение примеров
Согласно стандартному алгоритму, проверяем наличие скобок. Так как скобки имеются, начинаем с них:
Полученный результат следует подставить в исходное выражение:
Скобки отсутствуют, но есть умножение, которое необходимо выполнить в первую очередь:
Подставим результат в начальное выражение:
Решим полученное выражение:
Если сразу обозначить порядок действий, то запись примет вид:


