Прикладная математика и математика в чем разница
Математика – это фундаментальная наука, которая занимается изучением разных структур, их отношений и порядков. Математика, как наука, появилась очень давно, наверное, с возникновением человечества. Уже в раннем палеолите люди были знакомы с основами счета. У людей всегда была необходимость что-то подсчитать или пересчитать. Известно, что для счета люди пользовались и пальцами, и камнями, и палками и различными метками. Историю развития математики отсчитывают именно с того момента, как люди научились считать.
Для того чтобы понять, чем отличается прикладная математика от математики, нужно рассмотреть основные понятия, которыми оперирует одна и вторая наука.
Математика
Если посмотреть определение математики в различных словарях и энциклопедиях, то можно заметить, что единого точного определения математики не существует. Однако мы все интуитивно понимаем, что такое математика. Наилучшее определение было дано, наверное, Бурбаки.
Бурбаки – это псевдоним группы математиков, которые написали серию книг по математике. По определению Бурбаки, математика изучает отношения между какими-то объектами. Каждый объект описывается с точки зрения его количественных характеристик. Сущностью математики является описание некоторого набора абстрактных структур.
Из этого определения становится понятно, чем занимается теоретическая математика. Она должна описать отношения различных структур данных.
Математика делится на элементарную и высшую части. Элементарную математику изучают в школе.
Элементарная математика включает в себя такие разделы, как:
Геометрия
Высшая математика состоит из:
В теоретической математике разработан математический аппарат, основу которого составляют обозначения, аксиомы, утверждения. А на базе уже этого аппарата развивается дальнейшая теория, доказываются теоремы и выводятся определенные правила.
Наука математика
Например, в математическом анализе используются такие понятия, как бесконечно малая величина, дифференциал, функция. Алгебра оперирует понятиями множество, группа, кольцо и т.д. Дифференциальные уравнения работают с производной и интегралом. Таким образом, видно, что теоретическая математика разрабатывает некий понятийный аппарат. Английский математик Годфри Харди говорил, что чистая математика не приносит никакой практической пользы.
Прикладная математика
Прикладная математика является частью математики. Если говорить обычным языком, прикладная математика – это математика, которая используется на практике. Прикладная математика изучает и разрабатывает способы применения теоретической математики в других дисциплинах. Если вернуться к словам математика Харди, то в отличие от чистой математики, прикладная математика приносит практическую польз
Разделы прикладной математики
Предметом исследования прикладной математики является применение теоретических математических методов чистой математики в других науках. Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.
Использование прикладной математики
В физике или химии для проведения каких-либо экспериментов или опытов, не всегда представляется возможным провести испытания на реальном объекте. Поэтому строится его модель. Модель – это уменьшенная или увеличенная копия реального объекта, которая имеет точно такие же свойства.
Модели бывают математическими. Модель может быть создана и на компьютере с помощью графических редакторов. Моделирование разных физических или химических процессов заканчивается решением с использованием численных методов.
Криптография – это наука, которая занимается шифрованием. В шифровании используются различные математические методы и алгоритмы.
Таким образом, из вышеприведенного понятно, что и чистая математика, и прикладная математика использует одни и те же методы. Но чистая математика использует эти методы для дальнейшего развития теории, а прикладная математика использует математические методы и теорию чистой математики для того, чтобы можно было решать реальные задачи в физике, химии, биологии, статистике, экономике и в других науках.
О математике прикладной и чистой
Здесь также можно найти биографические сведения о некоторых цитируемых ученых:
(Д. И. Фонвизин «Недоросль», 1783)
Академик А. Н. Крылов (1863–1945):
«Это может служить отличным пояснением разницы между математикой чистой и прикладной, только здесь не шесть недель, например, теория конических сечений была «существительной», а две тысячи лет, пока Кеплер воспользовался ею для создания точной теории движения небесных тел, а от этой теории Ньютон затем создал механику, служащую основой всей физики и техники.»
(Крылов А. Н. Прикладная математика и техника // Воспоминания и очерки. М.: АН СССР, 1956)
Дж. У. Гиббс (1839–1903):
Математик может говорить, что ему хочется, но физик должен, хотя бы в какой-то мере, быть в здравом рассудке.
Из рассказов академика В. И. Смирнова (1887–1974):
«А знаете у кого я слушал курс теории вероятностей? У самого Андрея Андреевича Маркова (старшего). О, это был человек крутого нрава! Он начал свою первую лекцию так: «Господа! Некто Гильберт недавно выдвинул перед математиками всего мира 23 задачи, объявив их почему-то наиболее важными. И среди них имелось предложение переделать теорию вероятностей на аксиоматической основе. К сожалению, наше математическое общество сочло возможным согласиться с господином Гильбертом и рекомендовало вниманию своих членов все без исключения придуманные им задачи. В знак протеста я немедленно вышел из этого общества!» Здесь Андрей Андреевич медленно обвел глазами аудиторию и, немного помолчав, сказал:»А теперь приступим к делу.».
А знаете у кого я слушал лекции по теории чисел? У самого Успенского! А начал он первую лекцию так: «В последнее время многие математики уделяют серьезное внимание точному определению понятия целого числа. Но, господа, не будем же мы здесь тратить свое время на рассмотрение вопроса, ясного всякой рыночной торговке? И при этом без каких-либо шансов добавить что-либо существенное к тому, что она уже отлично знает!»
(В.В.Новожилов «Воспоминания. В.И.Смирнов» В кн. «Вопросы механики сплошной среды», Л.: Судостроение, 1989. С. 384–385)
Из отзыва академика Л. Д. Ландау (1908–1968) на программу по математике, составленную для одного из физических факультетов:
«При всей важности математики для физиков физика, как известно, нуждается в считающей аналитической математике; математики же, по не понятной мне причине, подсовывают нам в качестве принудительного ассортимента логические упражнения. Мне кажется, что давно пора обучать физиков тому, что они сами считают нужным для себя, а не спасать их души вопреки их собственному желанию. Мне не хочется дискутировать с достойной средневековой схоластики мыслью, что путем изучения ненужных им вещей люди будто бы научаются логически мыслить. Я категорически считаю, что из математики, изучаемой физиками, должны быть полностью изгнаны всякие теоремы существования, слишком строгие доказательства и т.п. Поэтому я не буду отдельно останавливаться на многочисленных пунктах Вашей программы, резко противоречащих этой точке зрения».
Академик В. В. Новожилов (1910–1987):
«Расцвет аксиоматической математики в ХХ в. привел ко все большему углублению различий между мышлениями «чистых» и прикладных математиков, ввиду чего все труднее становится совмещать работу в обоих направлениях. В связи с этим возникли серьезные до сих пор не решенные проблемы в области обучения математике. Испокон веков профессиональных математиков готовят в университетах на соответствующих факультетах. В настоящее время многочисленные университеты страны ежегодно выпускают большую армию математиков, воспитанную, разумеется, в духе наиболее современных идей, т.е. идей стерильной строгости.
. В соответствии с обрисованным положением выпускники-математики в своем большинстве имеют смутные представления о круге интересов деятельности прикладных математиков, в лучшем случае считая, что в современных условиях она сводится к программированию на ЭВМ (руководствуясь при этом, разумеется, только строго обоснованными алгоритмами).
. Чтобы представить себе, насколько это опасно, рассмотрим следующий гипотетический пример. На одном (произвольно выбранном) автомобильном заводе в Детройте ежедневно записывается число машин, выпущенных начиная с первого числа текущего года, а в реке Москве в те же самые дни измеряется и записывается уровень воды. Получаются два ряда величин, между которыми по вполне определенному закону установлено однозначное соответствие, откуда следует, что уровень воды в реке Москве есть функция выпуска автомобилей в Детройте. Не торопитесь смеяться! С точки зрения современной математики преподаватель, который привел бы этот пример для пояснения понятия функции, был бы совершенно прав. С точки зрения прикладного математика (естествоиспытателя, инженера), всегда имеющего дело с причинными связями и подразумевающего под функцией зависимость одной переменной физической величины от другой, этот пример воспринимается как вопиющая нелепость.
Замкнутая в себе стерильная математика — это не только «роскошь», которую может себе позволить цивилизация, но и неизбежное следствие цивилизации. С этой точки зрения борьба с чрезмерным распространением математического формализма среди населения земного шара является проблемой экологической».
Академик В. И. Арнольд:
«Обычное (хотя обычно и скрываемое) мнение как чистых математиков, так и теоретических физиков об «индустриальной и прикладной» математике состоит в том, что это — мафия слабых мыслителей, неспособных произвести никакие важные научные результаты, а просто эксплуатирующих достижения чистых математиков прошлых поколений, что члены этой мафии более заинтересованы в деньгах, чем в науке и безнадежно испорчены.
«Они так скромны, — сказал однажды один чистый математик, — что не надеются добиться чего-либо честным путем; им приходится отделяться от математиков просто для того, чтобы избежать честного соревнования».
Я не думаю, чтобы эта характеристика прикладных математиков была полностью заслуженной. Достижения склонного к бизнесу Галилея вызывают не меньшее восхищение, чем результаты чистого философа Паскаля.
Разница между чистой и прикладной математикой не научная, а лишь социальная. Чистому математику платят за то, чтобы он открывал новые математические факты. Прикладному математику платят за решение вполне определенных задач.
ПРИМЕР. Колумб вначале действовал подобно прикладному ученому, стараясь найти путь в Индию, за что ему и платили. В конце его путешествие напоминало деятельность чистого математика. Заметим, что непосредственная, немедленная польза для испанской экономики от открытий Колумба была гораздо меньшей, чем от каботажных плаваний рядовых капитанов.
. Проблема Ферма тоже была бы прикладной, если бы за ее решение платили. Опасность разделения математики на части хорошо осознавали математики двадцатого века. Герман Вейль писал: «В наше время за душу каждой области математики борются ангел топологии и дьявол абстрактной алгебры».
В первой половине века дьявол побеждал. Вслед за Лагранжем, изгнавшим из математики чертежи, пришли алгебраисты и аксиоматизаторы — сперва Гильберт, затем Бурбаки.
. Гильберт провозгласил демократический принцип, по которому всякая система аксиом имеет равное право быть исследованной, а значение математического достижения определяется лишь его трудностью, как в альпинизме. Результатом явился развод «чистой» математики со всеми науками, преступная по отношению к обучаемым система обучения математике и образ математики в общественном мнении как опасной паразитической секты на теле науки и техники, состоящей из жрецов умирающей религии, вроде друидов.
. Мстя за унижения, перенесенные в школе, правители большинства стран, подобно свиньям под дубом, предпринимают теперь, после уменьшения военного противостояния, усилия для изничтожения математики, особенно «чистой». Правительство США недавно выяснило, что 85% имеющихся и обучающихся математиков стране не нужны. Без звездных войн не нужны ни суперколайдеры, ни математики. Обсуждаются различные проекты, как сократить число математиков в семь раз. Американские специалисты считают, что на это потребуется лет десять.
К сожалению, нельзя не признать, что «чистые» математики своими руками сделали все для того, чтобы создать описанное общественное мнение. Аксиоматически-дедуктивный метод, приведший к изгнанию всех примеров (а особенно мотивировок вводимых определений) в преподавание математики на всех уровнях прежде всего ответственен за это.»
(В. И. Арнольд. Топологические проблемы теории распространения волн // Успехи мат. наук. 1996. Т. 51, вып. 1 (307). С. 3-5)
Академик В. В. Новожилов:
«Достоинство теоретика состоит в умении, абстрагируясь от ряда деталей, создавать простые математические модели сложных явлений. Он должен выделить «чистый» закон из опыта, «загрязненного» побочными эффектами, как это сделал, например, Галилей, сформулировав закон инерции. Конструктор, наоборот, должен быть предельно конкретен, энциклопедичен в своих знаниях, должен хранить в них опыт, накопленный предыдущей инженерной практикой, опыт, который зачастую не может быть облечен в теоретическую форму. При проектировании сложных конструкций нет ничего второстепенного. В технике крупные неудачи чаще всего встречаются из-за упущений в мелочах.
Другим примером, показывающим, что склонность к абстрагированию не может привести ни к чему хорошему, является деятельность хирургов. Один опытный хирург говорил мне, что, хотя операция аппендицита и считается простой, пока не прооперируешь сто больных, не увидишь случая, похожего на один из предыдущих. Всякий раз приходится приспосабливаться к случайной обстановке, быть готовым к неожиданностям.
Таким образом, конструкторы и хирурги по складу своего мышления ближе, чем, скажем, конструкторы и современные математики-алгебраисты, являющиеся на сегодня наиболее яркими представителями абстрактного, формально-логического мышления. И если бы конструктору предоставили на выбор право взять себе в подручные хирурга или алгебраиста, я бы на его месте выбрал первого: благодаря одинаковому складу мышления им гораздо легче достигнуть взаимопонимания.
Разумеется, деление людей на «абстрактных» и «конкретных» — само по себе абстрактно. Каждый индивидуум наделен способностью и к конкретному и к абстрактному мышлению. Можно говорить о преобладании у разных людей той или иной его формы.
Существует предание, что один из учеников великого математика нашего века Гильберта к общему удивлению вдруг стал писателем.
«Но это же очень просто, — заметил по этому поводу Гильберт, — для математика у него не хватало воображения, в то время как его хватило на романы»
Реплику Гильберта иногда расценивают как чуть ли не доказательство интеллектуального превосходства математической деятельности. Жаль, однако, что Гильберт не попытался написать хотя бы один рассказ. Он тогда бы убедился, что если у его ученика не хватало того вида воображения, который нужен для математика, то у него самого полностью отсутствует вид воображения, который нужен писателю.
. Гаусс называл математику «царицей наук», а ее раздел «Теория чисел» «царицей математики». Но ведь прикладная ценность большинства результатов теории чисел незначительна! Что бы выиграла техника, если бы наконец была доказана теорема Ферма, являющаяся перчаткой, брошенной в лицо математикам триста лет назад? Да ровно ничего! Но нельзя оспаривать, что это было бы одной из великих побед ума, а вместе с тем и всей культуры. Поэтому инженеры и физики не вправе вмешиваться в дела математиков, учить их, что для них важно, а что нет, и как им подготавливать свою научную смену. В этом мы не компетентны. Но мы вправе ожидать и от них должного понимания наших интересов в области преподавания математики инженерам и здесь, несомненно, имеем право решающего голоса.»
(В.В.Новожилов. О принципах преподавания математики школьникам и инженерам // Вопросы механики сплошной среды. Л.: Судостроение, 1989)
Аристотель (384-322 до н.э.)
А математической точности нужно требовать не для всех предметов, а лишь для нематериальных. Вот почему этот способ не подходит для рассуждающего о природе, ибо вся природа, можно сказать, материальна.
(Аристотель «Метафизика») Писатель В.Конецкий (1929–2002):
«Бывший министр просвещения и науки Англии профессор Бертрам Боуден заметил, что если закон, которому подчиняется рост числа ученых в наше время, будет действовать в течение еще двух столетий, то все мужчины, женщины и дети, все собаки, лошади и коровы будут учеными. К тому же времени у человечества не станет денег на поиск все новой и новой информации. Вот тогда-то в цену и войдет не талант искателя новизны, а способность из гор старых знаний, путем ассоциаций и неожиданных состыкований их, высекать искры постижений. И появится профессия «ассоциантов». Людей дилетантского знания из множества областей. И это неизбежно. И уже сегодня надо отбирать таких людей и давать им свободу шататься с факультета на факультет, продлив им студенческую стипендию до самой смерти.
О, это будут люди самой странной профессии во Вселенной. Им будет разрешено глухой ночью бродить по Эрмитажу или Лувру. И они будут слушать мраморное дыхание античных богинь в тишине раннего утра. И у них будет допуск в жилище молодых зверят во все зоопарки. Их будут приглашать в запретные уголки ботанических садов в моменты, когда раскрываются самые чудесные цветы самых чудесных кактусов. И они будут летать первыми на другие планеты без всяких специальных целей — только ради радости возвращения на Землю. С ними будут кокетничать и лукавить самые обворожительные девушки. И даже самые застенчивые музыканты будут разрешать им сидеть в пустом репетиционном зале, когда нежная музыка еще только в бутонах и непосвященным нельзя глядеть на нее».
(В.Конецкий «На околонаучной параболе»)
Разница между математикой и прикладной математикой
Математика против прикладной математики Математика впервые возникла из повседневной необходимости древних людей считать. Торговля со ссылкой на время и измерение урожая или земли требовали количества
Содержание:
Математика против прикладной математики
Математика впервые возникла из повседневной необходимости древних людей считать. Торговля со ссылкой на время и измерение урожая или земли требовали количества и стоимости для их представления. Поиск творческих путей решения вышеупомянутых задач привел к основному виду математики, который привел к натуральным числам и их вычислениям. Дальнейшее развитие этой области привело к введению нулевых, а затем отрицательных чисел.
За тысячи лет развития математика оставила фундаментальную форму вычислений и превратилась в более абстрактное изучение математических сущностей. Наиболее интересным аспектом этого исследования является то, что эти концепции могут быть использованы в физическом мире для предсказаний и для бесчисленного множества других применений. Следовательно, математика занимает очень важное место в любой развитой цивилизации мира.
Абстрактное исследование математических сущностей можно рассматривать как чистую математику, в то время как методы, описывающие их применение для конкретных случаев в реальном мире, можно рассматривать как прикладную математику.
Математика
Математика подчиняется логике; поддержанные теорией множеств, теорией категорий и теорией вычислений, придают структуру пониманию и исследованию математических понятий.
Геометрия исследует свойства и объекты в пространстве. Дифференциальная геометрия и топология позволяют лучше понять пространство. Тригонометрия, фрактальная геометрия и теория меры также включают изучение пространства в общем и абстрактном смысле.
Это изменение является основным интересом таких областей, как исчисление, векторное исчисление, дифференциальные уравнения, реальный анализ и комплексный анализ, а также теория хаоса.
Прикладная математика
Прикладная математика фокусируется на математических методах, используемых в реальных приложениях в области инженерии, естественных наук, экономики, финансов и многих других предметов.
В чем разница между математикой и прикладной математикой?
• Математика основана на математической логике, и некоторые фундаментальные концепции описываются с помощью теории множеств и теории категорий.
• Исчисление, дифференциальные уравнения, алгебра и т. Д. Предоставляют средства абстрактного понимания структуры и свойств количества, структуры, пространства и изменений.
• Прикладная математика описывает методы, с помощью которых математические концепции могут применяться в реальных ситуациях. Вычислительные науки, такие как оптимизация и численный анализ, являются областями прикладной математики.
Прикладная или фундаментальная: какой считают в мире математику
Можно ли считать математику фундаментальной наукой или это всего лишь инструмент, как писал советский математик Колмогоров, на службе у естественных наук — этот вопрос остается открытым. Даже сами математики отказываются однозначно отвечать на него. Методист по математике Университета Иннополис Дмитрий Бебчук рассказал на фестивале науки и технологии «ПРОСТО», организованном российским ИТ-вузом, о том, какие изобретения человечества были бы невозможны без математики и почему математизирование — это процесс творческий, не требующий никаких практических целей.
Читайте «Хайтек» в
Наука о структурах или просто расчеты?
« Британника» говорит, что математика — это наука о структурах, порядках и отношениях, возникшая из элементарных практик подсчета, измерения и описания форм объектов. Она строится на логических рассуждениях и количественных расчетах. Группа французских математиков, которые взяли себе в 1935 году коллективный псевдоним Никола Бурбаки, предложила такое определение: математика — это наука об отношениях между объектами, о которых ничего не известно, кроме их свойств. именно ими объекты и описываются. Может возникнуть двоякое впечатление. С одной стороны, у нас есть конструктивное определение математики, а с другой, математика — это когда «взяли что-то и посчитали». Этот своеобразный конфликт выразился в том числе в установлении теории множеств. Есть аксиоматика Сернела Френкеля, которая являет собой конструктивный подход к теории множеств, но существуют и альтернативы. Это всё возникло из-за парадокса Рассела.
Парадокс Рассела — открытый в 1901 году Бертраном Расселом теоретико-множественный парадокс (антиномия), демонстрирующий противоречивость логической системы Фреге, являвшейся ранней попыткой формализации наивной теории множеств Георга Кантора.
Парадокс можно описать следующим образом. Условимся называть множество «обычным», если оно не является своим собственным элементом. Например, множество всех людей является «обычным», так как само множество — не человек. Примером «необычного» множества является множество всех множеств, так как оно само является множеством, а, следовательно, само является собственным элементом.
Система аксиом Цермело — Френкеля (ZF) — наиболее широко используемый вариант аксиоматической теории множеств. Сформулирована Эрнстом Цермело в 1908 году для преодоления парадоксов теории множеств, а затем была уточнена Абрахамом Френкелем в 1921 году. Система аксиом записана на языке логики первого порядка.
Я попытаюсь вам доказать, что математика — это фундаментальная наука. Фундаментальная наука должна обладать следующими свойствами: ее результаты должны быть универсальны; в ее задачи не должна входить изначально практическая реализация полученных результатов; и она позволяет нам получать новые знания о природе, то есть иметь предсказательную силу.
В универсальности результатов математики сомнений нет. Это самый легкий пункт, поэтому он стоит первым. Действительно, даже на уровне «дважды два — четыре»: в любое время и на любом континенте это будет, конечно же, четыре.
Как из чистых идей родились практические инструменты
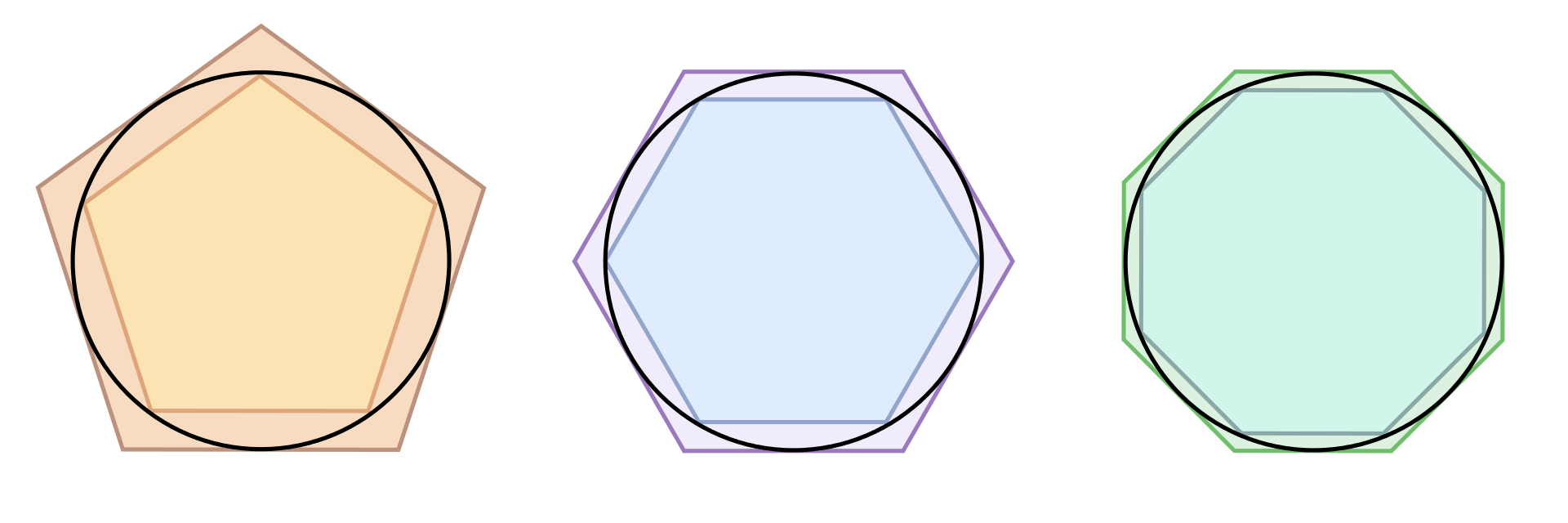
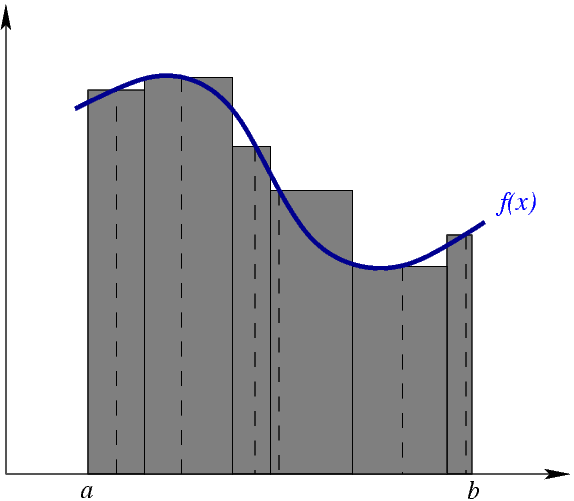
Существуют четыре области математики, которые развились из совершенно абстрактной идеи. Во-первых, анализ бесконечно малых, то, что сейчас называют математическим анализом. Началось всё с того, что предположительно Антифон в V веке до нашей эры предложил метод исчерпывания. Он и сейчас так называется. С помощью этого метода можно находить площадь фигур, границы которых — не отрезки. Например, площадь круга. Если есть круг, то его можно заключить, например, в пятиугольник, а также вписать в него пятиугольник. Площадь круга получится чем-то средним между ними. Если заменить пятиугольник на шести-, семи- и восьмиугольник, то точность приближения возрастет. Чем больше количество сторон у нашего вот многоугольника, который вписан и описан около круга, тем лучше оказывается наше приближение.
Но площадь круга пропорциональна квадрату радиуса, а коэффициент пропорциональности — это какое-то число. Были предложены оценки этого числа: например, Архимед предположил, что это примерно 22/7, эта оценка позволяет нам получить точность до двух знаков после десятичной запятой. А пресловутый Цзу Чунжи уже предложил оценку намного лучше: 355/113, уже шесть знаков после запятой. В конце концов, было доказано, что пи — это число иррациональное и даже трансцендентное, то есть не является алгебраическим числом.
Цзу Чунжи — китайский математик и астроном. Как астроном определил сидерические периоды обращения планет Солнечной системы с высокой точностью. Разработал новый календарь с учетом явления прецессии. Как математик первым в мире рассчитал число пи с точностью до седьмого знака после запятой, дав его значение между 3,1415926 и 3,1415927; более точное значение было вычислено лишь тысячу лет спустя.
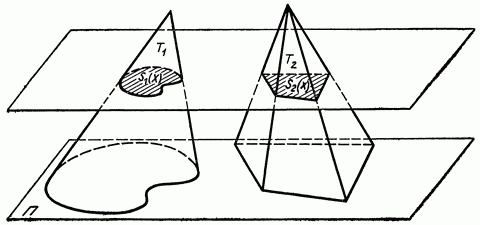
Принцип Кавальери очень прост: если у вас есть два объемных тела одинаковой высоты и на каждом уровне площади иссечений одинаковы, то и объемы этих тел одинаковы. Такой принцип подходит для нахождения объемов тел, у которых грани необязательно плоские. Например, конус. Из таких совершенно теоретических подходов к XVII веку уже развивается дифференциальное и интегральное исчисление, у истоков которого стоят двое ученых — Ньютон и Лейбниц, которые примерно одновременно развивали эту область. Практическое применение их работ сегодня: поиск длины кривой и касательной к сфере, дивергенции, роторы и даже двумерное нормальное распределение, благодаря которому можно искать вероятности сложноконструируемых событий.
Бонавентура Кавальери — итальянский математик, предтеча математического анализа, наиболее яркий и влиятельный представитель «геометрии неделимых». Выдвинутые им принципы и методы позволили еще до открытия математического анализа успешно решить множество задач аналитического характера.
В XVI веке Джероламо Кардано ввел понятие комплексного числа. В его трудах комплексные числа описаны как совершенно утонченные и бесполезные структуры, утонченные — это позитивная характеристика, а бесполезные — ну мы понимаем. Он не видел им совершенно никакого применения, но, тем не менее, пытался развивать эту теорию. Уже потом стало ясно, что это полезный инструмент для многих областей. Альберт Эйнштейн согласился бы. В качестве примеров — расчёт электрических цепей переменного тока, который делается гораздо проще с применением комплексно-значимых функций. Всяческие теоремы о распределении простых чисел — небезызвестная дзета-функция Римана и теорема, связанная с ней, гипотеза, на самом деле, потому что она еще не доказана — это одна из семи проблем тысячелетия. Гиперкомплексные числа, так называемые кватернионы, нашли свое применение в позиционировании. Тут меня поймут робототехники. Когда мы определяем или задаем положение трехмерного объекта в пространстве, то кватернионы исключительно полезны. А обойтись без выхода в это гиперкомплексное пространство нам уже тяжелее.
Джероламо Кардано — итальянский математик, инженер, философ, врач и астролог. В его честь названы открытые Сципионом дель Ферро формулы решения кубического уравнения (Кардано был их первым публикатором), карданов подвес, карданный вал и решетка Кардано.
Кватернионы — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Предложены Уильямом Гамильтоном в 1843 году.
Некоторые алгоритмы шифрования основаны на свойствах эллиптических кривых, а, точнее, на их алгебраических свойствах. Но всё началось с того, что Диофант Александрийский в III веке нашей эры пытался найти решение этого уравнения: y*(6-y)=x3-x. В конце XVII — начале XVIII века Ньютон тоже пытался его решить. Все вылилось в целую теорию, которая позволяет нам достаточно быстро зашифровать данные, с тем, чтобы их расшифровка требовала существенно больше времени. То есть мы получаем криптографически такой механизм — алгоритм.
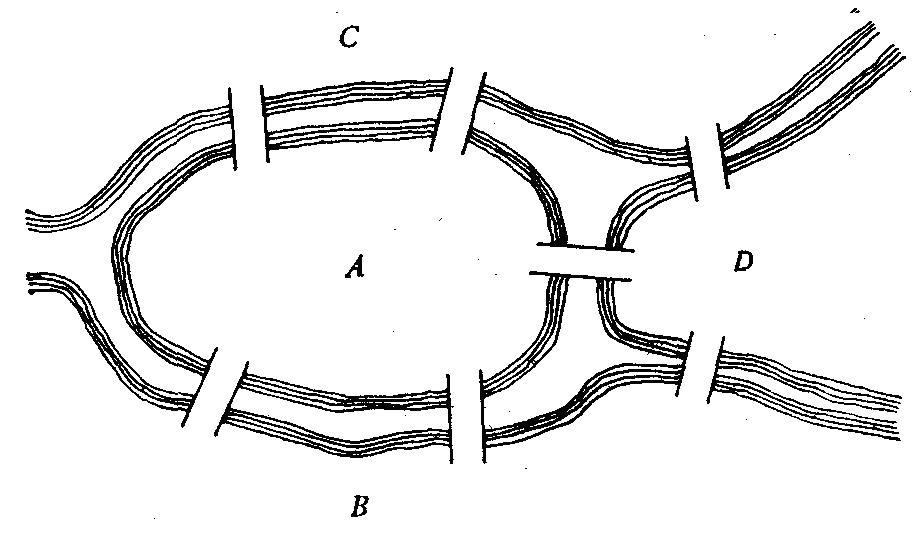
Задачу мостов Эйлера: существует ли маршрут, чтобы обойти каждый мост Кенигсберга только по одному разу, — сегодня может решить почти любой олимпиадник. Этот вопрос XVIII века, тогда еще практически неприменимый, породил целую область математики — топологию. Сегодня она применяется, например, в робототехнике. У манипулятора есть конфигурационное пространство. Например, у двухзвенного манипулятора — это тор. Но тор — это определенный топологический объект: если мы возьмем две точки на торе, то сможем сказать про траекторию передвижения между этими двумя точками, про минимальность и так далее. То есть появляется целая область для анализа. А если манипулятор трехзвенный, то и поверхность становится значительно сложнее, а задача по нахождению какого-то оптимального пути или даже просто нахождению пути — на порядки. Тут без топологии уже не обойтись.
Анализ бесконечно малых, топология, эллиптические кривые — все это доказывает то, что в развитие этих областей было вовлечено много людей. А после XVIII века математика уже становится профессиональный наукой, то есть человек со стороны практически не имеет шансов добиться в ней значимых на мировом уровне успехов. Второй тезис, получается, доказан. Эти люди занимались математикой всю жизнь, не надеясь на то, что их конкретные результаты будут практически применимыми.
Как способ описать природу
Пресловутый Бозон Хиггса, который, конечно, прежде чем был обнаружен и зафиксирован, сначала был рассчитан. То есть была целая теория, основанная на расчетах. Теория, согласно которой такая частица должна существовать и должна обладать определенными свойствами. Это доказывает, что математика позволяет получать новые знания о природе. Вернемся к самому началу: что математика — это наука о неких структурах, у которых мы знаем только свойства, а потом уже смотрим, а что же из этого получается. Бозон Хиггса, который тогда еще не знали, но уже по предположениям ученых должен был обладать определенными свойствами.
Второй пример — девятая планета. Российский ученый Батыгин, который сейчас преподает в США, сначала вычислил орбиту девятой планеты, прежде чем ее обнаружили. То есть, согласно каким-то расчетам, эта планета должна была существовать, а потом она уже была обнаружена в расчетной точке.
Получается, что математика — фундаментальная наука. Но многие скажут, что математика — это просто дисциплина на службе естественных наук, и отчасти они будут правы. И с ними согласился бы даже Колмогоров, который в предисловии к книге Куранта и Роббинса так и сказал, что математика неотделима от ее практических применений.
Андрей Колмогоров — советский математик, один из основоположников современной теории вероятностей, им получены фундаментальные результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории функций и в ряде других областей математики и ее приложений.
Рихард Курант — немецкий и американский математик, педагог и научный организатор. Известен как автор классической популярной книги по математике «Что такое математика?», а также как один из авторов критерия Куранта — Фридрихса — Леви.
Герберт Роббинс — американский математик и статистик. Его именем названы лемма Роббинса, алгебра Роббинса, теорема Роббинса и другие термины.
Вейль говорит о том, что вопрос об основаниях математики и о том, что в конечном счете она собой представляет, остается открытым. И неизвестно такого направления, которое позволит в конце концов найти окончательный ответ на этот вопрос. Можно ли ожидать, что он когда-нибудь будет получен и признан всеми математиками? Вейль указывает на то, что сам процесс изучения математики, математизирование — это творческий процесс, когда люди, не надеясь на практическое применение их результатов, результатов их работы, просто занимаются этим процессом. Но а то, что он описывает мир, надеюсь, я вас убедил, тут сомнений уже нет. Математика действительно описывает мир, и нет естественной науки, которая не пользовалась бы математическим аппаратом. В современном мире и общественные науки, в том числе социология, пользуются математическими методами как методами для исследования.
Андре Вейль — французский математик, внесший значительный вклад в алгебраическую геометрию и топологию, член группы Бурбаки. Важнейшие труды в области алгебраической геометрии, которую сумел обосновать с нужным уровнем строгости, получил важные результаты в функциональном анализе, в частности в теории меры и интегрирования в топологических группах и теории чисел, к которой применил аппарат гомологической алгебры и функционального анализа.