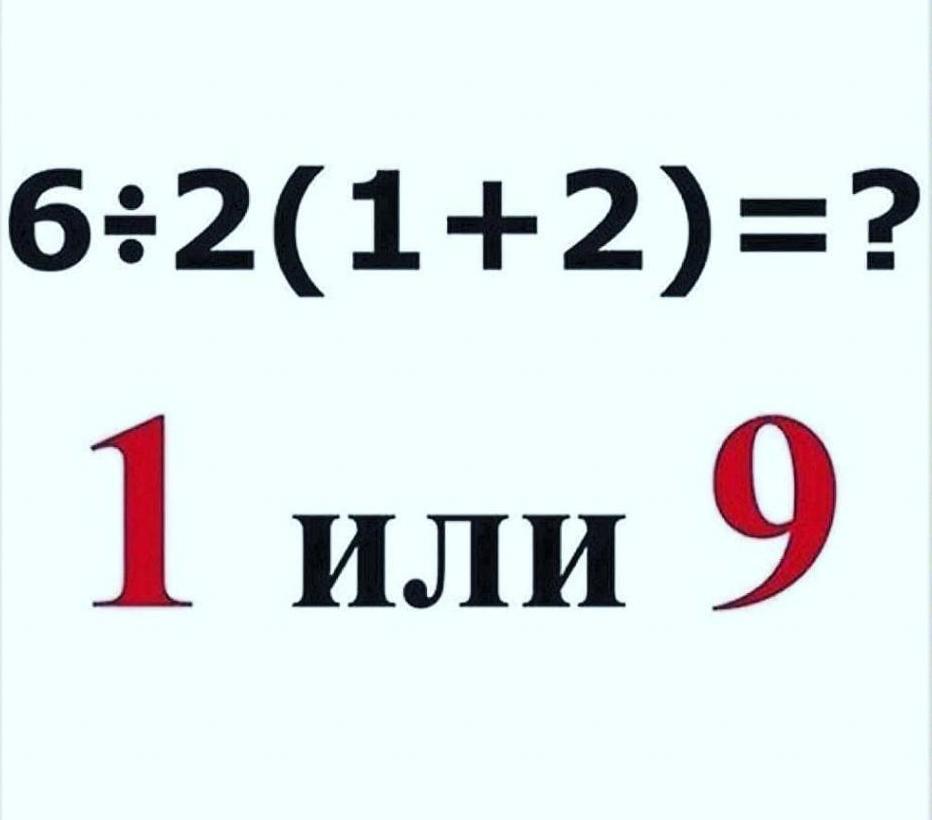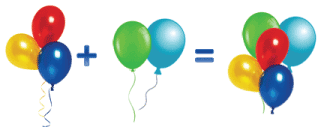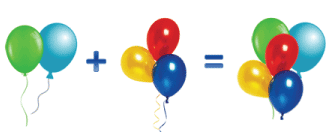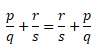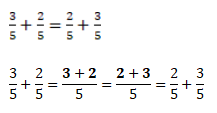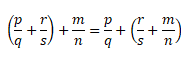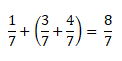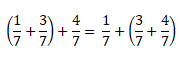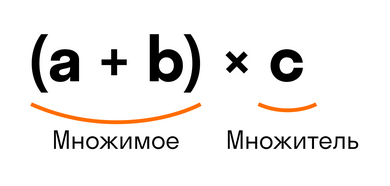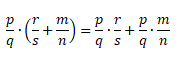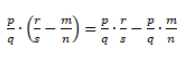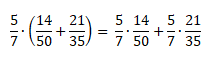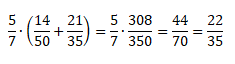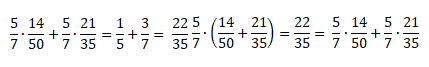Правильное сложение ряд чего либо
Правильно сложенный ряд чего-либо
Последняя бука буква «ь»
Ответ на вопрос «Правильно сложенный ряд чего-либо «, 7 (семь) букв:
штабель
Альтернативные вопросы в кроссвордах для слова штабель
Определение слова штабель в словарях
Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
штабеля, мн. штабели-штабеля, м. (нем. Stapel). Ровно и в правильной форме сложенный ряд чего-н. (преимущ. строительного материала). Доски в штабелях. Штабель дров.
Примеры употребления слова штабель в литературе.
На первый случай предложил товарищам командирам оставить его и Бабенко с Фефеловым на пристани дежурить, иначе штабеля леса да и землянку бердские граждане за ночь растащут на дрова.
Он сел на пол рядом с раненым, который теперь был в полусознании от шока, и стал оглядывать стоявшие вокруг штабеля ящиков, длинные темные проходы между ними, беловатый отблеск дневного света из зарешеченных, узких, как щели, окон в стене фасада, белые полосы селитры на потолке, следы сапог рабочих и колес тележек на пыльном цементном полу.
Кучи гравия, штабеля бетонных блоков, бетономешалки, непосаженые деревья с корнями в мешках.
Владелец верфи мистер Паттерсон, сопровождавший своего заказчика, сэра Фредрика Райленда, шагал по горам стружки, щепы и опилок, лавируя между штабелями бревен и бухтами канатов.
Как самый страшный кошмар детства вспоминал Климчак этот переезд: битком набитый запертый снаружи вагон, где люди оправлялись на глазах друг у друга, где трупы умерших оттаскивали в угол и складывали штабелями, где женщины рожали детей прямо на загаженном полу.
Источник: библиотека Максима Мошкова
Словари
1. Класть все в одно место.
отт. Укладывать в определенном порядке.
2. Собирать, составлять что-либо целое из отдельных, разрозненных частей, элементов.
3. Строить, возводить путем кладки.
4. Придавать складному предмету компактный вид, сближая его отдельные подвижные части.
5. Сгибая, складывая, придавать чему-либо определенное положение.
II несов. перех. разг.
1. Прибавлять одно число к другому, производя сложение.
Сочинять (стихи, песни и т.п.).
Морфология: я скла́дываю, ты скла́дываешь, он/она/оно скла́дывает, мы скла́дываем, вы скла́дываете, они скла́дывают, скла́дывай, скла́дывайте, скла́дывал, скла́дывала, скла́дывало, скла́дывали, скла́дывающий, скла́дываемый, скла́дывавший, скла́дывая; св. сложи́ть; сущ., с. скла́дывание
1. Если кто-либо складывает что-либо во что-либо, то это означает, что этот человек формирует из какого-то материала, каких-либо вещей удобное для хранения сооружение.
Складывать книги стопкой. | св.
Складывать дрова в поленницу. | св.
Сложить сено в копны, в стога.
2. Если кто-либо складывает что-либо куда-либо, то это означает, что этот человек помещает что-либо в каком-либо месте.
Складывайте вещи в передней. | Складывать бельё в шкаф. | св.
Сложить спички в коробок.
3. Если кто-либо складывает что-либо, то это означает, что этот человек упаковывает во что-либо вещи для отъезда.
Складывать чемодан. | Складывать пожитки.
4. Если кто-либо складывает цифры, то это означает, что этот человек прибавляет одно число к другому, производит операцию математического сложения.
Складывать два и пять. | Научиться складывать в уме. | св.
Сложить несколько трёхзначных чисел.
5. Если кто-либо складывает какую-либо конструкцию, то это означает, что этот человек строит что-либо из кирпичей, камней и т. п.
Складывать фундамент из камней. | Сложить стену из кирпича. | Сложить печку.
6. Если кто-либо складывает ткань, бумагу и т. п., то это означает, что этот человек придаёт им более компактную форму.
Складывать салфетку. | св.
Сложить газету. | Складывать лист бумаги пополам. | Сложить верёвку вдвое. | Аккуратно сложив пляжное полотенце, я взял его под мышку и пошёл к морю.
7. Если кто-либо складывает что-либо, то это означает, что этот человек переводит какой-либо объект, предмет из функционального состояния в сложенное, компактное.
8. Если кто-либо складывает губы, руки, ноги, то это означает, что этот человек придаёт им какое-либо положение, вид.
Складывать губы в улыбку. | Складывать ноги крестом. | св.
Сложить руки на груди, за спиной, на коленях. | Сложить ладони рупором. | Костя сложил ладонь трубочкой и, приставив её к уху старшины, шепнул ему что-то.
9. Если кто-либо молитвенно (с мольбой) складывает руки, то это означает, что этот человек соединяет ладони двух согнутых в локтях рук.
СКЛА́ДЫВАТЬ, складываю, складываешь. несовер. к сложить в 1, 2, 4, 5, 6 и 8 знач. и к скласть.
| * освобождать от чего, облегчать. Склади (либо сложи) дрова с печи, жарко, не закурились бы. Склал (сложил) ношу с плеч. С Ивана недоимку складывают, слагают. Складывать вину на кого, сваливать. Складывать пиво, квас, вологод. спускать и сливать в бочонки, лагуны.
| От класть, строить каменное: по(вы, со)строить (складывать и сложить не употр.). Дом под окна склали, вышли кладкою до окон. Скласть печь, скласть трубу, лежанку.
| Скласть песню, сказку, южн., зап., новг., олон. сложить, сочинить, выдумать складно или нескладно.
| Свертывать, сгибать. Прачка белье складывает. Склади хорошенько боры, сборки, собери. Сложи, да убери платье. Лист складен вчетверо, сложен, перегнут.
| На счетах легче складывается, безличн.
| Мы складываемся, сложились, склались на братское пиво.
| Складется ли все сено на сеновал? уложится, пойдет ли.
| Лошадь не склалась (не сложилась), она еще складывается, молода, мужает, принимает склад, стати. Скласться в дорогу, архан. уложиться, собраться. Складывание, складание ср., ·длит. складение (сложение) ·окончат. склад муж. складка жен., ·длит. действие по гл.
| Склад, место, где что-либо складывается;
| вещи, товар, сложенный где в запас, на сохранение;
| ·стар. сходбище, собрание? кажется, складчина, пир по складке. Складов пировых не твори.
| ·стар., зап. договор, условие, сделка, обоюдное согласие. А тот склад держати на обе стороны у Полоцку и в Ризе.
| Строй, стройность, связь, смысл или толк в речи. Красно говорит, а складу мало, толку. Складно говорено, дай Бог сделано! Ни складу, ни ладу. Слов много, да складу нет. В голове нет складу. Склад тут может означать и слог речи, и ход мыслей, грамматический и логический склад. Склад дороже песни, напева.
| То же, говорят о музыке, последовательность звуков, образуюших напев. Строй лучше песни, стройность, складность звуков; склад лучше песни, смысл Словарь Академии
| Складка, сбор или общий внос чего. У нас склад идет, на выкуп должника.
| Складка, сгиб, морщина, бора, перелом или перегнутое место ткани, кожи, бумага. Складки в одеже, боры. * Загни складку, припомни это.
| Склад, место или самые вещи, сложенные где.
| Складка (денег), скидка, складчина, общий, добровольный внос или сбор, на какое-либо дело; также общий внос по мирскому приговору.
| Сказка складка, а песня быль, выдумка, сочинение. Складка или склад ума, образ, род, вид, ход мыслей или способ разуметь и объясняться. Склад и складица, стать, стройность, красота;
| Складной истиник (капитал), сложившихся промышлеников, складочный, составленный складкою. Складочные рекрутские деньги. Складная грамата, ·стар. разрывная, слагающая все прежние дружеские, мирные условия, объявление войны. Складень муж. складня жен., ряз., тамб. складни муж., мн. две равные деревянные чашки, с закрайками, служащие друг другу покрышкой; иногда их бывает несколько пар, вкладываемых одна в другую; делаются в Семеновском уезде Нижегородской губернии.
| Складень, гривна, род ожерелья с камнями, как борок или монисто, но не низанное, а сборное, на цепочках.
| Складень, двустворчатая ракушка.
| Складни, олон. род складных, попарно, оладьев.
С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.
Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.
Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.
Скобки
Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).
Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.
Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.
(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2
Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.
«Вишенка на торте»
И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:
Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».
«Совсем вишня»
От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.
6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
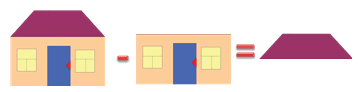
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Законы математики
Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения
От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:
m + n = n + m
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:
Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения
От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения
Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.
Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
c * (a + b) = c * a + c * b
Пример 1
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?
Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?
Задание 8. Верно ли равенство: 8 * 5 = 49?