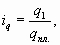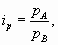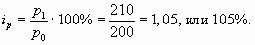построение индексов в статистике

СТАТИСТИЧЕСКИЕ ИНДЕКСЫ

Поможем написать любую работу на аналогичную тему

Само слово «индекс» (index) означает показатель. Обычно этот термин используется для некоторой обобщающей характеристики изменений. Например, индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т.д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.

В практике статистики индексы, наряду со средними величинами, являются наиболее распространенными статистическими показателями. Но индексы имеют три принципиальных отличия.

Во-первых, индексы позволяют измерить изменение сложных явлений (неоднородных статистических совокупностей). Например, нужно определить, как изменились за год расходы жителей г. Луганска на городской транспорт. Для ответа на этот вопрос необходимо знать численность пассажиров, перевезенных за год каждым видом транспорта, рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия – в случае использования среднемесячной численности) и полученные величины просуммировать. То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто средние двух чисел, как при расчете, например, темпов динамики или приростов, а получение и сравнение некоторых агрегатированных величин.

Во-вторых, индексы позволяют проанализировать изменения – выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров, изменения тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта.

В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в Украине в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в Украине и в развитых странах Запада, Востока. А также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое.

Существует множество определений индекса.

Индекс – это показатель сравнений двух состояний одного и того же социально-экономического явления и представляет собой относительную величину, получаемую в результате сопоставления уровней сложных явлений во времени, в пространстве или с планом.

Индекс – это показатель, который сочетает в себе качества средних и относительных величин одновременно Обычно их применяют для характеристики сложных совокупностей единиц наблюдения, то есть состоящих из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости. Например, в магазине ассортимент товаров состоит из разновидностей, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, консервы – в банках, торты – в штуках, макароны – в пачках и т.д. Для определения общего объема реализации продуктов суммировать данные разнородные товары в натуральных единицах их учета, просто, нельзя, так как результат будет бессмысленным. Для получения обобщающих показателей в сложных статистических совокупностях необходимо применять индексный метод.

Индексный метод представляет собой совокупность приемов, которая исторически возникла для измерения динамики социально-экономических явлений. Это сравнительно молодой метод в статистике. В простейшей форме его стали применять более 100 лет тому назад, но по-настоящему этот метод начал развиваться значительно позднее, когда появились большие теоретические работы и практические исследования в этой области.

Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.

В зависимости от степени охвата и характера подвергнутых обобщению единиц изучаемой совокупности все индексы, употребляемые в статистике, делятся на два класса: индивидуальные (элементарные) и общие (сложные).

Индивидуальные индексы – это относительные числа, характеризующие изменения во времени показателей, относящихся к однородному объекту (к одной статистической совокупности), или изменения во времени показатели одновременно существующих однородных объектов (изменения уровней однотипных явлений). Индивидуальные индексы вычисляются просто. Если, например, требуется показать динамику цены или производительности труда, урожайности пшеницы или любой другой культуры с помощью индивидуальных индексов, то берут величину текущего периода и делят ее на величину сравниваемого периода.

Общие индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц сложной статистической совокупности или изменение сложных общественных явлений во времени.

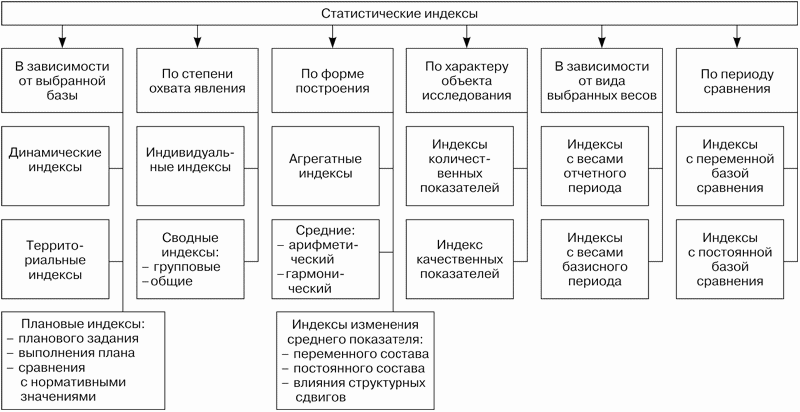
Рис. 13.1. Классификация статистических индексов

Общие индексы подразделяются на индексы объемных и качественных показателей.

К объемным показателям относятся:

— физический объем продукции (обозначается буквой ). Выражается в натуральных единицах объема: кг, литры, метры, мешки, банки, ящики;

— объем продукции или услуг (товарооборот), выраженный в стоимостной форме (обозначается буквами ). Выражается в денежной форме: грн., доллар.

К качественным показателям относятся:

— цена продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;

— себестоимость продукции или услуг (обозначается буквой ). Выражается в денежной форме: грн., доллар;

— затраты на производство продукции (обозначается буквами ). Выражается в денежной форме: грн., доллар.

При вычислении индексов различают сравниваемый уровень (отчетный период), и уровень, с которым производится сравнение, называемый базисным. Если показатель относится к сравниваемому (отчетному) уровню, то индексируемой величине присваивается символ «1» (например, – цена товара за отчетный период), а если показатель относится к базисному периоду, то индексируемой величине присваивается символ «0» (например, — объем продукции за базисный период).

Выбор базы сравнения определяется целью исследований. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком-либо периоде, предшествующем отношению. При этом возможны два способа расчета индексов – цепной и базисный.

Цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.

Базисные индексы получают сопоставлением текущих уровней с уровнем периода, принятого за базу сравнения, т.е. база сравнения остается неизменной.

При использовании индексов как показателей выполнения плана, за базу сравнения принимаются плановые показатели.

В статистике индивидуальные индексы принято обозначать буквой «», а общие индексы – буквой «».

Рассмотрим порядок вычисления индивидуальных индексов. Как уже отмечалось, индивидуальные индексы определяются как отношение уровня исследуемого показателя за отчетный период к уровню того же показателя за базисный период. При этом основным элементом индексного отношения является индексируемая величина, под которой понимается значение показателя за отчетный период. Ее всегда записывают в числителе индексного отношения.

Индивидуальные индексы объема реализации или производства товаров определяют по формуле:

(13.1)

где – индивидуальный индекс объема продукции;

– объем продукции в текущем (отчетном) периоде;

– объем продукции в базисном периоде.

Индивидуальные индексы цены продукции или услуг определяются по формуле:

(13.2)

где – индивидуальный индекс цены продукции;

и – цена продукции в текущем (отчетном) и базисном периодах;

Индивидуальный индекс себестоимости продукции определяется по формуле:

(13.3)

где – индивидуальный индекс себестоимости продукции;

и – себестоимость продукции в текущем (отчетном) и базисном периодах;

Пример. Пусть предприятие во II квартале 2000 года изготовило 100 утюгов, которые реализовало по цене 60 грн. за 1 шт. При этом себестоимость изготовления утюгов равнялась 40 грн. за 1 шт. Во II квартале 2001 года это предприятие изготовило только 90 утюгов и реализовало их по цене 70 грн. за 1 шт. При этом себестоимость производства утюгов достигла 45 грн. за 1 шт.

Вычислим индивидуальные индексы объема, цены и себестоимости производства утюгов.

;;

На данном предприятии во II квартале 2001 г. по сравнению с тем же периодом 2000 г:

объем производства снизился на;

но при этом возросла цена продукции на ;

а себестоимость – возросла на .

Индивидуальные индексы для статистических исследований вычисляются крайне редко, так однородных совокупностей практически не бывает.

Основной формой общих индексов являются агрегатные индексы («aggrega» (лат.) – присоединять). В числители и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых сложных статистических совокупностей.

Для достижения сопоставимости разнородных единиц в сложных статистических совокупностях в индексные соотношения вводят специальные сомножители – так называемые, соизмерители. Они необходимы для перехода от натуральных измерений разнородных единиц к однородным показателям. При этом в числителе и знаменателе общего индекса изменяются лишь значения индексируемой величины, а их соизмерители остаются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода). Это необходимо для того, чтобы на величине индекса называлось лишь влияние фактора, который определяет изменения индексируемой величины.

(13.4)

Цена является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления цены () (отношение цены в отчетном периоде к базисному ).

Общий индекс физического объема.

(13.5)

Физический объем является количественным показателем, поэтому соизмерителем берем качественный показатель цены () и его период берем по знаменателю обозначения периода вычисления физического объема () (отношение физического объема в отчетном периоде к базисному )

Общий индекс себестоимости..

(13.6)

Себестоимость является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема () и обозначение его периода берем по числителю обозначения периода вычисления себестоимости () (отношение себестоимости в отчетном периоде к базисному )

Общий индекс товарооборота.

(13.7)

Общий индекс затрат на производство.

(13.8)

Рассмотрим индексный метод изучения динамики сложных статистических совокупностей на примерах.

Пример. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в табл. 13.1.

Как видно из табл. 13.1, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен.

,

II период (отчетный)

Цена за единицу товара, грн., ()

Количество товара, ()

Цена за единицу товара, грн., ()

Количество товара, ()

Физического объема,

Источник

Индексы в статистике

10.1. Понятие и виды статистических индексов

Общее определение индексов как статистических показателей можно сформулировать следующим образом.

Кроме характеристики интенсивности изменения самого явления, индексы могут выполнять и аналитическую функцию: на их основе определяют влияние различных факторов на развитие явления. Например, при формировании товарооборота можно проследить прирост его объема за счет индивидуальных изменений цен на товары и изменений в объеме продаж.

На основе индексов проводится оценка изменения средних показателей по однородной совокупности, например средней цены товара, продаваемого в разных регионах, в том числе за счет непосредственно роста уровня цен и за счет изменения структуры продаж.

Статистические индексы классифицируются по следующим направлениям (рис. 10.1):

Экономическое содержание выбранной базы сравнения позволяет провести деление всех индексов на динамические, территориальные и индексы сравнения с плановыми (нормативными) значениями показателей.

Последняя группа включает в себя индексы планового задания [показывают степень увеличения (снижения) показателя, предусмотренную планом], индексы выполнения плана (показывают соотношение между фактическим значением показателя и его плановым уровнем), индексы сравнения с нормативными значениями (например, индексы выполнения норм расходов материала).

По степени агрегирования, или охвата явления, индексы делятся на индивидуальные и сводные. Индивидуальный индекс характеризует изменение показателя у отдельной единицы совокупности (например, изменение цены на принтеры определенной марки). Сводный индекс выступает в качестве обобщенной характеристики изменения показателя в целом по всей совокупности разнородных единиц (изменение цен в целом на принтеры всех видов).

10.2. Индивидуальные индексы: правила их построения и анализа

Индивидуальный индекс представляет собой относительный показатель, характеризующий изменение отдельного элемента сложного экономического явления.

Методика исчисления индивидуальных индексов динамики социально-экономических показателей подобна методике расчета относительных величин: сравнивается абсолютное значение показателя в текущем и базисном периоде.

Величина, изменение которой изучается с помощью индекса, называется индексируемой величиной.

В индексной методологии принята следующая система обозначений:

Приведем примеры построения индивидуальных индексов:

Он показывает, как цена на данный товар в текущем периоде изменилась по сравнению с ценой этого же товара в базисном периоде;

Он позволяет сравнить физические объемы товарооборота (или производства продукции).

Аналогичным образом строятся индивидуальные индексы сравнения с плановыми или нормативными значениями, например индекс выполнения плана по объему продукции

В числителе и знаменателе территориальных индексов находятся значения показателя, относящиеся к двум сравниваемым территориям, например индивидуальный территориальный индекс цен на определенный товар будет иметь вид

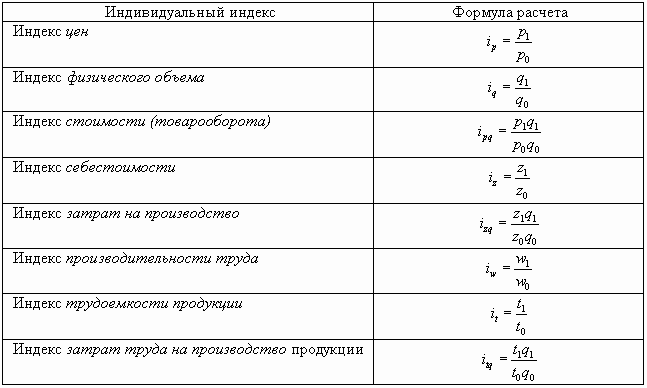
Ниже представлены формулы расчета индивидуальных индексов наиболее часто используемых экономических показателей.

Таблица 10.1.

Источник

14. Индексы в статистике: методы исчисления, примеры

«Индекс» в переводе с латинского – указатель, показатель.

В статистике под индексом понимается относительная величина, характеризующая соотношение значений определенного показателя во времени, пространстве, а также сравнение фактических данных с планом или другим нормативом.

С помощью индексов можно определить количественные изменения самых различных показателей функционирования народного хозяйства, развития социально-экономических процессов и т.п.

В экономической работе с помощью индексов можно объективно и точно показать изменения в росте или снижении производства, изменения в урожайности, состоянии себестоимости и цен выпускаемой продукции, численности работающих, производительности труда, заработной платы, изменения в цене акций на фондовых рынках (индекс Доу Джонса), сравнительную характеристику изменения погоды за определенный период времени (температуры, влажности, давления) и т.д. и т.п.

Индексы в своей основе представляют разновидность относительных величин, характеризующих средние показатели исследуемых процессов или явлений в социально-экономических и других областях деятельности общества. Однако от средних величин, рассмотрению которых посвящены были предыдущие темы, индексы отличаются тем, что они воплощают в себе, как правило, сводные, обобщающие показатели, т.е. выражают собой некоторое содержание, свойственное всем рассматриваемым явлениям и процессам.

Индексный метод имеет свою терминологию и символы.

Обозначения индексируемых величин:

i – индивидуальный индекс, его вычисляют для одной единицы совокупности;

I – общий (сводный) индекс (он определяется для всех единиц совокупности);

q – количество (объем) какого-либо товара в натуральном выражении;

p – цена единицы товара;

z – себестоимость единицы продукции;

t – затраты времени на производство единицы продукции, трудоемкость;

T – общие затраты времени на производство (tq) или численность рабочих;

pq – стоимость продукции или товарооборот;

zq – издержки производства.

Знак внизу справа означает период, например:

Экономический индекс – это относительная величина, которая характеризует изменение исследуемого явления во времени, в пространстве или по сравнению с некоторым эталоном (планируемым, нормативным уровнем и т.п.).

Если в качестве базы сравнения используется уровень за какой-либо предшествующий период – получают динамический индекс; если же базой является уровень того же явления по другой территории – территориальный индекс.

Индексируемая величина – показатель, изменение которого характеризуется индексом, она содержится в названии самого индекса, например: индекс цен, индекс заработной платы, индекс физического объема продукции и т.д.

Вес индекса – величина, служащая для целей соизмерения индексируемых величин.

Классификация индексов:

В экономическом анализе индексы используются не только для сопоставления уровней изучаемого явления, но главным образом для определения экономической значимости причин, объясняющих абсолютное различие сравниваемых уровней.

Экономические индексы позволяют: 1) измерить динамику социально-экономического явления за два и более периодов времени; 2) измерить динамику среднего экономического показателя; 3) измерить соотношение показателей по разным регионам; 4) определить степень влияния изменений значений одних показателей на динамику других; 5) пересчитать значения макроэкономических показателей из фактических цен в сопоставимые.

Методика построения агрегатного индекса предусматривает решение трех вопросов: 1) какая величина будет индексируемой; 2) по какому составу разнородных элементов явления необходимо исчислить индекс; 3) что будет служить весом при расчете индекса.

Правило при выборе индекса

При выборе веса индекса принято руководствоваться следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период, при построении индекса качественного показателя используются веса отчетного периода.

Расчет индивидуальных индексов

Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс, который характеризует изменение во времени экономических величин, относящихся к одному объекту, например:

– индекс цены определенного продукта (товара), где и цена товара, соответственно в текущем и в базисном периоде

‑ индекс объема одного определенного продукта (товара)

‑ индекс себестоимости единицы отдельного продукта

‑ индекс численности работников и т.д.

Все индивидуальные индексы показывают, каково соотношение между отчетным (со знаком «1») и базисным (со знаком «0») показателями или во сколько раз увеличилась (уменьшилась) индексируемая величина.

Все индивидуальные индексы по сути являются относительными величинами динамики или коэффициентами (темпами) роста (снижения).

Индивидуальные индексы характеризуют изменение отдельных единиц статистической совокупности. Характерной чертой индексов является то, что все они образуют системы взаимосвязанных показателей.

Расчеты индивидуальных индексов просты по своей сущности и выполняются путем вычисления отношения двух индексируемых величин. Индивидуальные индексы могут исчисляться в виде индексного ряда за несколько периодов.

Существуют два способа расчета индивидуальных индексов: цепной и базисный.

При цепном способе расчета за базу отношения принимается индексируемая величина соседнего прошлого периода, в этом случае база расчета в ряду постоянно меняется.

При базисном способе расчета за базу принимается индексируемая величина какого-либо отдельного периода.

Расчет общих индексов

В области экономических явлений наряду с индивидуальными индексами, характеризующими изменения единичных элементов, возникает необходимость расчета сводных относительных величин, обобщающих изменения определенного показателя в сложной совокупности, отдельные элементы которой несопоставимы (в физических единицах) и не могут суммироваться.

Например, нельзя тонны нефти и тонны стали, а также цены на разные товары (мясо, молоко, обувь, одежду и т.п.).

Для обобщения относительного изменения определенного показателя в сложной совокупности рассчитываются общие (сводные ) индексы.

Общий (сводный) индекс – показатель, измеряющий динамику сложного явления, составные части которого непосредственно несоизмеримы в физических единицах.

Например, по данным органов статистики, цены на продовольственные товары в декабре 2018 г. составили 116,1% по отношению к предыдущему месяцу (ноябрю) и 175 % по отношению к декабрю 2017 г.

С помощью общих индексов характеризуется изменение цен на товары, изменение уровня жизни, развитие производства отдельных отраслей и экономики в целом и многое другое.

Индексы могут иметь разный характер.

Одни являются объемными (количественными); другие условно можно назвать качественными: они представляют собой показатели, определяемые на какую-то единицу (цена единицы товара, себестоимость единицы продукции, урожайность с 1 га и т.д.).

В соответствии с этим и индексы можно подразделить на индексы количественных показателей (индекс физического объема производства, индекс продаж акций и т.п.) и качественных (индекс цен, индекс себестоимости, индекс заработной платы и пр.)

Каждый из этих индексов имеет свои особенности, но любой общий индекс может быть исчислен двумя способами: как агрегатный и как средний из индивидуальных.

Рассмотрим оба способа построения (исчисления) общих индексов.

Общий индекс, полученный путем сопоставления итоговых показателей, количественно выражающих сложное явление в отчетном и базисном периодах с помощью соизмерителей, называют агрегатным.

Соизмерители необходимы для перехода от натуральных измерителей, разнородных единиц статистической совокупности к однородным показателям.

При этом в числителе и знаменателе общего индекса изменяется только значение индексируемой величины, а их соизмерители являются постоянными величинами и фиксируются на одном уровне ‑ это необходимо для того, чтобы на величине индекса сказывалось лишь влияние фактора, который определяет изменения индексируемой величины.

Пример. В качестве соизмерителей индексируемых величин выступают тесно связанные с ними экономические показатели: цена, количество, себестоимость единицы продукции или затраты на единицу продукции и др.

При сравнении числителя и знаменателя данной формулы в разности определяется показатель абсолютного прироста.

При сравнении разности числителя и знаменателя индексного отношения получаем показатель, характеризующий прирост суммы в текущем периоде по сравнению с базисным периодом.

Обозначая объем продукции (товаров через q, а цены – через p, можно представить стоимость продукции в базисном периоде как , а в отчетном как . Сопоставляя эти два показателя, получим индекс стоимости (товарооборота).

Который показывает относительное изменение стоимости продукции как за счет изменения цен, так и за счет изменения объема отдельных товаров.

Если же продукцию двух сравниваемых периодов оценить в одних и тех же неизменных ценах, то очевидно, что стоимость продукции двух периодов будет отличаться лишь за счет изменения объема продукции. Поэтому общий индекс, исчисленный как отношение стоимости продукции двух периодов в одних и тех же ценах, называют агрегатный индекс физического объема .

В агрегатном индексе физического объема в качестве соизмерителя различных товаров принимаются цены базисного периода или цены, неизменные в течении ряда лет (такие цены называют также сопоставимыми).

где и ‑ объем продукции различных видов соответственно в базисном и отчетном периодах.

Отметим, что суммы в числителе и знаменателе имеют вполне реальный смысл:

‑ стоимость продукции базисного периода;

‑ стоимость продукции отчетного периода в базисных ценах.

Разность между числителем и знаменателем агрегатного индекса характеризует изменение в абсолютном выражении результативного показателя за счет изменения индексируемой величины.

Пример. Предположим, предприятие выпускает три вида неоднородной продукции. Данные о производстве и цены за два периода приведем в (табл. 14.1).

Таблица 14.1. – Данные о производстве продукции за 2 периода

Товар	Выработано тыс. единиц		Цена за единицу товара, руб.		Стоимость продукции в базисных ценах, тыс. руб.
	Базисный период q0	Отчетный период q1	Базисный период р0	Отчетный период р1	Базисный период q0p0	Отчетный период q1p0
А	80	60	13	16	1040	780
Б	50	30	18	20	900	540
В	40	35	6	8	240	210
ИТОГО	–	–	–	–	2180	1530

Следовательно, общий объем (выпуск) продукции в отчетном периоде по сравнению с базисным составил 70,2% (или снизился на 29,8%).

А в абсолютном выражении за счет уменьшения выпуска стоимость продукции в отчетном периоде снизилась на 650 тыс. руб., вычитаем из числителя знаменатель

Как уже отмечалось, при построении агрегатного индекса фи­зического объема могут использоваться и другие соизмерители. Так, например, если принять в качестве соизмерителей себестои­мость единицы продукции в базисном периоде z₀, то агрегатный индекс физического объема можно записать как:

Разность между числителем и знаменателем покажет, как изменились общие затраты (издержки) на производство в связи с изменением выпуска продукции:ли в качестве соизмерителей принять затраты времени на единицу продукции в базисном периоде, то формула агрегатного индекса физического объема будет иметь вид:

разность будет характеризовать изменение общих затрат времени на производство продукции за счет изменения объема выпуска.

Агрегатный индекс цен. По аналогии с индексом физического объема для определенного набора товаров (продуктов) может быть построен и агрегатный индекс цен (индекс качественного показателя). При этом рассуждения остаются теми же: если нельзя суммировать цены на различные товары, то можно суммировать и сопоставлять стоимости этих товаров.

Однако, сопоставляя два значения стоимости рq, мы должны показать изменение последней лишь за счет изменения цен р, т.е. необходимо устранить влияние изменения количества производи­мой (или реализуемой) в разные периоды продукции q на стоимостный показатель продукции. Для этого один и тот же количест­венный набор продуктов надо оценить в ценах отчетного и базисного периодов и затем сопоставить первую величину со вто­рой. Таким образом, в агрегатном индексе цен индексируемой величиной является, естественно, цена р, а соизмерителем (весами) ‑ количество произведенных (реализованных) товаров q, принятое на уровне базисного или отчётного периода.

Агрегатная формула общего индекса цен была впервые предложена в 1864 г. немецким ученым Э. Ласпейресом. Он предлагал строить агрегатный индекс цен, приняв в качестве весов продукцию базисного периода q₀:

В 1874 г. другой немецкий учёный, Г. Пааше, предложил строить агрегатный индекс цен по продукции текущего периода q₁:

Каждый из этих индексов имеет свои особенности, которым отдается предпочтение в конкретных условиях, использования.

Так, например, индекс Цен Ласпейреса удобен для оперативной (недельной, месячной, квартальной) информации об изменении цен на определенный фиксированный набор товаров, когда пересчет каждый раз на текущий набор (количество) товаров сопряжен с большими затратами, труда и времени.

По формуле Ласпейреса рассчитывают индекс потребительских цен (ИПЦ).

В то же время формуле Пааше отдается предпочтение, когда индекс цен рассматривается в системе с индексом стоимости и индексом физического объема. В этом случае, чтобы обеспечивать взаимосвязь между индексом стоимости и индексом физического объема.

Кроме того, при расчете индекса цен; по формуле Пааше, вычитая из числителя знаменатель, легко определить в абсолютном выражении сумму потерь (или прибыли) за счет изменения цен на продукцию отчетного (текущего) периода.

Рассмотрим расчет агрегатных индексов цен на примере.

Таблица 14.2. – Данные о реализации продукции за 2 периода (цифры условные)

измБазисный периодОтчетный периодСтоимость базисного периода, рубСтоимость отчетного периода, рубПро-дано ед. q₀Цена руб p₀Про-дано ед. q₁Цена руб p₁q₀p₀q₀p₁q₁p₀q₁p₁ГовядинаКг1000259003025000300002250027000КартофельКг3000240002,560007500800010000Молокол5000360003,215000160001800019200Всего46000535004850056200

Чтобы определить, как в среднем изменились цены на все продукты (или какова средняя величина изменения цен), рассчитаем сводный (общий) индекс цен в форме агрегат­ного индекса:

Расхождение не очень большое (на 0,4), но все же есть. Какому же индексу отдать предпочтение? На таком уровне исследования (по отдельному хозяйству и сово­купности хозяйств) предпочтение следует отдать индексу Пааше, поскольку он показывает реальное изменение стоимости продукции, реализованной в отчетном периоде, за счет изменения цен. В этом индексе числитель ‑ реальная величина, фактическая выручка, полученная от реализации продукции в отчетном периоде, а знаменатель ‑ условная величина, показываю­щая, какой была бы выручка, если бы продукция отчетною периода продавалась по базисным ценам.

Разность между ними, (56200 ‑ 48500 = 7700 руб.), показывает в данном случае, какую прибыль дополнительно получило хозяйство при ре­ализации продукции в отчетном периоде за счет роста цен.

В формуле же индекса цен Ласпейреса в знаменателе содержится реальная выручка (стоимость) от реализации в базисном периоде, а в числителе ‑ условная величина, характеризу­ющая, какой была бы выручка от реализации продукции базисного периода по ценам отчетного периода. Разность практически не представляет интереса, так как эта величина слишком отвлеченная: она показывает, насколько изменилась бы выручка (стоимость) в прошлом (базисном) периоде, если бы базисная про­дукция была реализована по текущим (отчетным) ценам.

Кроме того, при расчете индекса цен по формуле Пааше, легко увязываются изменения трех взаимосвязан­ных показателей: стоимости (выручки), объема реализации и цен. Так, по данным табл. 14.2 индекс стоимости продукции

(или 122,2%), т.е. стоимость продукции (выручка от продажи) в отчетном периоде увеличилась на 22,2%, что составило в абсолютном выражении 10200 руб. (56200 – 46000).

Индекс физического объема реализаций по данным табл. 14.2

В абсолютном выражении увеличение стоимости за счет изменения объема реализации составило 2500 руб. (48500 – 46000)

Таким образом, имеет место увязка индексов (относительного изменения показателей):

А также абсолютных изменений: в нашем примере 10200 = 7700 + 2500,т.е. общее изменение стоимости продукции равно сумме приростов за счет изменения цен и за счет изменения объема.

В начале XX в. американский экономист И. Фишер предложил вместо формул индексов цен Ласпейреса и Пааше использовать среднюю геометрическую из них, т.е. корень квадратный из произ­ведения индексов иен Ласпейреса и Пааше:

(Этот индекс назван им идеальным, поскольку в нем не отдается предпочтение ни продукция базисного периода, ни продукции текущего периода.

Кроме того, этот индекс «обратим» во времени, т.е. если рас­считывать индекс базисного периода к отчетному, он будет равен обратной величине первоначального индекса (т.е. отчетного периода к базисному). Другими словами, перемножение таких, «обратных» индексов дает единицу.

Однако индекс Фишера из-за его формальности и трудности экономической интерпретации используется редко, в основном при территориальных сопоставлениях.

Мы рассмотрели расчет агрегатных индексов физического объ­ема и цен как наиболее типичных представителей агрегатных индексов соответственно для количественных и качественных индек­сируемых показателей.

По аналогии можно записать агрегатные индексы для многих других показателей.

Контрольные задания

Источник