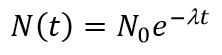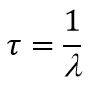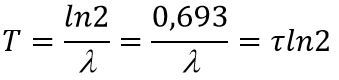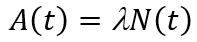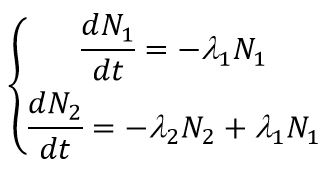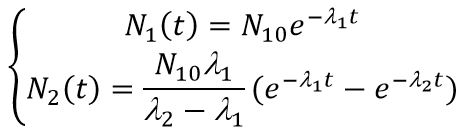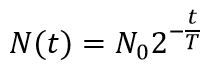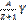Постоянная распада чему равна
Постоянная распада чему равна
При изучении процесса радиоактивного распада было установлено, что не все ядра радиоактивного изотопа распадаются одновременно, в каждую единицу времени распадается лишь некоторая доля общего числа радиоактивного элемента. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер.
N – число ядер, не распавшихся за время t,
λ – постоянная распада, различна для разных радиоактивных веществ.
Cреднее время жизни τ – промежуток времени τ, в течение которого система распадается с вероятностью 1 – 1/e:
Период полураспада – это время, в течение которого распадается половина радиоактивных ядер:
Активность радиоактивного препарата – число ядер этого препарата, распадающихся за секунду.
Активность измеряется в кюри (Ки) и беккерелях (Бк)
1 Ки = 3,7·10 10 распадов/c, 1 Бк = 1 распад/c, внесистемная единица активности – резерфорд (Рд). 1 Рд =10 6 Бк.
Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений:
Решением системы с начальными условиями N1(0) = N10; N2(0) = 0 будет
Для практического использования закон радиоактивного распада можно записать так :
Изотопы – разновидности одного и того же химического элемента, близкие по своим физико-химическим свойствам, но имеющие разную атомную массу. Название «изотопы» было предложено в 1912 английским радиохимиком Фредериком Содди, который образовал его из двух греческих слов: isos – одинаковый и topos – место. Изотопы занимают одно и то же место в клетке периодической системы элементов Менделеева.
Изотопами называются разновидности одного и того же химического элемента, атомы которых имеют одинаковый заряд ядра (и, следовательно, практически одинаковые электронные оболочки), но отличаются значениями массы ядра. По образному выражению Ф.Содди, атомы изотопов одинаковы «снаружи», но различны «внутри».
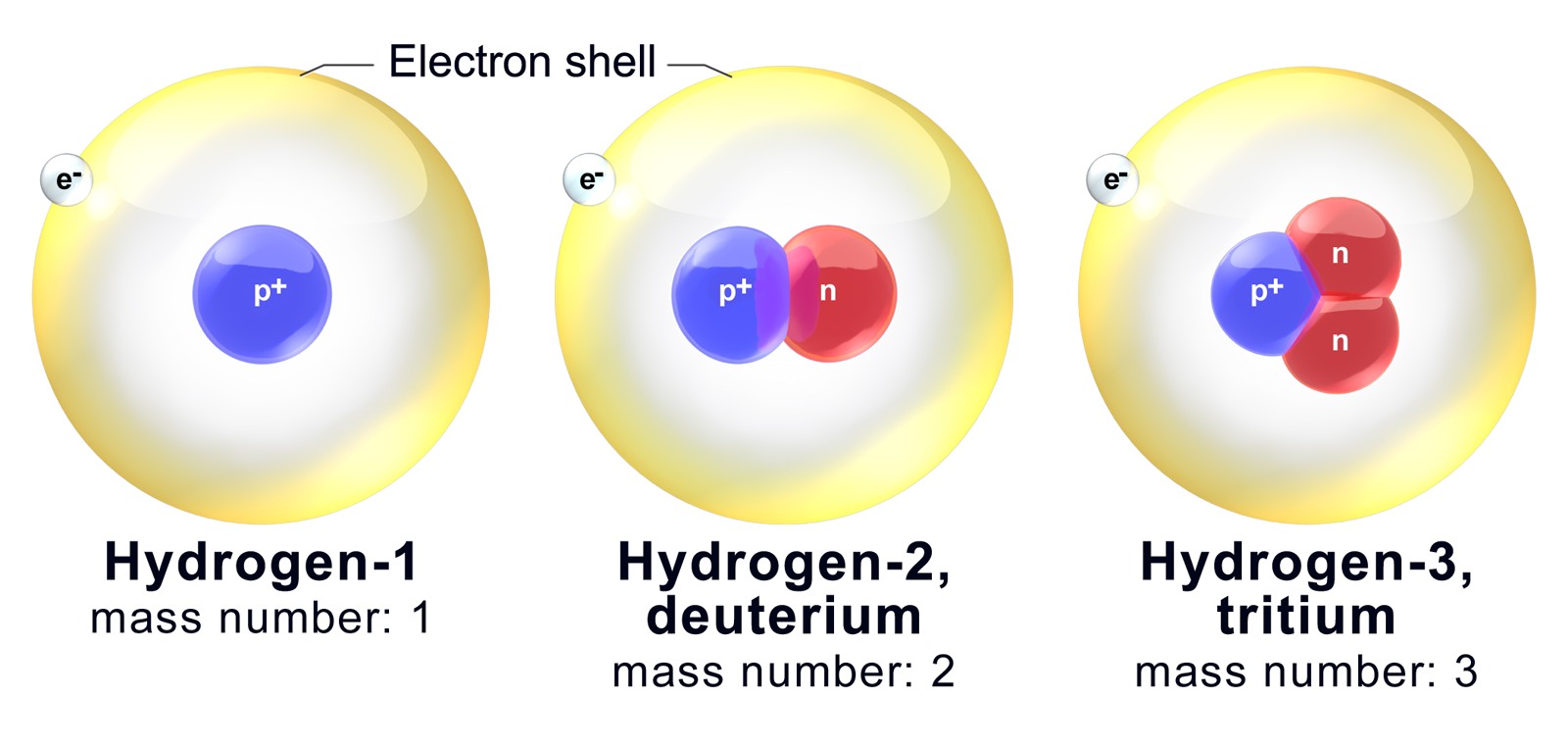
Из всех известных нам изотопов только изотопы водорода имеют собственные названия. Так, изотопы 2 H и 3 H носят названия дейтерия и трития и получили обозначения соответственно D и T (изотоп 1 H называют иногда протием).
В природе встречаются как стабильные изотопы, так и нестабильные – радиоактивные, ядра атомов которых подвержены самопроизвольному превращению в другие ядра с испусканием различных частиц (или процессам так называемого радиоактивного распада). Сейчас известно около 270 стабильных изотопов, причем стабильные изотопы встречаются только у элементов с атомным номером Z 83. Число нестабильных изотопов превышает 2000, подавляющее большинство их получено искусственным путем в результате осуществления различных ядерных реакций. Число радиоактивных изотопов у многих элементов очень велико и может превышать два десятка. Число стабильных изотопов существенно меньше, Некоторые химические элементы состоят лишь из одного стабильного изотопа (бериллий, фтор, натрий, алюминий, фосфор, марганец, золото и ряд других элементов). Наибольшее число стабильных изотопов – 10 обнаружено у олова, у железа, например, их – 4, у ртути – 7.
Для изучения свойств изотопов и особенно для их применения в научных и прикладных целях требуется их получение в более или менее заметных количествах. В первую очередь были освоены физико-химические методы разделения, основанные на различиях в таких свойствах изотопов одного итого же элемента, как скорости испарения, константы равновесия, скорости химических реакций и т.п. Наиболее эффективными среди них оказались методы ректификации и изотопного обмена, которые нашли широкое применение в промышленном производстве изотопов легких элементов: водорода, лития, бора, углерода, кислорода и азота.
Постоянная распада. Период полураспада. Активность. Виды радиоактивного распада и их спектры



Радиоактивность. Основной закон радиоактивного распада.
Эрнест Резерфорд – строение атома 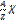
Виды радиоактивного распада:
α-распад: 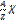
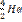
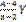
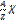
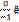
Число нераспавшихся радиоактивных ядер убывает по экспонициальному закону. Л(лямбда)-постоянная распада.
Постоянная распада. Период полураспада. Активность. Виды радиоактивного распада и их спектры.
Л(лямбда)-постоянная распада, пропорциональная вероятности распада радиоактивного ядра и различная для разных радиоактивных веществ.
Период полураспада (T)- это время, в течение которого распадается половина радиоактивных ядер. T=ln2/л=0,69/л.
[A]-беккерель (Бк)= 1распад/секунду.
[А]-резерфорд(Рд). 1Рд=10 6
Виды радиоактивного распада. Правило смещения.
Альфа-распад(самое слабое): А Z X> 4 2 He + A-4 Z-2Y
Характеристики взаимодействия заряженных частиц с веществом: линейная плотность ионизации, линейная тормозная способность, средний линейный пробег. Проникающая и ионизирующая способности альфа, бета и гамма излучения.
Заряженные частицы, распространяясь в веществе, взаимодействуют с электронами и ядрами, в результате чего изменяется состояние как вещества, так и частиц.
Линейная тормозная способность-это отношение энергии dE, теряемой заряженной ионизирующей частицей при прохождении элементарного пути dL, к длине этого пути. S= dE/dL.
Средний линейный пробег- это расстояние, которое ионизирующая частица проходит в веществе без столкновения. R-средний линейный пробег.
Проникающая способность всех видов ионизирующего излучения зависит от энергии.
Лекция 2. Основной закон радиоактивного распада и активность радионуклидов
Лекция 2. Основной закон радиоактивного распада и активность радионуклидов
Скорость распада радионуклидов различна – одни распадаются быстрее, другие – медленнее. Показателем скорости радиоактивного распада является постоянная радиоактивного распада, λ [сек-1], которая характеризует вероятность распада одного атома за одну секунду. Для каждого радионуклида постоянная распада имеет своё значение, чем оно больше, тем быстрее распадаются ядра вещества.
Число распадов, регистрируемых в радиоактивном образце за единицу времени, называют активностью (a), или радиоактивностью образца. Значение активности прямо пропорционально количеству атомов N радиоактивного вещества:
где λ – постоянная радиоактивного распада, [сек-1].
В настоящее время, согласно действующей Международной системе единиц СИ, за единицу измерения радиоактивности принят беккерель [Бк]. Своё название эта единица получила в честь французского учёного Анри Беккереля, открывшего в 1856 г. явление естественной радиоактивности урана. Один беккерель равен одному распаду в секунду 1 Бк = 1 
Однако до сих пор достаточно часто применяется внесистемная единица активности – кюри [Ки], введённая супругами Кюри как мера скорости распада одного грамма радия (в котором происходит
3,7·1010 распадов в секунду), поэтому
Эта единица удобна для оценки активности больших количеств радионуклидов.
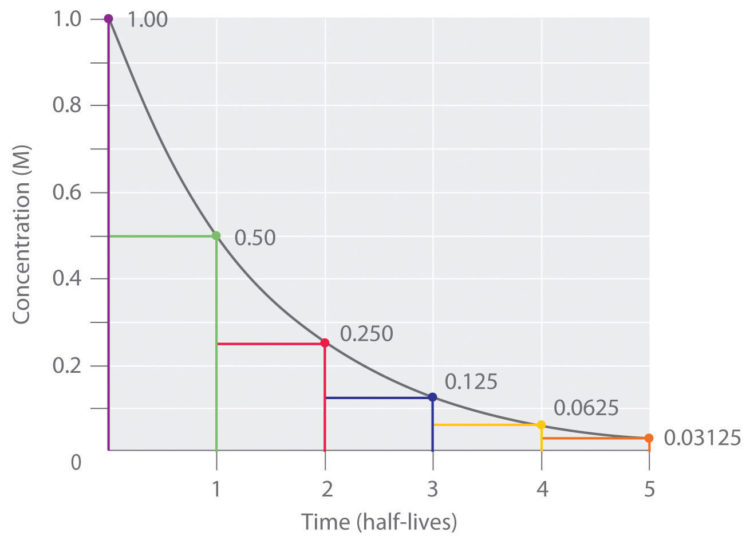
Снижение концентрации радионуклида во времени в результате распада подчиняется экспоненциальной зависимости:

где Nt – количество атомов радиоактивного элемента оставшихся через время t после начала наблюдения; N0 – количество атомов в начальный момент времени (t=0); λ – постоянная радиоактивного распада.
Описанная зависимость называется основным законом радиоактивного распада.
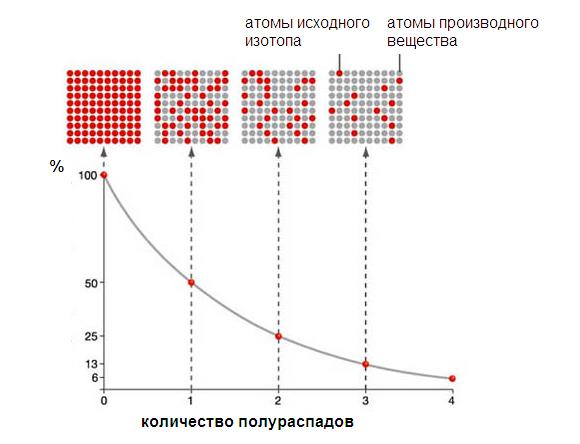
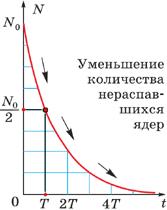
Время, за которое распадается половина от общего количества радионуклидов, называется периодом полураспада, Т½. Через один период полураспада из 100 атомов радионуклида остаются только 50 (рис. 2.1). За следующий такой же период из этих 50 атомов остаются лишь 25 и так далее.
Связь между периодом полураспада и постоянной распада выводится из уравнения основного закона радиоактивного распада:
при t=T½ и
получаем 




т. е. 

Поэтому закон радиоактивного распада можно записать следующим образом:

Активность at любого радиоактивного препарата по истечении времени t определяют по формуле, соответствующей основному закону радиоактивного распада:

где at – активность препарата через время t; a0 – активность препарата в начальный момент наблюдения.
Часто необходимо определить активность заданного количества любого радиоактивного вещества.
Вспомним, что единица количества вещества – моль. Моль – это количество вещества, содержащее столько же атомов, сколько их содержится в 0,012 кг=12 г изотопа углерода 12С.
В одном моле любого вещества содержится число Авогадро NA атомов:
Для простых веществ (элементов) масса одного моля численно соответствует атомной массе А элемента
Например: Для магния: 1 моль 24Mg = 24 г.
Для 226Ra: 1 моль 226Ra = 226 г и т. д.
С учётом сказанного в m граммах вещества будет N атомов:

С учётом уравнений (3.2.1) и (3.2.5) активность a простого элемента будет:

Пример: Подсчитаем активность 1-го грамма 226Ra, у которого λ = 1.38·10-11 сек-1.
a = 1.38·10-11·1/226·6,02·1023 = 3,66·1010 Бк.
Если радиоактивный элемент входит в состав химического соединения, то при определении активности препарата необходимо учитывать его формулу. С учётом состава вещества определяется массовая доля χ радионуклида в веществе, которая определяется соотношением:

где mрн – атомная масса радионуклида в соединении, Aв – атомная масса вещества.
С учётом уравнений (3.2.6) и (3.2.7) активность aв соединения будет определяться формулой:
Пример решения задачи
Активность А0 радиоактивного элемента 32Р в день наблюдения составляет 1000 Бк. Определить активность и количество атомов этого элемента через неделю. Период полураспада Т½ 32Р = 14,3 дня.
а) Найдём активность фосфора-32 через 7 суток:

б) Рассчитаем количество атомов в образце:

1) Что такое активность радионуклида?
2) Назовите единицы радиоактивности и связь между ними.
3) Что такое постоянная радиоактивного распада?
4) Дайте определение основному закону радиоактивного распада.
5) Что такое период полураспада?
6) Какая существует связь между активностью и массой радионуклида? Напишите формулу.
1. Рассчитайте активность 1 г 226Ra. Т½ = 1602 года.
2. Рассчитайте активность 1 г 60Со. Т½ = 5,3 года.
4. Рассчитайте активность 137Cs через 10 лет, если в начальный момент наблюдения она равна 1000 Бк. Т½ = 30 лет.
5. Рассчитайте активность 90Sr год назад, если в настоящий момент времени она равна 500 Бк. Т½ = 29 лет.
6. Какую активность будет создавать 1 кг радиоизотопа 131I, Т½ = 8,1 дня?
7. Пользуясь справочными данными, определите активность 1 г 238U. Т½ = 2,5·109 лет.
Пользуясь справочными данными, определите активность 1 г 232Th, Т½ = 1,4·1010 лет.
8. Рассчитайте активность соединения: 239Pu316O8.
9. Вычислите массу радионуклида активностью в 1 Ки:
9.3. 137Cs, Т1/2=30 лет;
9.4. 239Pu, Т1/2=2,4·104 лет.
10. Определите массу 1 мКи радиоактивного изотопа углерода 14С, Т½ = 5560 лет.
11. Необходимо приготовить радиоактивный препарат фосфора 32P. Через какой промежуток времени останется 3 % препарата? Т½ = 14,29 сут.
12. В природной смеси калия содержится 0,012 % радиоактивного изотопа 40К.
1) Определите массу природного калия, в котором содержится 1 Ки 40К. Т½ = 1,39·109 лет = 4,4·1018 сек.
2) Рассчитайте радиоактивность грунта по 40К, если известно, что содержание калия в образце грунта – 14 кг/т.
13. Сколько периодов полураспада требуется для того, чтобы первоначальная активность радиоизотопа снизилась до 0,001 %?
14. Для определения влияния 238U на растения семена замачивали в 100 мл раствора UO2(NO3)2·6H2O, в котором масса радиоактивной соли составляла 6 г. Определите активность и удельную активность 238U в растворе. Т½ = 4,5·109 лет.
15. Определите активность 1 грамма 232Th, Т½ = 1,4·1010 лет.
16. Определите массу 1 Ки 137Cs, Т1/2=30 лет.
17. Соотношение между содержанием стабильных и радиоактивного изотопов калия в природе – величина постоянная. Содержание 40К равно 0,01%. Рассчитайте радиоактивность грунта по 40К, если известно, что содержание калия в образце грунта – 14 кг/т.
18. Литогенная радиоактивность окружающей среды формируется преимущественно за счёт трёх основных природных радионуклидов: 40К, 238U, 232Th. Доля радиоактивных изотопов в природной сумме изотопов составляет 0,01, 99,3,
100 соответственно. Рассчитайте радиоактивность 1 т грунта, если известно, что относительное содержание калия в образце грунта 13600 г/т, урана – 1·10-4 г/т, тория – 6·10-4 г/т.
19. В раковинах двустворчатых моллюсков обнаружено 23200 Бк/кг 90Sr. Определите активность образцов через 10, 30, 50, 100 лет.
21. 241Am (Т½ = 4,32·102 лет) образуется из 241Pu (Т½ = 14,4 лет) и является активным геохимическим мигрантом. Пользуясь справочными материалами, рассчитайте с точностью до 1% уменьшение активности плутония-241 во времени, в каком году после Чернобыльской катастрофы образование 241Am в окружающей среде будет максимальным.
22. Рассчитайте активность 241Am в продуктах выбросах Чернобыльского реактора по состоянию на апрель
2015 г., при условии, что в апреле 1986 г. активность 241Am составила 3,82·1012 Бк, Т½ = 4,32·102 лет.
23. В образцах грунта обнаружено 390 нКи/кг 137Cs. Рассчитайте активность образцов через 10, 30, 50, 100 лет.
24. Средняя концентрация загрязнения ложа оз. Глубокого, расположенного в Чернобыльской зоне отчуждения, составляет 6,3·104 Бк 241Am и 7,4·104 238+239+240Pu на 1 м2. Рассчитайте, в каком году получены эти данные.
Постоянная распада чему равна
Проинтегрировав (1) получим закон радиоактивного распада
Активность измеряется в кюри (Ки) и беккерелях (Бк)
1 Ки = 3.7·10 10 распадов/c,
1 Бк = 1 распад/c.
Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений
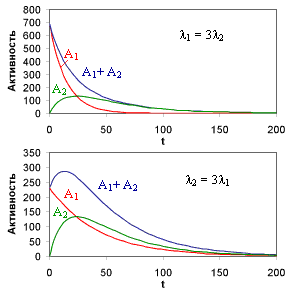
Количество ядер 2 достигает максимального значения 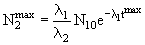
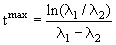
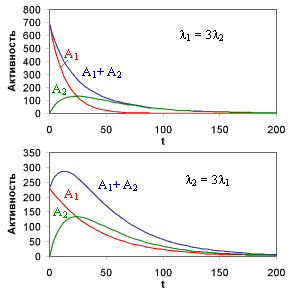
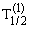
Если λ2 >λ1 ( 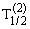
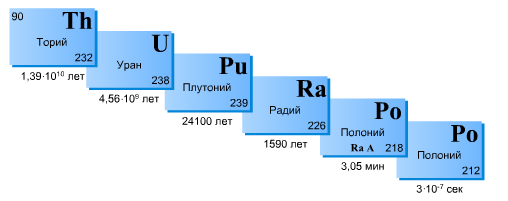
Поэтому в естественном состоянии все изотопы, генетически связанные в радиоактивных рядах, обычно находятся в определенных количественных соотношениях, зависящих от их периодов полураспада.
В общем случае, когда имеется цепочка распадов 1→2→. n, процесс описывается системой дифференциальных уравнений
Решением системы (10) для активностей с начальными условиями N1(0) = N10; Ni(0) = 0 будет
Штрих означает, что в произведении, которое находится в знаменателе, опускается множитель с i = m.
Закон радиоактивного распада
Появление «ручных» сцинтилляционных счетчиков и, главным образом, счётчиков Гейгера–Мюллера, которые помогли автоматизировать подсчёты частиц (см. § 15-е), привело физиков к важному выводу. Любой радиоактивный изотоп характеризуется самопроизвольным ослабеванием радиоактивности, выражающимся в уменьшении количества распадающихся ядер в единицу времени.
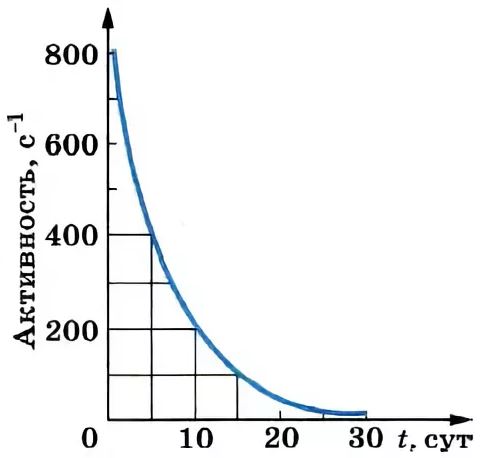
Построение графиков активности различных радиоактивных изотопов приводило учёных к одной и той же зависимости, выражающейся показательной функцией (см. график). По горизонтальной оси отложено время наблюдения, а по вертикальной – количество нераспавшихся ядер. Кривизна линий могла быть различной, однако сама функция, которой выражались описываемые графиками зависимости, оставалась одной и той же:
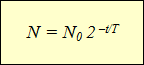 | N – количество нераспавшихся ядер N0 – начальное количество ядер t – время наблюдения, с T – период полураспада, с |
Эта формула выражает закон радиоактивного распада: количество нераспавшихся с течением времени ядер определяется как произведение начального количества ядер на 2 в степени, равной отношению времени наблюдения к периоду полураспада, взятой с отрицательным знаком.
Как выяснилось в ходе опытов, различные радиоактивные вещества можно охарактеризовать различным периодом полураспада – временем, за которое количество ещё нераспавшихся ядер уменьшается вдвое (см. таблицу).
| Йод-129 | 15 млн лет | Углерод-14 | 5,7 тыс лет |
| Йод-131 | 8 дней | Уран-235 | 0,7 млрд лет |
| Йод-135 | 7 часов | Уран-238 | 4,5 млрд лет |
Период полураспада – общепринятая физическая величина, характеризующая скорость радиоактивного распада. Многочисленные опыты показывают, что даже при очень длительном наблюдении за радиоактивным веществом его период полураспада постоянен, то есть не зависит от числа уже распавшихся атомов. Поэтому закон радиоактивного распада нашёл применение в методе определения возраста археологических и геологических находок.
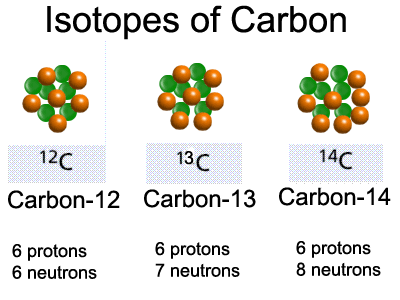
Метод радиоуглеродного анализа. Углерод – очень распространённый на Земле химический элемент, в состав которого входят стабильные изотопы углерод-12, углерод-13 и радиоактивный изотоп углерод-14, период полураспада которого составляет 5,7 тысяч лет (см. таблицу). Живые организмы, потребляя пищу, накапливают в своих тканях все три изотопа. После прекращения жизни организма поступление углерода прекращается, и с течением времени его содержание убывает естественным путём, за счёт радиоактивного распада. Поскольку распадается только углерод-14, с течением веков и тысячелетий изменяется соотношение изотопов углерода в ископаемых останках живых организмов. Измерив эту «углеродную пропорцию», можно судить о возрасте археологической находки.
Метод радиоуглеродного анализа применим и для геологических пород, а также для ископаемых предметов быта человека, но при условии, что соотношение изотопов в образце не было нарушено за время его существования, например, пожаром или действием сильного источника радиации. Неучёт подобных причин сразу после открытия этого метода приводил к ошибкам на несколько веков и тысячелетий. Сегодня применяются «вековые калибровочные шкалы» для изотопа углерода-14, исходя из его распределения в долгоживущих деревьях (например, в американской тысячелетней секвойе). Их возраст можно подсчитать весьма точно – по годовым кольцам древесины.
Предел применения метода радиоуглеродного анализа в начале XXI века составлял 60 000 лет. Для измерения возраста более древних образцов, например горных пород или метеоритов, используют аналогичный метод, но вместо углерода наблюдают за изотопами урана или других элементов в зависимости от происхождения исследуемого образца.