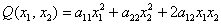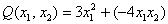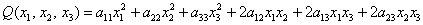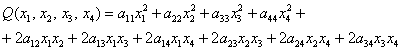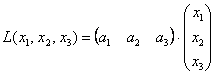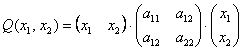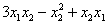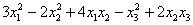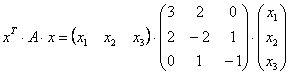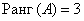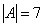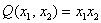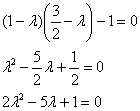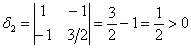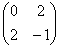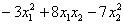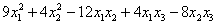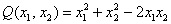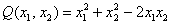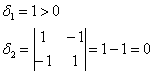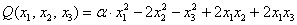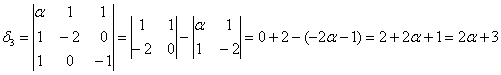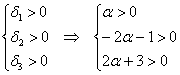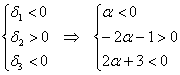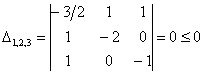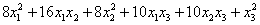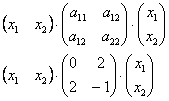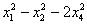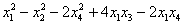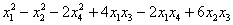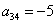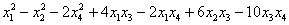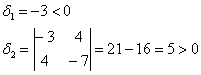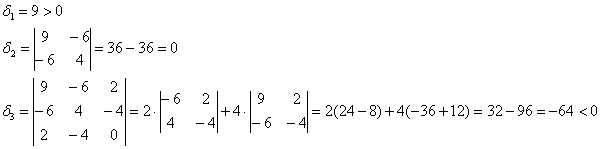положительный индекс квадратичной формы

Квадратичные формы 2

Квадратичные формы 2

Число положительных квадратов в той нормальной форме, к которой приводится данная действительная квадратичная форма f, называется положительным индексом инерции этой формы. Число отрицательных квадратов называется отрицательным индексом инерции. Разность между положительным и отрицательным индексами инерции называется сигнатурой формы f. При заданном ранге формы задание любого из этих трёх чисел определяет два других.

Теорема. Две квадратичные формы то п неизвестных с действительными коэффициентами тогда и только тогда переводятся друг в друга невырожденными действительными линейными преобразованиями, если эти формы имеют одинаковые ранги и одинаковые сигнатуры.

Пусть форма f переводится в форму g невырожденным действительным преобразованием. Это преобразование не меняет ранга формы. Оно не может менять и сигнатуры, так как в противном случае f и g приводились бы к различным нормальным видам, а тогда форма f приводилась бы к этим обоим нормальным видам, что противоречило бы закону инерции. Обратно, если формы f и g имеют одинаковые ранги и одинаковые сигнатуры, то они приводятся к одному и тому же нормальному виду и поэтому могут быть переведены друг в друга.

Пусть дана квадратичная форма g в каноническом виде

(1)

с не равными нулю действительными коэффициентами, то ранг этой формы равен, очевидно, r. Применяя известный способ приведения такой формы к нормальному виду, получим, что положительный индекс инерции формы равен числу положительных коэффициентов в правой части равенства (1). Тогда из предыдущей теоремы следует такой вывод:

Квадратичная форма f тогда и только тогда будет иметь форму (9) своим каноническим видом, если ранг формы f равен r, и положительный индекс инерции этой формы совпадает с числом положительных коэффициентов в (9).

Распадающиеся квадратичные формы

Если перемножить две линейные формы от п переменных

, ,

получится некоторая квадратичная форма. Не всякая квадратичная форма может быть представлена в виде произведения двух линейных форм. Определим условия, при которых это можно сделать, то есть квадратичная форма является распадающейся.

Комплексная квадратичная форма распадается тогда и только тогда, если её ранг меньше или равен двум. Действительная квадратичная форма распадается тогда и только тогда, если её ранг не больше единицы, или же он равен двум, а сигнатура равна нулю.

Если хотя бы одна из двух форм j и y нулевая, то их произведение – квадратичная форма с нулевыми коэффициентами и рангом 0. Если линейные формы j и y пропорциональны: j = сy, причём с ¹ 0 и форма j ненулевая, то пусть коэффициент а1 отличен от нуля. Тогда невырожденное линейное преобразование

при i = 2,3,…,n

приводит квадратичную форму jy к виду

Ясно, что квадратичная форма jy имеет ранг 1. Если линейные формы j и y не являются пропорциональными, то пусть, например,

.

Тогда линейное преобразование

,

,

при i = 3,4,…,п

невырожденное, и оно приводит квадратичную форму jy к виду jy = у1у2. В правой части стоит квадратичная форма ранга 2, имеющая в случае действительных коэффициентов сигнатуру 0.

Докажем обратное утверждение. Квадратичная форма ранга 0 может рассматриваться как произведение двух линейных форм, одна из которых нулевая. Квадратичная форма ранга 1 невырожденным линейным преобразованием приводится к виду

, с ¹ 0,

Выражая у1 линейно через х2,…, хп, получаем представление формы f в виде произведения двух линейных форм. Действительная квадратичная форма ранга 2 и сигнатуры 0 приводится невырожденным линейным преобразованием к виду

(2)

К этому же виду может быть приведена любая комплексная квадратичная форма ранга 2. Так как

,

то в правой части (2) после замены у1 и у2 их линейными выражениями через будет стоять произведение двух линейных форм.

Положительно определённые формы

Квадратичная форма f от п переменных с действительными коэффициентами называется положительно определённой, если она приводится к нормальному виду, состоящему из п положительных квадратов, то есть её ранг и положительный индекс инерции равны числу переменных.

Теорем а. Квадратичная форма f от п переменных с действительными коэффициентами тогда и только тогда будет положительно определённой, если при всех действительных значениях этих переменных, хотя бы одна из которых отлична от нуля, эта форма принимает положительные значения.

Доказательство. Пусть форма f положительно определённая, то есть приводится к нормальному виду

, j = 1,2,…,п (2)

имеет отличный от нуля определитель из действительных коэффициентов аij. Если подставить в f произвольные действительные значения переменных , хотя бы одно из которых отлично от нуля, то можно сделать так: сначала подставить их в (2), а затем значения, полученные для всех yi – в (1). Значения, полученные для y1, y2,…, yn не могут все равняться нулю, так как в этом случае получилось бы, что система линейных однородных уравнений

i = 1,2,…,n,

имеет ненулевое решение, хотя её определитель отличен от нуля. Подставляя найденные для y1, y2,…, yn значения в (1), получим значения формы f, равное сумме квадратов п действительных чисел, которые не все равны нулю, то есть значение строго положительное.

Пусть теперь форма f не является положительно определённой, то есть или её ранг или положительный индекс инерции меньше п. Это означает, что в нормальном виде этой формы, к которому она приводится невырожденным линейным преобразованием (2), квадрат хотя бы одной из новых переменных, например yn, или отсутствует совсем, или содержится со знаком минус. В этом случае можно подобрать такие действительные значения для переменных х1,х2,…,хn, не все равные нулю, что значение формы f при этих значениях переменных равно нулю или отрицательно. Такими будут, например, те значения х1,х2,…,хn, которые получаются при решении по правилу Крамера системы линейных уравнений, получающейся из (2) при y1 = y2 =… = yn–1 = 0, yп = 1. Действительно, при этих значениях переменных х1,х2,…,хn форма f равна нулю, если yп2 не входит в нормальный вид этой формы, и равна –1, если yп2 входит в нормальный вид со знаком минус.

С помощью доказанной теоремы нельзя по коэффициентам формы установить, будет ли эта форма положительно определённой.

Пусть дана квадратичная форма f от п переменных с матрицей А = (aij). Миноры порядка 1,2,…,п этой матрицы, расположенные в её левом верхнем углу, то есть миноры

a11, , ,

из которых последний совпадает с определителем матрицы А, называются главными минорами формы f.

Теорема. Квадратичная форма f от п переменных с действительными коэффициентами тогда и только тогда будет положительно определённой, если все её главные миноры положительны.

Доказательство. При п = 1 теорема верна так как форма имеет в этом случае вид ах2 и поэтому положительно определена тогда и только тогда, если а > 0. Будем доказывать теорему для случая п переменных, предполагая, что для квадратичных форм от п – 1 переменных она уже доказана.

1) Если квадратичная форма f с действительными коэффициентами, составляющими матрицу А, подвергается невырожденному линейному преобразованию с действительной матрицей Q, то знак определителя формы (то есть определителя её матрицы) не меняется.

Действительно, после преобразования получаем квадратичную форму с матрицей QТАQ, однако, ввиду detQТ = detQ

то есть определитель detА умножается на положительное число.

2) Пусть теперь дана квадратичная форма

Её можно записать в виде

, (3)

где j будет квадратичной формой ль п – 1 переменных, составленной из тех членов формы f, в которые не входит переменная хп. Главные миноры формы j совпадают со всеми, кроме последнего, главными минорами формы f.

Пусть форма f положительно определена. Форма j также будет в этом случае положительно определенной. Если бы существовали такие значения переменных х1,х2,…,хn–1, не все равные нулю, при которых форма j получает не строго положительное значение, то, полагая дополнительно хn = 0, получили бы, ввиду (3), также не строго положительное значение формы f, хотя не все значения переменных х1,х2,…,хn–1,хn равны нулю. Поэтому, по индуктивному предположению, все главные миноры формы j, то есть все главные миноры формы f, кроме последнего, строго положительны. Что касается последнего главного минора формы f, то есть определителя самой матрицы А, то его положительность вытекает из следующих соображений: форма f, ввиду её положительной определённости, невырожденным линейным преобразованием приводится к нормальному ввиду, состоящему из п положительных квадратов. Определитель этого нормального вида строго положителен, а поэтому ввиду сделанного выше замечания положителен и определитель самой формы f.

Пусть теперь положительны все главные миноры формы f. Из этого следует положительность всех главных миноров формы j, то есть по индуктивному предположению, положительная определённость этой формы. Существует, следовательно, такое невырожденное линейное преобразование переменных х1,х2,…,хn, которое приводит форму j к виду суммы п – 1 положительных квадратов от новых переменных y1, y2,…,yn – 1. Это линейное преобразование можно дополнить до невырожденного линейного преобразования всех переменных х1,х2,…,хn, полагая хn = yn. Ввиду (3) форма f приводится указанным преобразованием к виду

(4)

Точные выражения для коэффициентов bin здесь несущественны. Так как

,

то невырожденное линейное преобразование

i = 1,2,…,n – 1,

приводит, ввиду (4) форму f к каноническому виду

Для доказательства положительной определённости формы f остаётся доказать положительность числа с. Определитель формы, стоящей в правой части равенства (5), равен с. Этот определитель должен быть положительным, так как правая часть равенства (5) получена из формы f двумя невырожденными линейными преобразованиями, а определитель формы f был, как последний из главных миноров этой формы, положительным.

Замети, что по аналогии с положительно определёнными квадратичными формами можно ввести отрицательно определённые формы, то есть такие невырожденные квадратичные формы с действительными коэффициентами, нормальный вид которых содержит лишь отрицательные квадраты переменных.

Источник

Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра

Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась 🙂

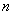
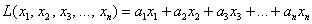
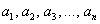
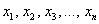
Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную. Линейной формой переменных называют однородный многочлен 1-й степени:

, где:

– какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля), а – переменные, которые могут принимать произвольные значения.

* В рамках данной темы будем рассматривать только действительные числа.

С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений, и в данном случае он подразумевает, что у многочлена нет приплюсованной константы .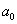

Например: 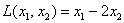– линейная форма двух переменных

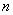
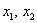
Теперь форма квадратичная. Квадратичной формой переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных имеет следующий вид:

Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
– в этом слагаемом находится произведение и (квадрат);
– здесь произведение ;
– и здесь произведение .

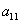
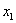
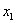
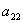
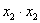
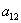
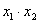
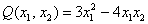
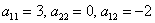
Далее будем полагать, что хотя бы одна из констант не равна нулю, и вот, пожалуйста, «неполный» пример: , в котором:

– сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому:

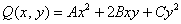
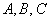
Иногда встречается «школьный» вариант оформления в духе , но то лишь иногда. Кстати, заметьте, что константы нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.

И квадратичная форма трёх переменных содержит уже шесть членов:

…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.

Далее ситуация начинает усугубляться:

и усугублять мы её дальше не будем, т.к. формы с бОльшим количеством переменных встречаются довольно редко.

Однако общую формулу запишем, её удобно оформить «простынёй»:

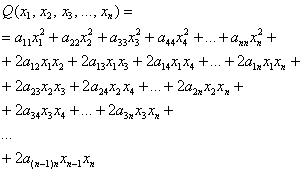
– внимательно изучаем каждую строчку – ничего страшного тут нет!

Квадратичная форма содержит 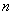слагаемых с квадратами переменных и слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний). Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).

Матричная запись квадратичной формы

Как на счёт матриц? 🙂 Знаю, знаю, соскучились. В практических задачах широко распространенная матричная запись квадратичных форм. Объяснения опять начну с формы линейной, например, от трёх переменных: 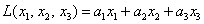. Её можно записать, как произведение двух матриц:

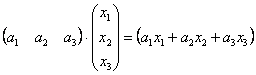
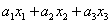
И действительно, выполняя матричное умножение, получаем матрицу «один на один»: , единственный элемент которой можно эквивалентно записать вне матрицы: .

Легко понять, что линейная форма «эн» переменных записывается в виде:

Квадратичная форма представима в виде произведения уже трёх матриц:

, где:

– столбец переменных;

– его транспонированная строка;

– матрица квадратичной формы.

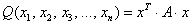
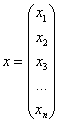
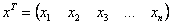
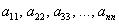
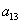
Это так называемая симметрическая матрица, на главной диагонали которой расположены коэффициенты при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например, – в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).

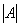
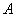
Определитель называют дискриминантом квадратичной формы, а ранг матрицы – рангом квадратичной формы.

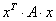
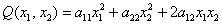
Если перемножить три матрицы , то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае . Согласно общей формуле, матричная запись данной формы имеет следующий вид:

И в самом деле: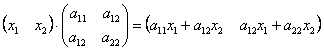

далее: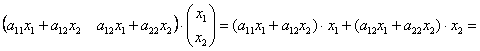

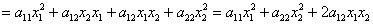
, в чём и требовалось убедиться.

Как вариант, сначала можно было перемножить правые матрицы, и затем первую матрицу умножить на полученный результат.

Вам понравилось так же, как и мне? Ну тогда пример для самостоятельного решения =)

Записать квадратичную форму в матричном виде и выполнить проверку. Определить дискриминант и ранг формы.

…что-то смущает? 😉 Краткое решение и ответ в конце урока! Статьи об определителе и ранге матрицы – в помощь.

После чего разберём аналогичную задачу с формой трёх переменных:

Записать матрицу квадратичной формы, найти её ранг и дискриминант

Решение: сбросим тяжёлую ношу лишних формул, и будем ориентироваться на сами члены:

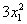
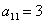
– слагаемое дважды содержит 1-ю переменную, поэтому ;

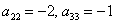
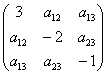
– из аналогичных соображений определяем и сразу записываем результаты на главную диагональ симметрической матрицы: .

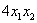
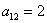
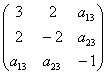
Так как в слагаемое входят 1-я и 2-я переменная, то (не забываем поделить на 2) и данный коэффициент занимает свои законные места: .

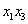
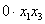
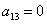
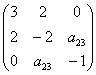
Поскольку в форме отсутствует член с произведением (а точнее, присутствует с нулевым множителем: ), то , и на холст отправляются два нуля: .

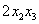
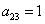
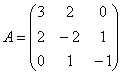
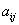
И, наконец, из слагаемого определяем , после чего картина завершена:
– матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений» , но и заставили их работать на себя!

По условию не требовалось записывать матричное уравнение, однако науки ради:

Желающие могут перемножить три матрицы, в результате чего должна получиться исходная квадратичная форма.

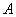
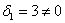
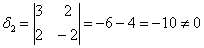
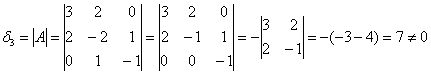
Теперь определим ранг формы. Он равен рангу матрицы . Так как в матрице есть хотя бы один ненулевой элемент, например, , то ранг не меньше единицы. Теперь вычислим минор , значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
, значит,

Если не очень понятно, что к чему, обязательно изучите статью о ранге матрицы – это довольно замысловатая задачка, и перед нами оказался лишь простой случай, когда угловые миноры не равны нулю.

Дискриминант квадратичной формы получен автоматом.

Ответ: , ранг равен трём, дискриминант

Следующее задание для самостоятельного решения:

Восстановить квадратичную форму по её матрице

При этом не нужно вспоминать никаких формул! Решение почти устное:

– сначала смотрим на главную диагональ и записываем слагаемые с квадратами переменных;

– затем анализируем симметричные элементы 1-й строки (или 1-го столбца), и записываем все слагаемые, в которые входит 1-я переменная (не забывая удвоить коэффициенты);

– далее смотрим на оставшиеся симметричные элементы 2-й строки (справа от диагонали) либо 2-го столбца (ниже диагонали) и записываем соответствующие парные произведения (с удвоенными коэффициентами!).

– и, наконец, анализируем правую нижнюю пару симметричных чисел.

Подробное решение и ответ в конце урока.

Знакоопределённость квадратичной формы. Критерий Сильвестра

До сих пор мы рассматривали «внешнее устройство» форм и пришло время изучить их функциональное назначение. Да, по существу, они работают, как функции. Вернёмся к простенькой линейной форме .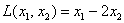

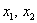
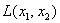
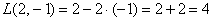
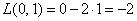
Как отмечалось в начале урока, переменные могут принимать произвольные действительные значения (мы ограничились ими), и каждой такой паре соответствует определённое значение , например:

, и так далее.

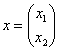
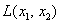
Говоря языком науки, перед нами скалярная функция векторного аргумента, в которой каждому вектору ставится в соответствие определённое число . Обращаю ваше внимание, что сейчас идёт речь не о геометрическом векторе, а о векторе в его алгебраическом понимании.

В зависимости от значений рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы – если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений ).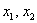

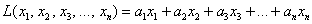
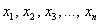
Такая форма называется знакопеременной. И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:

Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной.

– всегда, если только одновременно не равны нулю.

– для любого вектора , кроме нулевого .

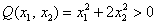
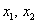
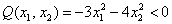
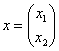
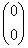
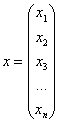
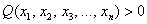
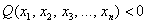
И вообще, если для любого ненулевого вектора , , то квадратичную форму называют положительно определённой; если же – то отрицательно определённой.

Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения 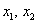, при которых она меньше нуля?

На этот счёт существует теорема: если ВСЕ собственные числа матрицы квадратичной формы положительны*, то она определена положительно. Если все отрицательны – то отрицательно.

* В теории доказано, что все собственные числа действительной симметрической матрицы действительны

Запишем матрицу вышеприведённой формы:
и из уравнения найдём её собственные значения:

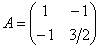
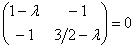
Решаем старое доброе квадратное уравнение: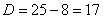

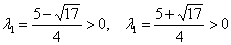
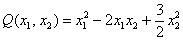
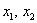
, значит, форма определена положительно, т.е. при любых ненулевых значениях она больше нуля.

Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.

Как быть? Существует более простой путь!

Критерий Сильвестра

Нет, не Сильвестра Сталлоне 🙂 Сначала напомню, что такое угловые миноры матрицы. Это определители 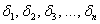которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.

Теперь, собственно, критерий:

1) Квадратичная форма определена положительно тогда и только тогда, когда ВСЕ её угловые миноры больше нуля: .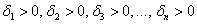

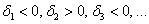
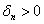
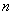
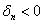
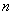
2) Квадратичная форма определена отрицательно тогда и только тогда, когда её угловые миноры знакочередуются, при этом 1-й минор меньше нуля: , , если – чётное или , если – нечётное.

Если в 1-й или 2-й последовательности есть нулевые миноры, то это два особых случая, которые я разберу чуть позже, после того, как мы перещёлкаем более распространённые примеры. При любой другой комбинации плюсов-минусов (и опционально нулей) форма знакопеременна.

Проанализируем угловые миноры матрицы :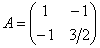

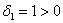
, и это сразу говорит нам о том, что форма не определена отрицательно (отпал пункт 2).

Вывод: все угловые миноры больше нуля, значит, форма 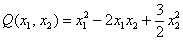определена положительно.

Есть разница с методом собственных чисел? 😉

Запишем матрицу формы 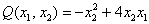из Примера 1:

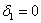
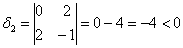
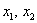
первый её угловой минор , а второй , откуда следует, что форма знакопеременна, т.е. в зависимости от значений , может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.

Возьмём форму 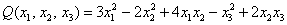и её матрицу из Примера 2:

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём: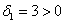
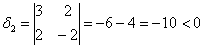
, следовательно, форма точно не отрицательна.

, и точно не положительна (т.к. все угловые миноры должны быть положительными).

Вывод: форма знакопеременна.

Разминочные примеры для самостоятельного решения:

Исследовать квадратичные формы на знакоопределенность

а)

б)

В этих примерах всё гладко (см. конец урока), но на самом деле для выполнения такого задания критерия Сильвестра может оказаться не достаточно.

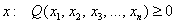
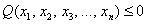
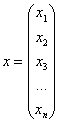
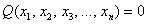
Дело в том, что существуют «краевые» случаи, а именно: если для любого ненулевого вектора , то форма определена неотрицательно, если – то неположительно. У этих форм существуют ненулевые векторы , при которых .

Здесь можно привести такой «баян»:

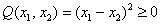
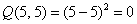
Выделяя полный квадрат, сразу видим неотрицательность формы: , причём, она равна нулю и при любом векторе с равными координатами, например: .

«Зеркальный» пример неположительно определённой формы: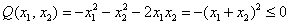

и ещё более тривиальный пример:
– здесь форма равна нулю при любом векторе , где – произвольное число.

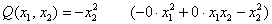
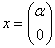
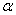
Как выявить неотрицательность или неположительнось формы?

Для этого нам потребуется понятие главных миноров матрицы. Главный минор – это минор, составленный из элементов, которые стоят на пересечении строк и столбцов с одинаковыми номерами. Так, у матрицы существуют два главных минора 1-го порядка:
(элемент находится на пересечении 1-й строки и 1-го столбца);
(элемент находится на пересечении 2-й строки и 2-го столбца),

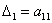
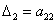
и один главный минор 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца.

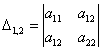
У матрицы «три на три» главных миноров семь, и тут уже придётся помахать бицепсами:
– три минора 1-го порядка,
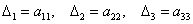
три минора 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца;
– составлен из элементов 1-й, 3-й строки и 1-го, 3-го столбца;
– составлен из элементов 2-й, 3-й строки и 2-го, 3-го столбца,
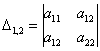
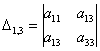
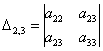
и один минор 3-го порядка:
– составлен из элементов 1-й, 2-й, 3-й строки и 1-го, 2-го и 3-го столбца.
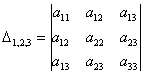
Задание на понимание: записать все главные миноры матрицы .
Сверяемся в конце урока и продолжаем.

Критерий Шварценеггера:

1) Ненулевая* квадратичная форма определена неотрицательно тогда и только тогда, когда ВСЕ её главные миноры неотрицательны (больше либо равны нулю).

* У нулевой (вырожденной) квадратичной формы все коэффициенты равны нулю.

2) Ненулевая квадратичная форма с матрицей 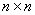определена неположительно тогда и только тогда, когда её:
– главные миноры 1-го порядка неположительны (меньше либо равны нулю);
– главные миноры 2-го порядка неотрицательны;
– главные миноры 3-го порядка неположительны (пошлО чередование);
…
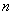
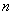
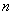
– главный минор -го порядка неположителен, если – нечётное либо неотрицателен, если – чётное.

Если хотя бы один минор противоположного знака, то форма знакопеременна.

Посмотрим, как работает критерий в вышеприведённых примерах:

Составим матрицу 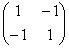формы, и в первую очередь вычислим угловые миноры – а вдруг она определена положительно или отрицательно?

Полученные значения не удовлетворяют критерию Сильвестра, однако второй минор не отрицателен, и это вызывает надобность проверить 2-й критерий (в случае 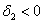2-й критерий будет не выполнен автоматически, т.е. сразу делается вывод о знакопеременности формы).

Главные миноры 1-го порядка:
– положительны,
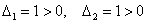
главный минор 2-го порядка:
– не отрицателен.

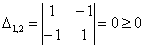
Таким образом, ВСЕ главные миноры не отрицательны, значит, форма неотрицательна.

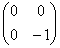
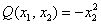
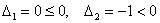
Запишем матрицу формы , для которой, очевидно, не выполнен критерий Сильвестра. Но и противоположных знаков мы тоже не получили (т.к. оба угловых минора равны нулю). Поэтому проверяем выполнение критерия неотрицательности / неположительности. Главные миноры 1-го порядка:
– не положительны,
главный минор 2-го порядка:
– не отрицателен.

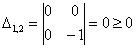
Таким образом, по критерию Шварценеггера (пункт 2), форма определена неположительно.

Теперь во всеоружии разберём более занятную задачку:

Исследовать квадратичную форму на знакоопределенность

Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.

Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры: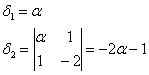

третий определитель я раскрою по 3-й строке:

Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.

Дальнейшее решение удобно разбить на 2 пункта:

1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:

В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством: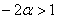

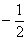
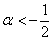
умножим обе его части на , сменив у неравенства знак:
, что противоречит первому неравенству системы.

Таким образом, система несовместна, а значит, форма не может быть положительно определённой ни при каких «альфа», из чего логически и автоматически следует, что она не может быть и неотрицательной.

2) Проведём исследование на отрицательность / неположительнось. По Сильвестру, условию отрицательности формы соответствует следующая система линейных неравенств:

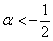
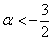
Второе неравенство уже решено: , и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»: .
Таким образом, имеем совместную систему: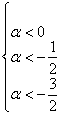

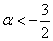
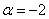
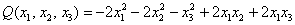
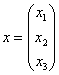
из которой следует, что форма определена отрицательно при . Например, если :
– то при любом ненулевом векторе данная форма будет строго отрицательна.

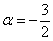
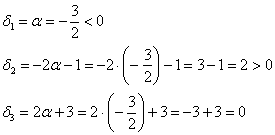
Осталось исследовать «пограничный» случай. Если , то:

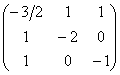
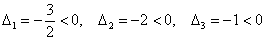
Последнее значение не удовлетворяет 2-му пункту критерия Сильвестра, однако оно равно нулю, что позволяет предположить неположительнось формы. Запишем матрицу формы и проверим критерий Шварценеггера. Главные миноры первого порядка:
– отлично, все миноры неположительны, поэтому проверка продолжается.

Рассчитываем миноры 2-го порядка. Если хотя бы один из них окажется отрицательным, то форма будет знакопеременной:

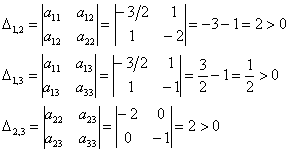
Нет, все миноры неотрицательны, и минор 3-го порядка уже рассчитан:

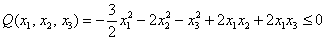
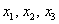
Таким образом, по критерию Шварценеггера (пункт 2), имеет место неположительнось формы, иными словами, , причём, нулю она равна и при некоторых ненулевых значениях .

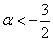
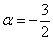
Ответ: при форма определена отрицательно, при неположительно, в остальных случаях форма знакопеременна.

И творческое задание для самостоятельного решения:

Исследовать квадратичную форму на знакоопределенность

И в заключение статьи хочу выразить благодарность Сергею Хохлову, некогда ст. преподавателю МПГУ – за важные замечания и интересные дополнительные примеры, а также Арнольду Шварценеггеру, который сыграл в непривычном для себя амплуа и помог мне ярче объяснить материал 🙂

Как сказал актёр, I’ll be back, и я жду вас на следующем уроке – о каноническом виде квадратичной формы.

Пример 1. Решение: сначала приведём подобные слагаемые: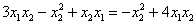

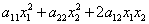
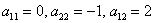
Квадратичная форма двух переменных имеет вид , в данном случае: . Запишем форму в матричном виде:

Проверка:

что и требовалось проверить.

Вычислим дискриминант формы: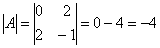

Поскольку 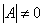, то ранг формы равен двум.

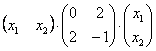
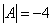
Ответ: , , ранг формы равен двум.

Пример 3. Решение: симметрическая матрица 4*4 определяет квадратичную форму 4 переменных. Коэффициенты главной диагонали 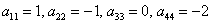, следовательно:

Симметричные коэффициенты 1-й строки: 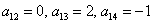, таким образом:

Оставшиеся симметричные элементы 2-й строки: 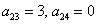, и:

И, наконец,

Ответ:

Пример 4. Решение:

а) запишем матрицу формы: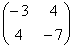

и вычислим её угловые миноры:

Таким образом, по критерию Сильвестра, форма определена отрицательно.

б) запишем матрицу формы: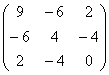

и вычислим её угловые миноры:

Вывод: форма знакопеременна.

Задание на понимание: у данной матрицы четыре главных минора 1-го порядка: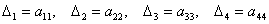
,
шесть главных миноров 2-го порядка: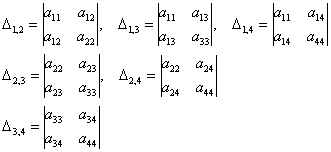

четыре главных минора 3-го порядка: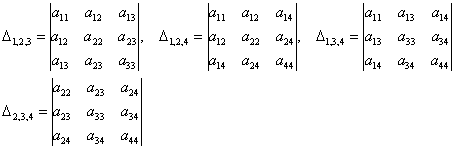

и один главный минор 4-го порядка, равный определителю матрицы.

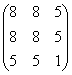
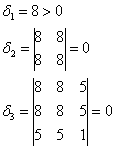
Пример 5*. Решение: запишем матрицу формы и вычислим её угловые миноры:

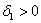
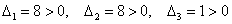
Таким образом, форма не удовлетворяет критерию Сильвестра, однако, может оказаться неотрицательной (т.к. и остальные миноры нулевые). Для этого все главные миноры должны быть неотрицательны. Главные миноры 1-го порядка:
.
Вычислим главные миноры 2-го порядка:

– среди главных миноров встретился отрицательный, следовательно, форма не удовлетворяет критерию неотрицательности.

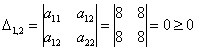
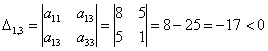
Ответ: форма знакопеременна.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Источник