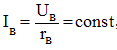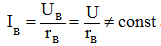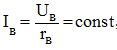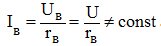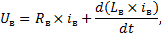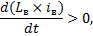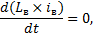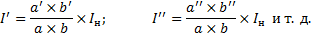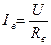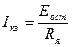Почему внешняя характеристика генератора параллельного возбуждения имеет более падающий вид чем
Генератор с параллельным возбуждением. Внешняя характеристика.
Внешняя характеристика U=f (I) при rв=const и n=const (рисунок 1) показывает влияние изменения нагрузки на напряжение генератора. При этом ток возбуждения не регулируется с помощью регулировочного реостата. Следует учесть, что при независимом возбуждении
а при параллельном возбуждении
Последнее равенство означает, что при снятии внешней характеристики ток возбуждения генератора изменяется пропорционально напряжению на генераторе. Таким образом, уменьшение напряжения генератора параллельного возбуждения при увеличении его нагрузки вызывается не только размагничивающим действием реакции якоря и падением напряжения в цепи якоря, но и уменьшением тока возбуждения. Поэтому внешняя характеристика генератора параллельного возбуждения (рисунок 1 ) (кривая 1) располагается ниже внешней характеристики генератора независимого возбуждения (кривая 2).
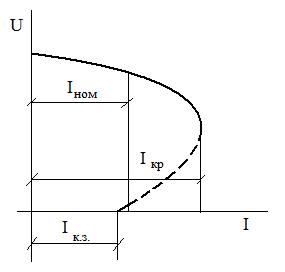
В генераторе параллельного возведения ток нагрузки I будет увеличиваться только до определенного критического значения Iкр=(2. 2,5) Iн, после чего он начнет уменьшаться до Iко
Характеристики генератора параллельного возбуждения
Характеристика холостого хода U0=f(Iв) при I=0 и n=const. В процессе самовозбуждения в генераторах параллельного возбуждения Ia=Iв, причем Iв=(0,02…0,03)Iн. Поэтому можно пренебречь реакцией якоря и падением напряжения в обмотке якоря и считать, что между характеристиками холостого хода генератора параллельного возбуждения и независимого возбуждения практически нет разницы. Следует учесть, что эта характеристика может быть снята только в одном квадранте, так как процесс самовозбуждения в данном генераторе может протекать только в одном направлении при согласном действии остаточного магнитного потока и потока, создаваемого током возбуждения, причем на прямолинейном участке характеристики напряжение генератора не удается регулировать как у генератора независимого возбуждения, что определяет меньший диапазон регулирования его напряжения.
Нагрузочная характеристика U=f(Iв) при I=const и n=const. Нагрузочные характеристики генератора параллельного возбуждения практически совпадают с характеристиками генератора независимого возбуждения, так как увеличение тока Iа на величину тока возбуждения при параллельном возбуждении не может оказать заметного влияния на напряжение генератора.
Внешняя характеристика U=f(I) при rв=const и n=const (рисунок 1) показывает влияние изменения нагрузки на напряжение генератора. При этом ток возбуждения не регулируется с помощью регулировочного реостата. Следует учесть, что при независимом возбуждении
а при параллельном возбуждении
Последнее равенство означает, что при снятии внешней характеристики ток возбуждения генератора изменяется пропорционально напряжению на генераторе. Таким образом, уменьшение напряжения генератора параллельного возбуждения при увеличении его нагрузки вызывается не только размагничивающим действием реакции якоря и падением напряжения в цепи якоря, но и уменьшением тока возбуждения. Поэтому внешняя характеристика генератора параллельного возбуждения (рисунок 1 ) (кривая 1) располагается ниже внешней характеристики генератора независимого возбуждения (кривая 2).
Генераторы параллельного возбуждения
Определение. Генераторами параллельного возбуждения называют генераторы, обмотка возбуждения которых питается от ЭДС обмотки якоря и подключена к выводам якоря машины параллельно цепи нагрузки.
Схема генератора параллельного возбуждения. Схема изображена на рис. 1.20. Ток якоря IЯ = I + IВ у щеток разветвляется на ток нагрузкиI и ток возбуждения IВ . Обычно ток возбуждения невелик и составляет (0,01-0,05) IЯ.НОМ . Последовательно с обмоткой возбуждения включается реостат RP для регулирования возбуждения. Реостат позволяет изменять ток возбуждения и, следовательно, напряжение генератора.
Характеристика холостого хода генератора с самовозбуждением всегда снимается при независимом возбуждении (обмотка возбуждения отключается от якоря и запитывается от постороннего источника) и поэтому аналогична характеристике холостого хода генератора с независимым возбуждением.
Самовозбуждение генератора. Так как обмотка возбуждения подключена к выводам якоря, то важное значение имеет процесс первоначального возникновения ЭДС, называемый процессом самовозбуждения.
Рассмотрим процесс самовозбуждения при отключенной нагрузке генератора, т.е. при холостом ходе.
Магнитная цепь машины имеет небольшой остаточный магнитный поток (примерно 2-3% номинального). При вращении якоря в поле остаточного потока в нем наводится небольшая ЭДС, вызывающая некоторый ток в обмотке возбуждения. При соответствующем направлении он увеличивает остаточный магнитный поток, ЭДС в якоре возрастает и процесс развивается лавинообразно до тех пор, пока не будет ограничен насыщением магнитной цепи.
Однако процесс самовозбуждения может развиваться только при определенных условиях, называемых условиями самовозбуждения. Выясним эти условия. Уравнение второго закона Кирхгофа для цепи возбуждения имеет вид: Е + еL= (Rв + Rя)iв, где еL = – d (Liв) /dt – ЭДС самоиндукции цепи возбуждения, возникающая при нарастании тока возбуждения;
L – суммарная индуктивность обмоток возбуждения и якоря; Rв — сумма сопротивлений обмотки возбуждения и регулировочного реостата.
Так как Rя « Rв, то уравнение принимает вид:
Eя=Rв iв +
Покажем на графике характеристику холостого хода Е = f (Iв) и характеристику цепи возбуждения – прямую Uв = Rв Iв
(рис. 1.21). Отрезок аб, равный Е – Rв Iв = d (Liв) /dt, пропорционален ЭДС самоиндукции цепи возбуждения. Из графика следует, что в точке в пересечения характеристик d (Liв) /dt = 0 рост тока возбуждения прекращается Uв = E и процесс самовозбуждения заканчивается. Положение точки в, называемой рабочейточкой, зависит от сопротивления цепи возбуждения Rв » tgα. Чем оно больше, тем прямая Uв = f (Iв) идет круче и рабочая точка перемещается влево. При некотором сопротивлении цепи возбуждения Rв, кр = tg αкр, называемом критическим, напряжение на выводах генератора близко к остаточной ЭДС Ео и генератор не возбуждается.
Из сказанного вытекают условия, при которых генератор должен возбуждаться:
Ø наличие остаточной намагниченности;
Ø совпадение по направлению остаточного магнитного поля и поля, создаваемого обмоткой возбуждения (несовпадение полей может быть при неправильном подключении выводов обмотки возбуждения или при несоответствующем направлении вращения якоря);
Ø сопротивление цепи возбуждения должно быть меньше критического;
Ø скорость вращения якоря должна быть выше критической скорости.
Внешняя характеристика. Внешняя характеристика генератора параллельного возбуждения U = f (I) при Rв = const и n = nном = const (рис. 1.18, кривые 2 и 2а) отличается от внешней характеристики генератора независимого возбуждения более резким снижением напряжения при увеличении нагрузки. Это объясняется следующим образом: уменьшение напряжения по тем же причинам, что и у генератора независимого возбуждения, приводит к уменьшению тока возбуждения, дополнительному уменьшению ЭДС генератора. При номинальной нагрузке снижение напряжения относительно напряжения холостого хода составляет 10-18%.
Регулировочная характеристика. Регулировочная характеристика генератора Iв = f (I) при U = Uном = const и n = nном = const аналогична регулировочной характеристике генератора независимого возбуждения (рис. 1.19, кривая 2), но идет несколько круче, что объясняется более значительным уменьшением напряжения генератора.
Генераторы параллельного возбуждения
Самовозбуждение генератора параллельного возбуждения
Самовозбуждение генератора параллельного возбуждения происходит при соблюдении следующих условий: 1) наличия остаточного магнитного потока полюсов; 2) правильного подключения концов обмотки возбуждения или правильного направления вращения. Кроме того, сопротивление цепи возбуждения Rв при данной скорости вращения n должно быть ниже некоторого критического значения или скорость вращения при данном Rв должна быть выше некоторого критического значения.
Для самовозбуждения достаточно, чтобы остаточный поток составлял 2 – 3% от номинального. Остаточный поток такого значения практически всегда имеется в уже работавшей машине. Вновь изготовленную машину или машину, которая по каким-либо причинам размагнитилась, необходимо намагнитить, пропуская через обмотку возбуждения ток от постороннего источника.
При соблюдении необходимых условий процесс самовозбуждения протекает следующим образом. Небольшая электродвижущая сила (э. д. с.), индуктируемая в якоре остаточным магнитным потоком, вызывает в обмотке возбуждения малый ток iв. Этот ток вызывает увеличение потока полюсов, а следовательно, увеличение э. д. с., которая обуславливает дальнейшее увеличение iв, и так далее. Такой лавинообразный процесс самовозбуждения продолжается до тех пор, пока напряжение генератора не достигнет установившегося значения.
Если подключение концов обмотки возбуждения или направление вращения неправильны, то возникает ток iв обратного направления, вызывающий ослабление остаточного потока и уменьшение э. д. с., вследствие чего самовозбуждение невозможно. Тогда необходимо переключить концы обмотки возбуждения или изменить направление вращения. В соблюдении этих условий можно убедиться, следя с помощью вольтметра с малым пределом измерения за напряжением якоря при замыкании и размыкании цепи возбуждения.
Полярность зажимов генератора при самовозбуждении определяется полярностью остаточного потока. Если при заданном направлении вращения полярность генератора необходимо изменить, то следует перемагнитить машину путем подачи тока в обмотку возбуждения от постороннего источника.
Рисунок 1. Самовозбуждение генератора параллельного возбуждения при различных сопротивлениях цепи возбуждения (а) и при различных скоростях вращения (б)
Рассмотрим подробнее процесс самовозбуждения при холостом ходе.
На рисунке 1, а кривая 1 представляет собой характеристику холостого хода (х. х. х.), а прямая 2 – так называемую характеристику цепи возбуждения или зависимость Uв = Rв × iв, где Rв = const – сопротивление цепи возбуждения, включая сопротивление регулировочного реостата.
В процессе самовозбуждения iв ≠ const и напряжение на концах цепи возбуждения
где Lв – индуктивность цепи возбуждения.
Напряжение якоря при холостом ходе (I = 0)
изображается на рисунке 1, а кривой 1. Так как ток iв мал, то практически Uа = Eа.
Но в генераторе параллельного возбуждения (смотрите рисунок 1, б, в статье «Общие сведения о генераторах постоянного тока») Uа = Uв. Поэтому разность ординат кривой 1 и прямой 2 на рисунке 1, а составляет d(Lвiв)/dt и характеризует скорость и направление изменения iв. Если прямая 2 проходит ниже кривой 1, то
iв растет и машина самовозбуждается до напряжения, соответствующего на рисунке 1, а точке пересечения кривой 1 и прямой 2, в которой
и рост iв поэтому прекращается.
Из рассмотрения рисунка 1, а следует, что нарастание iв и, следовательно, Uа сначала происходит медленно, затем ускоряется и к концу процесса вновь замедляется. Начавшийся процесс самовозбуждения прекращается или ограничивается в точке а’ вследствие криволинейности х. х. х. При отсутствии насыщения Uа теоретически возросло бы до Uа = ∞.
Если Rв увеличить, то вместо прямой 2 получим прямую 3 (рисунок 1, а). Процесс самовозбуждения при этом замедляется и напряжение машины, определяемое точкой а’’, будет меньше. При дальнейшем увеличение Rв получим прямую 4, касательную к кривой 1. При этом машина будет находиться на грани самовозбуждения: при небольших изменениях n или Rв (например, вследствие нагревания) машина может развивать небольшое напряжение или терять его. Значение Rв, соответствующее прямой 4, называется критическим сопротивлением цепи возбуждения (Rв.кр). При Rв > Rв.кр (прямая 5) самовозбуждение невозможно и напряжение машины определяется остаточным потоком.
Из сказанного следует, что генератор параллельного возбуждения может работать только при наличии определенного насыщения магнитной цепи. Посредством изменения Rв можно регулировать U до значения U = Uмин., соответствующего началу колена кривой х. х. х. В машинах обычного исполнения Uмин. = (0,65 – 0,75)Uн.
Э. д. с. Eа ∼ n, и для разных значений n1 > n2 > n3 получим х. х. х., изображенные на рисунке 1, б кривыми 1, 2, 3. Из этого рисунка видно, что при небольшом значении Rв в случае кривой 1 имеется устойчивое самовозбуждение, при кривой 2 машина находится на грани самовозбуждения и при кривой 3 самовозбуждение невозможно. Поэтому для каждого данного значения Rв существует такое значение скорости вращения n = nкр. (кривая 2 на рисунке 1, б), ниже которого самовозбуждение невозможно. Такое значение n = nкр. называется критической скоростью вращения.
| Рисунок 3. Характеристика холостого хода генератора параллельного возбуждения |
В некоторых случаях требуется, чтобы U генератора параллельного возбуждения можно было регулировать в широких пределах, например Uн : Uмин. = 5 : 1 или даже U : Uмин. = 10 : 1 (возбудители синхронных машин). Тогда кривая х. х. х. должна искривляться уже в своей начальной части. С этой целью в необходимых случаях в магнитной цепи выполняют участки с ослабленным сечением (магнитные мостики насыщения) в виде прорезей в листах сердечников полюсов (рисунок 2, а), выступов в верхней части этих листов (рисунок 2, б) и тому подобных. В таких мостиках происходит концентрация магнитного потока, и их насыщение наступает уже при малых потоках.
Характеристика холостого хода
Характеристика холостого хода U = f(iв) при I = 0 и n = const при параллельном возбуждении может быть снята только в одном квадранте (рисунок 3) путем регулирования iв с помощью регулировочного реостата в цепи возбуждения (смотрите рисунок 1, б, в статье «Общие сведения о генераторах постоянного тока»). Так как ток iв мал, то U ≈ Eа, и характер кривой х. х. х. у генератора с параллельным возбуждением будет таким же, как и у генератора с независимым возбуждением.
Характеристика короткого замыкания
Характеристика короткого замыкания I = f(iв) при U = 0 и n = const для генератора параллельного возбуждения может быть снята только при питании обмотки возбуждения от постороннего источника, как и для генератора независимого возбуждения, так как при самовозбуждении при U = 0 ток цепи возбуждения также равен нулю iв = 0.
Внешняя характеристика
Внешняя характеристика U = f(I) генератора параллельного возбуждения снимается при Rв = const и n = const, то есть без регулирования в цепи возбуждения, при естественных условиях работы. Вследствие этого к двум причинам падения напряжения, указанным для генератора независимого возбуждения (смотрите статью «Генераторы независимого возбуждения»), прибавляется третья – уменьшение iв при уменьшении U. В результате внешняя характеристика генератора параллельного возбуждения (рисунок 4, кривая 1) падает круче, чем у генератора независимого возбуждения (кривая 2). Поэтому номинальное изменение напряжения (смотрите определение в статье «Генераторы независимого возбуждения») у генератора параллельного возбуждения больше и составляет дельта Uн% = 10 – 20 %.
| Рисунок 4. Внешние характеристики генераторов параллельного (1) и независимого (2) возбуждения |
Работа машины на ветви аб характеристики несколько неустойчива и имеется склонность самопроизвольного изменения I. Ток Iк.уст. в некоторых случаях может быть больше Iн.
Построение внешней характеристики генератора параллельного возбуждения с помощью х. х. х. и характеристического треугольника показано на рисунке 5, где 1 – кривая х. х. х.; 2 – характеристика цепи возбуждения Uв = Rв × iв при заданном Rв = const и 3 – построенная кривая внешней характеристики.
Перенеся все эти точки в левый квадрант диаграммы рисунка 5 и соединив их плавной кривой, получим искомую характеристику 3. С учетом нелинейной зависимости катета аб треугольника от I опытная зависимость U = f(I) имеет характер, показанный на рисунке 5 слева штриховой линией.
| Рисунок 5. Построение внешней характеристики генератора параллельного возбуждения с помощью характеристики холостого хода и характеристического треугольника |
Хотя установившийся ток короткого замыкания генератора параллельного возбуждения невелик, внезапное короткое замыкание на зажимах этого генератора практически столь же опасно, как и у генератора независимого возбуждения. Объясняется это тем, что вследствие большой индуктивности обмотки возбуждения и индуктирования вихревых токов в массивных частях магнитной цепи уменьшение магнитного потока полюсов происходит медленно. Поэтому быстро нарастающий ток якоря достигает значений Iк = (5 – 15)Iн.
Регулировочная и нагрузочная характеристика
Регулировочная характеристика iв = f(I) при U = const и n = const и нагрузочная характеристика U = f(iв) при I = const и n = const снимаются так же, как и у генератора независимого возбуждения. Так как iв и Rа × iв малы, то падение напряжения от iв в цепи якоря практически не оказывает влияния на напряжение на зажимах генератора. Поэтому указанные характеристики получаются практически такими же, как и у генератора независимого возбуждения. Построение этих характеристик с помощью х. х. х. и характеристического треугольника также производится аналогичным образом.
В заключение можно отметить, что характеристики и свойства генераторов независимого и параллельного возбуждения мало отличаются друг от друга. Единственное заметное отличие заключается в некотором расхождении внешних характеристик в пределах от I = 0 до I = Iн. Более сильное расхождение этих характеристик при I намного больше Iн не имеет значения, поскольку в таких режимах машины в условиях эксплуатации, как правило, не работают.
Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.
Внешняя характеристика генератора с параллельным возбуждением.
Эта характеристика отражает зависимость напряжения на зажимах генератора от тока нагрузки:
Рис.14.2.Внешняя характеристика генератора с параллельным возбуждением.
При увеличении нагрузки напряжение на зажимах генератора под влиянием реакции якоря и падения напряжения в цепи якоря уменьшается. Снижение напряжения вызывает уменьшение тока возбуждения
В свою очередь, уменьшение Iв вызывает ослабление основного магнитного потока, а следовательно, уменьшение э.д.с. и напряжения на зажимах генератора.
С понижением напряжения происходит дальнейшее уменьшение Iв.
При этом магнитная система генератора постепенно размагничивается. В генераторе с параллельным возбуждением ток нагрузки увеличивается лишь до определенного критического значения Iкр, превышающего номинальное не более чем в 2—2,5 раза.
Величина тока нагрузки зависит от двух факторов: величины напряжения генератора и сопротивления нагрузки. При увеличении тока нагрузки уменьшается напряжение на зажимах генератора (рис. 14.2.).
В начале, когда магнитная система насыщена, размагничивание идет медленно и напряжение U изменяется незначительно, вследствие чего ток в цепи якоря увеличивается. Однако при дальнейшем увеличении тока степень насыщения магнитной системы резко уменьшается, и напряжение начинает быстро падать. Преобладающим будет уже не уменьшение сопротивления цепи, а понижение напряжения.
Поэтому ток, достигнув критического значения, начнет уменьшаться. При к.з Iв =0, так как U = 0.Величина Iк.з. будет определяться только величиной э.д.с. остаточной индукции:
Таким образом, к.з, вызванное постепенным уменьшением сопротивления нагрузки, не опасно для генератора параллельного возбуждения.
Но при внезапном коротком замыкании магнитная система генератора не успевает сразу размагнититься, и ток Iк.з. достигает опасных для машины значений. При таком резком возрастании тока па валу генератора возникает значительный тормозящий момент, а на коллекторе появляется сильное искрение, переходящее в круговой огонь.
Дата добавления: 2014-12-24 ; просмотров: 2136 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ