Почему при последовательном соединении ток источника меньше чем при параллельном

Последовательное и параллельное соединения проводников

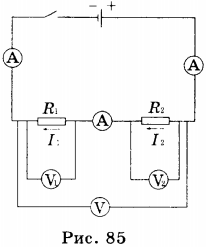
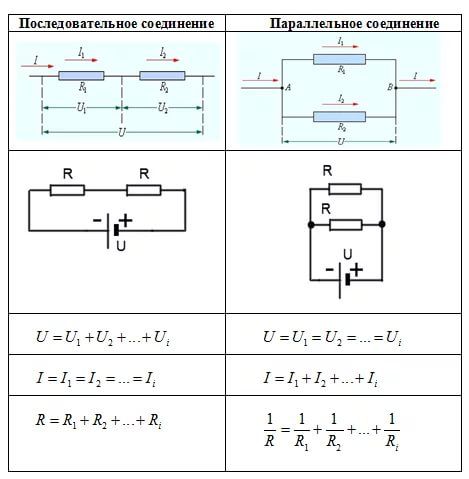
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).

Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.

При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: ​ \( I_1=I_2=I \) ​.

Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: ​ \( R_1=R_2=R \) ​. Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.

По закону Ома напряжение на каждом проводнике равно: ​ \( U_1=IR_1 \) ​, ​ \( U_2=IR_2 \) ​, а общее напряжение равно ​ \( U=I(R_1+R_2) \) ​. Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: ​ \( U=U_1+U_2 \) ​.

Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.

2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.

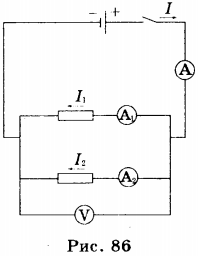
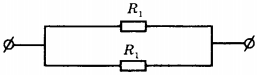
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).

Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: ​ \( U_1=U_2=U \) ​.

При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: ​ \( I=I_1+I_2 \) ​.

При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление ​ \( r \) ​, то их общее сопротивление равно: ​ \( R=r/2 \) ​. Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.

Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

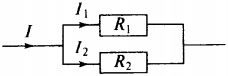
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Напряжения на резисторах соответственно ​ \( U_1 \) ​ и ​ \( U_2 \) ​.

По какой из формул можно определить напряжение U на участке АВ?

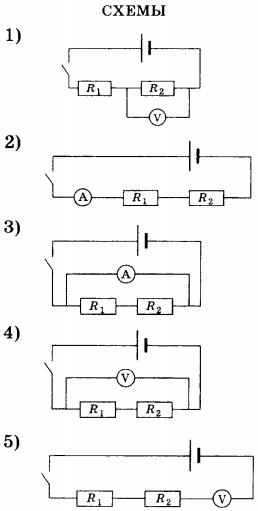
2. На рисунке изображёна схема электрической цепи, содержащая два параллельно включённых резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

1) ​ \( I=I_1=I_2 \) ​
2) \( I=I_1+I_2 \)
3) \( U=U_1+U_2 \)
4) \( R=R_1+R_2 \)

3. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением R> и R2. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

4. На рисунке изображена схема электрической цепи. В эту цепь последовательно включены два резистора сопротивлением ​ \( R_1 \) ​ и ​ \( R_2 \) ​. Какое из приведённых ниже соотношений справедливо для такого соединения резисторов?

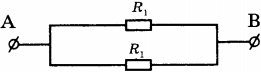
5. На рисунке изображена схема электрической цепи. В эту цепь параллельно включены два одинаковых резистора сопротивлением ​ \( R_1 \) ​. По какой из формул можно определить общее сопротивление цепи ​ \( R \) ​?

6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов ​ \( R_1 \) ​ и ​ \( R_2 \) ​ равны. Чему равно сопротивление каждого резистора?

1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом

7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?

1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом

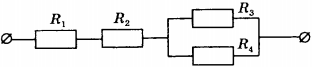
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если ​ \( R_1 \) ​ = 1 Ом, ​ \( R_2 \) ​ = 10 Ом, ​ \( R_3 \) ​ = 10 Ом, ​ \( R_4 \) ​ = 5 Ом?

1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом

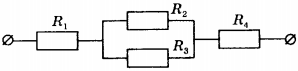
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?

1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом

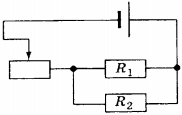
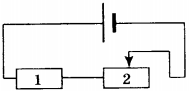
10. Если ползунок реостата (см. схему) переместить влево, то сила тока

1) в резисторе ​ \( R_1 \) ​ уменьшится, а в резисторе ​ \( R_2 \) ​ увеличится
2) увеличится в обоих резисторах
3) в резисторе ​ \( R_1 \) ​ увеличится, а в резисторе ​ \( R_2 \) ​ уменьшится
4) уменьшится в обоих резисторах

11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?

Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1

ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) ​ и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) ​ и \( R_2 \)

Часть 2

13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов ​ \( R_1 \) ​ = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?

Источник

Сила тока при последовательном соединении

В электрических цепях используются различные типы соединений. Основными являются последовательные, параллельные и смешанные схемы подключений. В первом случае используется несколько сопротивлений, соединенных в единую цепочку друг за другом. То есть, начало одного резистора соединяется с концом второго, а начало второго – с концом третьего и так далее, до любого количества сопротивлений. Сила тока при последовательном соединении будет одинаковой во всех точках и на всех участках. Для определения и сравнения других параметров электрической цепи, следует рассматривать и остальные виды соединений, обладающие собственными свойствами и характеристиками.

Последовательное и параллельное соединение сопротивлений

Любая нагрузка обладает сопротивлением, препятствующим свободному течению электрического тока. Его путь проходит от источника тока, через проводники к нагрузке. Для нормального прохождения тока, проводник должен обладать хорошей проводимостью и легко отдавать электроны. Это положение пригодится далее при рассмотрении вопроса, что такое последовательное соединение.

В большинстве электрических цепей применяются медные проводники. Каждая цепь содержит приемники энергии – нагрузки, обладающие различными сопротивлениями. Параметры соединения лучше всего рассматривать на примере внешней цепи источника тока, состоящей из трех резисторов R1, R2, R3. Последовательное соединение предполагает поочередное включение этих элементов в замкнутую цепь. То есть начало R1 соединяется с концом R2, а начало R2 – с концом R3 и так далее. В такой цепочке может быть любое количество резисторов. Эти символы используют в расчетах последовательные и параллельные соединения.

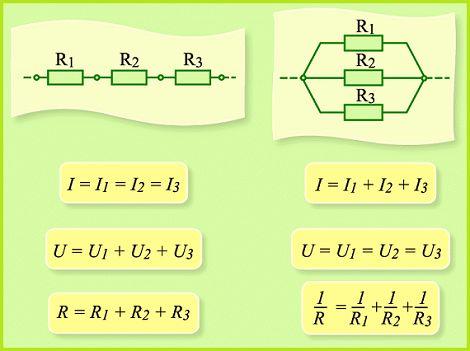
Сила тока на всех участках будет одинаковой: I = I1 = I2 = I3, а общее сопротивление цепи составит сумму сопротивлений всех нагрузок: R = R1 + R2 + R3. Остается лишь определить, каким будет напряжение при последовательном соединении. В соответствии с законом Ома, напряжение представляет собой силу тока и сопротивления: U = IR. Отсюда следует, что напряжение на источнике тока будет равно сумме напряжений на каждой нагрузке, поскольку ток везде одинаковый: U = U1 + U2 + U3.

При постоянном значении напряжения, ток при последовательном соединении будет находиться в зависимости от сопротивления цепи. Поэтому при изменении сопротивления хотя-бы на одной из нагрузок, произойдет изменение сопротивления во всей цепи. Кроме того, изменятся ток и напряжение на каждой нагрузке. Основным недостатком последовательного соединения считается прекращение работы всех элементов цепи, при выходе из строя даже одного из них.

Совершенно другие характеристики тока, напряжения и сопротивления получаются при использовании параллельного соединения. В этом случае начала и концы нагрузок соединяются в двух общих точках. Происходит своеобразное разветвление тока, что приводит к снижению общего сопротивления и росту общей проводимости электрической цепи.

Для того чтобы отобразить эти свойства, вновь понадобится закон Ома. В данном случае сила тока при параллельном соединении и его формула будет выглядеть так: I = U/R. Таким образом, при параллельном соединении n-го количества одинаковых резисторов, общее сопротивление цепи будет в n раз меньше любого из них: Rобщ = R/n. Это указывает на обратно пропорциональное распределение токов в нагрузках по отношению к сопротивлениям этих нагрузок. То есть, при увеличении параллельно включенных сопротивлений, сила тока в них будет пропорционально уменьшаться. В виде формул все характеристики отображаются следующим образом: сила тока – I = I1 + I2 + I3, напряжение – U = U1 = U2 = U3, сопротивление – 1/R = 1/R1 + 1/R2 + 1/R3.

При неизменном значении напряжения между элементами, токи в этих резисторах не имеют зависимости друг от друга. Если один или несколько резисторов будут выключены из цепи, это никак не повлияет на работу других устройств, остающихся включенными. Данный фактор является основным преимуществом параллельного соединения электроприборов.

В схемах обычно не используется только последовательное соединение и параллельное соединение сопротивлений, они применяются в комбинированном виде, известном как смешанное соединение. Для вычисления характеристик таких цепей применяются формулы обоих вариантов. Все расчеты разбиваются на несколько этапов, когда вначале определяются параметры отдельных участков, после чего они складываются и получается общий результат.

Законы последовательного и параллельного соединения проводников

Основным законом, применяемым при расчетах различных видов соединений, является закон Ома. Его основным положением является наличие на участке цепи силы тока, прямо пропорциональной напряжению и обратно пропорциональной сопротивлению на данном участке. В виде формулы этот закон выглядит так: I = U/R. Он служит основой для проведения расчетов электрических цепей, соединяемых последовательно или параллельно. Порядок вычислений и зависимость всех параметров от закона Ома наглядно показаны на рисунке. Отсюда выводится и формула последовательного соединения.

Более сложные вычисления с участием других величин требуют применения правила Кирхгофа. Его основное положение заключается в том, что несколько последовательно соединенных источников тока, будут обладать электродвижущей силой (ЭДС), составляющей алгебраическую сумму ЭДС каждого из них. Общее сопротивление этих батарей будет состоять из суммы сопротивлений каждой батареи. Если выполняется параллельное подключение n-го количества источников с равными ЭДС и внутренними сопротивлениями, то общая сумма ЭДС будет равно ЭДС на любом из источников. Значение внутреннего сопротивления составит rв = r/n. Эти положения актуальны не только для источников тока, но и для проводников, в том числе и формулы параллельное соединение проводников.

В том случае, когда ЭДС источников будет иметь разное значение, для расчетов силы тока на различных участках цепи применяются дополнительные правила Кирхгофа.

Источник

Последовательное и параллельное соединение источников питания

Что такое источник питания

Источник питания — это специальное устройство, которое может генерировать ЭДС. К источникам питания постоянного тока можно отнести аккумуляторы, батарейки, различные генераторы постоянного тока (лабораторный блок питания), элементы Пельтье и тд. То есть это все те устройства, которые создают ЭДС.

Источник питания на примере гидравлики

Давайте рассмотрим водобашню, в которой есть автоматическая подача воды. То есть сколько бы мы не потребляли воды из башни, ее уровень воды будет неизменным.

Схематически это будет выглядеть вот так:

Башню с автоматической подачей воды можно считать источником питания. В химических же источниках питания происходит разряд, что ведет к тому, что уровень напряжения понижается при длительной работе. А что такое напряжение по аналогии с гидравликой? Это тот же самый уровень воды)

Давайте отпилим у водобашни верхнюю часть для наглядности. У нас получится цилиндр, который заполнен водой. Возьмем за точку отсчета уровень земли. Пусть он у нас будет равняться нулю.

Теперь вопрос на засыпку. В каком случае давление на дно будет больше? Когда в башне немного воды

либо когда башня полностью залита водой так, что даже вода выходит за ее края

Разумеется, когда башня наполнена только наполовину водой, на дне башни давление меньше, чем тогда, когда в башне воды под завязку.

Думаю, не надо объяснять, что если в башне вообще нет воды, то никакого давления на дне башни не будет.

По тому же самому принципу работает батарейка или аккумулятор

На электрических схемах ее обозначение выглядит примерно вот так:

Также, чтобы получить необходимое напряжение, одноэлементные источники питания соединяют последовательно. На схеме это выглядит вот так:

Любой аккумулятор или источник постоянного тока имеет два полюса: «плюс» и «минус». Минус — это уровень земли, как в нашем примере с водобашней, а плюс — это напряжение, по аналогии с гидравликой это и будет тот самый уровень воды.

Последовательное соединение источников питания

Теперь давайте представим вот такую ситуацию. Что будет, если в нашей обрезанной водобашне полной воды добавим еще одну такую же сверху полную воды? Схематически это будет выглядеть примерно вот так:

Как вы думаете, уменьшится давление на землю, или увеличится? Понятное дело, что увеличится! Да еще и ровно в два раза! Почему так произошло? Уровень воды стал выше, следовательно, давление на дно увеличилось.

Если «минус» одной батарейки соединить с «плюсом» другой батарейки, то их общее напряжение суммируется.

Полностью заряженная батарейка будет выглядеть как башня, полностью залитая водой с учетом того, что работает насос автоматической подачи воды. По аналогии, насос — это ЭДС.

Наполовину разряженная батарейка будет уже выглядеть примерно вот так:

Можно сказать, насос уже не справляется.

Батарейка посаженная в «ноль» будет выглядеть вот так:

Насос автоматической подачи воды сломался.

Естественно, что если вы соедините полностью заряженную и наполовину дохлую батарейку последовательно, то их общее напряжение будет выглядеть примерно вот так:

Давайте все это продемонстрируем на практике. Итак, у нас есть 2 литий-ионных аккумулятора. Я их пометил цифрами 1 и 2. С плюса каждого аккумулятора я вывел красный провод, а с минуса — черный.

Давайте замеряем напряжение аккумулятора под №1 с помощью мультиметра. Как это сделать, я еще писал в статье Как измерить ток и напряжение мультиметром.

На первом аккумуляторе у нас напряжение 3,66 Вольт. Это типичное значение литий-ионного аккумулятора.

Таким же способом замеряем напряжение на аккумуляторе №2

О, как совпало). Те же самые 3,66 Вольт.

Для того, чтобы соединить последовательно эти аккумуляторы, нам надо сделать что-то подобное:

Также как и в башнях, нам надо соединить основание одной башни с верхушкой другой башни. В источниках питания, типа аккумуляторов или батареек, нам надо соединить минус одной батарейки с плюсом другой. Так мы и сделаем. Соединяем плюс одной батарейки с минусом другой и получаем… сумму напряжений каждой батарейки! Как вы помните, на первой батарейке у нас было напряжение 3,66 В, на второй тоже 3,66 В. 3,66+3,6=7,32 В.

Мультиметр показывает 7,33 В. 0,01В спишем на погрешность измерений.

Это свойство прокатывает не только с двумя аккумуляторами, но также с их бесконечным множеством. Думаю, не стоит говорить, что если выставить в ряд штук 100 таких аккумуляторов, соединить последовательно и коснуться крайних полюсов голыми руками, то все это может завершиться даже летальным исходом.

Параллельное соединение источников питания

Но что будет, если источники питания соединить параллельно? Давайте же рассмотрим это с точки зрения той же самой гидравлики. Имеем те же самые башни, в которых воды до самых краев:

Нет, здесь мы не будет извращаться. Мы просто соединим наши башни у самого основания трубой:

Давление на дно у каждой башни изменится? Думаю, нет. Оно останется таким же, как в одной из башен. А что поменялось? Поменялся просто объем воды. Ее стало в 2 раза больше.

Но вы можете сказать, что в первом случае у нас тоже воды стало в 2 раза больше!

Да, все оно так, но здесь важное значение имеет именно то, что давление на дно башни изменилось и стало также в два раза больше. Если сделать врезку одинакового диаметра прямо у подножия водобашни, то в случае, когда водобашни стоят одна на другой сила потока воды будет в два раза быстрее, чем если бы мы делали точно такую же врезку на картинке, где мы соединяли водобашни трубой. Более подробно эту мысль я еще озвучивал в статье про Закон Ома.

Если всю эту мысль спроецировать на наши источники питания, то получается, что при последовательном соединении у нас суммировалась напряжение, а при параллельном должна суммироваться сила тока. Но это не значит, что нагрузка, которая кушала, к примеру, 1 Ампер, после того, как мы ее цепанем к двум параллельным источникам питания, будет кушать 2 Ампера. При параллельном соединении у нас напряжение остается таким же, а вот емкость батарей увеличивается. Но нагрузка все равно будет кушать тот же самый 1 Ампер, иначе бы все это противоречило закону Ома.

Настало время все это рассмотреть на реальном примере. Итак, замеры мы уже делали. Осталось соединить два источника питания параллельно, в нашем случае это аккумуляторы li-ion:

Как вы видите, напряжение не изменилось.

При параллельном соединении источников питания должно соблюдаться условие, что на них должно быть одинаковое напряжение.

Вот сами подумайте, что может произойти, если одна из башен будет пустая?

Думаю, нетрудно догадаться, что вода из одной башни будет перетекать в другую башню, пока их уровень не выровняется (закон сообщающихся сосудов), если у одной башни сломался насос и она пустая.

То же самое и с источниками питания. Нельзя соединять источники питания разных напряжений параллельно. Это чревато тем, что вы убьете здоровые аккумуляторы, а дохлые так и останутся дохлыми или чуток зарядятся. Если разница между напряжениями аккумулятора большая, то в такой цепи может течь бешеная сила тока, которая вызовет нагрев и даже возгорание аккумуляторов.

Нельзя соединять источники питания разных напряжений параллельно

Последовательно-параллельное соединение источников питания

А кто вам мешает соединять аккумуляторы или батарейки сразу и последовательно и параллельно? Но разве так можно? Можно). На примере с водобашнями это может выглядеть вот так:

Здесь мы видим две башни, каждая из которых состоит их двух башенок, и эти две большие башни соединены с помощью трубы.

Очень часто последовательно-параллельное соединение используется в электротранспорте. Недавно я делал батарею для своего электровелосипеда из li-ion аккумуляторов 18650. Для моего электробайка требовалось напряжение в 36 Вольт. Итак, теперь включаем логику. Один аккумулятор выдает 3,6 Вольт. Чтобы получить 36 Вольт, мне надо соединить 10 аккумуляторов последовательно.

Чтобы было проще для понимания, я их нарисую не по ГОСТу:

Ура! Я получил 36 Вольт для своего электровелосипеда. Но вот проблема в том, что один такой аккумулятор может отдать в нагрузку силу тока 2800 миллиАмпер в течение 1 часа или 2,8 Ампер в течение 1 часа. Такой параметр указывается на аккумуляторах как mAh. Об этом я подробно писал в этой статье «Как измерить ток и напряжение мультиметром«.

То, что я все аккумуляторы соединил последовательно, не означает, что их емкость возросла в 10 раз. В 10 раз возросло только напряжение, так как я их соединил последовательно. То есть общая сумма получилась 36 Вольт и все те же самые 2800 mAh как и у одного аккумулятора.

Поэтому, чтобы увеличить емкость, я должен в параллель этой ветви соединить точно такую же ветвь из аккумуляторов, иначе мой электровелосипед не проедет и пару тройку километров. Я ведь хочу кататься весь день!

Сказано — сделано. Цепляем еще одну ветвь в 36 Вольт. Вы ведь не забыли правило, что при параллельном соединении у нас напряжение должно быть одинаково? В результате мы получаем что-то типа этого:

Итого, мы получили те же самые пресловутые 36 Вольт, но вот емкость увеличилась в два раза. 2800 mAh +2800 mAh = 5600 mAh. Ну вот, с такой батареей можно проехать уже чуть дальше. Но мне этого тоже показалось мало, поэтому я добавил еще 2 ветви. В результате моя самопальная батарея для электровелосипеда схематически, по идее, должна выглядеть вот так:

Пару слов о BMS (Battery Management System)

Дело в том, что для того, чтобы управлять зарядом, предохранять от короткого замыкания и управлять силой выдаваемого тока к такой батарее надо приделать плату BMS (Battery Managment System). Самые простые выглядят вот так:

Чуть получше и дороже:

10S 36V на BMS говорит нам о том, что эта BMS рассчитана для 10 аккумуляторов, включенных последовательно. Если на каждом аккумуляторе будет по 3,6 В, следовательно, 10х3,6=36 Вольт что и написано на самой BMS.

Discharge current — ток разрядки, то есть максимальный выдаваемый ток

Charge current — ток зарядки, то есть максимальный ток заряда

Внутри такой платы имеется все, чтобы полностью управлять состоянием батареи.

Схемы подключения таких BMS выглядят примерно вот так:

Как вы видите, у нас BMS вроде как должна заряжать только 10 банок в ряд. Но в нашей самопальной батарее их 40. Что же делать? Почему бы вместо одной банки не поставить в параллель 4 банки и не обмануть BMS?

Получается, схема с BMS 10s4p под плату с BMS будет выглядеть вот так:

В сообществе электронщиков и самоделкиных такая батарея называется 10S4P. Расшифровывается очень просто:

S — serial — с англ. — последовательный.

P — parallel — параллельный.

В нашем случае 10 аккумуляторов последовательно и 4 в параллель — 10S4P. Все до боли просто)

А вот выглядит моя самопальная батарея для электровелосипеда пока что без модуля BMS.

Источник