первообразные корни и индексы

Первообразные корни и индексы

Порядок числа по данному модулю

натуральное число к, такое, что:

Если целые а и Z/сравнимы по mod т, т.е.

Таким образом, все элементы класса вычетов a mod т имеют порядок к. Число к называется порядком класса вычетов а по модулю т.

Первообразный корень по модулю m

Теорема 2.64

Доказательство. Допустим противное, т.е. пусть

a s = a f (mod т) (2.305)

Так как а и т взаимно просты, то ad и т также взаимно просты.

Разделим обе части сравнения (2.305) на cd:

2 образует приведенную систему вычетов по модулю р.

Теорема 2.65

Доказательство. Произведем деление чисел п и к

n = kq + r, 0 п = 1 (mod m)

a kq+r = l(mod т) (2.313)

Но если г Ф 0, to a r 1 (mod m).

Получили противоречие, следовательно, г = 0.

Следствие 1. Пусть а Є Z, р Є N, тогда порядок числа а по модулю р является делителем kl = a k2 (mod т)

Доказательство. Докажем, что если верно сравнение

то верно и сравнение

Так как а к2 и т взаимно просты, то

но так как если к = 6(amodm) и а т = 1 (modni), то п кратно к, получаем, что разность к_г — к₂ кратно к, то есть к_г = k₂(modk’).

Обратно, пусть верно сравнение

Умножим это сравнение на а к2 :

a kl = a k2 (modm). (2.323)

эквивалентны между собой.

Источник

Первообразные корни и индексы. Порождающий элемент и дискретный логарифм.

В этом параграфе рассмотрены теоретико-числовые основы, ведущие к задачам дискретного логарифмирования над конечным полем, а также приведены некоторые приложения теории конечных групп к таким вопросам как тесты на простоту и построение простых чисел.

Основные понятия и теоремы.

При (a,m)=1 существуют положительные γ с условием a γ ≡1(mod m). Наименьшее из таких γ называется показатель, которому a принадлежит по модулю m.

В том, что такие γ существуют, можно убедиться, вспомнив теорему Эйлера (γ=φ(m)).

Докажем несколько важных теорем, описывающих свойства O_m(a):

Теорема 1.

Действительно, из того, что a l ≡a k (mod m), 0 ≤ k l — k ≡1(mod m), 0 γ ≡a β (mod m) 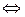γ≡β(mod δ).

Пусть теперь γ≡β(mod δ) Тогда, по теореме делимости, найдутся такие числа q, w, r: 0 ≤ r δ ≡1(mod m) следует, что

Что и требовалось доказать.

Теорема 3.

Следует из Теоремы 2 при β=0 и из теоремы Эйлера (a φ ( m ) ≡1(mod m)).

Последняя теорема также может быть доказана как следствие из теоремы Лагранжа (порядок любого элемента в группе делит порядок группы) применительно к группе U_m.

Числа, принадлежащие показателю φ(m) (если они существуют), называются первообразными корнями по модулю m.

Если существует первообразный корень по модулю m, то мультипликативная группа U_m является циклической группой.

Доказательство очевидным образом следует из вышесказанного.

2: 2 0 =1, 2 1 =2, 2 2 =4, 2 3 =8, 2 4 =5, 2 5 =10, 2 6 =9, 2 7 =7, 2 8 =3, 2 9 =6, 2 10 =1. O₁₁(2)=10.

3: 3 0 =1, 3 1 =3, 3 2 =9, 3 3 =5, 3 4 =4, 3 5 =1. O₁₁(3)=5.

4: 4 0 =1, 4 1 =4, 4 2 =5, 4 3 =9, 4 4 =3, 4 5 =1. O₁₁(4)=5.

5: 5 0 =1, 5 1 =5, 5 2 =3, 5 3 =4, 5 4 =9, 5 5 =1. O₁₁(5)=5.

6: 6 0 =1, 6 1 =6, 6 2 =3, 6 3 =7, 6 4 =9, 6 5 =10, 6 6 =5, 6 7 =8, 6 8 =4, 6 9 =2, 6 10 =1. O₁₁(6)=10.

7: 7 0 =1, 7 1 =7, 7 2 =5, 7 3 =2, 7 4 =3, 7 5 =10, 7 6 =4, 7 7 =6, 7 8 =9, 7 9 =8, 7 10 =1. O₁₁(7)=10.

8: 8 0 =1, 8 1 =8, 8 2 =9, 8 3 =6, 8 4 =4, 8 5 =10, 8 6 =3, 8 7 =2, 8 8 =5, 8 9 =7, 8 10 =1. O₁₁(8)=10.

9: 9 0 =1, 9 1 =9, 9 2 =4, 9 3 =3, 9 4 =5, 9 5 =1. O₁₁(9)=5.

10: 10 0 =1, 10 1 =10, 10 2 =1. O₁₁(10)=2.

Действительно, порядки всех элементов делят порядок группы. При этом в группе U₁₁ нашлись порождающие элементы, причем не один, а четыре. Это 2, 6, 7 и 8. Однако не во всех группах U_m существуют порождающие элементы, убедимся в этом на следующем примере:

3: 3 0 =1, 3 1 =3, 3 2 =1. O₈(3)=2.

5: 5 0 =1, 5 1 =5, 5 2 =1. O₈(5)=2.

7: 7 0 =1, 7 1 =7, 7 2 =1. O₈(7)=2.

Итак, в группе U₈ нет порождающего элемента.

Возникает вопрос – в каких группах U_m порождающий элемент существует, а в каких – нет, и как найти порождающий элемент? На этот вопрос ответим в следующих пунктах данного параграфа.

6.2. Существование первообразных корней по модулю p.

Лемма 1.

O_m(x)=ab O_m(x a )=b.

Лемма 2.

O_m(x)=a, O_m(y)=b, (a,b)=1 O_m(xy)=ab.

Доказательства этих лемм не представляют принципиальной сложности, поэтому предоставляются читателю в качестве упражнения.

Теорема 1 (Критерий Люка).

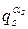
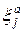
Тогда, согласно Лемме 1, O_p(η)= , где η= .

Согласно Лемме 2, O_p(g)=τ= 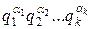, где g=η₁η₂…η_k.

Поэтому, согласно Теореме 3, п.1, τ\(p—1).

Теорема (о существовании первообразного корня по модулю p α )

Пусть g – первообразный корень по модулю p, тогда существуют такое число t, что u= не делится на p, и тогда g+pt – первообразный корень по модулю p α α>1.

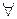
Число u, заданное условием, является целым в силу теоремы Ферма. Действительно, поскольку g U_p, то (g,p)=1 (g+pt,p)=1 по теореме Ферма, (g+pt) p —1 ≡1(mod p) p\((g+pt) p —1 –1).

где если t пробегает Z_p, то и u пробегает Z_p (полную систему вычетов по модулю р). Поэтому существует такое t Z_p, для которого u не делится на p. При таком t из (*) получаем:

Теорема 2.

Доказанные теоремы вкупе с теоремой о существовании первообразных корней по модулю p позволяют сделать следующий

p=71, наименьший первообразный корень по модулю 71 есть 7.

Найти первообразный корень по модулю 71 α и 2·71 α для всех α.

Согласно Теореме 1, нужно найти такое t, чтобы (g+pt) p — 1 —1 0(modp 2 ).

Будем перебирать t:

7 70 —1 mod 5041 = (7 10 ) 7 –1 mod 5041 = 2814 7 —1 mod 5041 =

= (2814 2 ) 3 ·2814—1 mod 5041 = 4226 2 ·4226·2814—1 mod 5041=

= 3854·4226·2814 –1 mod 5041 = 1562 ≠ 0.

Итак, 7 – первообразный корень по модулю 71 α для всех α.

Вообще говоря, нам повезло, первое же испытанное число t подошло. В другом случае, возможно, пришлось бы перебирать несколько t, прежде чем отыскали бы первообразный корень.

Разумеется, мы не отыскали все первообразные корни по данному модулю. Алгоритмы нахождения их весьма трудоемки, особенно тогда, когда требуется найти все или несколько первообразных корней.

Дата добавления: 2015-11-28 ; просмотров: 1845 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Глава 6 первообразные корни и индексы

1 Общие теоремы

При (a, m) = 1 существуют положительные γ с условием α γ ≡ 1(mod т), например (теорема Эйлера) γ = φ(m). Наименьшее из них называется: показатель, которому а принадлежит по модулю т.

Доказательство: Из α l ≡ α k (mod т), 0 ≤ k l — k ≡ 1(mod т); 0 γ ≡ α γ ′(mod т) тогда и только тогда, когда γ = γ′(mod δ); в частности (при γ′ = 0), a γ ≡ 1(mod m) тогда и только тогда, когда γ делится на δ.

,

.

Поэтому α γ ≡ α γ ′(mod т) тогда и только тогда, когда , т. е. Из Теоремы 1, когда r = r₁.

Пусть а по модулю m принадлежит показателю δ. Тогда из Теоремы 2 (γ′ = 0) и из a φ ( m ) ≡ 1(mod m) следует, что φ(m) делится на δ. Таким образом, показатели, которым числа принадлежат по модулю т, суть делители φ(m). Наибольший из этих делителей есть само φ(m). Числа, принадлежащие показателю φ(m) (если такие существуют), называются первообразными корнями по модулю т.

2 Первообразные корни по модулям pα и 2рα

Если x по модулю m принадлежит показателю ab, то x a принадлежит показателю b.

Доказательство: Пусть x a принадлежит показателю δ. Тогда (x a ) δ ≡ 1(mod m), откуда x aδ ≡ 1(mod m); следовательно (Теорема 2, п. 1), aδ делится на ab, т. е. δ делится на b. С другой стороны, x ab ≡ 1(mod m), откуда (x a ) b ≡ 1(mod m); следовательно (Теорема, 2 п. 1), bделится на δ. Поэтому δ = b.

Если x по модулю m принадлежит показателю a, а y — показателю b, причем (a, b) = 1, то xy принадлежит показателю ab.

Доказательство: Пусть xy принадлежит показателю δ. Тогда (xy) δ ≡ 1(mod m). Отсюда x bδ y bδ ≡ 1(mod m) и (Теорема 2, п. 1) x bδ = 1 (mod m). Поэтому (Теорема 2, п. 1) bδ делится на a, и ввиду (b, a) = 1δ делится на a. Так же находим, что δ делится на b. Делясь же на a и на b, ввиду (a, b) = 1δ делится и на ab. С другой стороны, из (xy) ab ≡ 1(mod m) следует (Теорема 2, п. 1), что ab делится на δ. Поэтому δ = ab.

Существуют первообразные корни по модулю p.

где, одновременно с t, u пробегает полную систему вычетов по модулю р. Поэтому можно указать t с условием, что и не делится на р. При таком t из (2) выводим

,

,

,

Источник