перемычка в магнитном поле

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Перемычка между шинами в магнитном поле-короткое замыкание?

Последний раз редактировалось artempalkin 27.09.2020, 11:48, всего редактировалось 4 раз(а).

Загадочная задача. Точнее, сначала вроде все понятно, а потом резко становится непонятно.

Хорошо, вроде бы все несложно. Составляем второй закон Ньютона для перемычки и закон Ома для всей цепи, учитывая магнитные явления:

Ну и как бы получается система диф. уравнений. Находим отсюда уравнение на , оно в любом случае получится линейным, решаем его, подставляем начальные условия, можно даже исследовать решение, короче говоря, небезынтересная и простая задача.

Надо сказать, что там много вариантов есть с разными условиями. Так вот тут я смотрю, а мои условия: , (. ). Тут я в полном непонимании, задача становится абсолютно непонятной.

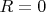
Получается, цепь накоротко замкнута с катушкой. Я поискал, что это может значить, везде упоминается какое-то внутреннее сопротивление катушки, которое должно быть в таком случае, но тут-то ничего такого нет. Обидно то, что в остальных вариантах адекватные условия, которые make sense, а тут я не понимаю физики сути задачи. Подскажите, о чем вообще речь, как подступиться?

Я тут, после того, как напечатал уже, подумал: так может на самом деле просто ЭДС индукции контура равна ЭДС самоиндукции катушки? Так и получится, если формально подставить нулевое сопротивление. Тогда уравнения даже проще решаются. Но при этом я не очень понимаю физику процесса.

Но тогда получается, что ЭДС в контуре равна нулю, сопротивления нет, но при этом ток все равно течет. я что-то в недоумении.

Заслуженный участник

Последний раз редактировалось Prisma 27.09.2020, 12:01, всего редактировалось 1 раз.

Последний раз редактировалось artempalkin 27.09.2020, 12:19, всего редактировалось 4 раз(а).

Вы подразумеваете, что решить в общем виде (с ненулевым ), а потом устремить к нулю?

Я подозреваю, что в таком случае получится то же самое, как если сразу приравнять к нулю

Последний раз редактировалось Prisma 27.09.2020, 12:32, всего редактировалось 1 раз.

Последний раз редактировалось artempalkin 27.09.2020, 12:43, всего редактировалось 1 раз.

Да, решения не будут отличаться, если сразу подставить 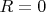или потом устремить к нулю (это очевидно из свойств корней многочлена (характеристического в нашем случае)). И решение получается небессмысленное (перемычка будет колебаться вокруг некоторого положения).

Да, спасибо, пример очень хороший. По поводу сверхпроводимости понятно. Наша ситуация какая-то другая. При отсутствии сопротивления ток в цепи по идее должен нарастать к бесконечности. При этом катушке это не нравится, и она начинает мешать току нарастать, создавая встречную ЭДС. Но эта ЭДС не полностью убивает ток (тогда бы перемычка свободно падала, ток в цепи не течет, ну, некоторый смысл я вижу), не делает его постоянным (тогда возникла бы ситуация по типу сверхпроводимости, которую вы описали, но это тоже не наш случай: у нас ток тоже меняется гармонически вокруг некоторого значения).

Последний раз редактировалось artempalkin 27.09.2020, 16:35, всего редактировалось 2 раз(а).

Последний раз редактировалось fightingphysics 27.09.2020, 17:50, всего редактировалось 3 раз(а).

Тут похоже на замыкание головного мозга автора задачи. Разумеется любое шунтирование нагрузки является кз, если мы пренебрегаем сопротивлением самого шунта и участка от источника. Причем тут магнитное поле, вообще непонятно, при шунтировании оно все равно исчезнет

Работал я как то в отделе энергетика, и пришел малый, после тех вуза, инженер, специалист конкретно по должности. Видать тоже 5 лет его парили такими вот «задачами», красный диплом и мамка физику преподавала в школе, а итог тупей простого электрика. Запарился насчет банального последовательного подключения, он думал что ток 2 последовательных лампочек растет а не падает. Хотя это и безо всяких ньютонов очевидно, энергии меньше потребляется, значит и ток меньше. До него даже это не допирало почему то

Ему вроде типа «интуитивно» казалось, что чем мы больше нагрузки в цепь накидываем, тем больше ток, хотя при постоянном источнике справедливо обратное, и это вроде как тоже вполне интуитивно, как если бы мы из бутылки водку в стаканы разливали, чем больше стопариков, тем меньше в каждом из них водяры, и тем меньше каждый инженер-потребитель водяры нажрется:)

То есть думаете, что в реальной жизни (даже если как-то круто подобрать параметры, чтобы макроскопически, так сказать, колебания перемычки возможно было наблюдать) такая ситуация невозможна?

Не знаю что тут сказать, сейчас система такая, что кругом какие то-чудеса ищут, физика стала сказкой, детей сейчас в школе учат что 2 закон термодинамики доказывает боженьку-криэйтора:)
Да и не сейчас это, а давным давно. Ньютон он ведь и сам христианский проповедник был, а не натурфилософ. У него там модели мама не горюй, дескать свет это камни которые летят через пустоту, прямо как у древнегреческих атомистов седых веков до нашей эры

Источник

§ 5.9. Примеры решения задач

При решении задач на материал этой главы нужно уметь с помощью правила Ленца определять направление индукционного тока. Для вычисления ЭДС индукции следует использовать формулы (5.3.3), (5.5.2), а для ЭДС самоиндукции и взаимной индукции — формулы (5.7.2) и (5.7.4). Энергию тока вычисляют по формуле (5.8.1), а плотность энергии магнитного поля — по формуле (5.8.6). Для решения некоторых задач надо применять закон Ампера (4.7.9).

Задача 1

Проволочное кольцо радиусом г находится в однородном магнитном поле, индукция которого перпендикулярна плоскости кольца и меняется с течением времени по закону В = kt. Определите напряженность электрического поля в витке.

Решение. Согласно закону электромагнитной индукции (5.3.2)

с другой стороны, ЭДС индукции численно равна работе, совершаемой вихревым электрическим полем при перемещении единичного положительного заряда вдоль проволочного кольца (см. § 4.4), т. е.

Сравнивая выражения (5.9.1) и (5.9.2), получим:

Задача 2

В однородном проволочном кольце создан постоянный индукционный ток I. Линии индукции переменного магнитного поля, создающего этот ток, перпендикулярны плоскости кольца. Поле сосредоточено вблизи его оси и имеет ось симметрии, проходящую через центр кольца (рис. 5.18). Чему равна разность потенциалов между точками А и В? Что будет показывать электрометр, присоединенный к этим точкам?

Решение. Разность потенциалов между любыми точками кольца должна быть равна нулю. В противном случае мы придем к противоречию, применяя закон Ома к короткому и длинному участкам кольца. Кроме того, это очевидно и из соображений симметрии.

Отсутствие разности потенциалов означает, что кулонов-ское поле внутри кольца равно нулю. Ток возникает вследствие наличия ЭДС индукции, распределенной равномерно вдоль кольца:

где е_i, и E_i — ЭДС индукции на коротком и длинном участках кольца, а r и R — соответственно сопротивления участков.

Несмотря на отсутствие разности потенциалов между точками А к В, электрометр обнаружит разность потенциалов между стержнем и корпусом.

Дело в том, что в проводниках АС и BD ток равен нулю. Следовательно, в каждой точке этих проводников стороннее электрическое поле индукционного происхождения уравновешивается кулоновским (потенциальным) полем, возникающим вследствие перераспределения зарядов в проводниках под влиянием ЭДС индукции. Работа потенциальных сил при перемещении по замкнутому контуру ACDBA равна нулю. На участке АВ кулоновское поле отсутствует. При перемещении единичного заряда по проводникам АС и BD работа потенциальных сил численно равна ЭДС индукции в этих проводниках и имеет противоположный знак.

Следовательно, для равенства нулю работы кулоновских сил вдоль замкнутого контура необходимо, чтобы разность потенциалов между точками С к D равнялась ЭДС индукции в проводниках АС и DB и совпадала с ней по знаку. Так как ЭДС индукции в замкнутом контуре ACDBA равна нулю (магнитное поле не пронизывает этот контур), то на участке АВ ЭДС индукции равна по модулю и противоположна по знаку ЭДС в проводниках АС и ВD, если пренебречь работой сторонних сил индукции на участке между стержнем и корпусом электрометра по сравнению с работой в проводниках АС и BD.

Поэтому электрометр покажет разность потенциалов, приблизительно равную ЭДС на участке АВ.

Задача 3

По параллельным рельсам, наклоненным под углом α = 30° к горизонту, соскальзывает без трения с постоянной скоростью υ = 1 м/с проводящая перемычка массой m — 100 г. В своей верхней части рельсы замкнуты проводником. Рельсы с перемычкой нгдодятся в однородном магнитном поле, индукция которого направлена вертикально. Сопротивление перемычки R = 2 Ом гораздо больше сопротивления остальной части системы. Чему равна сила тока I в перемычке?

Решение. На перемычку действуют три силы: сила тяжести m, сила реакции рельсов и сила Ампера _A, направленная вправо (рис. 5.19). Направление силы Ампера не зависит от направления вектора В. При изменении направления В на противоположное меняется направление индукционного тока, возникающего в перемычке при ее движении, но направление силы Ампера не меняется.

Так как, согласно условию, перемычка соскальзывает по рельсам с постоянной скоростью без трения, то векторная сумма действующих на нее сил равна нулю:

Запишем это уравнение для модулей проекций на ось X, направленную так, как показано на рисунке 5.19:

Сила Ампера, действующая со стороны магнитного поля на перемычку, равна:

где В — индукция магнитного поля, l — длина перемычки. Тогда уравнение (5.9.3) примет вид:

ЭДС индукции, возникающая в перемычке при ее движении вниз по рельсам со скоростью , равна:

Согласно закону Ома

Поделив почленно равенство (5.9.4) на равенство (5.9.5), получим:

Задача 4

Из провода длиной l изготовили соленоид длиной l₀. Диаметр соленоида d 2 B₀, а индукционный ток меняется при этом от 0 до I, получим:

Упражнение 9

1. Катушка из ω витков, площадь каждого из которых равна S, присоединена к баллистическому гальванометру. (Баллистический гальванометр измеряет прошедший через него заряд.) Сопротивление всей цепи R. Вначале катушка находилась между полюсами магнита в области, где магнитная индукция постоянна по модулю и направлена перпендикулярно виткам катушки. Затем катушку переместили в пространство, где магнитное поле отсутствует. Чему равен заряд q, прошедший через гальванометр?

2. Прямоугольная рамка ABCD расположена в плоскости бесконечного прямолинейного проводника с током, причем стороны AD и ВС параллельны проводнику (рис. 5.20). В середине стороны DC включен прибор, измеряющий заряд, протекающий по контуру (на рисунке не показан). Рамку можно перевести в новое положение, изображенное на рисунке 5.20 ихтриховой линией, двумя способами: а) перемещая ее параллельно самой себе; б) вращая на 180° вокруг стороны ВС. В каком случае заряд, протекший через прибор, больше?

3. Прямоугольный контур ABCD перемещается поступательно в магнитном поле тока I, текущего по длинному прямому проводу 00′ (рис. 5.21). Стороны AD и ВС параллельны проводу. Определите силу тока, индуцированного в контуре, если контур перемещается с постоянной скоростью и; AD = ВС = a; АВ = DC = b. Сопротивление контура R.

5. Определите силу тока в проводниках цепи, изображенной на рисунке 5.22, если индукция однородного магнитного поля перпендикулярна плоскости чертежа и модуль ее изменяется по закону В = kt. Сопротивление единицы длины проводников равно r.

6. Переменное магнитное поле создает в кольцевом проводнике ADBKA постоянную ЭДС индукции E. Сопротивления проводников ADB, АКВ и АСВ (рис. 5.23) равны соответственно R₁, R₂ и R₃. Какую силу тока показывает амперметр, включенный в участок АСВ? Магнитное поле сосредоточено у оси кольцевого проводника.

7. Прямоугольная проволочная рамка со сторонами а = 5 см и b = 10 см входит с постоянной скоростью υ = 1 м/с своей меньшей стороной в большую область однородного магнитного поля, индукция которого, равная по модулю В = 0,01 Тл, направлена по нормали к плоскости рамки. Сопротивление рамки R = 0,01 Ом. Какую работу А совершает индукционный ток за время Δt = 0,5 с с момента, когда рамка начинает входить в поле?

8. По двум вертикальным рейкам АВ и CD (рис. 5.24), соединенным резистором R, может без трения скользить проводник длиной l и массой m. Система находится в однородном магнитном поле, индукция которого перпендикулярна плоскости рисунка и направлена к нам. Как будет двигаться подвижный проводник, если пренебречь сопротивлением самого проводника и реек?

9. Проводник длиной l может без трения скользить по рейкам АВ и CD, соединенным через резистор сопротивлением R (рис. 5.25), в однородном магнитном поле, индукция которого перпендикулярна плоскости чертежа. Какую силу следует приложить к проводнику, чтобы он двигался равномерно со скоростью ?

11. По двум металлическим параллельным рейкам, расположенным в горизонтальной плоскости и замкнутым нa конденсатор С, может без трения двигаться проводник массой m и длиной l. Вся система находится в однородном магнитном поле, индукция которого направлена вверх. К середине проводника перпендикулярно к нему и параллельно рейкам приложена сила (рис. 5.26). Определите ускорение подвижного проводника, если сопротивление реек, подводящих проводов и подвижного проводника равно нулю. Какие виды энергии возникают за счет работы силы ? Считать, что в начальный момент скорость проводника равна нулю. Индуктивностью цепи пренебречь.

12. На цилиндр из немагнитного материала намотан соленоид из ω витков проволоки. Радиус цилиндра r, его длина l (г > г. Центры колец лежат на прямой ОО’, перпендикулярной плоскостям обоих колец. Кольца могут перемещаться только вдоль этой прямой. В начальный момент по кольцам текут в одном направлении токи I₀ (рис. 5.28). Чему будут равны силы токов в кольцах после того, как они сблизятся вплотную?

Источник

Общий метод решения задач из разных разделов

Любой учитель, долгое время работающий в профильном классе, в конце концов приходит к двум выводам:

• невозможно разобрать на уроках все интересные задачи из методической копилки учителя, тем более что их всё больше и больше. Значит, нужно осваивать на примере ключевых задач общие методы и приёмы решения, обучая ребят не количеством, а качеством подобранных задач;

Статья подготовлена при поддержке компании «Maxceiling». Если Вы решили приобрести качественные и надежные натяжные потолки, то оптимальным решением станет обратиться в компанию «Maxceiling». Перейдя по ссылке: «натяжные потолки Балашиха», вы сможете, не отходя от экрана монитора, оставить заявку на установку натяжных потолков. Более подробную информацию о ценах и акциях действующих на данный момент вы сможете найти на сайте www.Maxceiling.Ru.

• ребёнок не может долго помнить приём решения, если его не повторять время от времени. И вот тут оказывается очень продуктивным подбирать задачи, имеющие тот же алгоритм, или приём решения, что и в предыдущей теме, даже если темы не связаны. Тогда ученика не пугает бесконечное количество задач.

Необходимо отметить, что если предлагаемый метод не будет закреплён в следующих темах, то, как бы хорошо он ни был усвоен, большинство учащихся его забывает. Неоднократное возвращение к знакомому методу происходит иногда очень неожиданно. Приводим пример решения известной задачи в теме «Механика» и использование этого алгоритма в других, казалось бы, не связанных темах.

Тема «Механика»

• Из резинового жгута длиной L и массой m изготовлено кольцо. Это кольцо вращается с угловой скоростью ω в горизонтальной плоскости вокруг вертикальной оси, проходящей через его центр. Определите силу натяжения, возникающую в кольце.

Метод решения этой задачи специфичен потому, что каждый элемент жгута при вращении имеет своё направление центростремительного ускорения, а значит, сила, действующая на каждый элемент, меняет своё направление от элемента к элементу. К тому же ученики помнят, что закон Гука применяется при упругих растяжениях прямолинейного стержня. Поэтому метод заключается в разбиении кольца на бесконечное количество малых элементов, которые практически прямолинейны в силу малости их размеров, и применении второго закона Ньютона отдельно для каждого элемента:

• Кольцо массой m изготовлено из проволоки, которая обрывается при силе натяжения Т₀. Кольцо помещают на идеально гладкий конус. При каком минимальном плоском угле конуса φ кольцо не разорвётся?

При решении этой задачи необходимо рассмотреть условие покоя малого элемента на гладкой наклонной плоскости, но алгоритм решения аналогичен.

Рассмотрим условие покоя малого элемента кольца:

N_i + m_ig + T_{упр.рез} = 0.

Силу результирующего натяжения T_{упр.рез} находим, как в предыдущей задаче:

• Жёсткость резинового жгута длиной L и массой m равна k. Кольцо, изготовленное из жгута, вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через центр кольца. Оцените, при какой угловой скорости вращения кольца ω радиус его будет равен R.

Решение аналогично предыдущей, однако требуется вспомнить закон Гука

Тема «Электростатика»

• Тонкое проволочное кольцо радиусом R несёт электрический заряд q. В центре кольца расположен одноимённый с q заряд Q, причём Q ≫ q. Определите силу Т, растягивающую кольцо.

Решение. Условие равновесия элемента кольца:

Тема «Электромагнетизм»

• Тонкое металлическое кольцо радиусом R помещается в однородное магнитное поле индукцией В так, что плоскость кольца перпендикулярна линиям магнитного поля. Определите силу упругости Т, возникающую внутри кольца при пропускании по нему тока силой I.

Тема «Механические колебания»

• Тонкое кольцо радиуса R совершает осесимметричные колебания. Определите период колебаний Т кольца. Кольцо изготовлено из материала плотностью ρ, имеющего модуль упругости Е.

Таких «перекрёстных» задач, решать которые можно одним и тем же методом, можно найти немало, и это помогает учителю. В статье использовались тексты задач, предложенных на конкурсных испытаниях при поступлении в МГТУ им. Н.Э.Баумана и МФТИ.

Источник