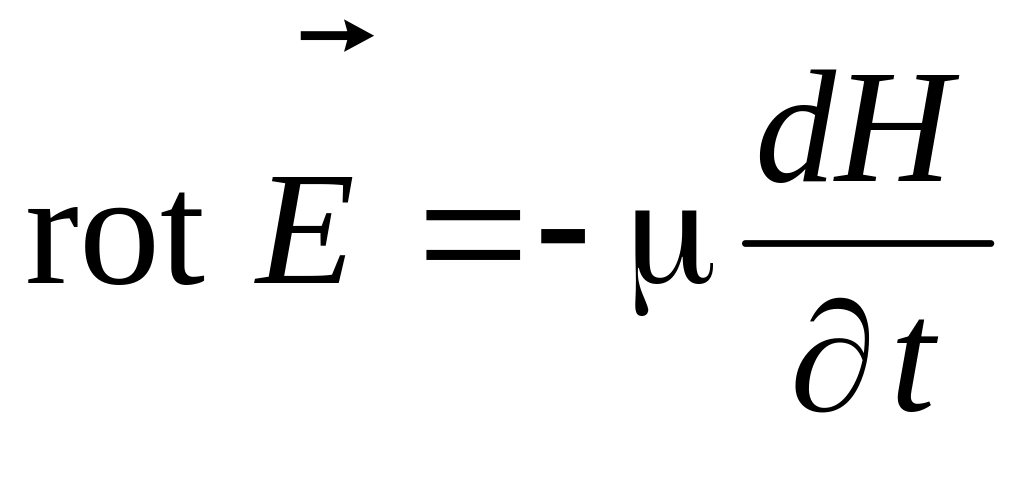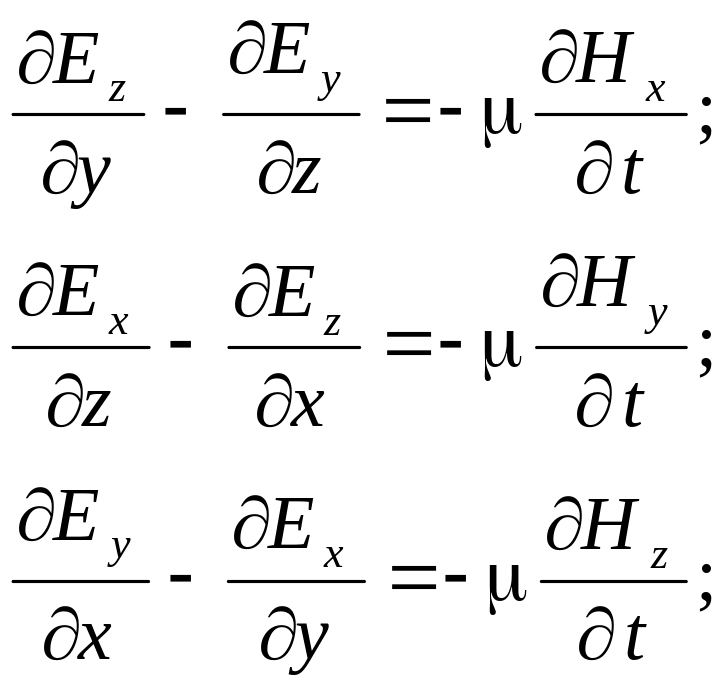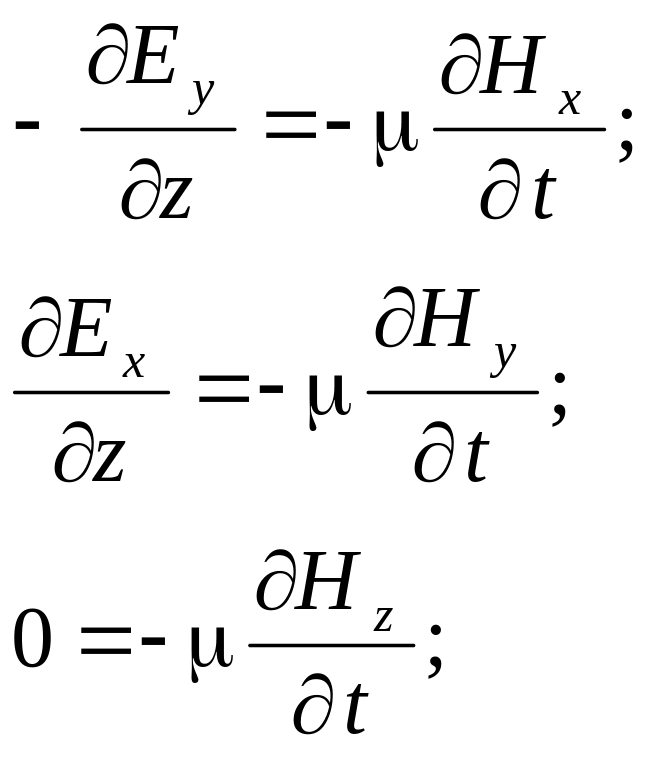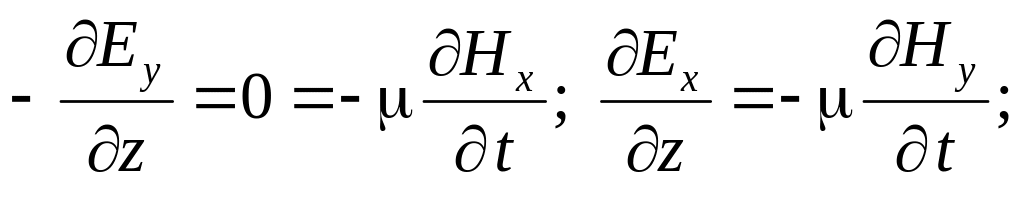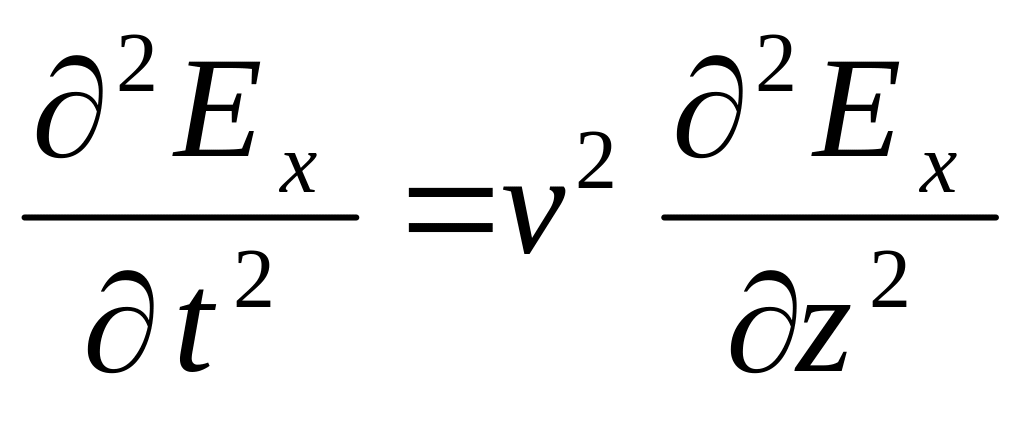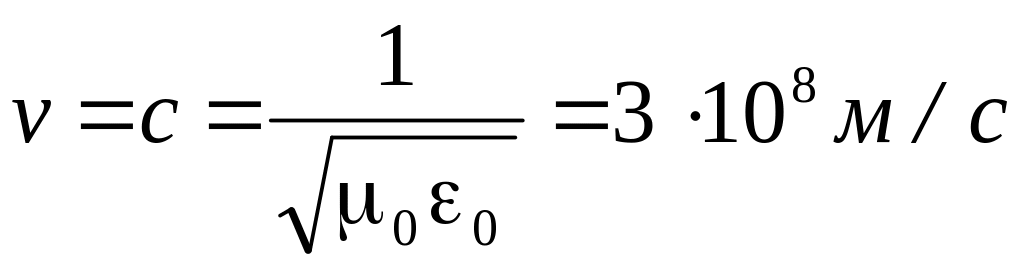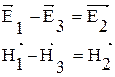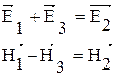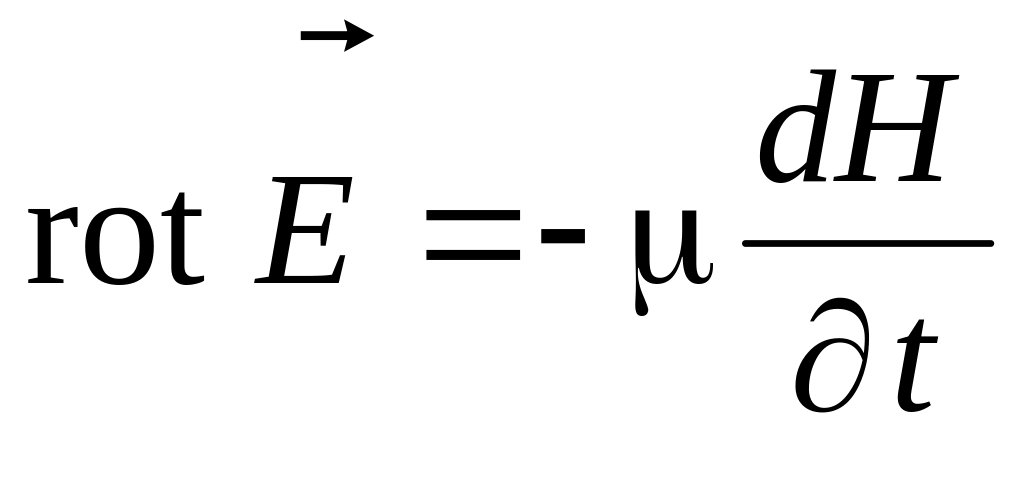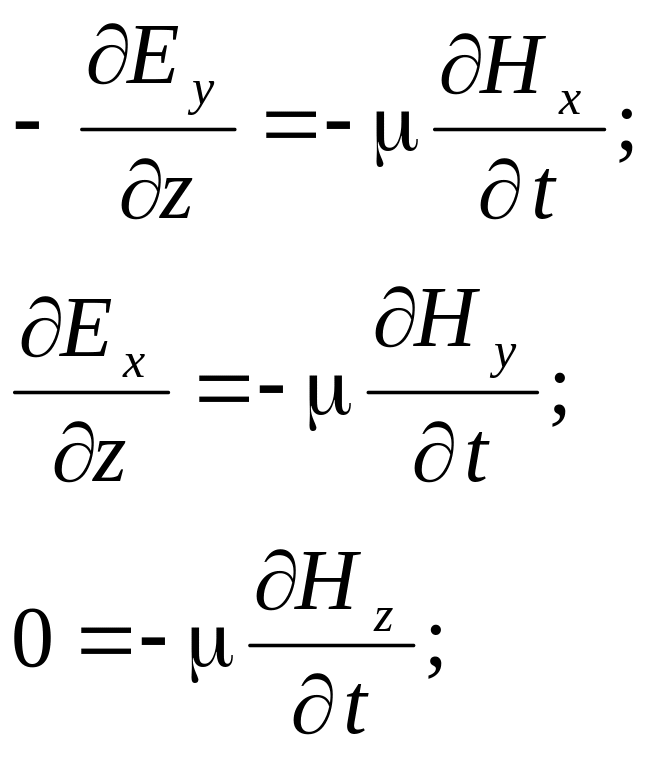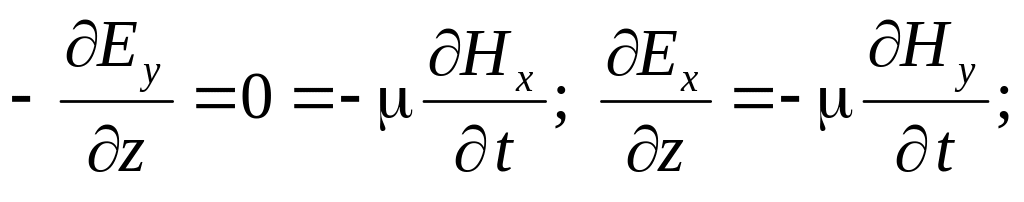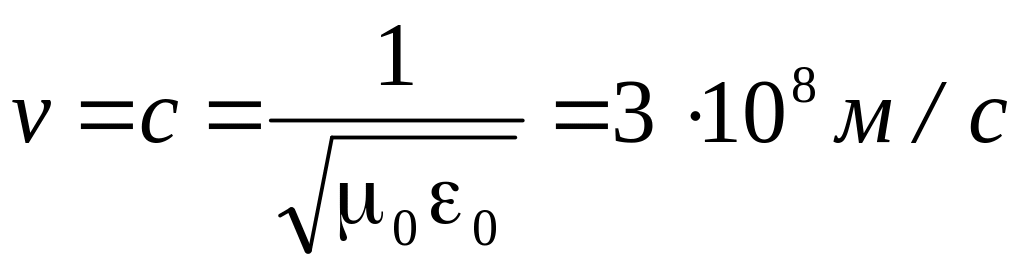переменное электромагнитное поле в диэлектрике
5 Лекция 11 Переменное электромагнитное поле в диэлектрике
В переменном электромагнитном поле наблюдаются одновременно обе, рассмотренные ранее нами в отдельности, его стороны. Связь между ними дают первое и второе уравнения Максвелла – закон полного тока и закон электромагнитной индукции:
, 
.
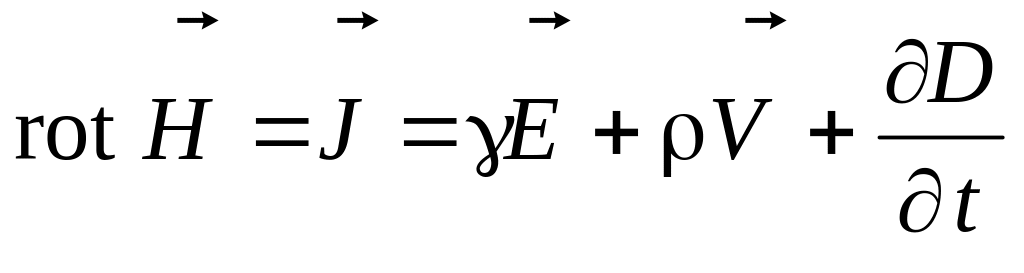
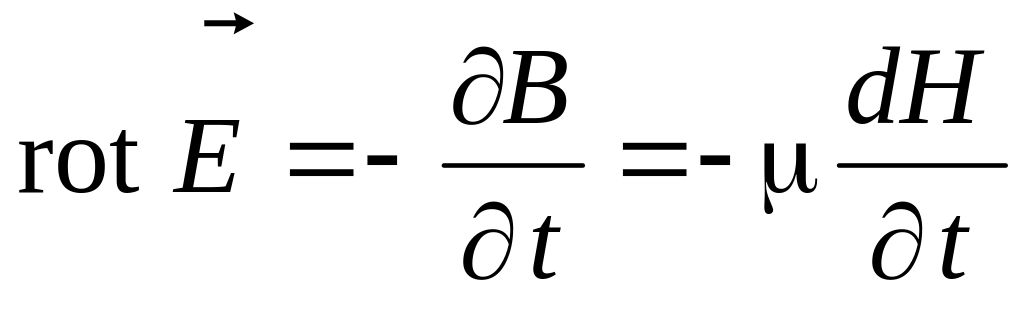
Анализируя переменное электромагнитное поле в диэлектрике, считаем диэлектрик идеальным (=0) и предполагаем отсутствие в нем объемных зарядов (=0). Тогда:
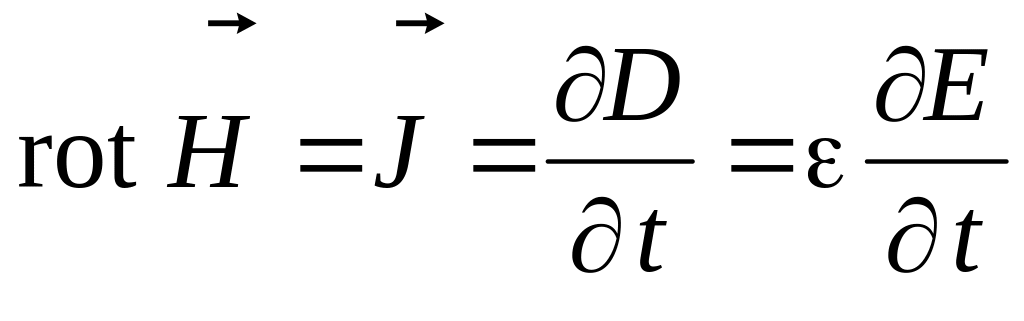
Запишем оба уравнения в проекциях на оси декартовой системы координат:
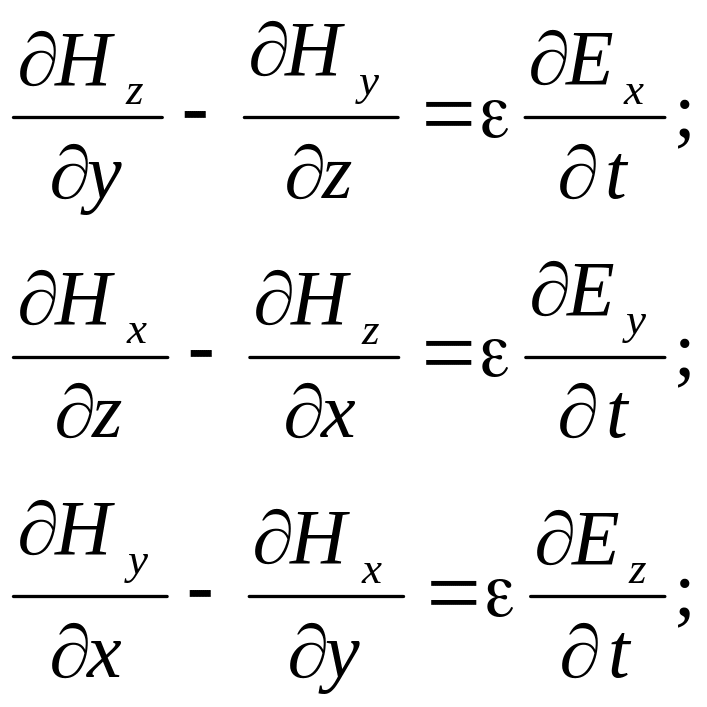
В плоской электромагнитной волне производные от любых проекций векторов поля по координатам x и y равны нулю, поэтому система уравнений упрощается и принимает вид:
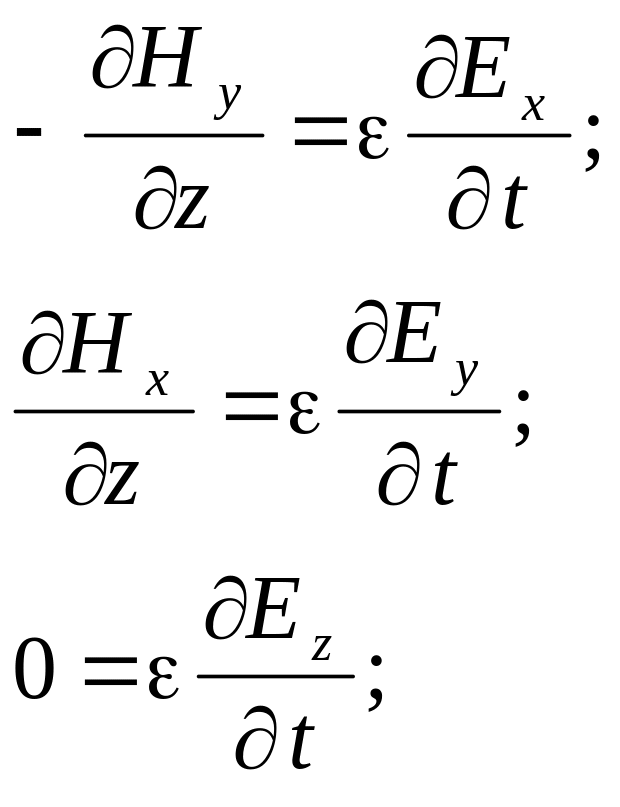
Из последних уравнений каждой системы ввиду равенства нулю производных получаем, что проекции векторов Ez и Hz не зависят от времени: Ez=const и Hz=const. Принимаем их равными нулю, так как переменное поле, излученное антенной, не содержит постоянных составляющих. Кроме того, мы уже рассматривали ранее постоянные электрические и магнитные поля, и в случае необходимости можем, если потребуется учесть их вместе с переменным полем, применив принцип наложения.
Рассматривая оставшиеся четыре уравнения для проекций, направим ось x декартовой системы координат вдоль вектора напряженности электрического поля (Ey=0). В этом случае остается единственная составляющая вектора напряженности электрического поля: E=Ex. В этом случае уравнения еще больше упрощаются:
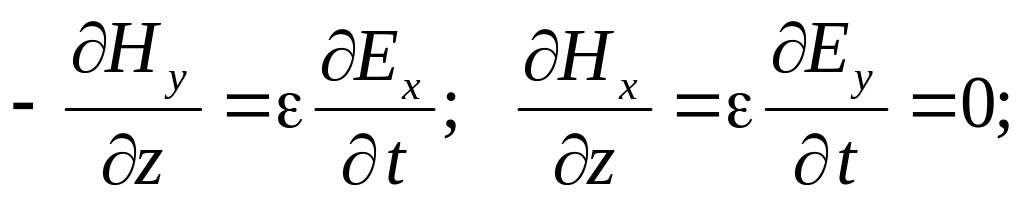
Из полученных уравнений следует, что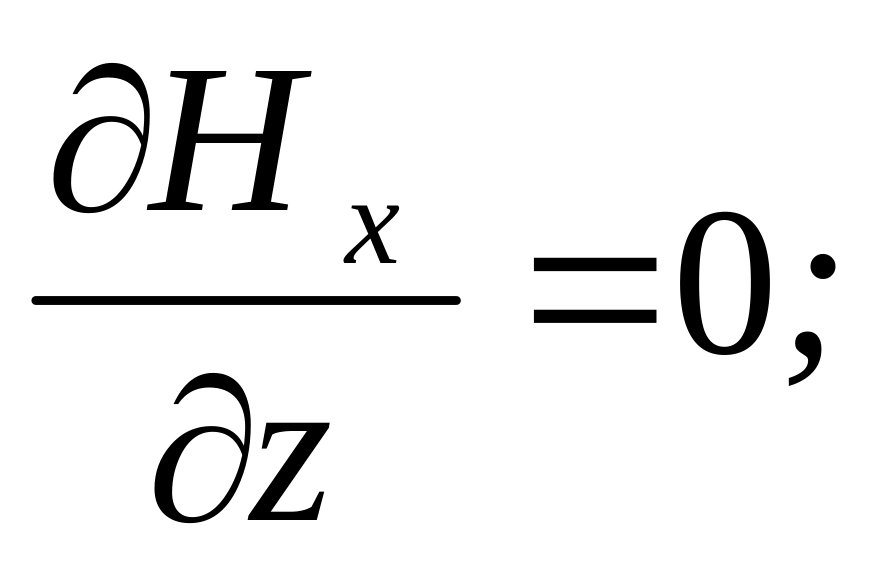 
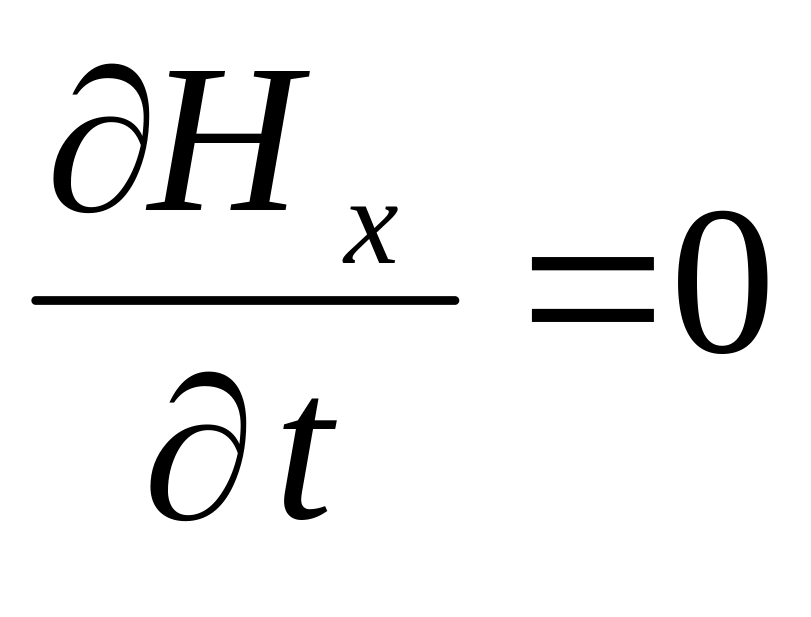
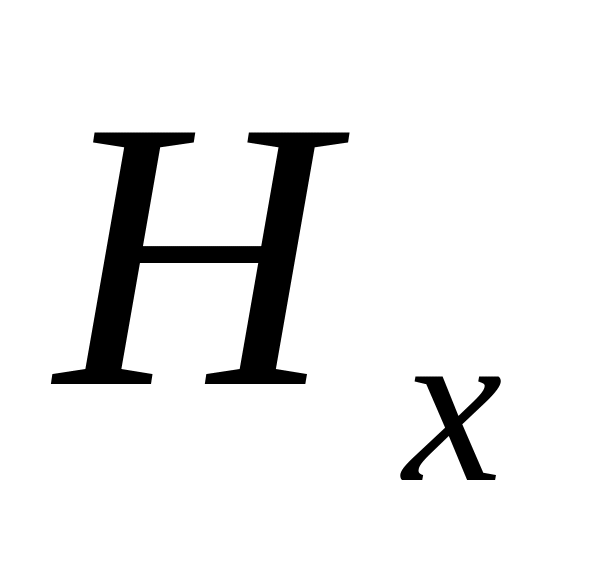
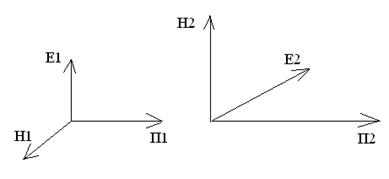
, т.е. 
=const=0,
и при выбранном направлении осей координат, вектор напряженности магнитного поля имеет лишь единственную составляющую, направленную вдоль оси y: H=Hy. Это означает, что в плоско поляризованной электромагнитной волне в диэлектрике в любой точке векторы напряженности электрического и магнитного поля расположены взаимно перпендикулярно.
Н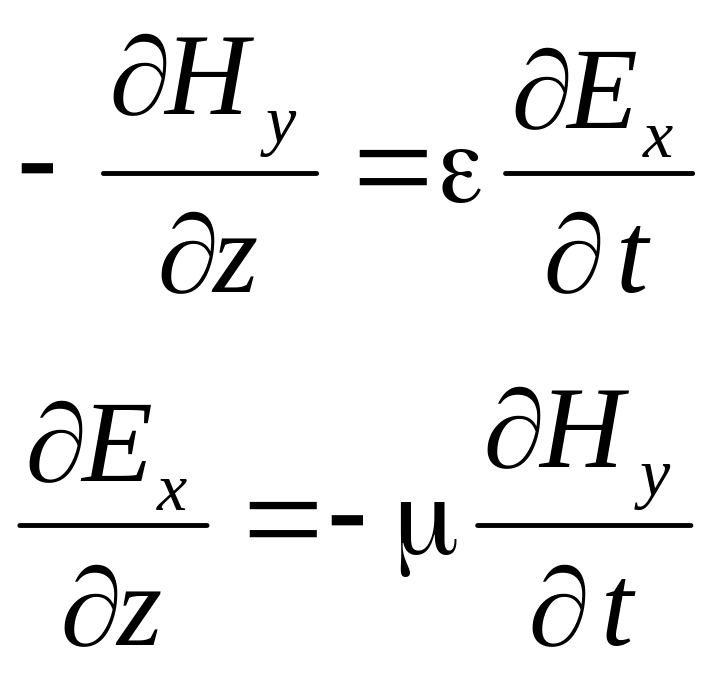 
айдем решение системы двух оставшихся уравнений:
Дифференцируя первое уравнение по времени, а второе по координате z, получим:
; 
, откуда: 
, и обозначив 
, запишем уравнение для вектора напряженности электрического поля, которое называется волновым уравнением:
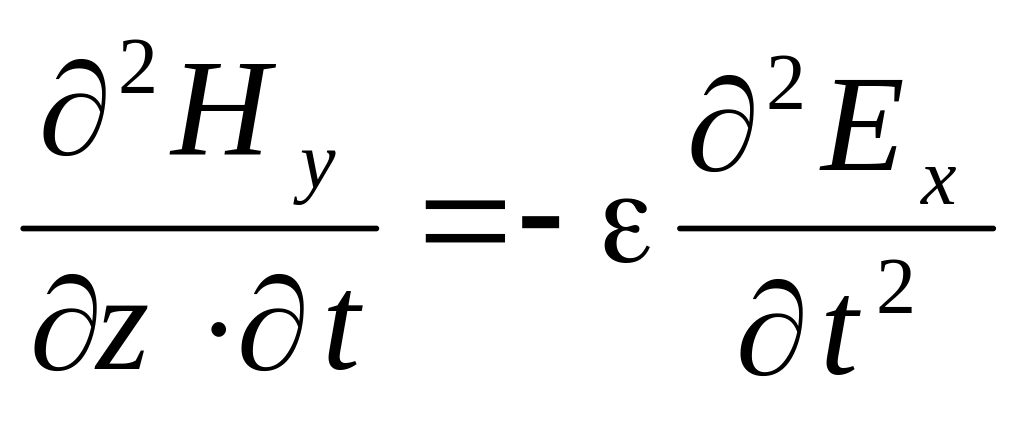
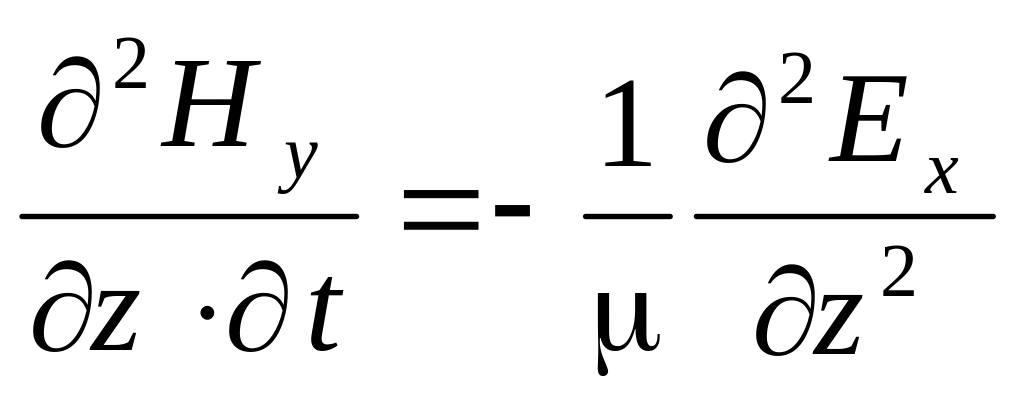
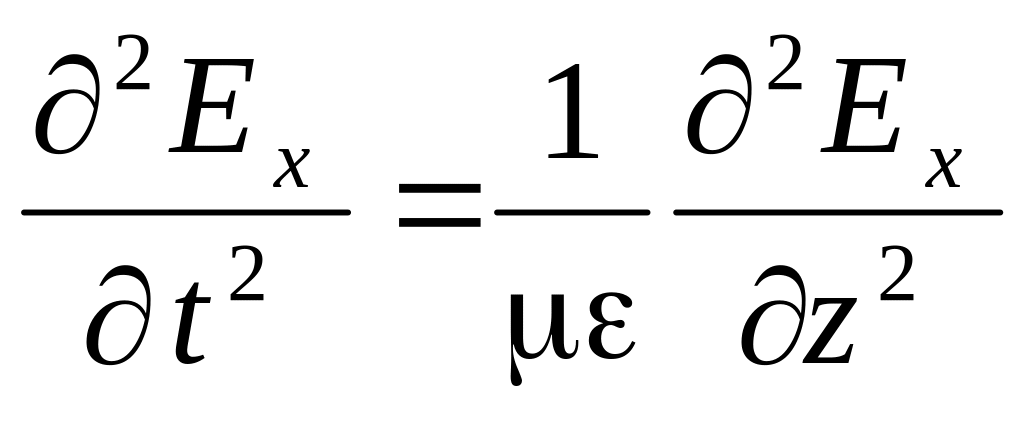
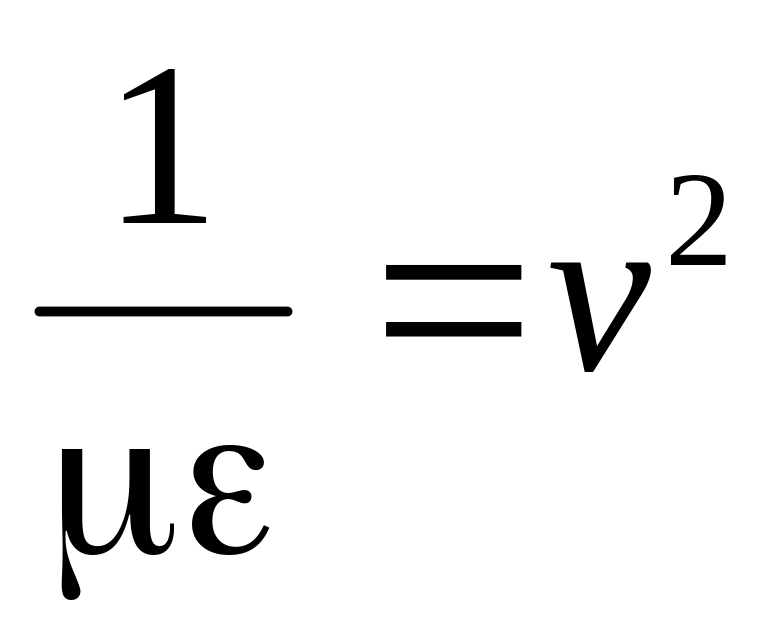
При рассмотрении режимов в цепях с распределенными параметрами нами были получены аналогичные уравнения для напряжения в произвольной точке линии без потерь, в которой координата x отсчитывается от начала линии:
.
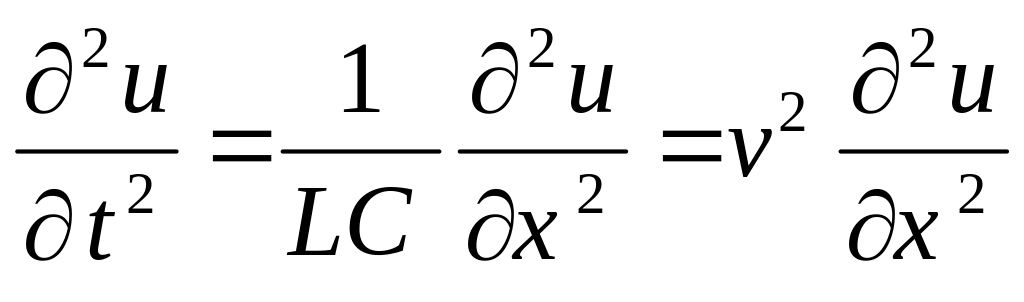
Решение для волнового уравнения в линии мы получили в виде суммы прямой и обратной бегущих волн напряжения:
Решение для напряженности электрического поля запишем по аналогии:
Коэффициенты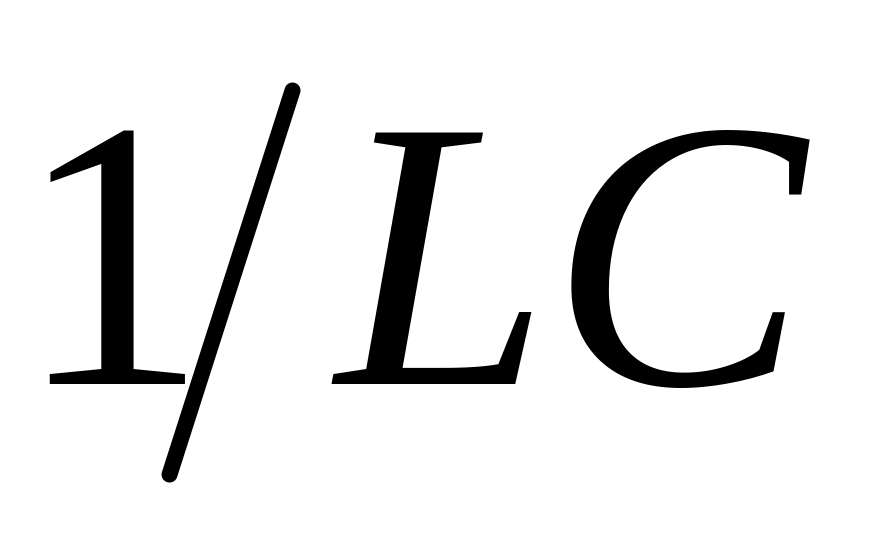 
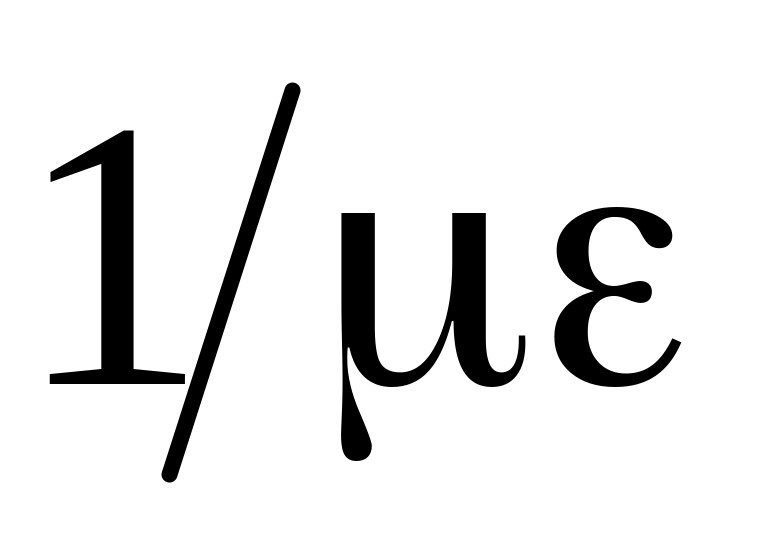
и 
в обоих уравнениях имеют одинаковые размерности, так как в цепях с распределенными параметрами эти параметры задаются на единицу длины линии:
Выражение для волн тока в линии мы получали с помощью волнового сопротивления:
,
здесь через Z обозначено волновое сопротивление линии без потерь, которое по аналогии эквивалентно волновому сопротивлению идеального диэлектрика для электромагнитных волн:
.
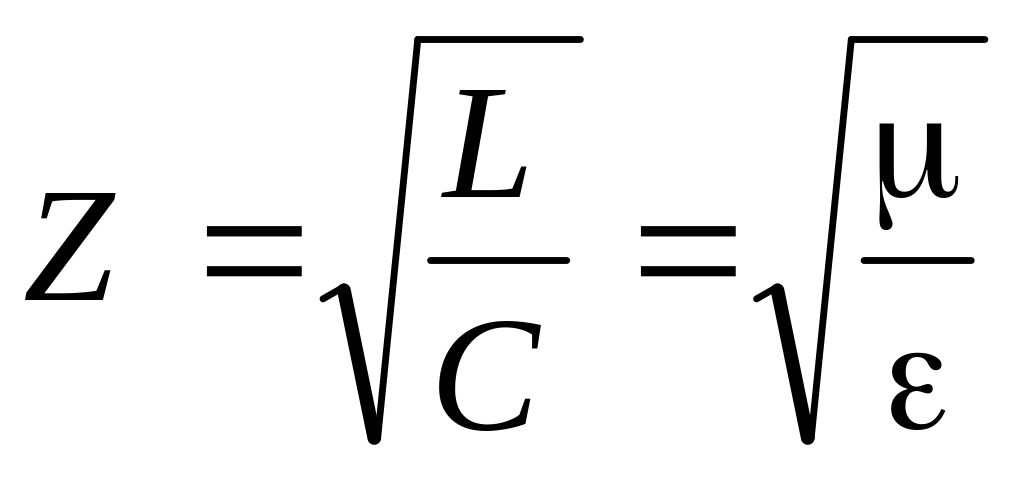
Применив аналогичное преобразование для решения волнового уравнения относительно напряженности электрического поля, получим решения для напряженности магнитного поля:
.
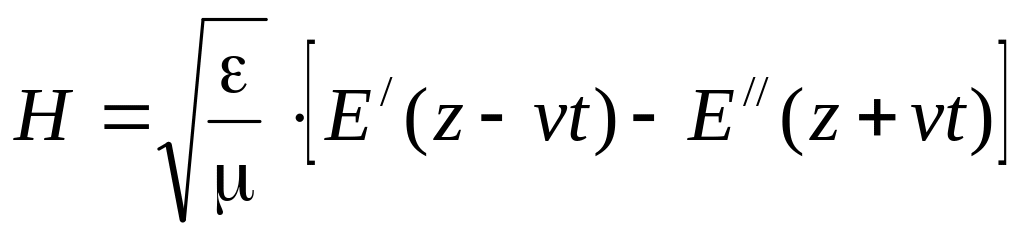
Полученные решения означают, что векторы E и H в любой точке переменного электромагнитного поля взаимно перпендикулярны, связаны между собой через волновое сопротивление, а электромагнитные волны распространяются в диэлектрике со скоростью v, которая называется скоростью света и в пустоте равна:
В любых диэлектриках ≥0 и ≥0, поэтому скорость распространения электромагнитных волн в них меньше или равна скорости света в пустоте vc.
Волновое сопротивление, связывающее между собой напряженности электрического и магнитного поля в прямой и обратной волнах:
,
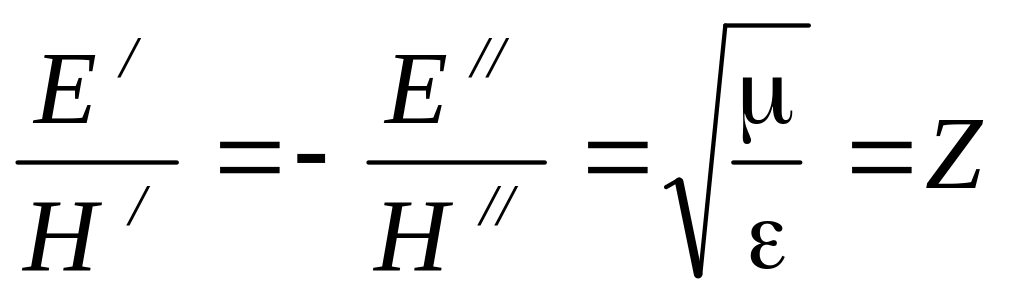
также зависит от свойств диэлектрика и для пустоты равно:
Ом
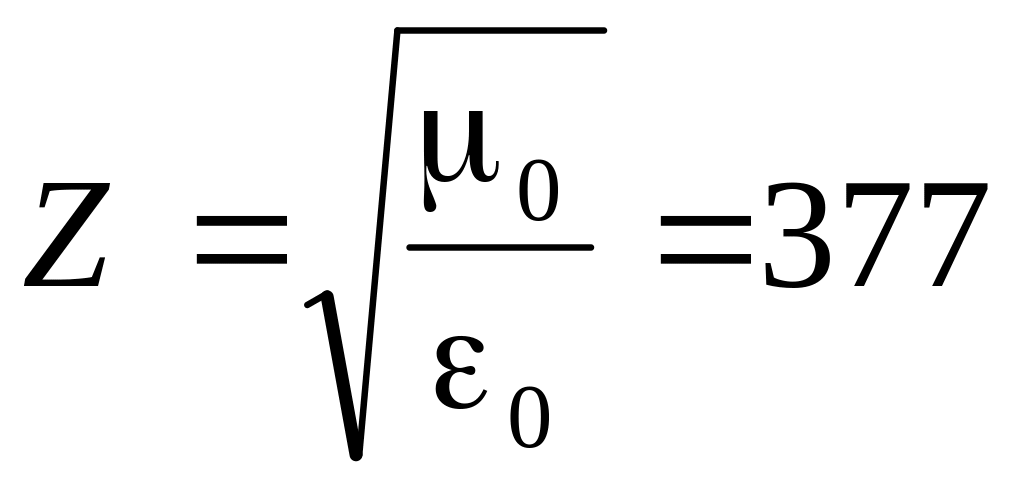
Для прямой (или обратной) волны в отдельности можем записать соотношение:
; 
; 
.
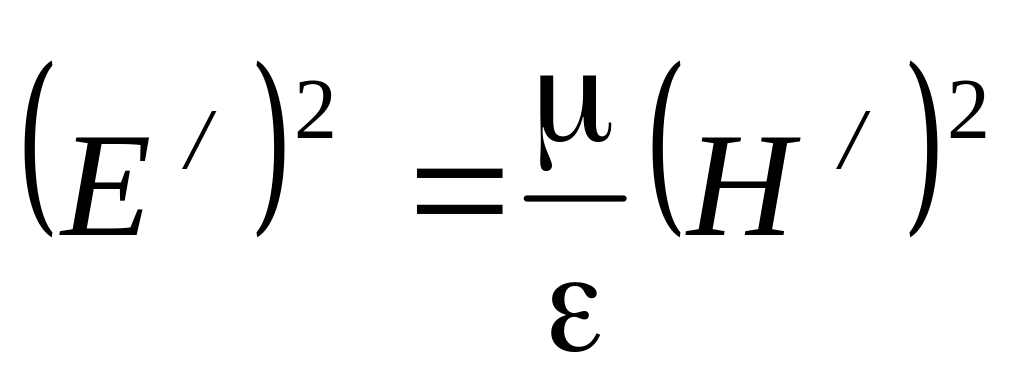
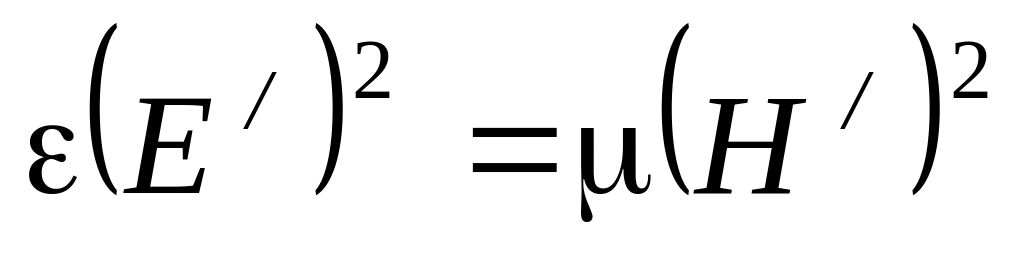
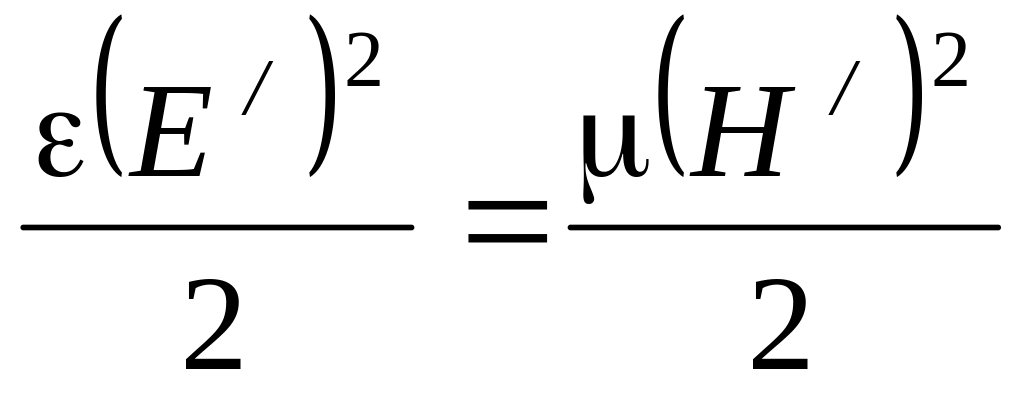
Это означает, что плотности энергии электрического и магнитного поля в любой точке для прямой (или обратной) электромагнитной волны равны друг другу:
.
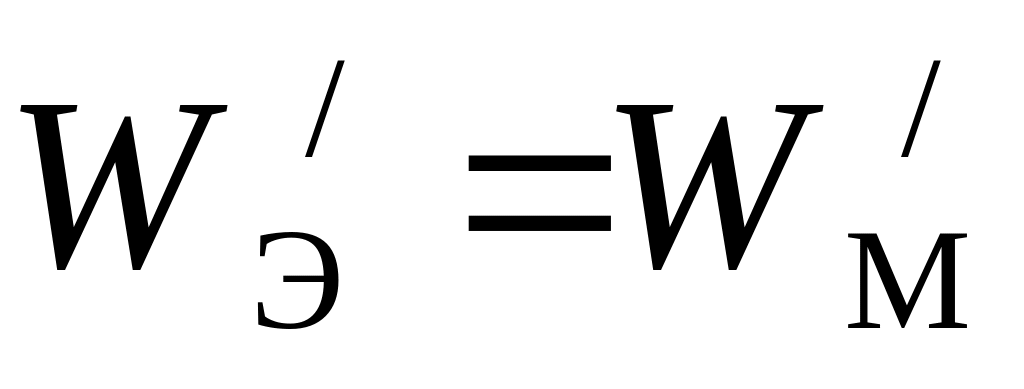
Для электромагнитных волн в идеальном диэлектрике можно использовать по аналогии все ранее полученные соотношения для бегущих волн в однородной линии без потерь. В частности, справедливы формулы для определения отраженной и преломленной волн на границе диэлектриков с различными волновыми сопротивлениями. При этом соблюдаются все граничные условия для составляющих векторов напряженности электрического и магнитного поля. Вообще, решение волнового уравнения может быть получено, если заданы граничные и начальные условия для векторов.
Переменное электромагнитное поле в однородном изотропном диэлектрике и полупроводящей среде
4.1. Уравнения Максвелла для переменного электромагнитного поля в идеальном однородном изотропном диэлектрике имеют вид:
1. 2. 3.
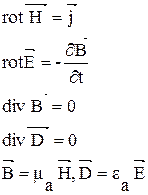
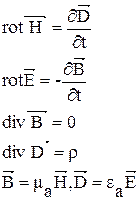
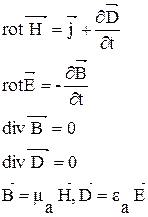
4.2. Для диэлектриков справедливо соотношение:
1. 
. 2. 
. 3. 
.
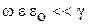
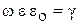
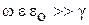
Здесь ω – частота электромагнитного поля, γ – удельная электрическая проводимость среды, ε – относительная диэлектрическая проницаемость среды.
4.3. Электрическая и магнитная компоненты падающей гармонической электромагнитной волны в изотропной диэлектрической среде описываются формулами:
1. 
. 2. 
.
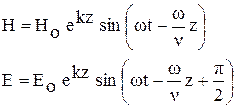
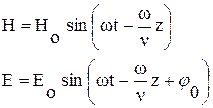
3. 
.
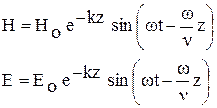
4.4. Амплитуда электромагнитной волны, распространяющейся в идеальном диэлектрике:
1. Уменьшается. 2. Увеличивается. 3. Не меняется.
4.5. Плоская электромагнитная волна распространяется в среде, состоящей из двух диэлектриков. На границе раздела диэлектрических сред для электрической и магнитной компоненты волны выполняются условия:
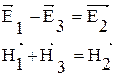
1. Линейно. 2. По кругу. 3. По эллипсу.
4.7. Волновое сопротивление идеальной диэлектрической среды является числом:
4.8. При отражении электромагнитной волны от границы раздела между диэлектриком (воздух) и проводником (медь) фаза электрической компоненты плоской электромагнитной волны меняется на:
4.9. Явление полного преломления наблюдается при падении на границу раздела двух диэлектрических сред под углом Брюстера плоской электромагнитной волны:
1. Перпендикулярно поляризованной.
2. Параллельно поляризованной.
3. Поляризованной по кругу.
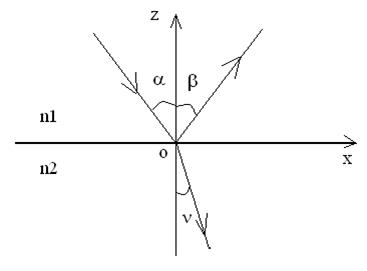
4.10. Законы Снеллиуса для плоской электромагнитной волны имеют следующий вид:
1. 
. 2. 
. 3. 
.
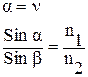
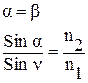
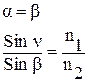
4.11. Углом полного внутреннего отражения (предельным углом) называется угол падения электромагнитной волны на границу раздела двух диэлектрических сред, определяемого выражением:
, где
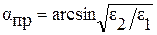
Здесь ε – относительная диэлектрическая проницаемость, μ – относительная магнитная проницаемость среды.
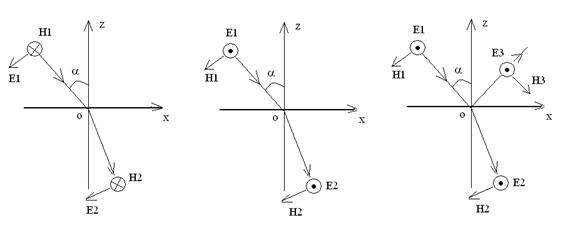
4.13. На каком из рисунков правильно показано полное преломление плоской линейно поляризованной электромагнитной волны?
Кружки с точкой или крестиком означают векторы, направленные соответственно к читателю или от него, α – угол Брюстера.
4.14. Параллельно поляризованная электромагнитная волна падает из первой диэлектрической среды (ε = 4, μ = 1) во вторую диэлектрическую среду (ε = 1, μ = 1). При каком угле падения на границу раздела диэлектриков будет отсутствовать отраженная волна (полное преломление)?
Здесь ε – относительная диэлектрическая проницаемость, μ – относительная магнитная проницаемость среды.
4.15. Дифракция электромагнитной волны наблюдается при выполнении соотношения для длины волны λ и размера тела а:
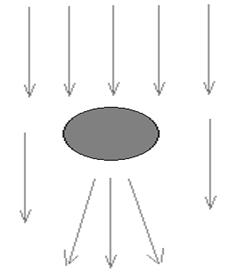
4.16. Появление за проводящим телом интенсивного электромагнитного поля связано:
1. Прохождением падающей электромагнитной волны.
2. Возникновением на поверхности проводящего тела вихревых токов, являющихся источником вторичных электромагнитных волн.
3. Наложением электромагнитных волн, огибающих проводящее тело с двух сторон.
4.17. Для устранения отражения электромагнитной волны, падающей на границу раздела двух диэлектриков, между ними помещают слой третьего диэлектрика толщиной:
Здесь λ – длина электромагнитной волны.
4.18. Для полупроводящих сред справедливо соотношение (при достаточно высоких частотах электромагнитной волны):
1. . 2. . 3. .
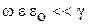
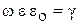
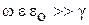
Здесь ω – частота электромагнитного поля, γ – удельная электрическая проводимость среды, ε – относительная диэлектрическая проницаемость среды.
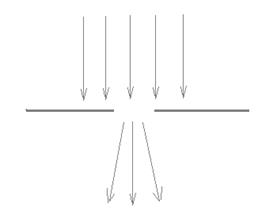
4.19. Появление за щелью в проводящем экране интенсивного электромагнитного поля связано:
1. Прохождением падающей электромагнитной волны.
2. Возникновением на поверхности проводящего экрана вихревых токов, являющихся источником вторичных электромагнитных волн.
3.Прохождением части волнового фронта падающей электромагнитной волны.
4.20. Параметр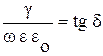 
называется тангенсом угла диэлектрических потерь. Для идеального диэлектрика он равен:
1. Не более 0.01. 2. Более 100. 3. Меняется от 0.01 до 100.
Здесь ω – частота электромагнитного поля, γ – удельная электрическая проводимость среды, ε – относительная диэлектрическая проницаемость среды.
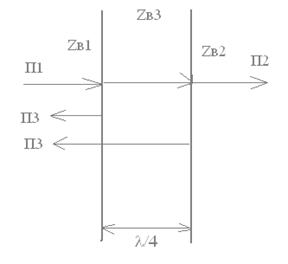
4.21. Метод устранения отражения электромагнитной волны П1, падающей на границу раздела двух диэлектриков с волновыми сопротивлениями Zв1 и Zв2, между которыми расположен слой третьего диэлектрика с волновым сопротивлением Zв3, основан на том, что в диэлектрической среде 1 происходит наложение отраженных волн П3, отстоящих друг от друга на фазу:
4.22. При распространении линейно поляризованной электромагнитной волны в гиротропной среде наблюдается:
а) вращение плоскости поляризации по часовой стрелке,
б) вращение плоскости поляризации против часовой стрелки,
в) отсутствие вращения плоскости поляризации.
4.23. Вращение плоскости поляризации линейно поляризованной электромагнитной волны при распространении в гиротропной среде связано:
1. С изотропностью диэлектрической и магнитной проницаемости среды.
2. С анизотропностью диэлектрической и магнитной проницаемости среды.
3. С тензорным характером диэлектрической и магнитной проницаемости среды.
Переменное электромагнитное поле в диэлектрике
В переменном электромагнитном поле наблюдаются одновременно обе, рассмотренные ранее нами в отдельности, его стороны. Связь между ними дают первое и второе уравнения Максвелла – закон полного тока и закон электромагнитной индукции:
, 
.
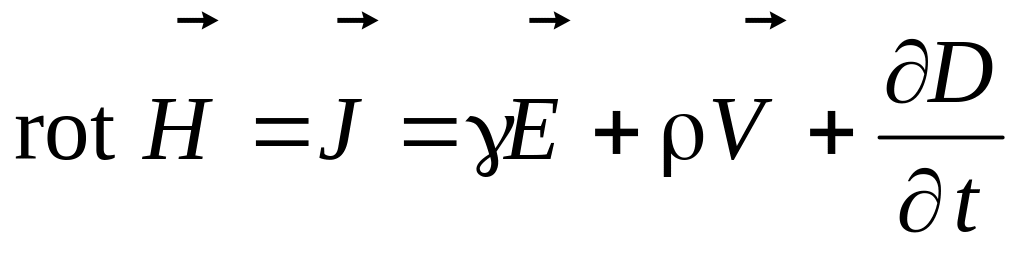
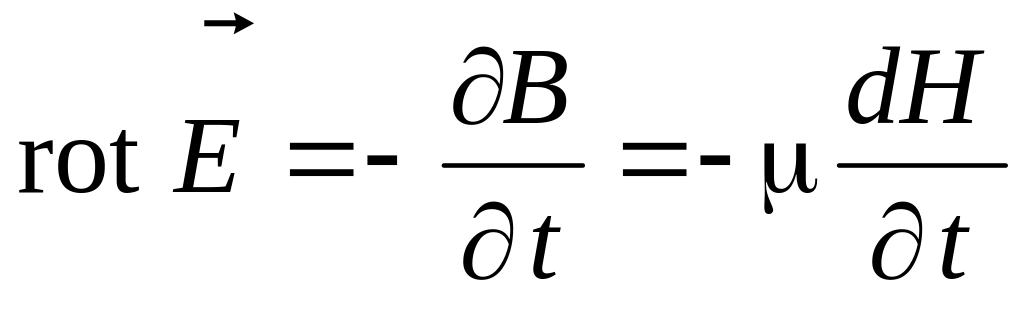
Анализируя переменное электромагнитное поле в диэлектрике, считаем диэлектрик идеальным (=0) и предполагаем отсутствие в нем объемных зарядов (=0). Тогда:
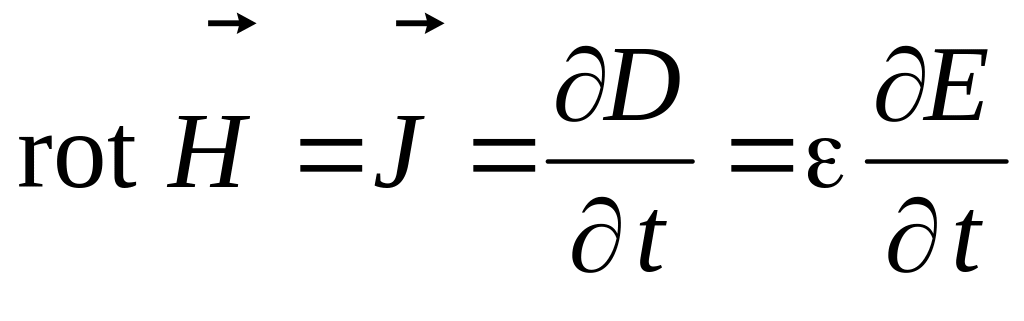
Запишем оба уравнения в проекциях на оси декартовой системы координат:
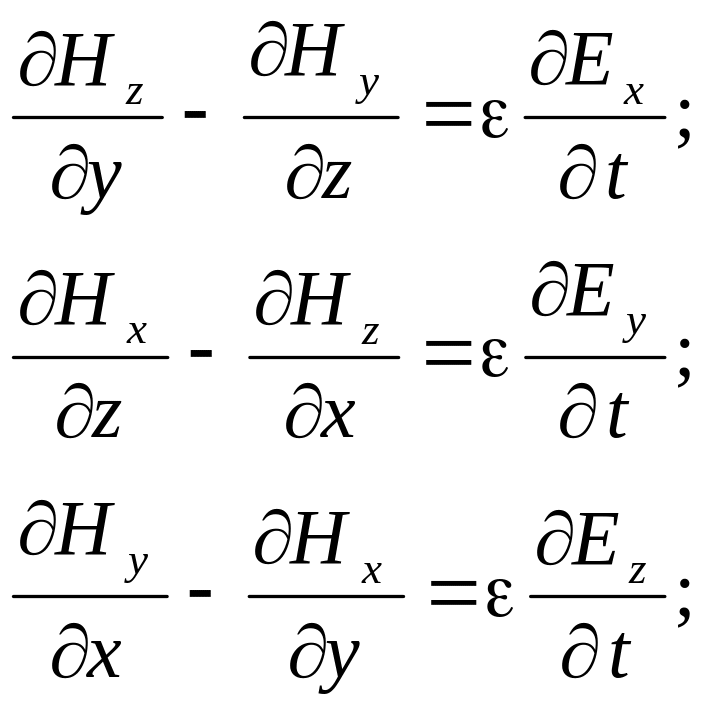
В плоской электромагнитной волне производные от любых проекций векторов поля по координатам x и y равны нулю, поэтому система уравнений упрощается и принимает вид:
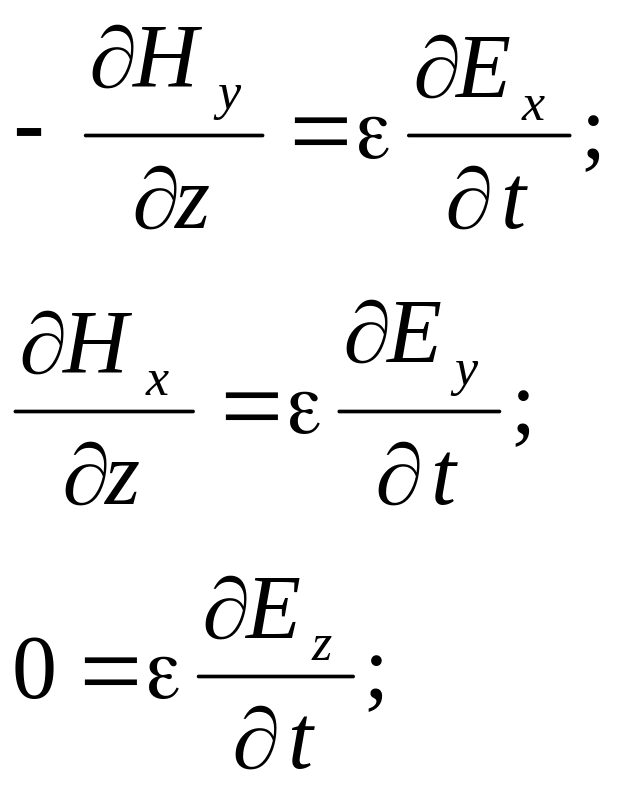
Из последних уравнений каждой системы ввиду равенства нулю производных получаем, что проекции векторов Ez и Hz не зависят от времени: Ez=const и Hz=const. Принимаем их равными нулю, так как переменное поле, излученное антенной, не содержит постоянных составляющих. Кроме того, мы уже рассматривали ранее постоянные электрические и магнитные поля, и в случае необходимости можем, если потребуется учесть их вместе с переменным полем, применив принцип наложения.
Рассматривая оставшиеся четыре уравнения для проекций, направим ось x декартовой системы координат вдоль вектора напряженности электрического поля (Ey=0). В этом случае остается единственная составляющая вектора напряженности электрического поля: E=Ex. В этом случае уравнения еще больше упрощаются:
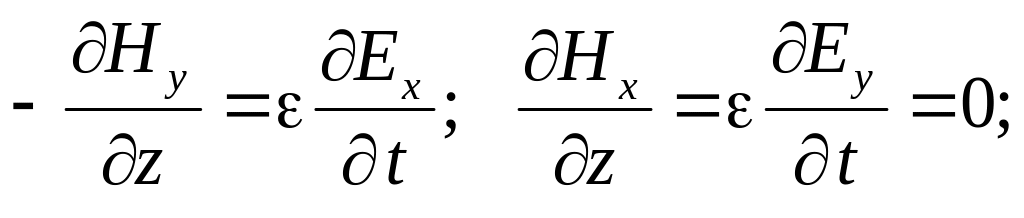
Из полученных уравнений следует, что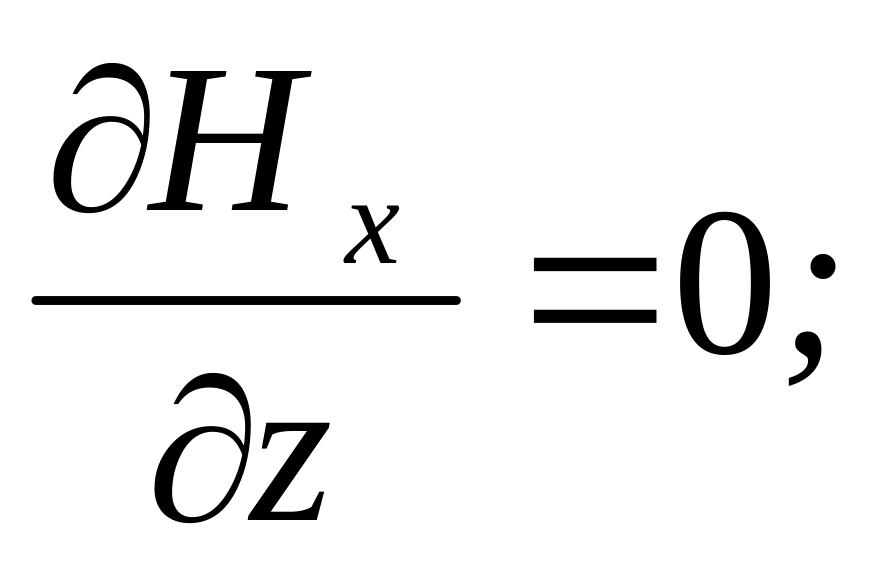 
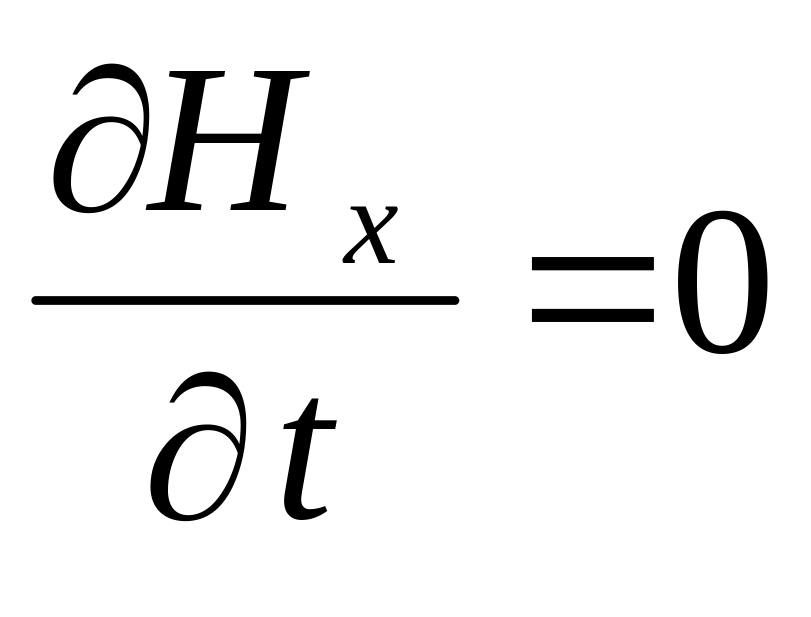
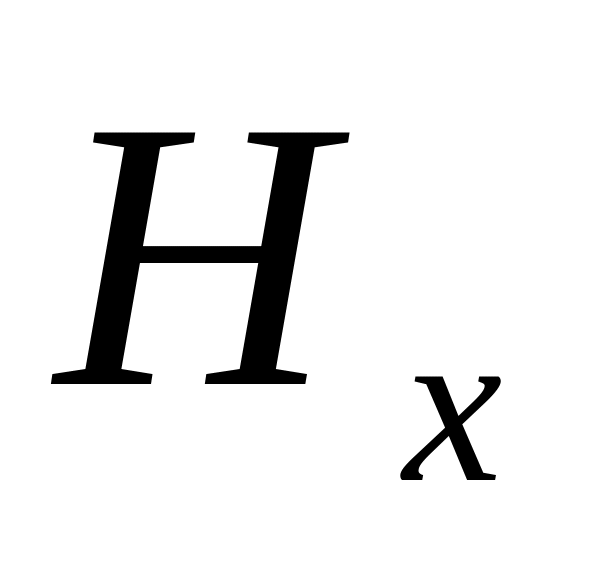
, т.е. 
=const=0,
и при выбранном направлении осей координат, вектор напряженности магнитного поля имеет лишь единственную составляющую, направленную вдоль оси y: H=Hy. Это означает, что в плоско поляризованной электромагнитной волне в диэлектрике в любой точке векторы напряженности электрического и магнитного поля расположены взаимно перпендикулярно.
Н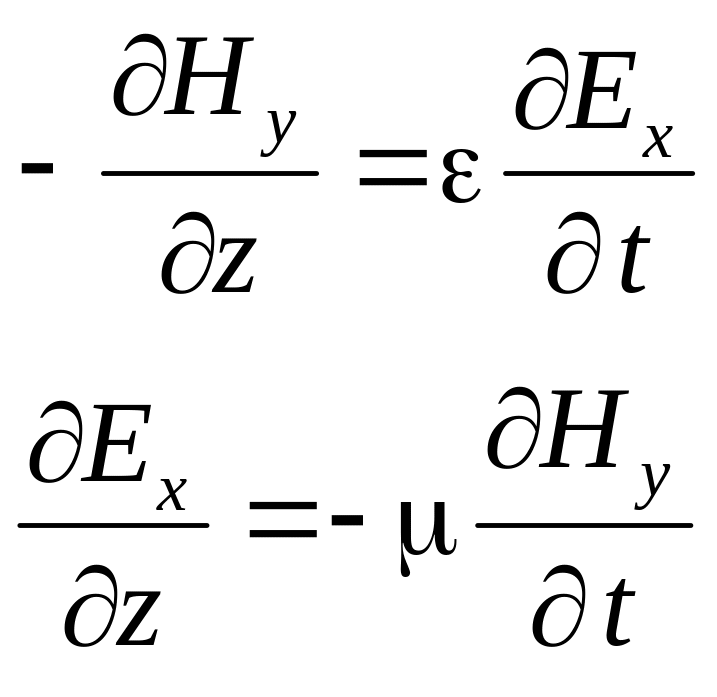 
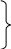
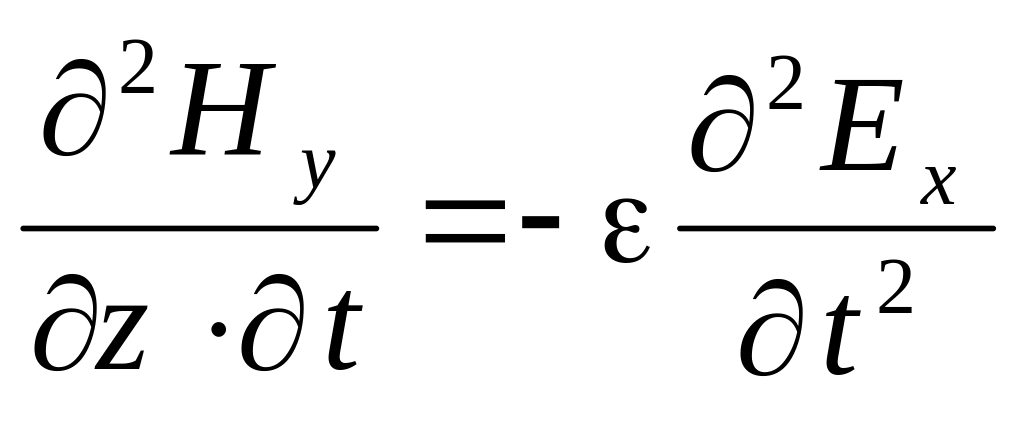
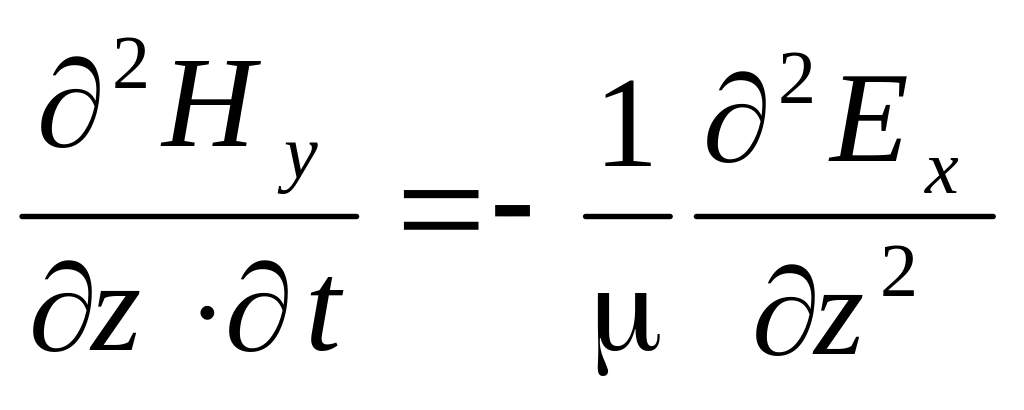
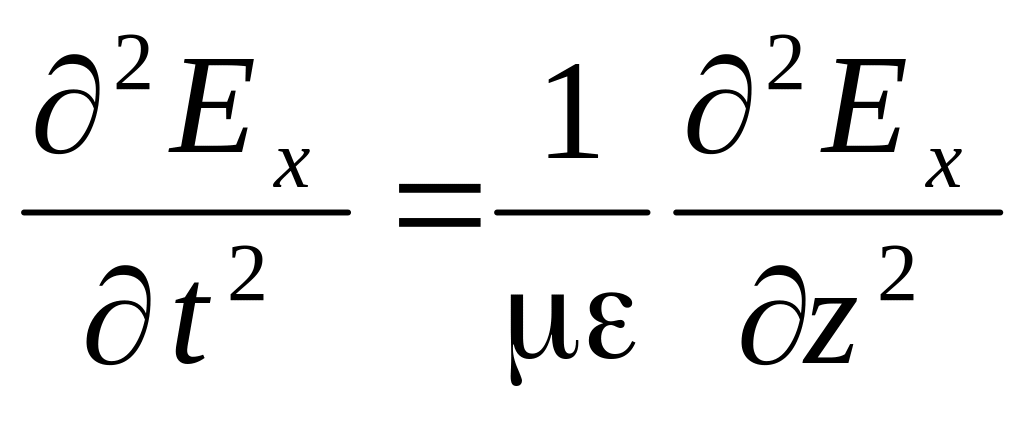
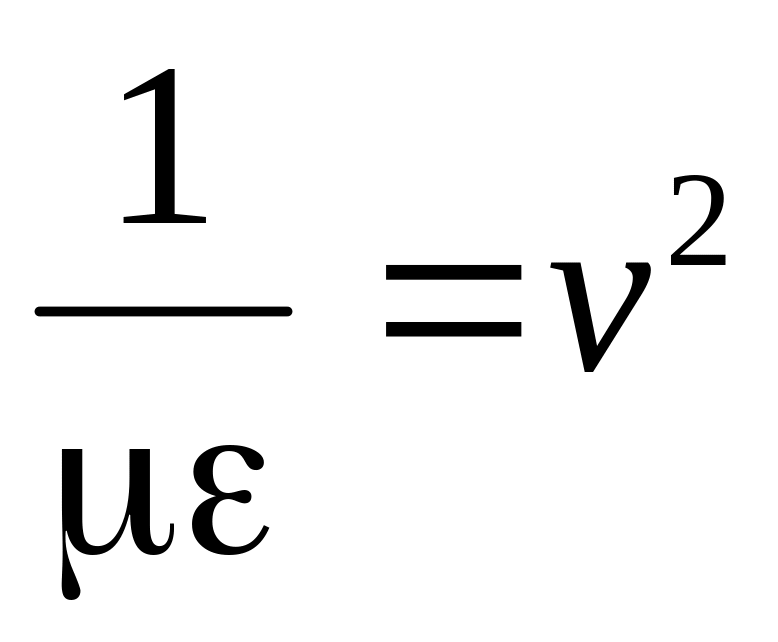
айдем решение системы двух оставшихся уравнений:
Д 
ифференцируя первое уравнение по времени, а второе по координате z, получим:
; 
, откуда: 
, и обозначив 
, запишем уравнение для вектора напряженности электрического поля, которое называется волновым уравнением:
При рассмотрении режимов в цепях с распределенными параметрами нами были получены аналогичные уравнения для напряжения в произвольной точке линии без потерь, в которой координата x отсчитывается от начала линии:
.
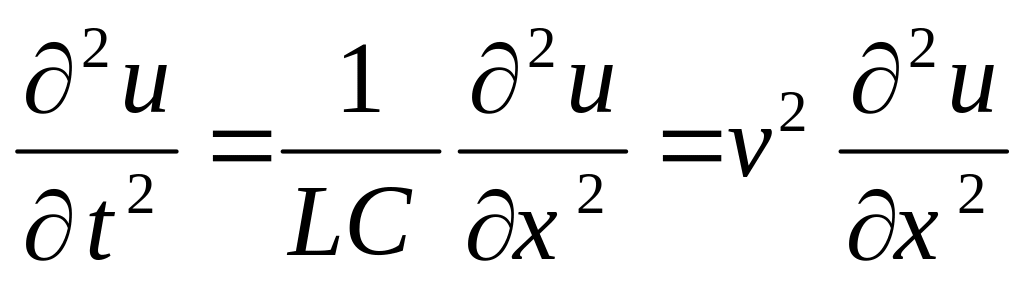
Решение для волнового уравнения в линии мы получили в виде суммы прямой и обратной бегущих волн напряжения:
Решение для напряженности электрического поля запишем по аналогии:
Коэффициенты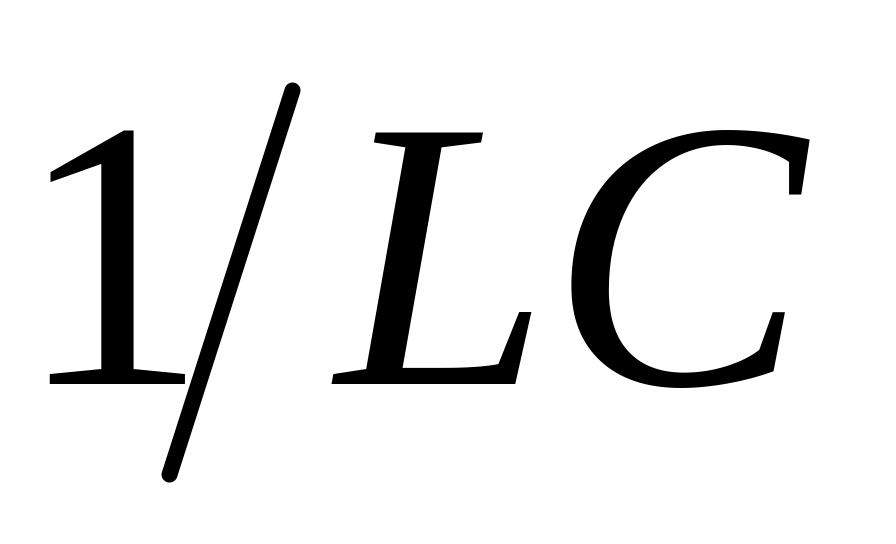 
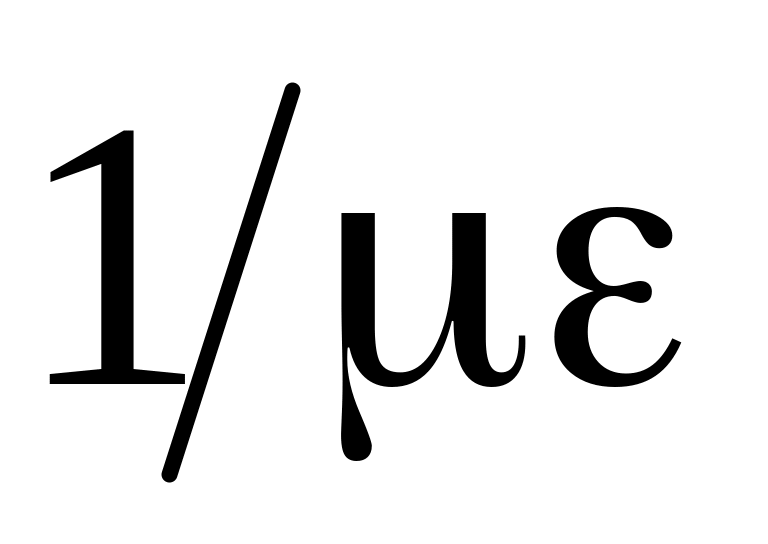
и 
в обоих уравнениях имеют одинаковые размерности, так как в цепях с распределенными параметрами эти параметры задаются на единицу длины линии:
Выражение для волн тока в линии мы получали с помощью волнового сопротивления:
,
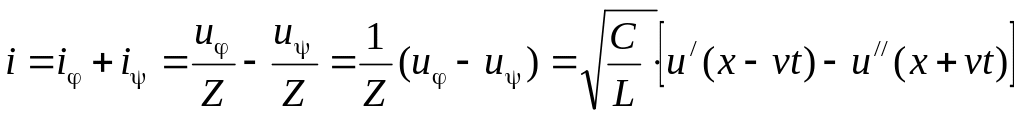
здесь через Z обозначено волновое сопротивление линии без потерь, которое по аналогии эквивалентно волновому сопротивлению идеального диэлектрика для электромагнитных волн:
.
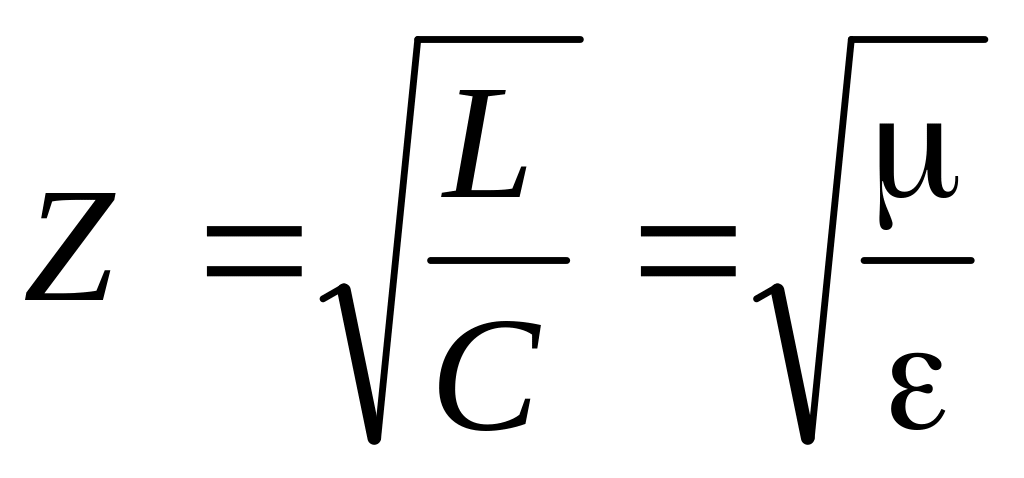
Применив аналогичное преобразование для решения волнового уравнения относительно напряженности электрического поля, получим решения для напряженности магнитного поля:
.
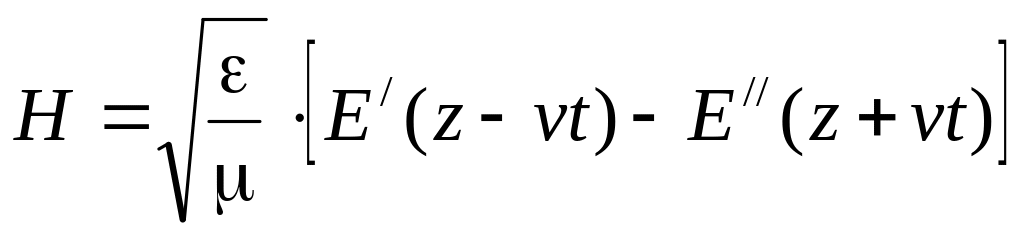
Полученные решения означают, что векторы E и H в любой точке переменного электромагнитного поля взаимно перпендикулярны, связаны между собой через волновое сопротивление, а электромагнитные волны распространяются в диэлектрике со скоростью v, которая называется скоростью света и в пустоте равна:
В любых диэлектриках ≥0 и ≥0, поэтому скорость распространения электромагнитных волн в них меньше или равна скорости света в пустоте vc.
Волновое сопротивление, связывающее между собой напряженности электрического и магнитного поля в прямой и обратной волнах:
,
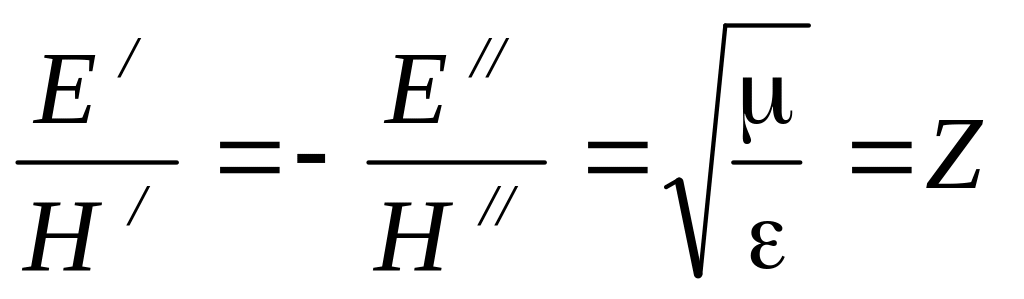
также зависит от свойств диэлектрика и для пустоты равно:
Ом
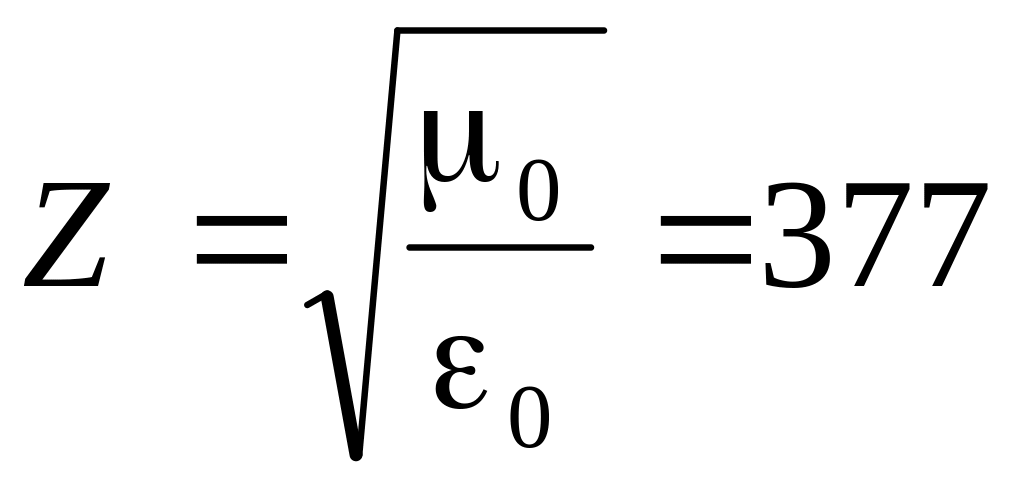
Для прямой (или обратной) волны в отдельности можем записать соотношение:
; 
; 
.
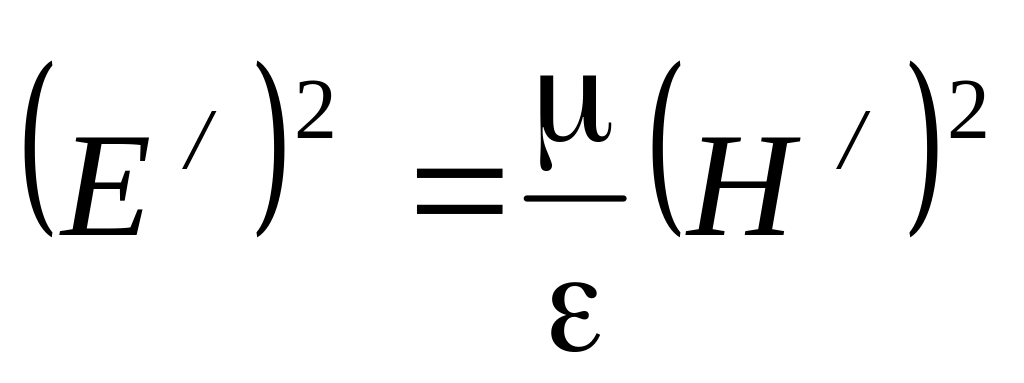
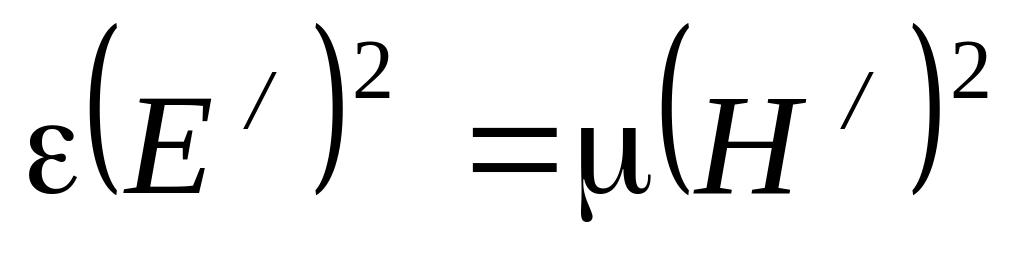
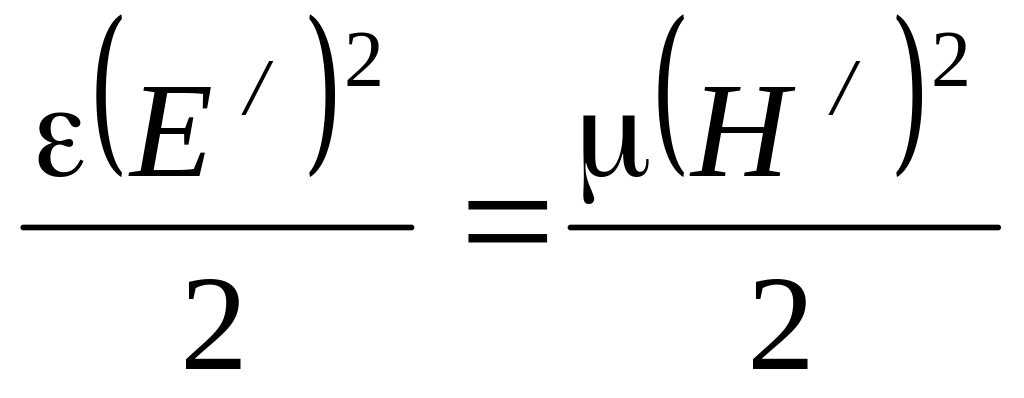
Это означает, что плотности энергии электрического и магнитного поля в любой точке для прямой (или обратной) электромагнитной волны равны друг другу:
.
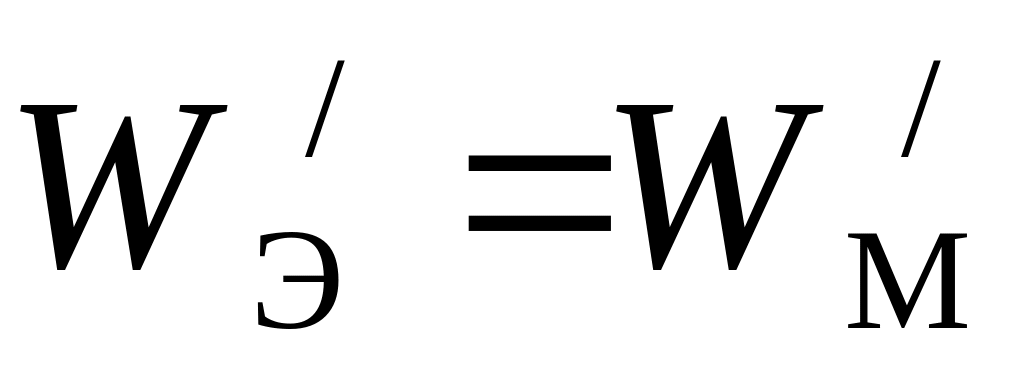
Для электромагнитных волн в идеальном диэлектрике можно использовать по аналогии все ранее полученные соотношения для бегущих волн в однородной линии без потерь. В частности, справедливы формулы для определения отраженной и преломленной волн на границе диэлектриков с различными волновыми сопротивлениями. При этом соблюдаются все граничные условия для составляющих векторов напряженности электрического и магнитного поля. Вообще, решение волнового уравнения может быть получено, если заданы граничные и начальные условия для векторов.