парадокс с тремя дверями
Проблема Монти Холла
Парадокс, который противоречит интуитивному восприятию, но объясняется теорией вероятностей.
Ранее в статье «Парадоксы и вероятность» уже давалось математическое объяснение некоторым противоречиям, которые не поддаются логическому или интуитивному восприятию.
Одним из таких парадоксов также является Проблема Монти Холла. Возможно вы о ней уже слышали или читали, например, в романе Сергея Лукьяненко «Недотёпа», или видели в фильме «Двадцать одно».
В этом фильме герой актера Кэвина Спейси — профессор MIT Микки Роса предлагает своему студенту Бену Кэмпбеллу решить задачу: имеется три двери, за двумя из которых находится по самокату, а за одной — автомобиль; необходимо угадать дверь с автомобилем. После того, как Бен сделал свой выбор на первой двери, Микки открыл третью дверь, за которой оказался самокат и предложил Бену изменить свой первоначальный выбор. Бен соглашается это сделать и математически аргументирует свое решение. Таким образом он проходит тест и попадает в команду Микки, которая обыгрывает казино, разработав план на основе теории вероятностей, посредством которого вероятность выигрыша при игре в блэкджек (двадцать одно) увеличивается в несколько раз.
Задача Микки Роса — это и есть Проблема Монти Холла.
Она названа в честь ведущего американской телеигры “ Let’s Make a Deal” («Сделай сделку») Монти Холла ( Monty Hall).
Американская писательница и журналист Мэрилин вос Савант ( Marilyn vos Savant), кстати занесённая в Книгу рекордов Гиннесса как обладательница самого высокого в мире IQ, в своей рубрике «Спросите у Мэрилин» в журнале Parade еще в 1990 году так описала эту проблему:
Предположим, вы участвуете в игровом шоу и вам предлагают сделать выбор из трех дверей: за одной дверью стоит автомобиль; за другими — козы. Вы выбираете дверь, например, №1, после этого ведущий шоу, который знает, что находится за дверьми, открывает одну из двух оставшихся, например, №2, за которой оказывается коза. Затем он говорит вам: «Вы хотите выбрать дверь №3?». Выгодно ли вам изменить свой выбор?
Это невероятно трудная и противоречивая проблема!
Вот что написал об этом недавно экономист Тим Харфорд ( Tim Harford) в Financial Times:
Забудьте последнюю теорему Ферма. Самой острой проблемой в математике является проблема Монти Холла. Монти Холл — урожденный Монте Гальпарин (Monte Halparin) — провел около 5000 выпусков американского игровое шоу «Сделай сделку» (Let’s Make a Deal), которое вдохновило эту загадку. Это головоломка — лук, «раздевая» который слой за слоем, вы будете плакать.
Итак, представьте, что вы находитесь на шоу Монти Холла и перед вами стоят три двери, за одной из которых находится автомобиль, а за двумя другими — козы.
Ведущий шоу Монти предлагает сделать вам выбор одной из дверей и, если за ней окажется автомобиль, то вы его получите.
Разумеется, что первоначально вероятность того, что машина находится за любой из дверей равняется 1/3 или около 33,3%.
Вы выбираете случайную дверь, например, №1. Как мы отметили выше, вероятность того, что автомобиль стоит за этой дверью, составляет 1/3 или примерно 33,3%.
Очевидно, что вероятность того, что он окажется за оставшимися двумя дверьми будет 2/3 или примерно 66,6%.
Монти знает, за какой дверью находится автомобиль, а за какими — козы, и он открывает одну из других дверей, показывая козу.
Монти спрашивает, хотите ли вы после этого изменить свой первоначальный выбор и выбрать дверь №3?
Интуитивно кажется, что вероятности нахождения автомобиля за первой и за третьей дверьми одинаковы — 1/2. И нет особого смысла менять свой первоначальный выбор.
Но, с другой стороны, в сценарии ничего не изменилось. Вероятность того, что ваш первоначальный выбор правильный, равен 1/3. А шансы, что автомобиль стоит за другими дверьми, по-прежнему составляют 2/3. Но теперь, благодаря Монти, осталась только одна закрытая дверь.
Поэтому, конечно, вы должны изменить свой выбор, — показывая вам, что за одной из двух оставшихся дверей нет автомобиля, Монти просто удвоил ваш шанс.
Большинство людей неизбежно и безнадежно обманывают себя, думая, что шансы 50/50 только потому, что осталось две закрытых двери. Они рассматривают ситуацию начиная с этого момента, не учитывая предыдущий этап.
Но если вы посмотрите на ситуацию последовательно, как было показано выше, то правильный ответ становится интуитивно понятен — нужно изменить свой первоначальный выбор, тем самым удвоив свои шансы.
Попробуем посмотреть на эту проблему по-другому. Представьте, что три человека выбрали первоначально каждый по одной двери — №1, №2 и №3.
Если они не изменят своего решения после того, как будет открыта одна дверь с козой, то только один из них выиграет — тот, кто первоначально выбрал дверь №1.
Если же после того, как останется только две двери, они поменяют свой первоначальный выбор, то в выигрыше будут уже два человека — те, кто выбрали сначала двери №2 и №3.
Следовательно при изменении решения после того, как остается только две двери, вероятность выигрыша возрастает вдвое!
Одним из объяснений этого является следующее: если игрок меняет свой выбор после действий ведущего, то он выигрывает, если первоначально выбрал проигрышную дверь. А вероятность этого вдвое выше, чем выбор выигрышной двери, поскольку автомобиль один, а козы две.
Если же и это вас не убедило, попробуем составить таблицу всех вариантов:
Как видно из таблицы, вероятность выигрыша при смене первоначального выбора вдвое выше, чем при сохранении его.
Разумеется, все вышесказанное справедливо для случая, когда ведущий во-первых, знает, что за какой дверью находится, во-вторых, открывает только дверь, которую не выбрал первоначально игрок и за этой дверью всегда должна быть коза.
Если у вас еще остались сомнения, поэкспериментируйте с Симулятором парадокса Монти Холла.
В заключение посмотрите эти два видео о Проблеме Монти Холла.
Простейшее объяснение парадокса Монти Холла
Парадокс Монти Холла — это одна из тех математических задач, над решением которой уже долгое время бьются многие умы, и даже всемирно известных математиков она приводит в затруднение. Хотя идея, лежащая в основе этого парадокса, предельно ясна и понятна. Задача эта, строго говоря, и не парадокс вовсе, но называется так из-за неочевидности и парадоксальности предлагаемых решений и объяснений, которые становятся поводом для самых жарких дискуссий в Интернете. Их накал уступает, пожалуй, лишь спорам из-за оптической иллюзии так называемого «платья раздора» и аудиоиллюзии «Янни и Лорел». Предлагаемое здесь объяснение призвано раз и навсегда развеять все связанные с этим парадоксом вопросы и очень доходчиво разъяснить всем интересующимся его суть.
Парадокс
Парадокс впервые был сформулирован американским математиком Стивом Селвином ещё в 1975 году, но широкую известность он приобрёл благодаря популярному игровому шоу «Давайте заключим сделку». В честь ведущего этой телевикторины, которого звали Монти Холл, парадокс и получил своё название.
В чём же суть парадокса Монти Холла?
Представьте, что перед вами три двери, как показано на рисунке ниже. За двумя дверьми находятся козы, за одной — автомобиль. Надо угадать дверь с автомобилем, и он ваш.
Казалось бы, ничего сложного. Но, как говорилось в одном фильме: «Если бы задача так просто решалась, то армянское радио этим бы не занималось». В своей передаче, после того как участник выбирал дверь, Монти всегда открывал одну из дверей с козой и предлагал ему поменять свой выбор. А вы поменяли бы или нет?
Этот вопрос многих ставит в тупик. Люди обычно думают: «Ну какая разница: остались две двери, и машина может с одинаковой вероятностью 50% оказаться как за одной, так и за другой дверью?». … И оказываются неправы. Правильный ответ — всегда менять первоначальный выбор. Поступая так, вы удваиваете свои шансы на победу.
Удивлены? Такой ответ для многих становится откровением: мало кто ожидает этого. Давайте подробно разберёмся, как так получается.
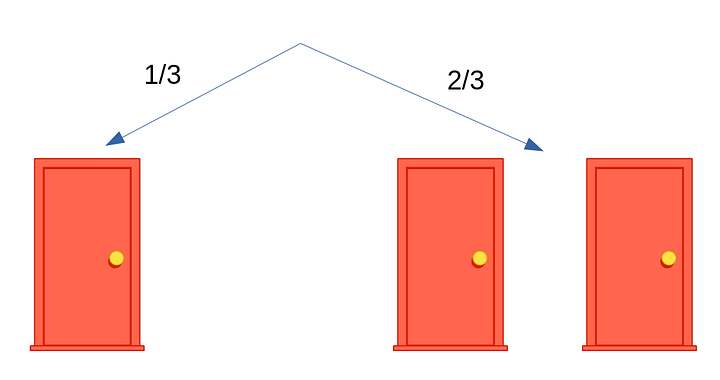
Итак, вы выбрали одну из трёх дверей. Вероятность того, что машина окажется именно за ней, составляет 1/3. А вероятность того, что она окажется за одной из двух оставшихся (то есть не выбранных вами) дверей, будет 2/3. Это должно быть понятно.
На рисунке у нас наглядно показаны эти вероятности: 1/3 слева и 2/3 справа.
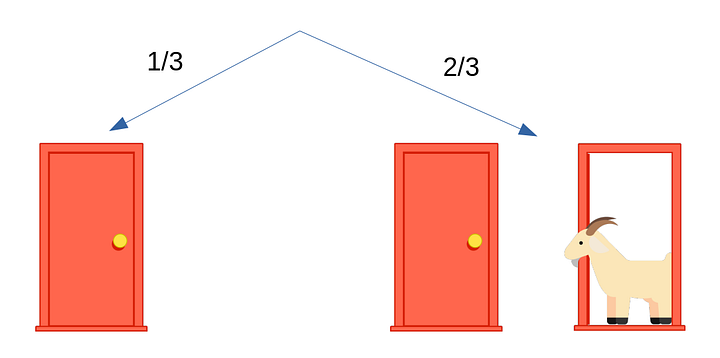
Теперь Монти открывает одну из невыбранных дверей — тех, что справа. И открывает он всегда ту, за которой коза.
Вероятности остаются неизменными: 1/3 слева (ваш первоначальный выбор) и 2/3 справа. Изменилось лишь то, что справа одна дверь теперь открыта, но вероятность для оставшейся неоткрытой двери здесь та же, что была прежде для обеих.
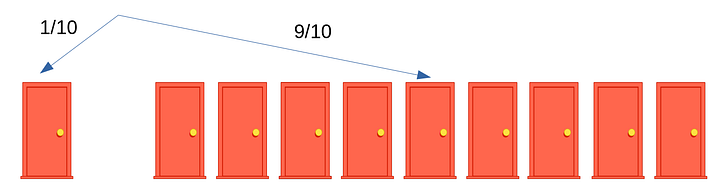
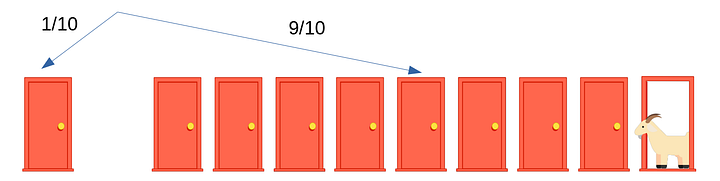
Если не совсем понятно, попробуем объяснить на примере с десятью дверьми.
Выбранная вами дверь будет слева, остальные девять — справа (как на рисунке ниже). Вероятность того, что вы угадали дверь с машиной, будет 1/10. Вероятность того, что вы не угадали и машина окажется за одной из оставшихся девяти дверей, будет 9/10.
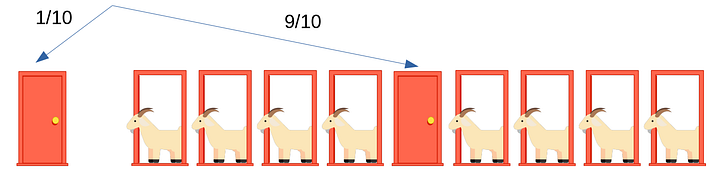
Дальше Монти открывает восемь из этих невыбранных девяти дверей, причем за всеми восемью — козы. Как поступить теперь: поменять свой выбор или нет? Конечно, поменять! Ведь теперь восемь из девяти дверей справа открыты, а вероятность того, что машина окажется за оставшейся девятой дверью (как мы уже посчитали ранее), равна 9/10.
Ответ на вопрос станет ещё очевиднее, если представить, что Монти даёт вам возможность открыть не одну оставшуюся справа неоткрытой дверь, а сразу все девять!
Вот и всё. Это так просто! Однако важно не забывать, что всегда есть вероятность проигрыша. Верное решение определяется стратегией. Правильная стратегия — делать так, чтобы шансы на победу были максимальными или хотя бы такими, которые позволяют больше выигрывать, чем проигрывать.
Усложняем задачу
Предположим, Монти хочет усложнить для вас задачу и открывает лишь одну дверь с правой стороны. Как вы поступите теперь: выберите одну из восьми закрытых дверей справа или не станете менять свой выбор?
Здесь придётся кое-что посчитать. Вероятность того, что машина окажется за одной из девяти дверей справа, равна 9/10. Разделим её на количество оставшихся неоткрытыми дверей (8):
Это будет вероятность того, что машина окажется за одной из восьми остающихся закрытыми дверей справа. И она чуть больше вероятности 0,1 (1/10), что первоначально выбранная вами дверь слева окажется с машиной. Поэтому вам всё же предпочтительнее поменять свой выбор, хотя шансы выиграть машину и в этом случае будут очень низкими. По этой же формуле можно посчитать вероятность для любого количества неоткрытых дверей.
Вот и весь парадокс Монти Холла вкратце. Не знаю, можно ли придумать более простое его объяснение? Я лишь выношу на ваш суд свой взгляд, отличный от тех, что изложены в большинстве других объяснений, в которых вы можете тоже почерпнуть много полезного. Надеюсь, что после прочтения статьи вы приблизились к пониманию парадокса Монти Холла.
Снова про Монти Холла или статистика как коллективная интуиция
На примере парадокса Монти Холла посмотрим, что общего между статистикой и интуицией, и как визуализация данных может помочь принять правильное решение, основанное на статистической оценке.
Сложность парадокса Монти Холла
Парадокс Монти Холла получил свое название от ведущего телевизионного шоу «Let’s Make a Deal». Игровая ситуация:
Перед игроком три двери, за одной из которых приз. Игрок выбирает одну из них, не открывая. После этого ведущий, открывает одну из двух оставшихся дверей. Ведущий знает, за какой из дверей приз, и всегда открывает дверь, за которой приза нет. Далее игроку предлагается поменять первоначально выбранную дверь на другую, остающуюся закрытой. Вопрос: повышаются ли шансы игрока при изменении выбранной двери?
Парадокс заключается в том, что интуитивно кажется, что смена двери ничего не дает. Приз либо за одной дверью, либо за другой. Ситуация симметричная, и вероятности одинаковы. Однако, теория вероятностей показывает, что смена двери повышает шансы выигрыша в два раза.
Чтобы прийти к статистически правильному решению, игрок должен:
Первый шаг ключевой. Если остаться на уровне выбора дверей, то ничего не получится, ведь приз, так или иначе, за одной из двух дверей. А они выглядят одинаково — ситуация как будто симметричная. Можно не менять дверь и выиграть, можно поменять дверь и проиграть. Возможно, смена двери повышает шансы на успех, но не гарантирует его. Делая первый шаг, игрок не должен путать «повышение шансов» и «гарантированный выигрыш».
Второй шаг еще сложнее: построить и применить статистическую модель задачи. Цепочка рассуждений может быть такой.
Сначала игрок делает выбор одной из трех дверей. По условию приз размещен за любой из них с одинаковой вероятностью. На первом шаге вероятность выбора приза равна 1/3. На рисунке ниже изображено дерево решений после первоначального выбора игрока. Дверь, за которой приз, закрашена:
Дальше ведущий открывает одну из дверей, не выбранных игроком. Игроку кажется, что ведущий выбирает дверь, которую открыть. Однако, это не всегда так. Поведение ведущего обусловлено первым выбором игрока:
Вероятность того, что приз за дверью, которую ведущий оставил закрытой, рассчитывается по формуле условной вероятности. И эти вероятности различаются для разных исходов, как показывает дерево решений. Закрытые двери, за которыми приз, закрашены:
Игрок суммирует вероятности по каждой стратегии и получает их статистическую оценку. На рисунке видно, что вероятность выигрыша при смене двери (стратегия «switch») в два раза выше:
После того, как стратегии оценены, игрок должен отказаться от первоначального выбора. Это сложно само по себе. Игрок будет стремится сохранить первоначальный выбор, так как это проще. Например, потенциальный покупатель гораздо вероятнее не будет отключать по умолчанию включенную услугу, нежели включит ее. В общем случае это приводит к систематическому отклонению поведения игроков от рационального.
Трудности применения статистического мышления
Проблемы, связанные с применением статистического мышления и рационального мышления вообще рассматриваются в книге Дэвида Канемана «Думай медленно, решай быстро». Исследования Канемана и его коллег показали, что человек склонен ошибаться в ситуациях, если нужно провести даже простые математические расчеты, не говоря уже об оценке вероятности.
Канеман вводит понятие двух систем. Система 1 это «быстрое», интуитивное, эвристическое мышление. Им человек пользуется, например, для определения настроения по выражению лица или при оценке дорожной ситуации, когда ведет автомобиль. Система 1 это автоматическая, почти мгновенная реакция, и работает в большинстве повседневных ситуаций.
Система 2 — «медленное», рациональное, математическое и статистическое мышление. Эта система подключается с усилием. Человек должен осознать, что автоматическое решение неправильное, задуматься и провести расчеты.
Ключевая проблема заключается в том, что в ситуации, где требуется подумать, человек полагается на автоматическое решение, предлагаемое системой 1. А эта система делает выводы, в первую очередь, на основании похожести вариантов. В парадоксе Монти Холла, после того, как ведущий открыл одну из дверей, две оставшихся выглядят одинаково, а обусловленное поведение ведущего старательно замаскировано. Ситуация представляется симметричной, а вероятности одинаковыми. Системе 1 не за что зацепиться, чтобы заметить вероятностную асимметрию. А системе 2 некогда подключиться. Тем более, что ведущий разными способами старается сбить игрока с толку.
Система 1 тренируется на многократном повторении ситуаций, доводя выбор до автоматизма (распознавание лиц, вождение автомобиля). Человек видит похожую ситуацию, что-то, что ему знакомо, и делает выбор, который ранее был успешен в аналогичных ситуациях.
Система 2 подразумевает, что человек начинает анализировать ситуацию, чтобы принять решение. В случае со статистическими задачами правильный ответ не очевиден. Чтобы к нему прийти, человек должен проанализировать данные, произвести расчеты и выбрать наибольшие значения статистических показателей.
Общее между интуицией и статистикой
Основная идея Дэвида Канемана в том, что система 1 (интуитивная) и система 2 (рациональная) различаются. В общем случае так и есть, однако, применительно к статистике между ними есть сходство.
Предположим, что все участники шоу Монти Холла собрались, чтобы обсудить результаты участия в шоу. Собравшиеся разбились на две группы: тех, кто остался с первоначально выбранной дверью и тех, кто поменял дверь. Согласно статистике, подсчет участников и их результатов покажет, что те участники, которые меняли дверь, выигрывали чаще. Если участников в обеих группах много, то доля победителей в группе сменивших дверь, будет примерно в два раза выше, чем в другой.
Достаточное количество участников, при котором будет видна статистическая закономерность, определяется законом больших чисел. Чем больше игроков примет участие в собрании, тем более результаты подсчетов их успехов и неудач будут соответствовать теоретическим. Другими словами, статистика начинает работать, когда игра была повторена разными участниками много раз. Если бы такое сообщество игроков существовало, то со временем они бы пришли к правильной стратегии.
Таким образом, в статистических расчетах система 2 опирается на закон больших чисел — достаточно большое (в идеале бесконечное) количество испытаний. Но и системе 1 большое количество испытаний позволяет принимать правильные решения. Многократное повторение доводит ту или иную способность человека до автоматизма.
Правила для двух систем:
Можно сказать, что расчет вероятности отражает коллективный опыт всех реальных и возможных участников игры Монти Холла. Для ситуаций индивидуального выбора стратегий статистика выступает как коллективная интуиция. Остается сделать статистику наглядной при помощи подходящей визуализации.
Диаграмма-шкала для визуализации теоретической и частотной вероятности
На примере парадокса Монти Холла мы смоделировали выбор человеком правильной стратегии с привлечением статистических расчетов. В общем случае:
Если поставить задачу помочь выиграть игроку, а не сбить его с толку, как на шоу, то в визуализации данных или пользовательском интерфейсе можно дополнить «двери», между которыми выбирает «игрок», диаграммами-шкалами. На такой диаграмме шкала задает градации изменения величины, и на шкалу накладывается столбик фактического значения по аналогии с термометром.
На диаграмме-шкале удобно совместить теоретическое, ожидаемое количество выигрышей (выделено серым) и фактическое после всех предыдущих игр (узкий черный столбик). Фактическое значение меняется после каждого принятого решения по выбору одной из двух стратегий и сохраняется на протяжении всей серии игр:
Таким образом, подходящая визуализация статистических данных помогает человеку выбрать правильную стратегию. Например, в интерфейсе, похожем на прототип, элемент интерфейса, соответствующий стратегии, может быть помечен статистическим виджетом, похожим на диаграмму-шкалу. Изображение фактических данных полезно, если пользователь выбирает между примерно одинаково успешными стратегиями. Оно позволяет ему быстро прийти к заключению:
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Представьте, что некий банкир предлагает вам выбрать одну из трёх закрытых коробочек. В одной из них 50 центов, в другой – один доллар, в третьей – 10 тысяч долларов. Какую выберете, та вам и достанется в качестве приза.
Вы выбираете наугад, скажем, коробочку №1. И тут банкир (который, естественно, знает, где что) прямо на ваших глазах открывает коробочку с одним долларом (допустим, это №2), после чего предлагает вам поменять изначально выбранную коробочку №1 на коробочку №3.
Стоит ли вам менять своё решение? Увеличатся ли при этом ваши шансы получить 10 тысяч?
Это и есть парадокс Монти Холла — задача теории вероятности, решение которой, на первый взгляд, противоречит здравому смыслу. Над этой задачей люди ломают головы с 1975 года.
Парадокс получил название в честь ведущего популярного американского телешоу «Let’s Make a Deal». В этом телешоу были похожие правила, только участники выбирали двери, за двумя из которых прятались козы, за третьей – Кадиллак.
Большинство игроков рассуждали, что после того, как закрытых дверей осталось две и за одной из них находится Кадиллак, то шансы его получить 50-50.Очевидно, что когда ведущий открывает одну дверь и предлагает вам поменять своё решение, он начинает новую игру. Поменяете вы решение или не поменяете, ваши шансы всё равно будут равны 50 процентам. Так ведь?
Оказывается, что нет. На самом деле, поменяв решение, вы удвоите шансы на успех. Почему?
Наиболее простое объяснение этого ответа состоит в следующем соображении. Для того, чтобы выиграть автомобиль без изменения выбора, игрок должен сразу угадать дверь, за которой стоит автомобиль. Вероятность этого равна 1/3. Если же игрок первоначально попадает на дверь, за которой стоит коза (а вероятность этого события 2/3, поскольку есть две козы и лишь один автомобиль), то он может однозначно выиграть автомобиль, изменив своё решение, так как остаются автомобиль и одна коза, а дверь с козой ведущий уже открыл.
Таким образом, без смены выбора игрок остаётся при своей первоначальной вероятности выигрыша 1/3, а при смене первоначального выбора, игрок оборачивает себе на пользу в два раза большую оставшуюся вероятность того, что в начале он не угадал.
Также интуитивно понятное объяснение можно сделать, поменяв местами два события. Первое событие — принятие решения игроком о смене двери, второе событие — открытие лишней двери. Это допустимо, так как открытие лишней двери не дает игроку никакой новой информации (док-во см. в этой статье). Тогда задачу можно свести к следующей формулировке. В первый момент времени игрок делит двери на две группы: в первой группе одна дверь (та что он выбрал), во второй группе две оставшиеся двери. В следующий момент времени игрок делает выбор между группами. Очевидно, что для первой группы вероятность выигрыша 1/3, для второй группы 2/3. Игрок выбирает вторую группу. Во второй группе он может открыть обе двери. Одну открывает ведущий, а вторую сам игрок.
Попробуем дать «самое понятное» объяснение. Переформулируем задачу: Честный ведущий объявляет игроку, что за одной из трех дверей — автомобиль, и предлагает ему сначала указать на одну из дверей, а после этого выбрать одно из двух действий: открыть указанную дверь (в старой формулировке это называется «не изменять своего выбора») или открыть две другие (в старой формулировке это как раз и будет «изменить выбор». Подумайте, здесь и заключен ключ к пониманию!). Ясно, что игрок выберет второе из двух действий, так как вероятность получения автомобиля в этом случае в два раза выше. А та мелочь, что ведущий ещё до выбора действия «показал козу», никак не помогает и не мешает выбору, ведь за одной из двух дверей всегда найдется коза и ведущий обязательно её покажет при любом ходе игры, так что игрок может на эту козу и не смотреть. Дело игрока, если он выбрал второе действие — сказать «спасибо» ведущему за то, что он избавил его от труда самому открывать одну из двух дверей, и открыть другую. Ну, или ещё проще. Представим себе эту ситуацию с точки зрения ведущего, который проделывает подобную процедуру с десятками игроков. Поскольку он прекрасно знает, что находится за дверями, то, в среднем, в двух случаях из трёх, он заранее видит, что игрок выбрал «не ту» дверь. Поэтому уж для него точно нет никакого парадокса в том, что, правильная стратегия состоит в изменении выбора после открытия первой двери: ведь тогда в тех же двух случаях из трёх игрок будет уезжать со студии на новой машине.
Наконец, самое «наивное» доказательство. Пусть тот, кто стоит на своем выборе, называется «Упрямым», а тот, кто следует указаниям ведущего, зовется «Внимательным». Тогда Упрямый выигрывает, если он изначально угадал автомобиль (1/3), а Внимательный — если он вначале промахнулся и попал на козу (2/3). Ведь только в этом случае он потом укажет на дверь с автомобилем.
Монти Холл, продюсер и ведущий шоу Let’s Make a Deal с 1963-го по 1991 год.
В 1990 году эта задача и её решение были опубликованы в американском журнале “Parade”. Публикация вызвала шквал возмущённых отзывов читателей, многие из которых обладали научными степенями.
Главная претензия заключалась в том, что не все условия задачи были оговорены, и любой нюанс мог повлиять на результат. Например, ведущий мог предложить поменять решение только в том случае, если игрок первым ходом выбрал автомобиль. Очевидно, что смена первоначального выбора в такой ситуации приведёт к гарантированному проигрышу.
Однако за всё время существования телешоу Монти Холла люди, менявшие решение, действительно выигрывали вдвое чаще:
Из 30 игроков, поменявших первоначальное решение, Кадиллак выиграли 18 – то есть 60%
Из 30 игроков, которые остались при своём выборе, Кадиллак выиграли 11 – то есть примерно 36%
Так что приведённые в решении рассуждения, какими бы нелогичными они не казались, подтверждаются практикой.
Увеличение количества дверей
Для того, чтобы легче понять суть происходящего, можно рассмотреть случай, когда игрок видит перед собой не три двери, а, например, сто. При этом за одной из дверей находится автомобиль, а за остальными 99 — козы. Игрок выбирает одну из дверей, при этом в 99 % случаев он выберет дверь с козой, а шансы сразу выбрать дверь с автомобилем очень малы — они составляют 1 %. После этого ведущий открывает 98 дверей с козами и предлагает игроку выбрать оставшуюся дверь. При этом в 99 % случаев автомобиль будет находиться за этой оставшейся дверью, поскольку шансы на то, что игрок сразу выбрал правильную дверь, очень малы. Понятно, что в этой ситуации рационально мыслящий игрок должен всегда принимать предложение ведущего.
Следует отметить, что в случае множества дверей, даже если ведущий будет оставлять закрытой не одну дверь, а несколько, и предлагать игроку выбрать одну из них, то при смене первоначального выбора шансы игрока выиграть автомобиль всё равно будут увеличиваться, хотя и не столь значительно. Например, рассмотрим ситуацию, когда игрок выбирает одну дверь из ста, и затем ведущий открывает только одну дверь из оставшихся, предлагая игроку изменить свой выбор. При этом шансы на то, что автомобиль находится за первоначально выбранной игроком дверью, остаются прежними — 1/100, а для остальных дверей шансы изменяются: суммарная вероятность того, что автомобиль находится за одной из оставшихся дверей (99/100) распределяется теперь не на 99 дверей, а на 98. Поэтому вероятность нахождения автомобиля за каждой из этих дверей будет равна не 1/100, а 99/9800. Прирост вероятности составит примерно 1 %.
Дерево возможных решений игрока и ведущего, показывающее вероятность каждого исхода Более формально сценарий игры может быть описан c помощью дерева принятия решений. В первых двух случаях, когда игрок сначала выбрал дверь, за которой находится коза, изменение выбора приводит к выигрышу. В двух последних случаях, когда игрок сначала выбрал дверь с автомобилем, изменение выбора приводит к проигрышу.
Если же вам непонятно все равно, плюньте на формулы и просто проверьте всё статистически. Еще один вариант объяснения:
Всё ещё не верите? Предположим, что вы выбрали дверь №1. Здесь представлены все возможные варианты того, что может произойти в этом случае:
Если вы оставляете свой первоначальный выбор, вы выигрываете один раз из трёх; если меняете выбор – угадываете два раза из трёх.
Вы по-прежнему не уверены? Давайте проделаем то же самое, только с 50 дверями. Вы выбираете дверь №1.
А мы открываем остальные 48 дверей, за которыми спрятаны козлы. Вы ещё уверены в своём выборе? Помните, что у вас есть 1 шанс из 50 угадать нужную вам дверь с первой попытки. Здесь действует тот же самый принцип.
Конечно, игра подразумевает, что вы непременно хотели выиграть автомобиль, а не козла.
Такая вот занимательная математика.











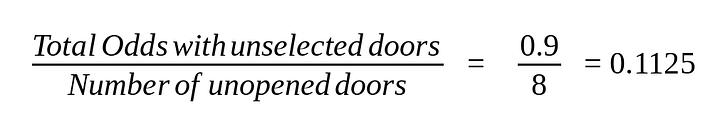

 masterok
masterok