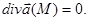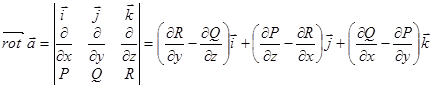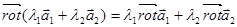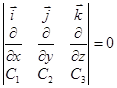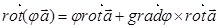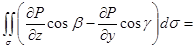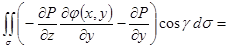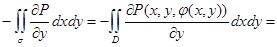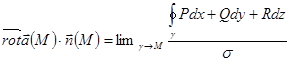определение дивергенции соленоидальное поле
Определение соленоидального поля



Соленоидальные поля
Векторное поле a называется соленоидальным, если в каждой его точке дивергенция равна нулю:
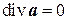
В связи с этим соленоидальные поля часто называют несжимаемым. Происхождение этого названия легко понять, если обратится к гидродинамическому смыслу дивергенции. Простейшим примером соленоидального поля является поле скоростей несжимаемой жидкости или магнитное поле.
Мы выяснили, что div rot jº0. Это значит, что если векторное поле является соленоидальным, то его можно представить в виде ротора некоторого поля A:
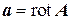
Вектор A называется векторным потенциалом данного поля. Отметим, что условие (8.28) необходимо, но, вообще говоря, не достаточно для существования векторного потенциала.
Поток соленоидального поля через любою замкнутую поверхность, целиком лежащей в области непрерывности поля, равен нулю:
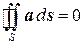
Эта формула является следствием теоремы Остроградского-Гаусса. Однако теорему Остроградского-Гаусса можно применить только для односвязных областей, т.е. только для поверхностей, которые можно стянуть в точку поля, не выходя за пределы поля.
Итак, векторное поле является соленоидальным тогда и только тогда, когда равен нулю поток через любою замкнутую поверхность, которую можно стянуть в точку, не пересекая его границ.
Отметим, что выполнение любого из условий (8.27)-(8.29) являются достаточными для того, чтобы векторное поле было соленоидальным, и выполнялись остальные условия.
О понимании, вычислении и измерении дивергенции векторных полей физических величин
А. С. Чуев.
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Московский государственный технический университет имени Н. Э. Баумана» Национальный исследовательский университет техники и технологий (МГТУ им. Н. Э. Баумана),
Россия, Москва, e-mail: chuev@mail.ru
Ключевые слова: физические поля, дивергенция, теория поля, электрическое поле, магнитное поле, намагниченность.
Key words: physical fields, divergence, field theory, the electric field, magnetic field, the magnetization.
Понятие «дивергенция» переводится на русский язык как расходимость (можно к этому отнести и сходимость) линий векторного поля. Логически это понятно, в пространственно расходящемся или сходящемся векторном потоке обязательно есть изменение плотности линий поля, что возможно (при сохраняющейся величине потока) только за счет изменения модуля вектора, посему дивергенция (расходимость) неотделима от изменений модуля вектора. В однородном векторном поле дивергенция, согласно своему понятию, должна быть равна нулю.
Несмотря на сказанное, в математической теории поля и полевой физике дивергенция считается, чаще всего, ненулевой только в истоках и стоках поля, при этом числовое значение дивергенции в них, как правило, неопределимо по причине неопределенности их размеров. Например, для центральных полей типа электрического и гравитационного дивергенция считается равной нулю всюду кроме истоков и стоков. Если же брать в качестве примера магнитное поле, то равенство нулю дивергенции вектора магнитной индукции В принято безусловным и возведено в закон (четвертое уравнение Максвелла).
Хорошо известны изображения пространственно неоднородных полей в виде расходящихся и сходящихся силовых линий полей центрального типа (рис.1) и соленоидального поля стержневого магнита (рис.2). Силовые линии поля строятся по касательным, определяющим направление силы в любой точке пространства, окружающего электрический заряд или магнит.
Густота линий поля определяет числовое значение полевого вектора в любой точке поля. Сам вектор касателен к линии поля, проходящей через данную точку, а его направление определяется действующим соглашением о положительной направленности.
Пространственная расходимость и сходимость линий поля, создаваемых электрическими зарядами очевидна, потому как густота линий убывает при отдалении от центра, указывая на ослабление поля при отдалении от источника или стока поля. Однако в математической теории поля и в большинстве физических толкований 3 дивергенция векторных полей центрального типа (рис. 1) всюду вне источника и стока считается равной нулю.
Приводимая на рис. 2 картина силовых линий магнитного поля тоже наглядно иллюстрирует, что данное поле неоднородно. Густота силовых линий магнитного поля, определяющих величину и направление силового вектора В, вблизи торцов магнита самая большая, а в отдалении от торцов магнита становится значительно меньше. На бесконечно большом удалении от магнита значение магнитной индукции будет нулевым. Однако в соответствии с четвертым уравнением Максвелла дивергенция вектора магнитной индукции В принимается всюду равной нулю. Считается также, что источников и стоков у магнитного поля нет, а линии поля замкнуты сами на себя.
Приведем несколько примеров из учебников с имеющейся там трактовкой понятия дивергенции. Возьмем классический учебник И. Е. Тамма «Основы теории электричества» [1, стр.586]. Тамм пишет: «Отметим в заключение, что в гидродинамике дивергенция скорости жидкости v имеет непосредственное физическое значение. Действительно, в каждой точке жидкости
равна рассчитанному на единицу объема количеству жидкости, вытекающей из элемента объема dV, окружающего рассматриваемую точку».
Другой источник [2, стр.24], описывая дивергенцию статического электрического поля, излагает так: «В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда р в этой точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле Е отличается друг от друга. Это же относится, вообще говоря,и к пространственным производным ∂Ех/∂х, ∂Еу/∂у, ∂Ez/∂z. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю».
В последней фразе чувствуются сильные нотки сомнения в правильности излагаемого, но они прикрыты ссылкой на авторитет теоремы Гаусса. Действительно, трудно объяснить положение, согласно которому производные по координатам есть, но их сумма всегда равна нулю. Это явно не соответствует элементарной логике. Ведь координатные проекции изменяющегося вектора вполне могут быть одного знака, а изменение вектора может быть и вовсе только по одной координате.
Математически дивергенция выражается не только формулой (1), но и как функция пространственной производной вектора, обозначаемая оператором набла [4, стр. 3581]:
Таким образом, формула (2) выражает не совсем привычное на первый взгляд, но истинное представление, соответствующее своему понятию-дивергенции векторного поля, как скорости изменения вектора в любой точке поля в своем собственном направлении, то есть по модулю.
Подтверждение такому (или примерно такому) пониманию дивергенции можно обнаружить в других источниках. В учебнике по математике [4, стр.359] встречается такая фраза: «. всякое векторное поле А дает некоторое скалярное поле divA, а именно поле своей расходимости». Другой источник [5, стр.402]: «Дивергенция div a векторного поля а в точке М есть скаляр (действительное число). Рассматривая дивергенцию в каждой точке области определения векторного поля а, мы получаем скалярное поле div а».
Понимание ошибочности привязки понятия дивергенции лишь к истокам и стокам векторного поля в физике зреет уже давно. Осознание этого уже появилось в гидродинамике [6]. По мнению автора не за горами признание аналогичного положения и в других областях физики, в частности в электростатике и магнитостатике.
Попытку вывести понятие дивергенции из «прокрустова ложа» истоков и стоков можно обнаружить в источнике [7, стр.171]. Там приводится такая формула:
В формуле (4) нет устремления объема в точку, а анализируются внешняя поверхность и объем, которым принадлежит рассматриваемая точка поля. При правильной интерпретации этой формулы и применительно к векторным полям центрального типа она дает достаточно верный результат оценки величины дивергенции векторного поля.
В источнике [8] для дивергенции приводится еще одна отличная от выражения (1) Формула:
Здесь дивергенция определяется как объемная плотность потока векторной величины в той или иной точке пространства векторного поля. Считается [8], что такое определение дивергенции применимо не только к декартовым системам координат. В чем-то аналогичный подход обнаруживается и в работе [9, стр.22]: «. дивергенция векторного поля а (М) является объемной плотностью потока векторного поля а (М) в данной точке М».
Однако, если векторное поле однородное, то объемная плотность потока векторного поля будет иметь одно определенное для всех точек поля значение, а расходимости (надо понимать, дивергенции) линий поля не будет. Налицо противоречие. В наглядных примерах по рис.1 и рис.2 видно, что дивергенция (расходимость) электрических и магнитных силовых линий определяется неоднородностью поля, которое связано с изменением модуля вектора, такое значение определяется плотностью потока линий поля, зависящей от пространственного удаления рассматриваемой точки от источника или стока поля. В однородном векторном поле дивергенции (расходимости) нет и быть не может.
По мнению автора, дивергенция, по сути своей, должна быть не плотностью потока векторного поля, что присуще и однородным векторным полям, а скоростью пространственного изменения плотности потока вектора в той или иной точке поля, которое по идее должно совпадать с пространственной производной вектора по формуле (2). Математически это можно выразить так:
где 
Для сравнения приведем в табличном формате различные варианты определения и понимания (толкования) дивергенции, в том числе отстаиваемые автором в настоящей работе (см. таблицу 1).
Приведем расчетные оценки дивергенции для различных вариантов ее определения по таблице 1, применительно к вектору D электростатического поля в точке М, находящейся на расстоянии г от центрального заряда q0.
А. Общепринятое значение дивергенции вне истоков и стоков поля равно нулю (div D = 0).
Б. Значение, вычисленное из условия равномерной объемной плотности заряда, приходящегося на весь рассматриваемый сферический объем, что можно понимать как своеобразное (грубое) определение дивергенции для полей центрального типа, составляет:
В. Авторские варианты определения дивергенции по вариантам 1 и 2 по модулю должны быть эквивалентны. Значение дивергенции по варианту 1:
По варианту 2, если принимать дивергенцию у расходящихся полей положительной:
В расчетах магнитных цепей обычно дополнительно используют еще одну физическую величину напряженность магнитного поля Н, хотя в действительности она применима лишь к токовым источникам магнитного поля, а не к источникам поля в виде постоянных магнитов. Этот вопрос более подробно рассмотрен в авторской работе [11].
Расчетное определение дивергенции магнитного поля, создаваемого стержневым магнитом типа, изображенного на рис. 2, возможно двумя путями. В первом варианте следует принимать неизменным поток магнитной индукции 0=B‘S, выходящий из торца магнита и расходящийся в окружающем пространстве. Тогда изменение модуля магнитной индукции будет обратно пропорционально увеличению площади потока. Изменение площади потока вне постоянных магнитов можно определить известным эмпирическим методом с использованием железных опилок.
Второй вариант расчета основан на принятии неизменным модуля суммарного магнитного дипольного момента, создаваемого молекулами и атомами магнита. В этом случае дивергенцию рассчитывают как уменьшение модуля векторов магнитной индукции и намагниченности в окружающем магнит пространстве, исходя из условия увеличения объема пространства, приходящегося на суммарный магнитный дипольный момент тела магнита. В расчетах магнитных систем с малыми воздушными зазорами этот вариант расчета (из приведенных двух) будет единственно возможным и он дает верный результат. Близкий к этому подход, правда, с энергетических позиций и с некорректным, по мнению автора, использованием напряженности магнитного поля Н, описан в работе [12, стр.457].
Теперь рассмотрим возможность опытного измерения дивергенции, что должно поставить завершающую точку в теоретических разногласиях математиков и физиков об этом параметре.
Для статического электрического поля проблема опытного измерения дивергенции решается достаточно просто. Измеряем напряженность поля в двух точках, лежащих на линии поля в окрестности точки, в которой определяется дивергенция. Разницу полученных измерений делим на расстояние между точками измерений, это и будет средним значением дивергенции вектора Е для искомой точки поля. Дивергенция «материального» [12] вектора D, который чуть выше фигурировал в расчетах, определяется по этим измерениям с учетом электрической постоянной £0 и относительной диэлектрической проницаемости среды.
Для статического магнитного поля практическое измерение дивергенции выполняется подобным же образом, правда определять линии поля здесь несколько сложнее, потому как оно не центральное. Кроме того, следует учитывать, что измеряя значение полевого параметра магнитной индукции В, мы фактически измеряем намагниченность вакуума ]0. В работах [13,14] показано, что вектор В относится к чисто полевым (по мнению автора, фантомным) величинам, которые модельного (материального) представления не имеют, хотя вроде бы на практике и измеримы. На самом деле измерение магнитной индукции В сводится к измерению разности электрических потенциалов (в датчиках Холла) или электродвижущей силы, образуемой при изменении (во времени) магнитного потока Ф, который выражаем и через другие магнитные величины. Покажем это в формулах.
Вне магнита индукция В связана с намагниченностью среды соотношением
В воздухе μ=1, поэтому максимальная величина магнитного потока определяется произведением площади S измерительной рамки на магнитную постоянную μ0 и на вектор намагниченности вакуума J0 который не вполне оправданно (при отсутствии токов проводимости) считают вектором напряженности магнитного поля Н. Алгебраическое соотношение названных величин имеет вид:
При фиксированной величине площади S измерительной рамки и ее ориентации перпендикулярно измеряемому полю пространственные изменения магнитного потока будут соответствовать соответствующим изменениям намагниченности окружающего магнит пространства. По этим измерениям можно определить дивергенцию векторов В и Jo в интересующей нас точке поля.
ВЫВОДЫ
2. Для полей центрального типа дивергенцию в каждой точке поля можно грубо вычислять как объемную плотность источника поля (заряда или массы) в сферическом объеме, на поверхности которого расположена рассматриваемая точка. Более точно дивергенция вычисляется как пространственное изменение плотности потока векторного поля. В такой форме дивергенция вычислима для полей любого типа и формы.
1. Тамм И.Е. Основы теории электричества. Учеб. Пособие для вузов,- 11-е изд., испр. и доп.- М.: Физматлит-2003.- 616 с.
3. Парселл Э. Электричество и магнетизм: Учебное руководство; Пер с англ./Под ред. А. Н. Школьникова и А. О. Вайсберга- 3-е изд., испр-М.: Наука-1983- (Берклеевский курс физики).- 410 с.
6. Волков П. К. О природе движения жидкости. /Вестник Югорского государственного университета-2011.- Выпуск 2 (21).- С. 8-28.
7. Справочник по математике (для научных работников и инженеров). Корн Г., Корн Т.- М.: НАУКА,- 1973,- 832 с.
10. Ильин В. А., Садовничий В. А., Сендов Бл. X. Математический анализ. Продолжение курса. Под ред. А. Н. Тихонова- М.: Изд. МГУ.- 1987.- 358 с.
12. Боровик Е. С., Еременко В. В., Мильнер А. С. Лекции по магнетизму- 3-е изд. перераб. и доп.-М.: ФИЗМАТЛИТ,- 2005.- 512 с.
Определение дивергенции соленоидальное поле
Поле 
Соленоидальиое поле называют также несжимаемым. Происхождение последнего названия достаточно понятно в связи с гидромеханическим смыслом дивергенции. Простейшим примером несжимаемого поля является поле скоростей потока несжимаемой жидкости. Причина названия такого поля трубчатым (солепоидальным) выяснится дальше.
2. Поле ротации.
Рассмотрим поле ротации произвольного векторного поля Р:
Вычислим дивергенцию этого поля:
Теорема. Поле ротации произвольного векторного поля является соленоидальным, т. е.
Замечание. Чрезвычайно наглядно это утверждение выглядит в операторной форме:
Но мы знаем, что векторно-скалярное произведение, содержащее два одинаковых множителя, равно нулю. Поэтому
Соленоидальное поле и его свойства.
Векторное поле 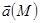
Свойства соленоидального поля.
1) Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.
Необходимость следует из формулы Остроградского – Гаусса, достаточность – из инвариантного определения дивергенции.
2) Поток соленоидального поля через любую поверхность, окружающую изолированный источник или сток, один и тот же.

| Рассмотрим две замкнутых поверхности 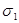 и и 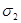 , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям. Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости. В той и другой области поле соленоидально. Следовательно, , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям. Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости. В той и другой области поле соленоидально. Следовательно, |
поток векторного поля через границы этих областей равен нулю.
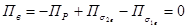
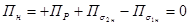
Складывая эти выражения, получим 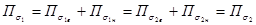
3) Поток соленоидального поля через произвольное сечение векторной трубки один и тот же.
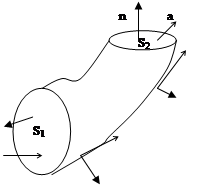 | Обозначим Sбок –боковую поверхность векторной трубки. На боковой поверхности направления нормали и векторного поля ортогональны, так как векторная трубка образована векторными линиями, а вектор поля направлен по касательной к векторной линии. Поэтому поток векторного поля через боковую поверхность векторной трубки равен нулю (ПSбок.= 0). Учитывая направления нормалей и вектора поля на сечениях векторной трубки S1 и S2, а также соленодальность поля, получим 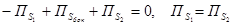 . . |
Следствие. Векторные линии соленоидального поля не могут начинаться и заканчиваться внутри поля.
В самом деле, иначе конечный поток приходился бы на нулевую площадь источника или стока, что требовало бы бесконечной мощности источника или стока.
Лекция 9 Формула Стокса.
Ротор векторного поля.
Назовем ротором векторного поля 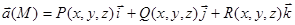
Свойства ротора.
1) Линейность
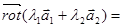
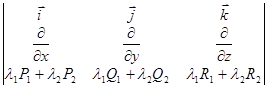
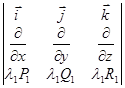
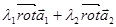
2) 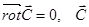
3)

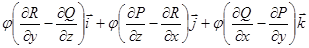
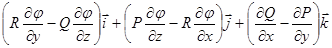
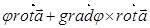
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность 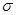
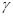
Пусть компоненты векторного поля 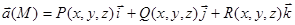
Тогда справедлива формула Стокса
Замечание. Нормаль к поверхности 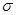
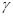
Доказательство теоремы Стокса.
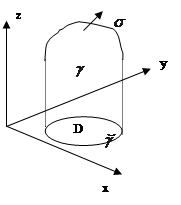  | Как и формула Остроградского – Гаусса, формула Стокса состоит из трех независимых частей (в силу произвольности компонент векторного поля). Докажем одну из этих частей, остальные формулы доказываются аналогично. Докажем 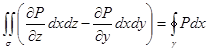 — часть формулы Стокса, в которой содержится только компонента P. Предположим, что поверхность — часть формулы Стокса, в которой содержится только компонента P. Предположим, что поверхность 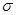 описывается уравнением описывается уравнением 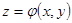 . Тогда нормаль к поверхности . Тогда нормаль к поверхности |
представляет собой вектор
Отсюда видно, что 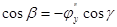
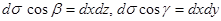

(на поверхности 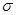
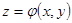
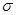
=
Используем формулу Грина для области D с ее границей 

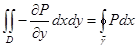
= 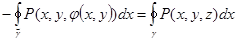
В самом деле, на контуре 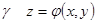

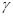
Одна из частей формулы Стокса доказана.
Линейным интеграломвекторного поля 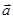
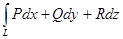
Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляциейвекторного поля называется линейный интеграл по замкнутому контуру.
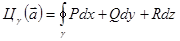
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
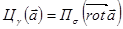
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора.
Рассмотрим произвольную точку M в области V. Проведем через нее поверхность 
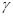
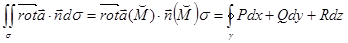
Здесь, как и ранее 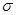
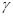
Это и есть инвариантное определение ротора.
Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором 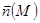
Если направление 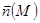
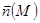
Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая.
Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью
Векторное поле линейной скорости 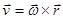
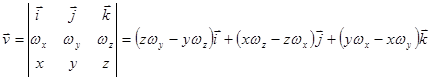
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.















.jpg)
.jpg)