однородное поле силы тяжести

Силовая функция однородного поля силы тяжести

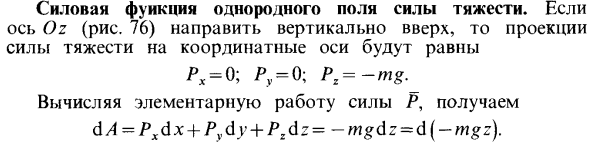
Силовая функция однородного поля силы тяжести

Эти пары сил получаются из пар сил, произвольно расположенных в плоскости пересечения путем перемещения, вращения и одновременной смены плеч и сил в рабочей плоскости. Людмила Фирмаль

Уравнение (83) определяет силовую функцию однородного гравитационного поля, то есть поля, где сила тяжести постоянна по абсолютной величине и направлению. Уравнение для горизонтальной плоскости U = C или z = const. Другими словами, горизонтальная плоскость является горизонтальной плоскостью.

Если крутящий момент относительно выбранной точки на действующей поверхности силы выбирается в действующей поверхности силовой пары как частный случай, то алгебраическая сумма момента силовой пары: векторного момента силовой пары задается разрезом.

Итак, если вы добавите две пары сил на плоскости, которые пересекаются, вы получите эквивалентную пару сил. Людмила Фирмаль

В этом случае векторные моменты параллельны, и поэтому векторное сложение переходит в алгебру, поэтому сложение пар сил, находящихся в одной плоскости или параллельной плоскости, не обязательно для пересечения.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Однородное поле силы тяжести

Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения : две любые материальные точки массами m 1 и m 2 притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:

Земля не является «материальной точкой» для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.

В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная

Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:

1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести ( ) в лифте вертикально вниз;

Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

1. Напряженность гравитационного поля ( ), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):

Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ( )

Единица измерения [φ]=Дж/кг.

Потенциальная энергия тела в гравитационном поле равна:

Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ 1 в точку с потенциалом φ 2 равна:

Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.

В качестве примера рассмотрим гравитационное поле материальной точки.

Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).

Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:

Потенциальная энергия тела на высоте h над поверхностью Земли, равна:

Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.

Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна

Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.

Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:

На Земле приблизительно инерциальными являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно точек на поверхности Земли.

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, рассматривают три варианта проявления этих сил.

1. Сила инерции возникает при ускоренном поступательном движении системы отсчета и направлена против вектора ускорения неинерциальной системы отсчета :

Действию центробежной силы инерции подвергаются пассажиры в движущемся транспорте на поворотах; летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов) принимаются специальные меры для уравновешивания центробежных сил инерции.

равна произведению удвоенной массы тела на векторное произведение скорости поступательного движения тела относительно системы отсчета и угловой скорости вращения системы отсчета. Эта сила направлена перпендикулярно векторам скорости тела и угловой скорости вращения системы в соответствии с правилом правого винта.

Земля представляет собой вращающуюся систему отсчета и действие силы Кориолиса объясняет ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис.1.8.4), то сила Кориолиса будет направлена вправо по отношению к направлению движения, и тело отклонится на восток. Если тело движется в юг, то сила Кориолиса также направлена вправо по отношению к направлению движения, и тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к направлению движения.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета : произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции):

Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета, поэтому они не подчиняются третьему закону Ньютона. Два основных положения механики: 1) ускорение всегда вызывается силой; 2) сила всегда обусловлена взаимодействием между телами, в неинерциальных системах отсчета одновременно не выполняются.

Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах отсчета таких сил не существует.

Все тела независимо от их масс и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета.

Силы инерции, действующие на тела неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия.

Все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести.

Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции.

Принципа эквивалентности Эйнштейна: все физические явления в поле сил тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.

Принцип эквивалентности гравитационных сил и сил инерции можно рассматривать как принцип эквивалентности гравитационной и инерционной масс тела.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013

Источник

§ 18. Силовое поле. Центр тяжести твердого тела

Область, в каждой точке которой на помещенную туда материальную частицу действует сила, зависящая от координат этой точки, называется силовым полем.

Например, на каждую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила тяжести. Эти силы образуют поле сил тяжести. Силы тяжести, действующие на частицы тела, можно считать параллельными друг другу и сохраняющими для каждой частицы постоянное значение при любых поворотах тела. Поле тяжести, в котором выполняются эти два условия, называют однородным полем тяжести.

Равнодействующую сил тяжести , ,…, действующих на частицы тела, обозначим через (рис. 39). Модуль этой силы называется весом тела и определяется равенством

. (41)

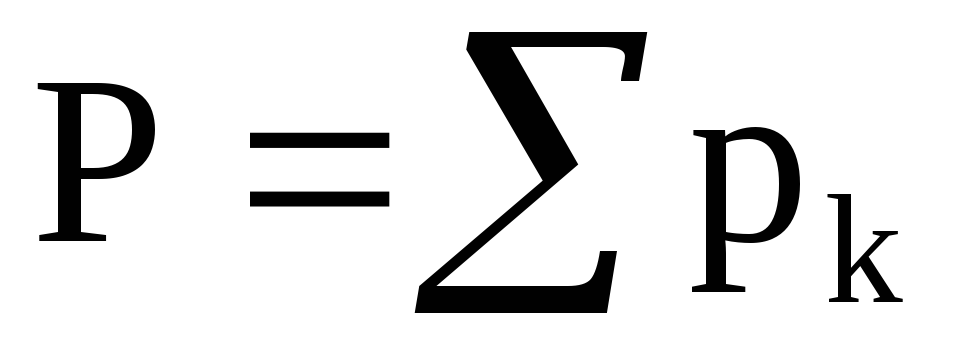
При повороте тела силы остаются параллельными друг другу. Следовательно, равнодействующая сил будет при любых положениях тела проходить через одну и ту же точку С, являющуюся центром параллельных сил тяжести . Эта точка называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей сил тяжести, действующих на частицы тела, при любом положении тела в пространстве.

Координаты центра тяжести, как центра параллельных сил, определяются формулами (40); следовательно,

, ,, (42)

где x_k,y_k,z_k – координаты точек приложения сил тяжести .

Отметим, что центр тяжести – это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).

§19. Координаты центров тяжести однородных тел

Для однородного тела вес p_k любой его части и вес Р всего тела пропорциональны соответственно объемам v_k этой части и V всего тела, т.е.

, ,

где – вес единицы объема.

Подставив эти значения Р и р_k в формулы (42), получим

, ,. (43)

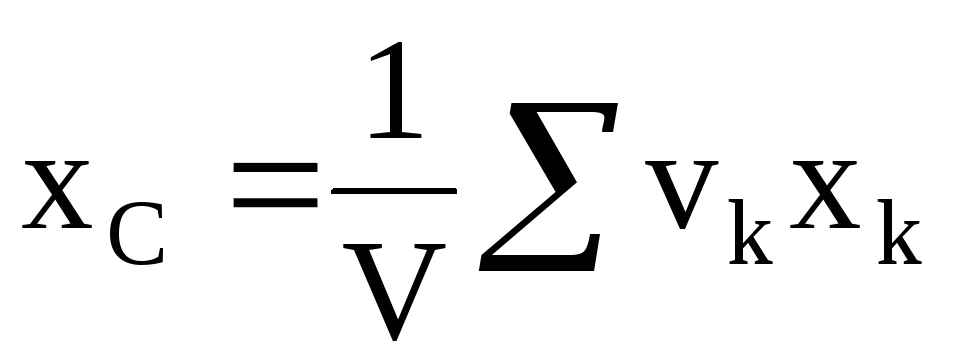
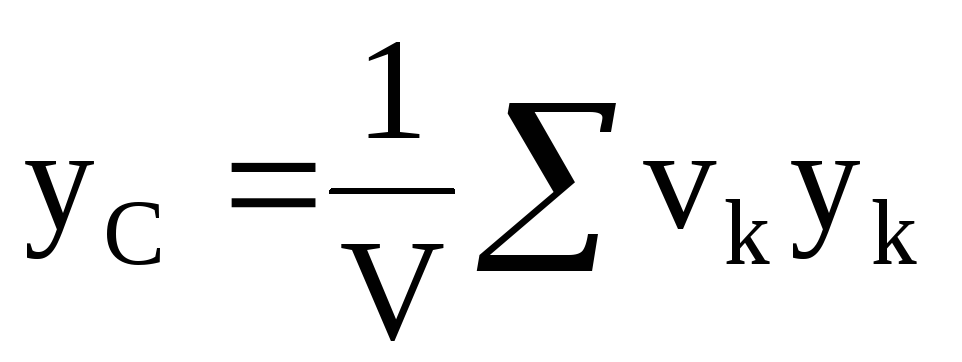
Как видно, положение центра тяжести однородного тела зависит только от его геометрической формы. Поэтому точку С, координаты которой определяются формулами (43), называют центром тяжести объема V.

Путем аналогичных рассуждений легко найти, что если тело представляет собой однородную плоскую и тонкую пластину, то для нее

, , (44)

где S – площадь пластины, s_k – площади ее частей. Точку, координаты которой определяются формулами (44), называют центром тяжести площади S.

Точно также получаются формулы для координат центра тяжести линии:

, , , (45)

где L – длина линии, ℓ_k – длина ее частей.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

§20. Способы определения координат центров тяжести тел

Исходя из полученных выше формул, можно указать способы определения координат центров тяжести тел.

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Из свойств симметрии следует, что центр тяжести однородного круглого кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара лежит в геометрическом центре (центре симметрии) этих тел.

2. Разбиение. Если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести тела можно вычислить по формулам (42) – (45).

3. Дополнение. Этот способ применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.

4. Интегрирование. Тело разбивают на произвольно малые объемы Δv_k, для которых формулы (49) принимают вид

, ,. (46)

где x_k,y_k,z_k – координаты некоторой точки, лежащей внутри объема Δv_k. Затем в равенствах (46) переходят к пределу, устремляя все Δv_kк нулю. Тогда суммы обращаются в интегралы и формулы (46) дают в пределе

,,. (47)

Аналогично для координат центров тяжести площадей и линий получаем:

, . (48)

, , . (49)

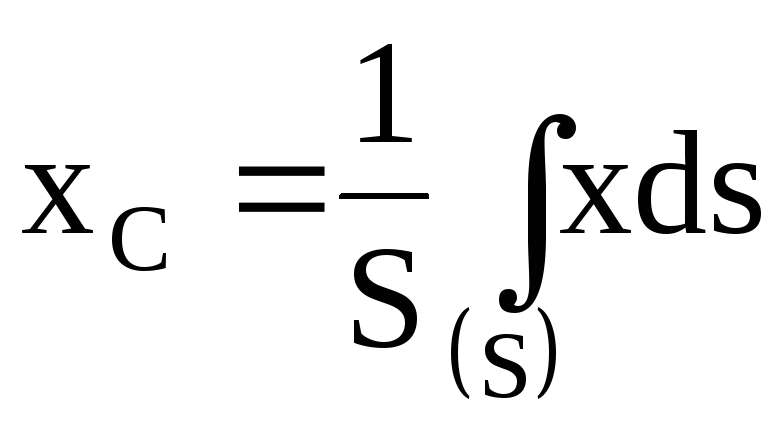
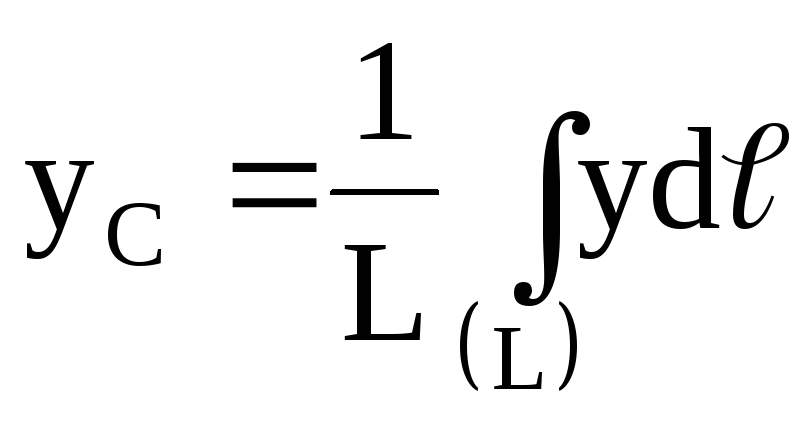
5. Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации (самолет, тепловоз и т.п.) определяют экспериментально.

Источник

Примеры вычисления силовых функций однородного поля силы тяжести и линейной силы упругости

Однородное поле силы тяжести

Рассмотрим материальную точку массой m, находящуюся в однородном поле силы тяжести. Направим ось Oz вертикально вверх, а оси Ox и Oy произвольно в горизонтальной плоскости.

Проекции силы тяжести на оси координат будут равны

Элементарная работа силы тяжести

Так как элементарная работа силы тяжести является полным дифференциалом и , то, интегрируя, находим

(I)

Где А – работа силы тяжести материальной точки массой m на перемещении . (I) можно представить в виде

Где — высота подъема точки.

Если точка расположена выше , т.е. опускается, то работа положительная, иначе – отрицательная.

Поле линейной силы упругости.

Лиин. сила упр. подчиняется закону Гука

Элементарная работа этой силы:

так как . Интегрируем

Таким образом, силовая функция и потенциальная энергия линейной силы упругости является квадратичной формой координат точки М, отсчитываемых от положения равновесия.

Работа силы упругости не зависит от траектории. При перемещении точки из положения равновесия работа силы упругости отрицательна

Поверхностями уровня линейной упругой силы будут концентрические сферы с центром в начале координат, а силовыми линиями – прямые, проходящие через начало координат, т.к. из

25. Закон сохранения полной механической энергии системы.

Если все силы, действующие на систему, потенциальны, то при движении системы её полная механическая энергия постоянна

Пусть все силы, действующие на механическую систему, потенциальны, т.е. существует функция , такая, что

(I)

где — равнодействующая всех сил, приложенных к k-й точке.

Теорема об изм. кин. эн. в дифф. форме:

где . Согласно (I)

Где — потенциальная энергия системы, следовательно,

Сумма кинетической и потенциальной энергии называется полной энергией Е механической системы.

Системы, для которых выполняется закон сохранения механической энергии, называются консервативными.

26. Принцип Даламбера для точки и системы материальных точек.

При движении материальной точки в любой момент времени приложенные к ней активные силы и реакции связей вместе с силой инерции образуют систему сил, эквивалентную нулю (уравновешенную систему сил)

В соответствии с аксиомами статики основное уравнение движения материальной точки имеет вид

— равнодействующая активных сил, — равнодействующая реакций связей.

Запишем уравнение в виде

Слагаемое обозначают и называют даламберовой силой инерции (или просто силой инерции).

При движении механической системы в любой момент времени приложенные силы и реакции связей вместе с силами инерции образуют систему сил, эквивалентную нулю.

(I)

Суммируя левые части по всем точкам

Умножив каждое уравнение векторно слева на радиус-вектор k-й точки и просуммировав их, имеем:

Если силы, приложенные к k-й точке системы, разложить на внешнюю и внутреннюю, а не на активные и реакции связей, то

Так как главный вектор и главный момент относительно произвольного центра приведения внутренних сил системы равен нулю, то

27. Главный вектор и главный момент сил инерции в общем и частном случаях движения твёрдого тела.

При любом движении механической системы главный вектор сил инерции равен взятому со знаком «минус» произведению массы системы

В соответствии с определением главного вектора

Так как ускорение точки , а её масса

Главный момент сил инерции относительно центра приведения О равен взятой со знаком «минус» производной по времени от главного момента количеств движения механической системы относительно того же центра.

Так как

Если движение точек мех. системы рассматривать как сложное, т.е. , то

Где — главный момент количеств движения системы в её относительном движении по отношению к системе координат, движущейся вместе с центром масс. В этом случае главный момент сил инерции относительно неподвижного центра приведения О

Главный момент сил инерции относительно центра масс С

При приведении сил инерции точек тела, вращающегося вокруг неподвижной оси, к произвольному центру О, расположенному на этой оси, в центре О в общем случае должны быть приложены главный вектор и главный момент сил инерции.

28. Связи и их классификация.

Механическая система, точки которой могут занимать любое положения в пространстве и иметь любые скорости, называется свободной.

Если на координаты и скорости точек системы наложены ограничения, то система называется несвободной, а ограничениями называются связями.

Аналитически связь описывается уравнением вида

Ограничивая движения механической системы, связи действуют на её точки посредством сил, которые называются реакциями связей.

При изучении равновесия и движения механических систем методами аналитической механики применяется принцип освобождения (аксиома о связях)

Связи называются голономными, если они описываются уравнениями вида

(I)

Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве.

Неголономными называются связи, которые описываются уравнениями вида

(II)

Уравнения (I), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения на скорости точек, поэтому их называют кинематическими.

Связи подразделяют на стационарныеи нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет.

Связь, уравнение которой имеет вид , является голономной и стационарной. Для голономной нестационарной связи уравнение будет таким

Связь называется удерживающей (двухсторонней), если она описывается уравнением (равенством).

Неудерживающая (односторонняя) связь описывается неравенством.

29. Элементарная работа силы на возможном перемещении. Идеальные связи. Примеры.

Возможной работой силы называется работа силы на любом возможном перемещении точки её приложения

Для вычисления возможной работы можно применять известные формулы для элементарной работы силы, подставляя вместо элементарного действительного возможное перемещение точки.

Если к твердому телу, вращающемуся вокруг неподвижной оси Oz приложена сила , момент которой относительно оси равен

Связи называются идеальными, если равна нулю сумма элементарных работ реакций этих связей на любом возможном перемещении системы (из занимаемого в данный момент времен положения)

Для идеальных связей

— Гладкая поверхность (плоскость) для материально точки

так как вектор расположен вдоль нормали к поверхности и, следовательно, ортогонален вектору возможного перемещения точки.

— Нерастяжимая нить. Реакция нити – сила её натяжения – ортогональна возможному перемещению точки её приложения, поэтому

— Цилиндрические и сферические шарниры, если поверхности соприкасающихся тел считаются идеально гладкими. Если твёрдое тело при помощи шарнира прикреплено к неподвижной опоре, то реакция приложена к неподвижной точке. Возможное перемещение такой точки равно нулю и

Если два твёрдых тела при помощи шарнира с идеально гладкими поверхностями соединены между собой, то

Так как

— Твёрдая шероховатая поверхность для цилиндрического катка при качении без скольжения. Контакт катка с поверхностью происходит по линии. Поэтому реакцией связи является система сил, распределенных вдоль линии контакта. Возможная работа реакции равна нулю, так как они приложены к неподвижным в каждый момент времени точкам – МЦС сечений катка.

30. Принцип возможных перемещений.

Чтобы данное положение механической системы со стационарными идеальными связями было положением равновесия, необходимо и достаточно, чтобы сумма элементарных работ активных сил на любом возможном перемещении системы из этого положения была равна нулю.

Положением равновесия называется такое положение механической системы, в котором она может находится сколь угодно долго, если в начальный момент времени система была приведена в это положение с нулевыми скоростями.

Пусть мех. система из N материальных точек находится в равновесии. Тогда приложенные к каждой точке активные силы и реакции связей уравновешены, т.е.

Умножив каждое равенство на возможное перемещение соответствующей k-й точки и просуммировав скалярное произведение

Если наложенные на систему связи идеальные, то и условие является необходимым условием равновесия системы.

Предположим, что , а система не находится в равновесии. Значит под действием активных сил и реакций связей система за малый промежуток времени совершит некоторое действительное перемещение. При стационарных связях это действительное перемещение совпадает с одним из возможных, поэтому

Так как связи идеальные, то и тогда , что противоречит принятому выше предположению.

31. Общее уравнение динамики (механики)

Источник