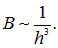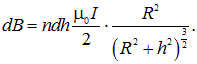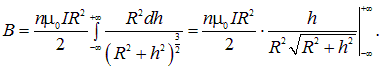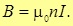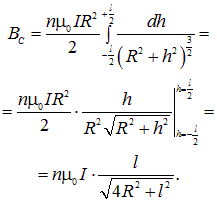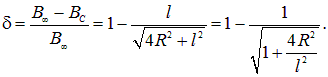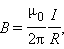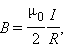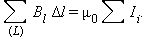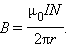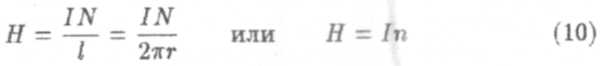однородное магнитное поле создается внутри соленоида
Магнитное поле соленоида. Формула, суть явления.
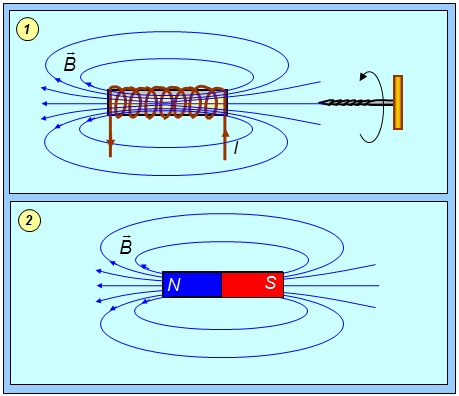
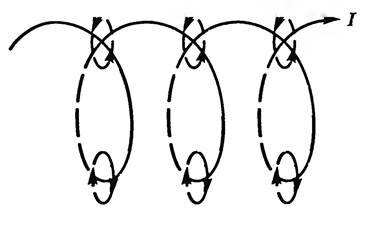
Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков.
Давайте рассмотрим магнитную индукцию, создаваемую каждым витком. Видно, что индукция внутри каждого витка направлена в одну и ту же сторону. Если смотреть в центр витка, то индукция от его краев будет складываться. При этом индукция магнитного поля между двух соседних витков направлена встречно. Так как она создана одним и тем же током то она компенсируется.
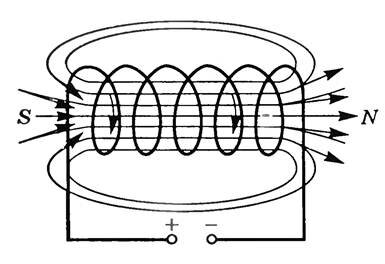
Если витки соленоида намотаны достаточно плотно, то между всеми витками встречное поле будет компенсировано, а внутри витков произойдет сложение отдельных поле в одно общее. Линии этого поля будут проходить внутри соленоида, и охватывать его снаружи.
Если исследовать магнитное поле внутри соленоида любыми способами, например, с помощью железных опилок то можно сделать вывод, что оно однородно. Лини магнитного поля в этой области представляют собой параллельные прямые. Мало того что они параллельны сами себе но они еще параллельны оси соленоида. Выходя за приделы соленоида, они искривляются и замыкаются снаружи катушки.
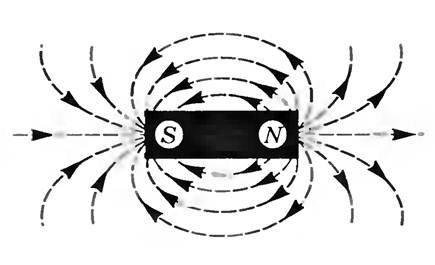
Из рисунка видно, что поле создаваемое соленоидом похоже на поле, которое создает постоянный стержневой магнит. На одном конце силовые линии выходят из соленоида и этот конец аналогичен северному полюсу постоянного магнита. А в другой они входят, и этот конец соответствует южному полюсу. Отличие же заключается в том, что поле присутствует и внутри соленоида. И если провести опыт с железными опилками, то они втянутся в пространство между витками.
Но если внутрь соленоида вставить деревянный сердечник либо сердечник из любого другого немагнитного материала, то при проведении опыта с железной стружкой картина поля постоянного магнита и соленоида будет идентична. Так как деревянный сердечник не исказит силовые лини, но при этом не даст проникнуть опилкам внутрь катушки.
Для определения полюсов соленоида можно использовать несколько методов. Например, самый простой, использовать магнитную стрелку. Она притянется к противоположному полюсу магнита. Если же известно направление тока в витке полюсы можно определить при помощи правила правого винта. Если вращать головку правого винта в направлении тока, то поступательное движение укажет направление поля в соленоиде. А зная, что поле направлено от северного полюса к южному и можно определить, где какой полюс находится.
Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.
Где N число витков соленоида
l длинна соленоида
n число витков на единицу длинны
I Ток в соленоиде
Мю магнитная проницаемость среды находящейся внутри соленоида
6.4. Магнитное поле соленоида
Соленоидом называется цилиндрическая катушка, состоящая из большого числа витков провода, образующих винтовую линию (рис. 6.23-1).
Рис. 6.23. Магнитные силовые линии поля: 1 — соленоида; 2 — полосового магнита
Магнитное поле соленоида напоминает поле полосового магнита (рис. 6.23-2).
Если витки намотаны вплотную, то соленоид — это система круговых токов, имеющих одну ось.
Если считать соленоид достаточно длинным, то магнитное поле внутри соленоида однородно и направлено параллельно оси. Вне соленоида вдали от краев магнитное поле также должно иметь направление параллельное оси и на большом расстоянии от соленоида должно быть очень слабым. Поле убывает по закону
Подсчитаем поле внутри соленоида. Возьмем элемент соленоида длиной dh, находящийся на расстоянии h от точки наблюдения. Если катушка имеет n витков на единицу длины, то в выделенном элементе содержится ndh витков. Согласно формуле (6.11), этот элемент создает магнитное поле
Интегрируя по всей длине соленоида, получаем
Таким образом, поле в бесконечно длинном соленоиде дается выражением
На практике соленоиды бесконечно длинными не бывают. Для иллюстрации рассмотрим некоторые примеры.
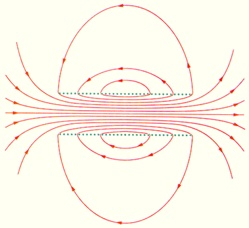
Пример 1. Найти магнитное поле в середине соленоида конечной длины l (рис. 6.24). Сравнить с полем бесконечно длинного соленоида. При каких условиях разница составляет менее 0,5 %?
Рис. 6.24. Магнитное поле катушки конечной длины
В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки
Решение. Магнитное поле в средней точке оси соленоида конечной длины l дается тем же интегралом (6.19), но с другими пределами интегрирования
Если длина соленоида много больше его диаметра (l >> 2R), мы возвращаемся к формуле для поля в бесконечно длинном соленоиде (6.20). Относительная разница этих двух значений равна
По условию эта разница мала: 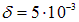
Этот результат легко понять. Представим себе бесконечный соленоид, который мысленно рассекаем пополам в точке наблюдения. Можно считать, что поле в этой точке создается двумя одинаковыми «полубесконечными» соленоидами, расположенными по разные стороны от нее. Ясно, что при удалении одного из них точка наблюдения становится торцом оставшегося «полубесконечного» соленоида, а магнитная индукция в ней уменьшиться именно в два раза.
Это — так называемый краевой эффект. Пример демонстрирует, что недостаточно выполнения соотношения l >> R, чтобы пользоваться формулами для бесконечно длинного соленоида; надо еще, чтобы точка наблюдения находилась далеко от его концов.
На рис. 6.25 представлен опыт по исследованию распределения силовых линий магнитного поля вокруг соленоида. Поле соленоида, ось которого лежит в плоскости пластинки, сосредоточено в основном внутри соленоида. Силовые линии внутри имеют вид параллельных прямых вдоль оси катушки, а поле снаружи практически отсутствует.
Рис. 6.25. Визуализация силовых линий магнитного поля
Видео 6.1. Силовые линии магнитного поля проводников с током различной формы: прямой ток, соленоид, один виток.
Однородное магнитное поле создается внутри соленоида
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции :
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Здесь – расстояние от данного участка Δ до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора 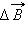
|
которая уже приводилась в § 1.16.
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле
|
где – радиус кругового проводника. Для определения направления вектора 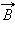
Поясним понятие циркуляции вектора 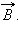
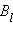
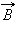
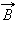
Циркуляцией вектора 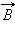
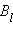
 |
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур в то время, как другие токи могут находиться в стороне от контура.
Теорема о циркуляции утверждает, что циркуляция вектора 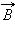
|
Теорема о циркуляции в данном примере выражается соотношением:
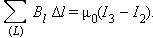 |
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.
Этот пример показывает, что теорема о циркуляции вектора магнитной индукции 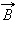
Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 1.17.3).
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса изображена на рис. 1.17.3. Применим теорему о циркуляции к контуру в виде окружности, совпадающей с изображенной на рис. 1.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора 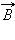
| ∙ 2π = μ0, |
где – полное число витков, а – ток, текущий по виткам катушки. Следовательно,
|
На рис. 1.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри него.
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 1.17.5.
Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки.
Учебники
Журнал «Квант»
Общие
Магнитное поле соленоида
Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны вплотную в одном направлении, а длина катушки значительно больше радиуса витка.
Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке 3 видно, что внутри соленоида линии магнитной индукции каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление.
Поэтому при достаточно плотной намотке соленоида противоположно направленные участки линий магнитной индукции соседних витков взаимно уничтожаются, а одинаково направленные участки сольются в общую линию магнитной индукции, проходящую внутри соленоида и охватывающую его снаружи.Изучение этого поля с помощью опилок показало, что внутри соленоида поле является однородным, магнитные линии представляют собой прямые линии, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида (рис. 4).
Нетрудно заметить сходство между магнитным полем соленоида (вне его) и магнитным полем постоянного стержневого магнита (рис. 5). Конец соленоида, из которого магнитные линии выходят, аналогичен северному полюсу магнита N, другой же конец соленоида, в который магнитные линии входят, аналогичен южному полюсу магнита S.
Полюсы соленоида с током на опыте легко определить с помощью магнитной стрелки. Зная же направление тока в витке, эти полюсы можно определить с помощью правила правого винта: вращаем головку правого винта по току в витке, тогда поступательное движение острия винта укажет направление магнитного поля соленоида, а следовательно, и его северного полюса. Модуль магнитной индукции внутри однослойного соленоида вычисляется по формуле
B=\mu\mu_0 \frac
где Ν — число витков в соленоиде, I — длина соленоида, n — число витков, приходящееся на единицу длины соленоида.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 319-320.
ДОМОСТРОЙСантехника и строительство
Соленоидом называется совокупность N одинаковых витков изолированного проводящего провода, равномерно намотанных на общий каркас или сердечник. По виткам проходит одинаковый ток. Магнитные поля, созданные каждым витком в отдельности, складываются по принципу суперпозиции. Индукция магнитного поля внутри соленоида велика, а вне его — мала. Для бесконечно длинного соленоида индукция магнитного поля вне соленоида стремится к нулю. Если длина соленоида во много раз больше диаметра его витков, то соленоид можно практически считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него и является однородным (рис.6).
Величину индукции магнитного поля внутри бесконечно длинного соленоида можно определить, используя теорему о циркуляции вектора 

Рис.6. Магнитное поле соленоида
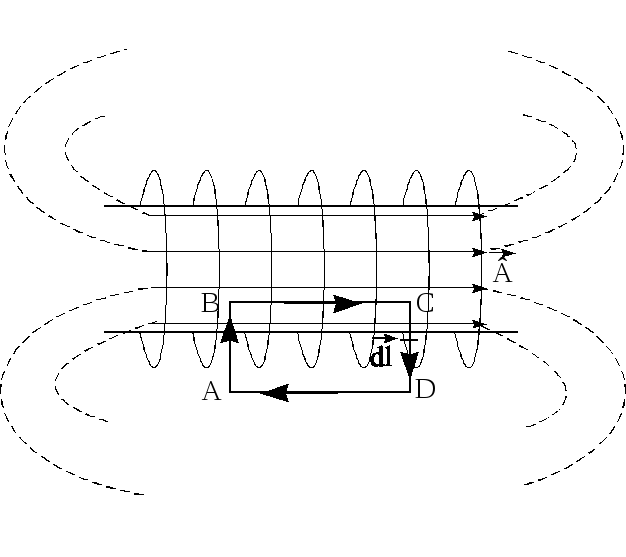
Для определения величины магнитной индукции В внутри соленоида выберем замкнутый контур ABCD прямоугольной формы, где 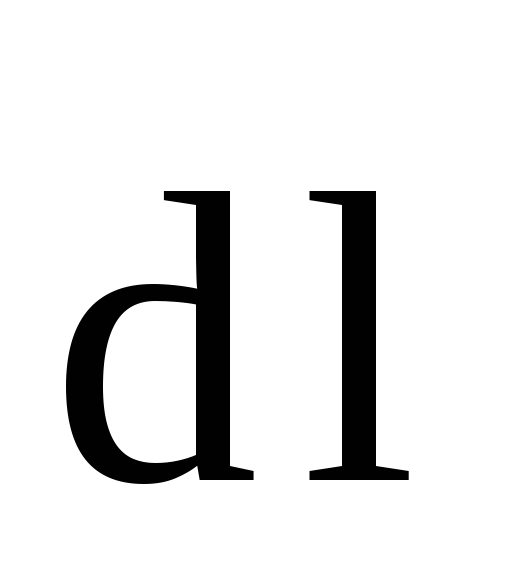
Тогда циркуляция вектора 
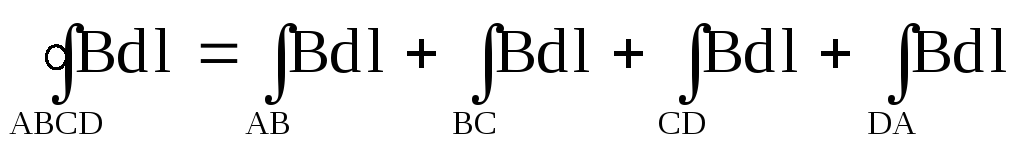
На участках AB и CD произведение 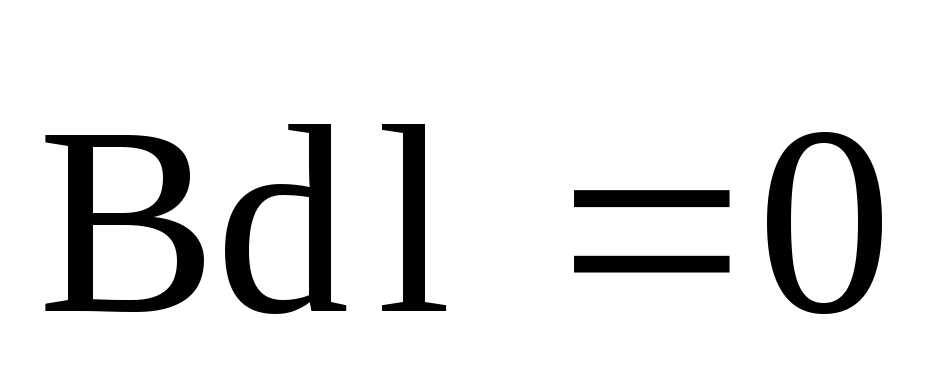


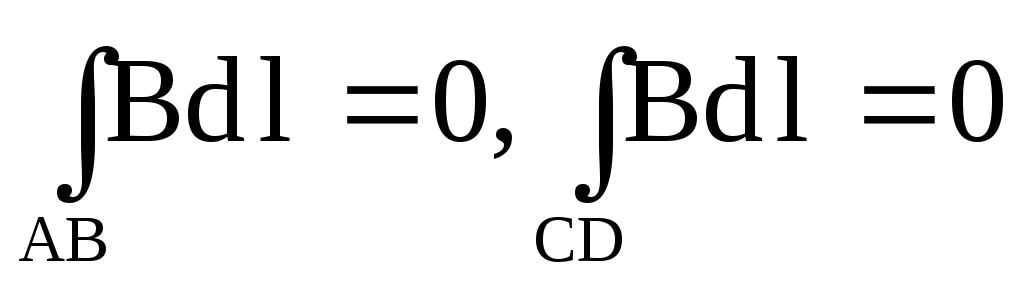
На участке DA вне соленоида интеграл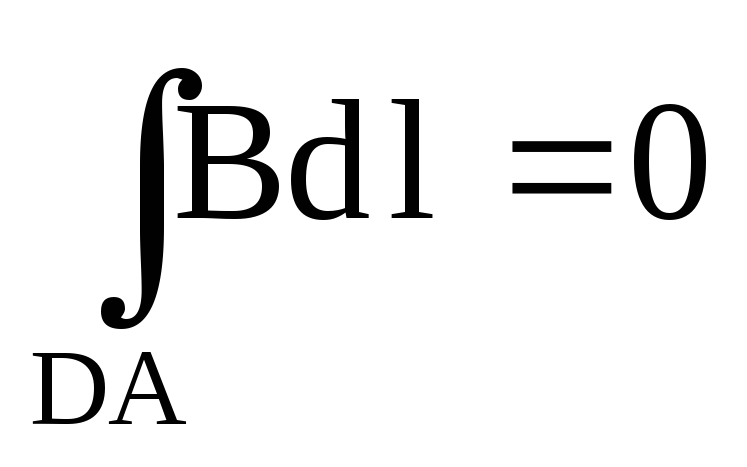
Тогда формула (21) примет вид:
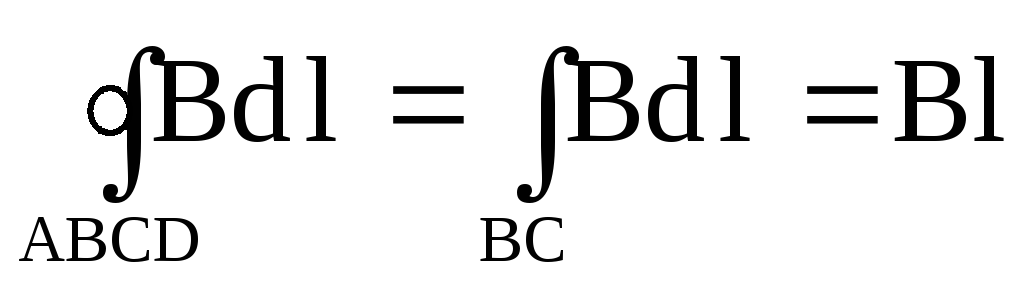
где l – длина участка BC. Сумма токов, охватываемых контуром, равна
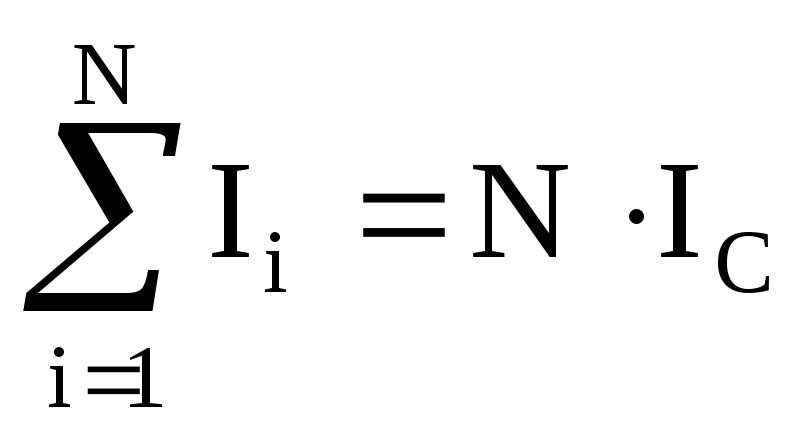
где Ic – сила тока соленоида; N – число витков, охватываемых контуром ABCD.
Подставив (23) и (24) в (20), получим:
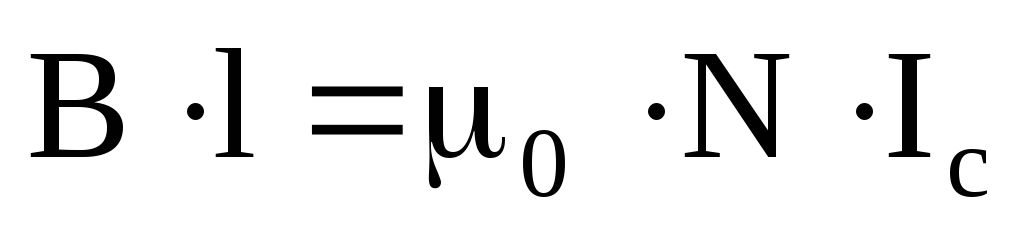
Из (25) получим выражение для индукции магнитного поля бесконечно длинного соленоида:
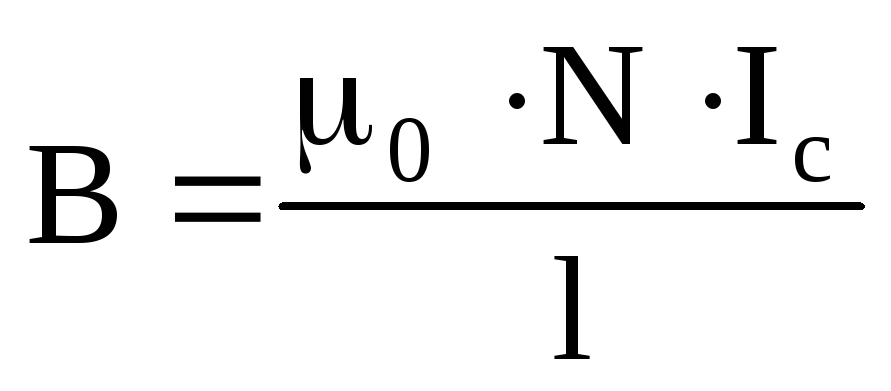
Так как число витков на единицу длину соленоида n равно:
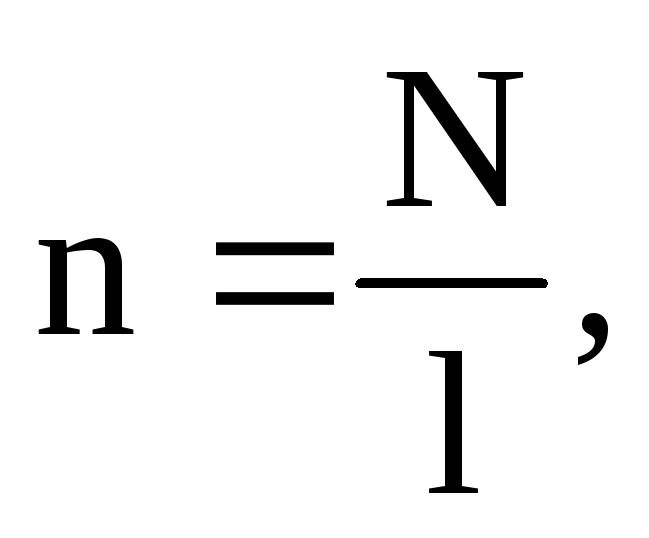
то окончательно получим:
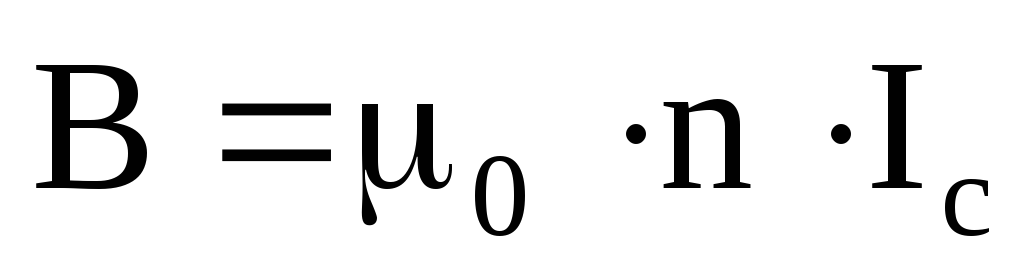
Если внутрь соленоида помещен сердечник, то формула (28) для В примет вид:
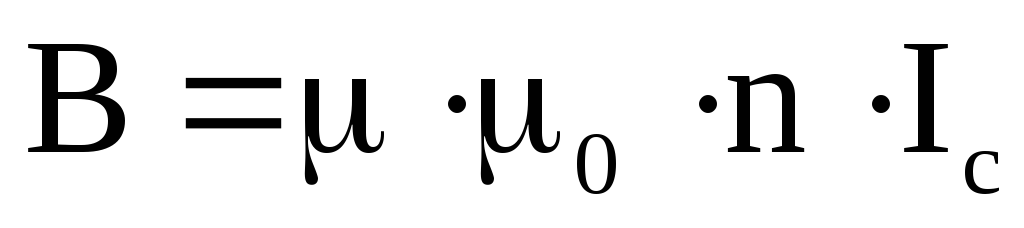
где — магнитная проницаемость материала сердечника.
Таким образом, индукция В магнитного поля соленоида определяется током соленоида Ic, числом витком n на единицу длины соленоида и магнитной проницаемостью материала сердечника.
Цилиндрический магнетрон
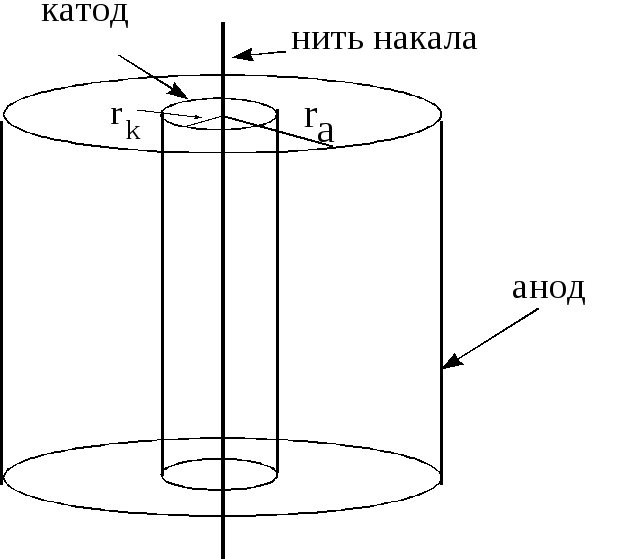
Магнетроном называется двухэлектродная электронная лампа (диод), содержащая накаливаемый катод и холодный анод и помещенная во внешнее магнитное поле.
Анод диода имеет форму цилиндра радиусом 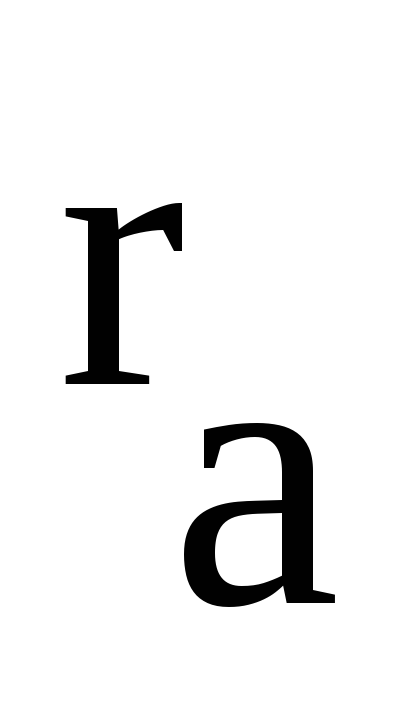
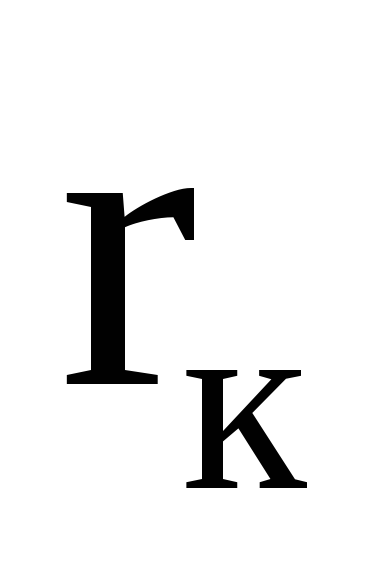
Раскалённый катод в результате явления термоэлектронной эмиссии испускает термоэлектроны, которые образуют вокруг катода электронное облако. При подаче анодного напряжения 

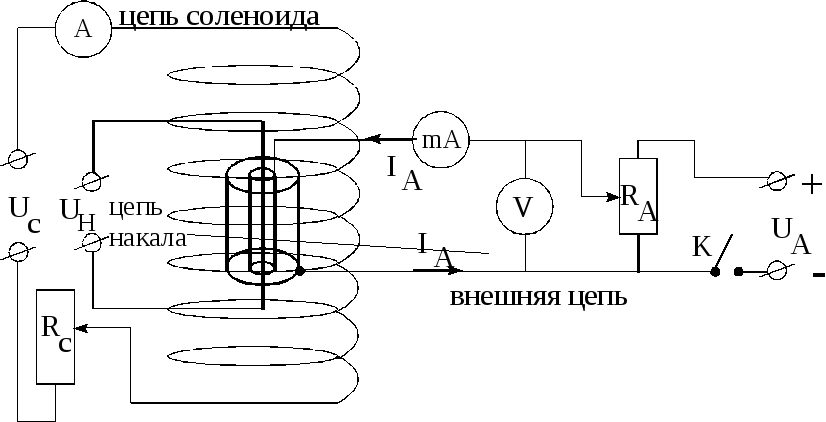
Величина анодного напряжения регулируется потенциометром RA. Чем больше анодное напряжение, тем большее количество электронов за единицу времени достигает анода, следовательно, тем больше анодный ток.
Напряжённость электрического поля Е между катодом и анодом такая же, как и в цилиндрическом конденсаторе:
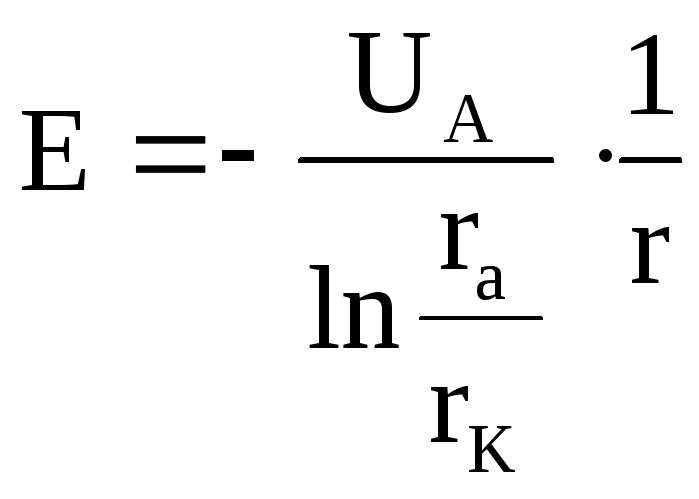
где r – расстояние от оси катода до данной точки пространства между катодом и анодом.
Из формулы (30) следует, что напряжённость поля Е обратно пропорциональна расстоянию r до оси катода. Следовательно, напряженность поля максимальна у катода.
rк Вкр электроны не попадают на анод (рис.9), и анодный ток также будет равен нулю (рис.9, кривая 1).
Однако на практике, вследствие некоторого разброса скоростей электронов и нарушения соосности катода и соленоида, анодный ток уменьшается не скачком, а плавно (рис.9, кривая 2). При этом значение силы тока соленоида, соответствующее точке перегиба на кривой 2, считается критическим Iкр. Критическому значению тока соленоида соответствует анодный ток, равный:
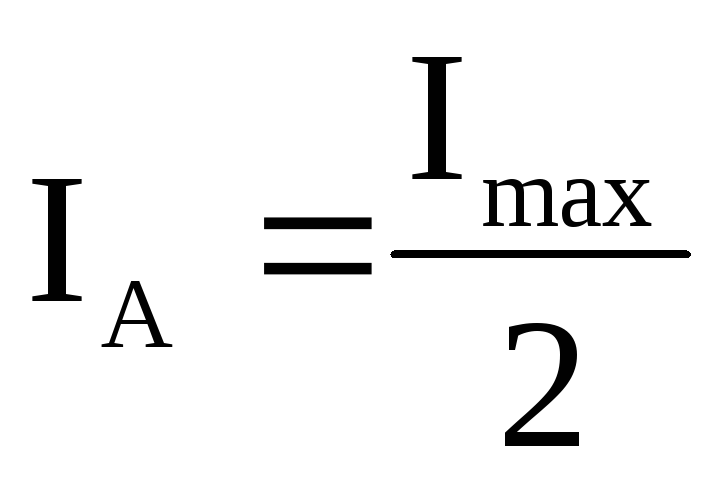
где 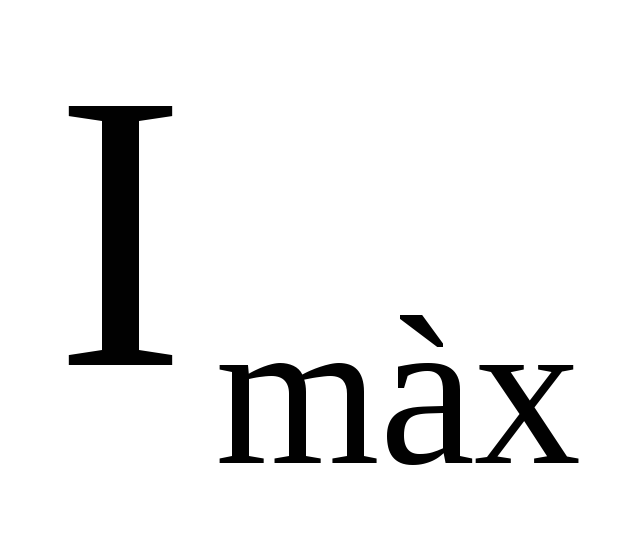
Зависимость анодного тока IA от величины индукции магнитного поля В (или от тока в соленоиде) при постоянном анодном напряжении и постоянном накале называется сбросовой характеристикой магнетрона.
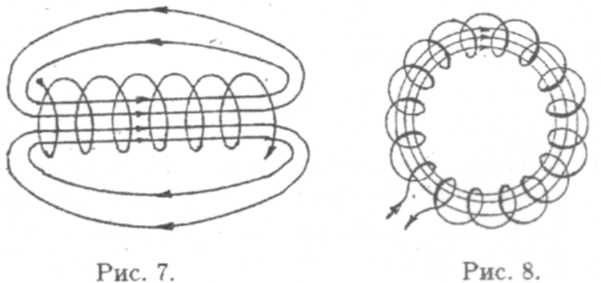
Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны в одном направлении (рис. 7).
Магнитное поле соленоида представляет собой результат сложения полей, создаваемых несколькими круговыми токами, расположенными рядом и имеющими общую ось. Внутри соленоида поле оказывается практически однородным, вне соленоида — неоднородным и сравнительно слабым.
Напряженность поля длинного соленоида (при этом длина соленоида много больше его диаметра, l > d) рассчитывается по формуле
где l —длина соленоида, N — число его витков, I — сила тока в нем. Произведение IN называют числом ампер-витков.
Практически важное значение имеет также магнитное поле тороида — катушки из проволоки, навитой на тор (рис. 8). Магнитное поле тороида однородно и замкнуто внутри тороида. Вне
тороида поле отсутствует. Тороид можно рассматривать как свернутый кольцом достаточно длинный соленоид. Поэтому для расчета напряженности магнитного поля тороида воспользуемся формулой (9), но учтем, что I = 2πr — длине средней линии тороида.
Здесь п — число витков, приходящихся на единицу длины соленоида или тороида.
2. Методика выполнения и рабочие формулы:
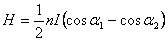
где H — напряженность магнитного поля в А/м; n — число витков на один метр длины обмотки; I — сила тока соленоида; a1 и a2 — углы, под которыми из точки на оси соленоида «видны» радиусы витков соленоида у его ближнего и дальнего концов (рис.1a). Если точка на оси соленоида, в которой вычисляется напряженность магнитного поля, расположена внутри соленоида (рис.1б), то один из углов тупой и формула (I) может быть преобразована к следующему виду ;
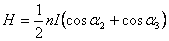
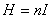
Соответственно, на концах соленоида
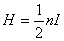
При многослойной обмотке соленоида магнитное поле на его оси является результатом наложения полей, создаваемых отдельными слоями. Поле, создаваемое каждым слоем обмотки соленоида, рассчитывается по формулам (I) и (2). Таким образом, магнитное поле на оси многослойного соленоида качественно не отличается от магнитного поля однослойного соленоида. Количественное различие учитывается при определении числа витков на единицу длины соленоида в формулах (I) и (2).
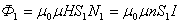
Полный список ВУЗов
Чтобы распечатать файл, скачайте его (в формате Word).