однородное электростатическое поле создано равномерно

Однородное электростатическое поле создано равномерно

Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).

Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

1) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.

2) Пластина имеет отрицательный заряд.

3) Потенциал электростатического поля в точке В ниже, чем в точке С.

4) Напряжённость поля в точке А меньше, чем в точке С.

5) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.

Так как линии напряженности выходят из пластины, то, значит, пластина заряжена положительно (утверждение 2 неверно). Если в точку А поместить пробный точечный отрицательный заряд, то на него будет действовать сила, направленная вертикально вниз (утверждение 1 верно).

Потенциал убывает при удалении от положительной пластины (утверждение 3 неверно).

Напряжённость поля одинакова во всех точках над пластиной (утверждение 4 неверно).

Точки А и B — это точки одинакового потенциала, а значит, работа по перемещению пробного заряда между этими точками равна нулю (утверждение 5 верно).

Источник

Однородное электростатическое поле создано равномерно

Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).

Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

1) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.

2) Пластина имеет отрицательный заряд.

3) Потенциал электростатического поля в точке В ниже, чем в точке С.

4) Напряжённость поля в точке А меньше, чем в точке С.

5) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.

Так как линии напряженности выходят из пластины, то, значит, пластина заряжена положительно (утверждение 2 неверно). Если в точку А поместить пробный точечный отрицательный заряд, то на него будет действовать сила, направленная вертикально вниз (утверждение 1 верно).

Потенциал убывает при удалении от положительной пластины (утверждение 3 неверно).

Напряжённость поля одинакова во всех точках над пластиной (утверждение 4 неверно).

Точки А и B — это точки одинакового потенциала, а значит, работа по перемещению пробного заряда между этими точками равна нулю (утверждение 5 верно).

Источник

Однородное электростатическое поле создано равномерно

Источник задания: Решение 4751. ЕГЭ 2017. Физика. Демидова М. Ю. 30 вариантов.

Задание 16. На рисунке изображены линии напряжённости однородного электростатического поля, образованного равномерно заряженной протяжённой пластиной.

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

1) Заряд пластины положительный.

2) Потенциал в точке В больше, чем в точке С.

3) Работа сил электростатического поля по перемещению точечного положительного заряда из точки А в точку В положительна.

4) Если в точку В поместить точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вверх.

5) Напряжённость поля в точке А меньше, чем в точке С.

1) Вектор напряженности электростатического поля направлен от положительного заряда к отрицательному. Следовательно, пластина имеет положительный заряд.

2) Потенциал электростатического поля тем больше, чем ближе точка к заряду. Точка B ближе к пластине, чем точка C, следовательно, потенциал в точке B выше, чем в точке C.

3) Работа сил электростатического поля по перемещению точечного положительного заряда равна

,

где F – сила Кулона, действующая на заряд; — длина пути, пройденная частицей; — угол между силой и путем перемещения заряда. Кулоновская сила, действующая на заряд, будет направлена вверх к пластине и составлять 90° с путем AB. Так как , то и работа будет равна нулю.

4) Отрицательный заряд в точке B будет притягиваться к пластине (так как разнополярные заряды притягиваются), поэтому на заряд будет действовать сила Кулона, направленная вертикально вниз.

5) Так как электростатическое поле однородно, то напряженность этого поля одинакова во всех точках пространства. Поэтому напряженность поля в точке А равна напряженности в точке С.

Источник

Учебники

Журнал «Квант»

Общие

Закажите стакрил или наливной акрил на сайте Ecovanna-spb

§9. Электрическое поле и его свойства

9.11 Примеры расчета потенциалов электростатических полей.

Поле равномерно заряженной сферы.

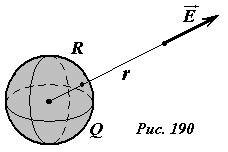
Пусть электрическое поле создается зарядом Q, равномерно распределенным по поверхности сферы радиуса R (Рис. 190). Для вычисления потенциала поля в произвольной точке, находящейся на расстоянии r от центра сферы, необходимо вычислить работу, совершаемую полем при перемещении единичного положительного заряда от данной точки до бесконечности. Ранее мы доказали, что напряженность поля равномерно заряженной сферы вне ее эквивалентно полю точечного заряда, расположенного в центре сферы. Следовательно, вне сферы потенциал поля сферы будет совпадать с потенциалом поля точечного заряда

В частности, на поверхности сферы потенциал равен \(

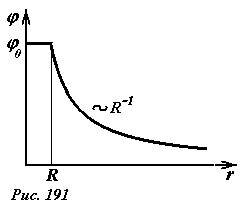
Итак, распределение потенциала поля равномерно заряженной сферы имеет вид (Рис. 191)

Обратите внимание, поле внутри сферы отсутствует, а потенциал отличен от нуля! Этот пример является яркой иллюстрацией, того, что потенциал определяется значением поля от данной точки до бесконечности.

Поле равномерно заряженного кольца.

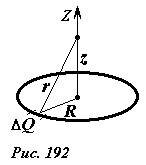
Вычислим потенциал поля, создаваемого зарядом Q, равномерно распределенным по тонкому кольцу радиуса R, причем ограничимся расчетом потенциала поля только на оси кольца (Рис. 192). Ранее мы вычислили напряженность поля на оси кольца, как функцию расстояния до его центра. Поэтому для вычисления потенциала можно, в принципе, подсчитать работу, совершаемую полем при перемещении заряда от данной точки до бесконечности. Однако, в данном случае проще воспользоваться принципом суперпозиции для потенциала поля. Для этого мысленно разобьем кольцо на малые участки, несущие заряд ΔQ_k. Тогда в точке, находящейся на расстоянии z от его центра, этот заряд создает поле, потенциал которого равен

Так как все точки кольца находятся на одинаковом расстоянии \(

r = \sqrt \) от рассматриваемой точки, то суммирование потенциалов полей, создаваемых зарядами ΔQ_k сводится к суммированию самих зарядов

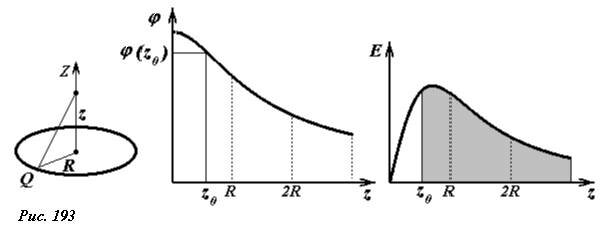
График этой функции показан на рисунке. Там же повторен график зависимости напряженности поля кольца на его оси от расстояния до центра кольца. Напомним, что значения потенциала φ(z₀) в точке с координатой z₀ численно равно площади под графиком зависимости E(z) в интервале от z₀ до \(

Обратите внимание – так как проекция вектора напряженности не изменяет свой знак, то функция φ(z) является монотонной.

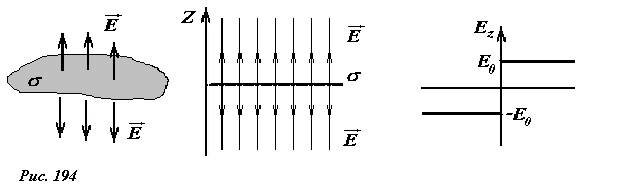
Поле равномерно заряженной бесконечной пластины.

Ранее мы показали, что электрическое поле, создаваемое бесконечной равномерно заряженной пластиной является однородным, то есть напряженность поля одинакова во всех точках, причем вектор напряженности направлен перпендикулярно плоскости, а его модуль равен \(

При традиционном выборе нулевого уровня потенциала \(

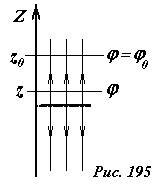
Поэтому следует воспользоваться произволом выбора нулевого уровня. Достаточно выбрать произвольную точку с координатой z = z₀, и приписать ей произвольное значение потенциала φ(z₀) = φ(₀) (Рис. 195). Теперь, чтобы вычислить значение потенциала в произвольной точке φ(z), можно воспользоваться соотношением между напряженностью и потенциалом поля \(

из которого следует искомая зависимость потенциала от координаты (при z > 0)

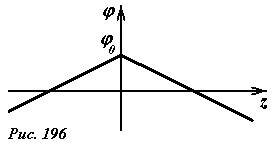
В частности, можно задать произвольное значение потенциала самой пластины, то есть положить при z = z₀ = 0 φ = φ(₀). Тогда значение потенциала в произвольной точке определяется функцией

график которой показан на рисунке 196.

То, что потенциал относительно бесконечности оказался бесконечно большим, вполне очевидно – ведь и бесконечная пластина обладает бесконечно большим зарядом. Как мы уже подчеркивали, такая система является идеализацией – бесконечных пластин не существует. В реальности все тела имеют конечные размеры, поэтому для них традиционный выбор нулевого потенциала возможен, правда в этом случае распределение поля может быть очень сложным. В рамках же рассматриваемой идеализации удобнее воспользоваться использованным нами выбором нулевого уровня.

Задание для самостоятельной работы.

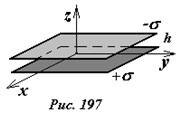
Поле двух параллельных равномерно заряженных пластин.

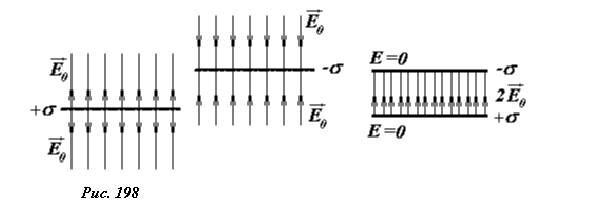
Каждая равномерно заряженная пластина создает однородное поле, модуль напряженности которого равен \(

Складывая напряженности полей по принципу суперпозиции, получим, что в пространстве между пластинами напряженность поля \(

E = 2E_0 = \frac<\sigma><\varepsilon_0>\) вдвое превышает напряженность поля одной пластины (здесь поля отдельных пластин параллельны), а вне пластин поле отсутствует (здесь поля отдельных пластин противоположны).

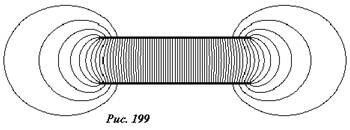
Строго говоря, для пластин конечных размеров поле не является однородным, силовые линии поля пластин конечных размеров показаны на рисунке 199. Наиболее сильные отклонения от однородности наблюдаются вблизи краев пластин (часто эти отклонения называют краевыми эффектами). Однако, в области прилегающей к середине пластин поле с высокой степенью точности можно считать однородным, то есть в этой области можно пренебречь краевыми эффектами. Заметим, что погрешности такого приближения тем меньше, чем меньше отношение расстояния между пластинами к их размерам.

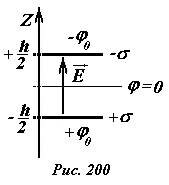
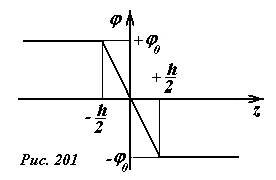
Для однозначного определения распределения потенциала поля, необходимо выбрать уровень нулевого потенциала. Будем считать, что потенциал равным нулю в плоскости расположенной по средине между пластинами, то есть, положим φ = 0 при z = 0.

Не смотря на произвол в выборе нулевого уровня потенциала, наш выбор может быть логически обоснован на основании симметрии системы. Действительно, рассматриваемая система зарядов зеркально повторяет себя при зеркальном отражении относительно плоскости z = 0 и одновременном изменении знаков зарядов. Поэтому желательно, чтобы и распределение потенциала обладало такой же симметрией: восстанавливалось при зеркальном отражении с одновременным изменением знака всех функций поля. Выбранный нами способ выбора нулевого потенциала удовлетворяет такой симметрии.

Задания для самостоятельной работы.

Источник

Задание №16 ЕГЭ по физике

Описание задания

Для решения задания №16 нужно знать основы электростатики, а также явление электромагнитной индукции и законы, связанные с нею.

В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.

Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.

а) период колебаний силы тока в контуре

б) фаза колебаний напряжения на конденсаторе

в) заряд конденсатора

г) энергия магнитного поля катушки

д) амплитуда колебаний напряжения на катушке

Алгоритм решения

Решение

В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.

Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.

Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.

Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.

В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Катушка индуктивности подключена к источнику тока с пренебрежимо малым внутренним сопротивлением через резистор Ом (см. рисунок). В момент ключ К замыкают. Значения силы тока в цепи, измеренные в последовательные моменты времени с точностью 0,01 А, представлены в таблице.

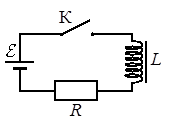
Выберите два верных утверждения о процессах, происходящих в цепи.

Алгоритм решения

Решение

Согласно утверждению 1, напряжение на резисторе в момент времени t = 1,0 c равно 1,9 В. Так как сила тока еще не установилась, а сопротивление источника тока пренебрежимо мало, вычислить напряжение на резисторе можно с помощью закона Ома для полной цепи:

Следовательно, утверждение 1 — неверно.

Согласно утверждению 2, энергия катушки максимальна в момент времени t = 0 c. Энергия катушки определяется формулой:

Так как сила тока в начальный момент времени равна нулю, то энергия катушки в это время тоже нулевая.

Следовательно, утверждение 2 — неверно.

Согласно утверждению 3, ЭДС источника тока равна 18 В. Вычислить ЭДС источника тока можно, используя закон Ома для полной цепи в момент, когда сила тока в цепи достигнет максимального значения. В этом случае ЭДС самоиндукции будет равна 0. Тогда:

Это действительно так. Следовательно, утверждение 3 — верно.

Согласно утверждению 4, напряжение на катушке максимально в момент времени t = 6,0 c. Напряжение на катушке равно разности напряжения ЭДС источника тока и напряжения на резисторе (так как они соединены последовательно):

Так как значение силы тока в момент времени t = 6,0 с максимально, то напряжение на катушке. Следовательно, утверждение 4 — неверно.

Согласно утверждению 5, модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В. Проверяя истинность утверждения 3, мы выяснили, что ЭДС источника тока равна 18 В. Следовательно, ЭДС самоиндукции равна:

Для вычислений используем значения из таблицы для момента времени t = 2,0 с:

Следовательно, утверждение 5 — верно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Протон в однородном магнитном поле движется по окружности. Чтобы в этом поле двигалась по окружности с той же скоростью α-частица, радиус окружности, частота обращения и энергия α-частицы по сравнению с протоном должны:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Сила Лоренца определяется формулой:

Если вместо протона взять альфа-частицу, то заряд увеличится вдвое, так как альфа-частица содержит 2 протона. Сила Лоренца прямо пропорционально зависит от величины заряда. Следовательно, она тоже увеличится вдвое. Скорость движения заряда по условию задачи остается постоянной, как и модуль вектора магнитной индукции.

Сила Лоренца будет сообщать альфа-частице центростремительное ускорение, равное:

Применим второй закон Ньютона:

Заряд альфа-частицы больше заряда протона вдвое. Она также содержит 2 нейтрона, поэтому ее масса примерно в 4 раза больше массы протона. Следовательно, радиус движения альфа-частицы увеличится примерно вдвое.

Частота обращения альфа-частицы связана с ее линейной скоростью формулой:

Так как скорость остается постоянной, то при увеличении радиуса частота обращения должна уменьшиться.

Энергия альфа-частицы будет больше, чем у протона, вращающегося с той же скоростью. Это связано с тем, что ее кинетическая энергия будет примерно в 4 раза больше (так как во столько раз больше ее масса).

pазбирался: Алиса Никитина | обсудить разбор | оценить

Катушка № «>№ 1 включена в электрическую цепь, состоящую из источника напряжения и реостата. Катушка № «>№ 2 помещена внутрь катушки № «>№ 1 и замкнута (см. рисунок).

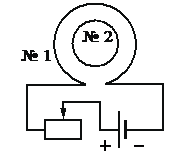
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процессы в цепи и катушках при перемещении ползунка реостата вправо.

А) Сила тока в катушке № 1 увеличивается.

Б) Вектор индукции магнитного поля, созданного катушкой № 1, всюду увеличивается.

В) Магнитный поток, пронизывающий катушку № 2, увеличивается.

Г) Вектор индукции магнитного поля, созданного катушкой № 2, в центре этой катушки направлен от наблюдателя.

Д) В катушке № 2 индукционный ток направлен по часовой стрелке.

Алгоритм решения

Решение

Согласно утверждению А, при перемещении ползунка реостата вправо сила тока в катушке №1 увеличивается. Перемещая ползунок реостата вправо, мы увеличиваем сопротивление. Следовательно, сила тока уменьшается. Утверждение А — неверно.

Согласно утверждению Б, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №1, всюду увеличивается. Так как сила тока уменьшается, вектор индукции магнитного поля ослабевает. Утверждение Б — неверно.

Согласно утверждению В, при перемещении ползунка реостата вправо магнитный поток, пронизывающий катушку №2, увеличивается. Так как магнитное поле ослабевает, будет уменьшаться и магнитный поток, пронизывающий катушку № 2. Утверждение В — неверно.

Согласно утверждению Г, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки направлен от наблюдателя. В катушке №1 ток течёт по часовой стрелке, и по правилу буравчика эта катушка будет создавать магнитное поле, направленное от наблюдателя. В силу того, что сила тока в цепи уменьшается, будет уменьшаться и магнитный поток, пронизывающий вторую катушку. При этом согласно правилу Ленца во второй катушке будет создаваться индукционный ток, который направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван. В этом случае вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки сонаправлен с внешним полем и направлен от наблюдателя. Утверждение Г — верно.

Согласно утверждению Д, при перемещении ползунка реостата вправо в катушке №2 индукционный ток направлен по часовой стрелке. По правилу правой руки, индукционный ток в катушке 2 направлен по часовой стрелке. Утверждение Д — верно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Конденсатор подключён к источнику тока последовательно с резистором R=20 кОм (см. рисунок). В момент времени t=0 ключ замыкают. В этот момент конденсатор полностью разряжен. Результаты измерений силы тока в цепи представлены в таблице.

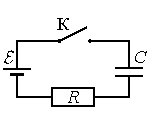
Внутренним сопротивлением источника и сопротивлением проводов пренебречь. Выберите два верных утверждения о процессах, наблюдаемых в опыте.

а) Ток через резистор в процессе наблюдения увеличивается.

б) Через 6 с после замыкания ключа конденсатор полностью зарядился.

в) ЭДС источника тока составляет 6 В.

г) В момент времени t = 3 с напряжение на резисторе равно 0,6 В.

д) В момент времени t = 3 с напряжение на конденсаторе равно 5,7 В.

Алгоритм решения

Решение

Согласно утверждению «а», ток через резистор в процессе наблюдения увеличивается. Но это не так, поскольку в таблице с течением времени сила тока уменьшается. Утверждение «а» неверно.

Согласно утверждению «б», через 6 с после замыкания ключа конденсатор полностью зарядился. Если это было бы так, то сила тока была бы равна 0. Но в момент времени t = 6 с она равна 1 мкА. Следовательно, утверждение «б» неверно.

Согласно утверждению «в», ЭДС источника тока составляет 6 В. Напряжение в цепи в начальный момент времени равно ЭДС источника. Следовательно:

Вывод: утверждение «в» верное.

Согласно утверждению «г», в момент времени t = 3 с напряжение на резисторе равно 0,6 В. Чтобы проверить это, нужно умножить соответствующую силу тока на сопротивление резистора:

Вывод: утверждение «г» неверное.

Согласно утверждению «д», в момент времени t = 3 с напряжение на конденсаторе равно 5,7 В. Чтобы проверить это, нужно из ЭДС в этот момент времени вычесть напряжение на внешней цепи. Его мы уже нашли. Оно равно 0,3 В. ЭДС мы тоже нашли. Она равна 6 В. Их разность равна 5,7 В. Следовательно, утверждение «д» верно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Однородное электростатическое поле создано равномерно заряженной протяжённой горизонтальной пластиной. Линии напряжённости поля направлены вертикально вверх (см. рисунок).

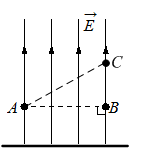
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

1) Пластина имеет отрицательный заряд.

2) Потенциал электростатического поля в точке В ниже, чем в точке С.

3) Работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю.

4) Если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз.

5) Напряжённость поля в точке А меньше, чем в точке С.

Алгоритм решения

Решение

Согласно утверждению 1, пластина имеет отрицательный заряд. Известно, что векторы напряженности поля, создаваемого отрицательным зарядом, направляются в сторону этого заряда. Но мы видим, что векторы направляются от заряда. Следовательно, пластина заряжена положительно, а утверждение 1 неверно.

Согласно утверждению 2, потенциал электростатического поля в точке В ниже, чем в точке С. Известно, что потенциал зависит от расстояния до отрицательно пластины. Поскольку в нашем случае пластина заряжена положительно, с увеличением расстояния от нее потенциал уменьшается. Поэтому потенциал в точке С меньше потенциала в точке В, а утверждение 2 неверно.

Согласно утверждению 3, работа электростатического поля по перемещению пробного точечного отрицательного заряда из точки А и в точку В равна нулю. Работа определяется формулой:

Видно, что работа зависит от перемещения относительно заряженной пластины. Но точки А и В находятся от пластины на одинаковом расстоянии. Следовательно, перемещение относительно нее равно 0. Поэтому работа по перемещению заряда тоже будет нулевой, и утверждение 3 верно.

Согласно утверждению 4, если в точку А поместить пробный точечный отрицательный заряд, то на него со стороны пластины будет действовать сила, направленная вертикально вниз. Это действительно так. Мы выяснили, что пластина заряжена положительно. Следовательно, отрицательный заряд будет притягиваться к ней, и утверждение 4 верно.

Согласно утверждению 5, напряжённость поля в точке А меньше, чем в точке С. Это не так, потому что речь идет об однородном поле. Напряженность однородного поля одинакова во всех точках, и утверждение 5 неверно.

Верные утверждения: 3 и 4.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Введите ответ в поле ввода Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Емкость конденсатора определяется формулой:

Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.

Вот как взаимосвязана электроемкость и заряд конденсатора:

Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.

С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник