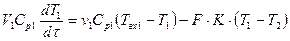одномерное стационарное температурное поле

Температурное поле. Тепловой поток

Одним из основных параметров, определяющих характер теплообмена, является температура.

Температурным полемназывается совокупность значений температуры в каждый момент времени во всех точках рассматриваемого пространства.

Температура может изменяться в направлении одной, двух или всех трёх осей координат. В соответствии с этим различают одномерные, двухмерныеи трёхмерные поля температур. Одномерное стационарное температурное поле описывается формулой вида: .

Изотермическими поверхностями называются поверхности, представляющие собой геометрическое место точек с одинаковой температурой.

Такие поверхности не могут пересекаться друг с другом. Они могут быть замкнутыми или ограничиваются наружными границами тела.

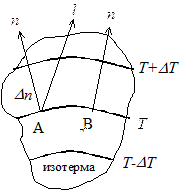
Изотермами называются линии пересечения изотермических поверхностей с какой-либо плоскостью (рис. 1.1).

С помощью изотермических поверхностей или изотерм можно графически изобразить вид температурного поля в данный момент времени.

Как видно на рис. 1.1, в ближайшей окрестности точки А температура изменяется во всех направлениях, не совпадающих с плоскостью, касательной к

Рис. 1.1. Изотермические поверхности

изотермической поверхности . Но наиболее значительное изменение температуры имеет место в направлении по нормали к изотермической поверхности.

Градиентом температуры называется производная температуры по нормали к изотермической поверхности:

grad T =

Градиент температуры является вектором, направленным по нормали к изотермической поверхности в сторону увеличения температуры, — единичный вектор нормали. Выражение grad T = определяет модуль градиента температуры, т.е. приращение температуры на единице длины этой нормали.

Интенсивность изменения температуры в произвольном направлении s (рис. 1.1) меньше, чем в направлении нормали, и равна проекции вектора градиента температуры на это направление: .

Тепловым потокомназывается количество теплоты, проходящее через данную поверхность с площадью F в единицу времени.

Он обозначается символом Q. Единицей измерения Q является Дж/с, т.е. ватт (Вт).

Плотностью теплового потока называется количество теплоты, проходящей через единицу поверхности в единицу времени. Она обозначается символом q и измеряется в Вт/м . Таким образом, .

Q ,

Источник

Температурное Поле

Аналитическое исследование теплопроводности сводится к изучению пространственно-временного изменения так называемого температурного поля, характерного для рассматриваемого процесса,

, (11.1)

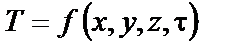
где Т – температура; x, y, z – пространственные координаты в декартовой системе; t – время; f – обозначение функции, определяющей зависимость температуры Т от координат x, y, z и времени t.

Различают стационарное и нестационарное температурное поле.

Выражение (11.1) представляет собой математическую запись нестационарного температурного поля, зависящего не только от пространственных координат x, y, z, но и от времени t.

Стационарным температурным полем называется такое поле,

, , (11.2)

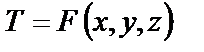
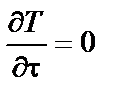
значение которого в любой его точке не изменяется во времени, т.е. является функцией только пространственных координат x, y, z.

Температурные поля (11.1) и (11.2) являются трехмерными, так как являются функциями трех координат. Если температура есть функция только двух пространственных координат x, y

; (11.1а)

, (11.2а)

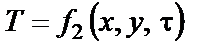
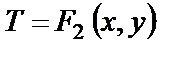
то температурные поля (11.1а), (11.2а) называют двухмерными. Если же температуры представляют собой функции одной пространственной координаты х

; (11.1b)

, (11.2b)

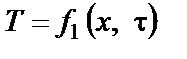
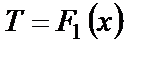
то соответствующие температурные поля (11.1b), (11.2b) называются одномерными.

Примером одномерных температурных полей могут служить:

— поле неограниченной пластины, ширина и длина которой очень велики по сравнению с ее толщиной;

— поле неограниченного цилиндра, длина которого очень велика по сравнению с его диаметром (радиусом);

Принимая во внимание, что температура является скалярной величиной, можно утверждать, что температурное поле является скалярным полем.

Если точки поля, имеющие одинаковые температуры, соединить, то получится изотермическая поверхность. Пересечение изотермической поверхности плоскостью дает на этой поверхности изотерму (линию, соответствующую одинаковой температуре).

Вдоль изотермической поверхности температура не изменяется. Наибольшее изменение температуры на единицу длины происходит в направлении нормали n к изотермической поверхности и характеризуется градиентом температуры, представляющим собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры

,

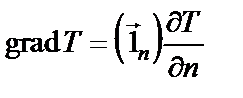
где ( 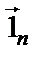) – единичный вектор, направленный по нормали в сторону возрастания температуры; – производная температура по направлению нормали n к изотермической поверхности.

Градиент температуры gradT часто обозначают также символом ÑТ. Составляющие градиента температуры по осям декартовой системы координат равны соответствующим частным производным

, (11.3)

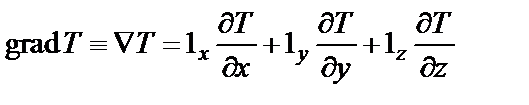
где 1_x, 1_y, 1_z – ортогональные между собой векторы единичной длины, направленные вдоль осей x, y, z соответственно; 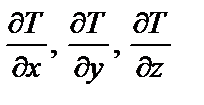– частные производные температуры T (x, y, z, t) по координатам x, y, z.

Дата добавления: 2015-02-16 ; просмотров: 2970 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Температурное поле и его изменения

Распространение тепла в материальных средах, в частности, в конструкциях зданий, всегда связано с различным тепловым состоянием отдельных зон или участков пространства, вызванным природными условиями или деятельностью человека (например, теплый воздух в отапливаемом помещении и холодный снаружи, нагретые участки помещения у приборов отопления и охлажденные у окон и т. д.). Происходящие процессы теплопередачи приводят к постоянному или изменяющемуся во времени распределению температур в рассматриваемой материальной среде или конструкции. Одновременное распределение температур в рассматриваемой материальной системе называется температурным полем. Закономерности теплопередачи непосредственным образом связаны с распределением температур и особенностями температурного поля.

Рис. 1.2. Изолинии температур двумерного поля В строительной теплофизике пространственные температурные поля рассматриваются сравнительно редко, поскольку для практических целей в большинстве случаев достаточно изучить двумерное температурное поле, возникающее в одной из проекций, т. е. в плане или разрезе конструкций. В этом случае, при установившихся условиях теплопередачи, температура в каждой точке проекции конструкции является функцией двух координат: t=f(x, у).

Третья координата (т. е. высота или длина конструкции) предполагается достаточно протяженной, а потому не влияющей на распределение температур в плоском сечении.

Рис. 1.3. Однородное температурное поле в плоской протяженной стене Закономерность изменений температурного поля наиболее наглядно можно представить, нанеся линии равных температур (изотермы) в изучаемой проекции конструкции. Наиболее резкое изменение температуры отмечается по нормали к изолиниям (рис. 1.2). Эта нормаль совпадает с направлением температурного градиента (повышения температур) между изолиниями и противоположна (обратна на 180°) наиболее вероятному направлению теплового потока Q, переносящего тепло от более высокой температуры к более низкой. В однородной плоской бесконечно протяженной стене с постоянной разностью температур на противоположных поверхностях эти изолинии параллельны друг другу и поверхностям ограждения; направление потока тепла возможно для этой конструкции только в одном направлении (рис. 1.3), а функциональная зависимость изменений температуры наиболее проста: t=f(x). Это случай наиболее элементарного одномерного температурного поля в установившихся (стационарных) условиях теплопередачи.

Рис. 1.4. Изолинии двумерного температурного поля и направления потоков тепла Изолинии температур в конструкциях с более сложной геометрической формой выражаются двумерным температурным полем и обычно не параллельны поверхностям ограждения, а криволинейны. При криволинейном очертании изотерм пути распространения тепла Q (нормальные к изотермам) также не могут быть параллельными друг другу, как это видно из рис. 1.4, на котором показано двумерное температурное поле простенка наружной стены, выполненного из трехслойных панелей.

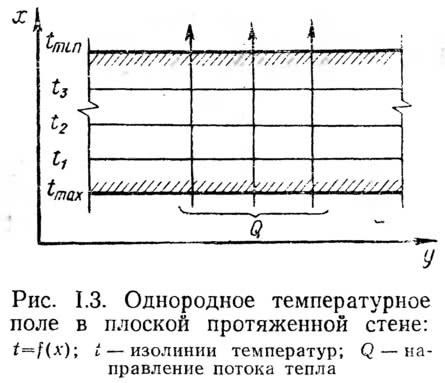
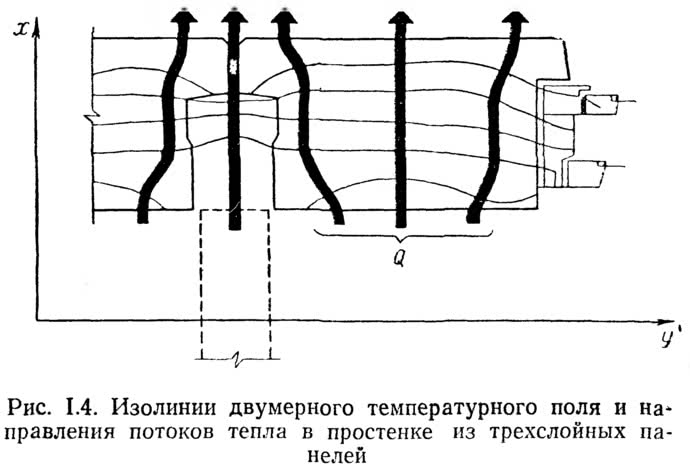
При установившихся условиях теплопередачи внешние тепловые воздействия (значения и разность температур) постоянны (или принимаются таковыми в целях упрощения расчетов процессов передачи тепла, которые без особых погрешностей можно свести к установившимся условиям).

В действительных условиях внешние тепловые воздействия (например, наружные температуры) изменяются во времени, что приводит к нестационарной теплопередаче и изменчивости температурного поля.

В теплофизических расчетах ограждающих конструкций зданий важное значение имеет рассмотрение температурного поля этих конструкций при периодических изменениях внешних воздействий (например, периодическое охлаждение или прогрев, вызванные циклическим режимом производства, периодической теплоотдачей отопительных систем, ежедневным облучением солнцем и т. д.). Та-кое нестационарное температурное поле, для которого характерны закономерные периодические изменения, называют квазистационарным.

Во всех возможных случаях разработки приближенных инженерных методов расчета предпочтение отдается более простым и, в частности, основанным на рассмотрении закономерностей стационарного температурного поля. Иногда это приводит к некоторому повышению запасов теплофизической надежности рассчитываемых ограждающих конструкций, поскольку внешние воздействия, влияющие на распределение температур, приходится принимать наиболее неблагоприятными из числа закономерно возможных.

Так, например, теплофизический расчет ограждающих конструкций для холодного периода года проводится по условиям предельно возможного охлаждения конструкции, наступающего при таком наиболее низком значении температуры наружного воздуха, которое в соответствии с климатическими условиями может не изменяться в течение времени, необходимого для постепенной стабилизации наиболее неблагоприятного температурного поля в рассматриваемой конструкции.

Примечания

1. Эта функциональная раскрывается в дифференциальном уравнении Лапласа.

2. См. дифференциальное уравнение Фурье.

Источник

Температурное поле

Теплопроводность

Процесс теплопроводности, как и другие виды теплообмена, может иметь место только при условии, что в различных точках тела (или системы тел) температура неодинакова. В общем случае процесс распространения теплоты теплопроводностью в теле сопровождается измене­нием температуры, как в пространстве, так и во времени. Температурное состояние тела (или системы тел) можно охарактеризовать с помощью температурного поля.

Температурным полем называют совокупность значений температу­ры во всех точках тела для каждого времени.

Поскольку температура различных точек тела определяется ко­ординатами x, y, z и временем τ, то в общем случае уравнение температурного поля имеет вид:

(1)

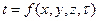
Различают стационарные и нестационарные температурные поля. Если температура в точках тела не изменяется во времени, то такое температурное поле называют стационарным или установившимся, если же температура меняется во времени, то поле называют нестационар­ным или неустановившимся.

Температура в теле может меняться в направлении одной, двух или трех координатных осей. В соответствии с этим различают одно­мерные (линейные), двухмерные (плоскостные) и трехмерные (пространственные) температурные поля.

В соответствии с изложенной классификацией температурных по­лей уравнение (1) описывает трехмерное нестационарное поле.

Уравнение трехмерного стационарного поля имеет вид:

; (2)

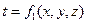
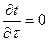
Уравнение одномерного нестационарного поля принимает вид:

; (3)

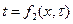
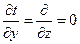
Наиболее простой вид имеет уравнение одномерного стационар­ного температурного поля:

; ; (4)

Источник

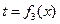
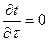
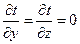
Температурное поле

Температурным полем называется совокупность значений температур в данный момент времени во всех точках рассматриваемого пространства, занятого теплом.

Если температура поля с течением времени t изменяется, то оно называетсянестационарным и описывается уравнением:

где x,y,z – координаты точки поля.

Если же температура в каждой точке поля с течением времени t, остается неизменной, то такое температурное поле называетсястационарным. Температура, в этом случае, является функцией только пространственных координат

В каждый момент времени в температурном поле можно выделить поверхности, имеющие одинаковые температуры. Такие поверхности называются изотермическими. В стационарном температурном поле изотермические поверхности с течением времени не меняют свой вид и расположение, в то время как в нестационарном поле они со временем изменяются.

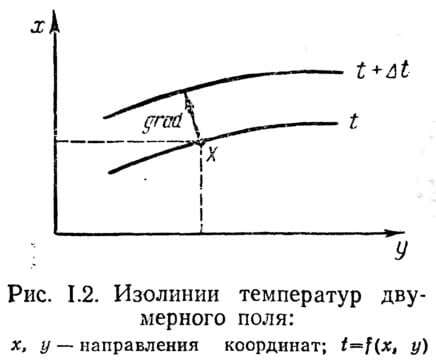
Одной из характеристик температурного поля является температурный градиент, представляющий собой вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры. На рис.4.1. изображены изотермические поверхности, температуры которых отличаются на DТ.

Рис. 1. К понятию температурного градиента

Из рисунка видно, что интенсивность изменения температуры по разным направлениям (из точки А лучи п и l) неодинакова. Наибольшая разность температур на единицу длины наблюдается в направление нормали п к изотермической поверхности в точке А, так как расстояние между соседними изотермами Dn при этом меньше, чем в точке В.

Предел отношения изменения температуры DТ к расстоянию между изотермами по нормали Dn, когда Dn стремится к нулю, называетсятемпературным градиентом:

В общем случае для различных точек одной и той же изотермической поверхности (например, для точек А и В) градиент температуры различен не только по направлению, но и по величине. За положительное направление градиента принято направление возрастания температур.

Основы теплового расчета

Несмотря на многообразие конструкций и принципов работы теплообменных аппаратов, процессы теплообмена в них подчиняются общим закономерностям, а основные положения методики их расчета могут быть рассмотрены в общей постановке.

До недавнего времени расчет теплообменных аппаратов приводился только для стационарных режимов, и при этом в основном решались две задачи:

1. Для заданных параметров на входе и выходе из аппарата и типе теплообменной поверхности определить требуемую площадь поверхности теплообмена и произвести его конструктивную разработку. Это есть проектный расчет.

2. Для реально существующего аппарата при заданных параметрах потоков на входе определить количество передаваемой теплоты и параметры потоков на выходе из аппарата. Это задача проверочного расчета.

К этим двум задачам можно добавить третью, так называемый оптимальный расчет теплообменного аппарата. Решение этой задачи возможно благодаря использованию ЭВМ. Суть этой задачи сводится к расчету оптимального теплообменника по выбранному критерию.

Тепловой расчет теплообменных аппаратов базируется на уравнениях теплового баланса и теплопередачи.

Решение нестационарных задач теплообмена возможно только при использовании математических моделей, записанных на основе моделей структуры потоков теплоносителей.

Проектный расчет теплообменного аппарата

Задачей проектного расчета является определение геометрических размеров и режима работы теплообменника, необходимого для отвода или подвода заданного количества теплоты к теплоносителю.

При проектном расчете задают:

1. Тип аппарата и общие геометрические характеристики поверхности теплообмена (размеры труб, оребрения, толщина стенок и др.).

2. Параметры теплоносителей на входе и выходе из аппарата (температура, давление и т.д.)

3. Тепловую мощность аппарата Q или расход сред.

Взаимность изменений температур теплоносителей определяется условием теплового баланса, которое для бесконечно малого элемента теплообменника имеет вид:

Здесь G₁, G₂, C_p1, C_P2 – расходы и теплоемкости теплоносителей 1 и 2, T₁ и Т₂ – их температуры в произвольном сечении аппарата. Уравнение теплового баланса для всего аппарата получается путем интегрирования уравнения (4.4) и имеет вид:

Уравнение (4.5) содержит две неизвестные: G₁ или G₂ и T_k1 или T_k2. Следовательно, это уравнение является неопределенным. Общий прием решения этих задач заключается в использовании метода последовательных приближений, состоящего в том, что в начале принимаются определенные решения относительно конструкции аппарата и неизвестных технологических параметров, затем путем пересчета проверяется до получения результатов с желаемой степенью точности.

Проверочный расчет теплообменного аппарата

Целью проверочного расчета теплообменного аппарата заданной конструкции является определение его мощности и температур потоков на выходе Т_k1, T_k2 при заданных площадях поверхности теплообмена F, расхода сред G₁, G₂ и их температурах на входе Т_h1 и Т_h2.

Математические модели теплообменников

Обычно принимают, что движение потоков теплоносителя и хладоагента характеризуется гидродинамическими моделями идеального смешения, идеального вытеснения, ячеечной моделью ОДМ или их комбинацией.

Если гидродинамическая структура потоков в теплообменном аппарате соответствует модели идеального смешения, то во всем потоке происходит полное смешение молекул потока. В таком случае любое изменение температуры потока на входе в зону идеального смешения мгновенно распространяется по всему объему зоны.

Гидродинамическая структура потоков теплоносителя, соответствующая модели идеального смешения, имеет место в теплообменных аппаратах с изменением агрегатного состояния потоков – в конденсаторах, кипятильниках, испарителях. Уравнение, описывающее изменение температуры для теплообменника в зоне идеального смешения, имеет вид:

, (6)

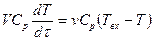
где V – объем зоны идеального смешения; v – объемная скорость; Т_вх, Т – температура потока на входе и в зоне идеального смешения; С_р – теплоемкость потока; t – время.

Условие физической реализуемости модели идеального вытеснения выполняются в случае поршневого потока, когда предполагается, что в направлении его движения смещение полностью отсутствует, а в направлении, перпендикулярном движению, происходит идеальное смешение. Гидродинамическая структура потоков, соответствующая модели идеального вытеснения, характерна для движения потоков в трубном пространстве кожухотрубчатых теплообменников различных конструкций, а также для теплообменного аппарата типа «труба в трубе».

Уравнение, описывающее изменение температуры в зоне идеального вытеснения, имеет вид:

, (7)

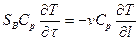
где S_b – сечение зоны идеального вытеснения; l – координата длины аппарата.

Диффузионная модель гидродинамической структуры потоков соответствует такому движению потоков, когда в направлении его движения существует продольное смещение, а перпендикулярном направлении предполагается наличие идеального смешения.

Диффузионная модель значительно лучше, чем модель идеального вытеснения, описывает гидродинамические условия в реальных кожухотрубчатых теплообменниках. Уравнение, характеризующее изменение температуры по длине зоны, имеет вид:

, (8)

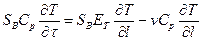
где е_т – коэффициент продольного переноса теплоты.

Температуры потоков в теплообменных аппаратах могут изменяться в каждой точке потока не только в результате его движения, но также из-за теплообмена с окружающей средой или за счет источника теплоты. Интенсивность источника теплоты записывается следующим образом:

где F – поверхность теплообмена, отнесенная к единице объема; К – коэффициент теплопередачи; DТ – разность температур.

Уравнения (4.6) и (4.7) для температур потока с учетом источника теплоты в потоке имеет вид:

;(10)

. (11)

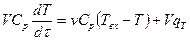
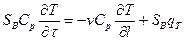
Учитывая (4.9) и зная, что V = S*L из (4.11) получим:

или

. (12)

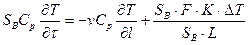
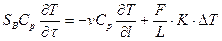
Аналогично для ДДМ с учетом (4.9) имеем:

. (13)

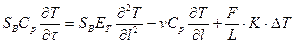
Для описания гидродинамической структуры потоков в реальных теплообменных аппаратах используются комбинированные модели движения потоков: ячеечная модель; модель идеального смешения с застойной зоной; модель идеального смешения с байпасом; последовательное соединение двух моделей МИС и МИВ. Применение таких моделей для описания гидродинамической структуры потоков позволяет описать изменение профиля температур как по длине, так и в объеме теплообменного аппарата.

Теплообменник типа «перемешивание-перемешивание»

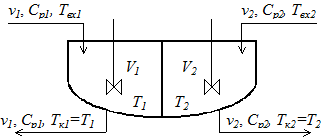
Математическая модель такого теплообменника (рис.4.2) представляет собой систему уравнений типа (4.7), записанных для теплоносителя и хладоагента:

, (14)

где T₁ – T₂ = DT, при этом T₁ и T₂ имеют постоянные значения в каждой точке объема идеального перемешивания V₁ и V₂; Т_вх1, Т_вх2 – температуры первичного и вторичного теплоносителей на входе в аппарат; Т_к1 = Т₂ и Т_к2 = Т₂ – конечные температуры первичного и вторичного теплоносителей. Величина FK(T₁ – T₂) имеет знак «минус» в уравнении описания потока теплоносителя, который отдает тепло, и знак «плюс», если тепло воспринимается теплоносителем.

Рис. 2. Схематическое изображение теплообменника типа «перемешивание-перемешивание»

Теплообменник типа «перемешивание-вытеснение»

Математическая модель такого теплообменника (рис.4.3) включает уравнение модели идеального перемешивания для потока теплоносителя и уравнение модели идеального вытеснения для хладоагента:

;

, (15)

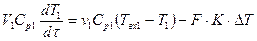
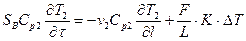
где DT = T₁ – T₂ при этом значения T₁ остается одинаковыми в каждой точке объема идеального перемешивания, а Т₂ изменяются по длине зоны идеального вытеснения.

Теплообменник типа «вытеснение-вытеснение»

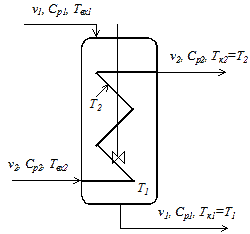
Рассмотрим моделирование широко распространенного в химической технологии теплообменника «труба в трубе», структура потоков которого соответствует модели «вытеснение – вытеснение» (рис.3.1).

Рис.4. Схема теплообменника типа «труба в трубе»

Это так называемый прямоточный теплообменник, для которого модель имеет вид:

;

, (16)

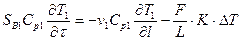
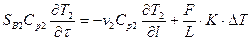
где DT = T₁ – T₂, при этом Т₁ и Т₂ изменяются по длине соответствующих зон идеального вытеснения. Цель работы: построить математическую модель и рассчитать теплообменный аппарат с известной структурой потоков.

Дата добавления: 2015-08-01 ; просмотров: 10600 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник