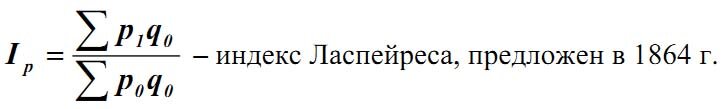общий индекс в статистике

Экономические индексы в статистике: понятие, виды, формулы. Примеры решения задач

Как известно, «индекс» в переводе с латинского означает «указатель» или «показатель». В статистике индексом называют показатель относительного изменения данного уровня исследуемого явления по сравнению с другим его уровнем, принятым за базу сравнения. В качестве такой базы может быть использован или уровень за какой-либо прошлый период времени (динамический индекс), или уровень того же явления по другой территории (территориальный индекс).

В статистической практике индексы являются незаменимым инструментом исследования в тех случаях, когда необходимо сравнить во времени или пространстве две совокупности, элементы которых непосредственно суммировать нельзя. В целом, индексный метод направлен на решение следующих задач:

Простейшим показателем, используемым в индексном анализе, является индивидуальный индекс (i), который характеризует изменение во времени экономических величин, относящихся к одному объекту:

В тех случаях, когда исследуются не единичные объекты, а состоящие из нескольких элементов совокупности, используются сводные (общие) индексы (I). Исходной формой сводного индекса является агрегатная форма. Формулы для вычисления общих индексов представлены в таблице.

Примеры решения задач по теме «Экономические индексы в статистике»

Задача 1. По нижеприведенным данным ответить на вопросы, поставленные в таблице, т.е. определить недостающие показатели.

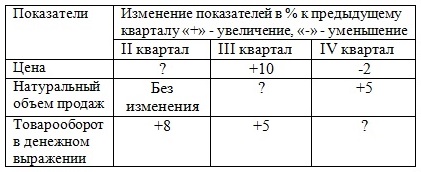Решение

3) ІV квартал: Ip =0,98; Iq = 1,05; Ipq =?
Ipq = Ip×Iq = 0,98×1,05 = 1,029 ≈ 1,03 (в таблицу поместим +3).

Итак, заполним таблицу:

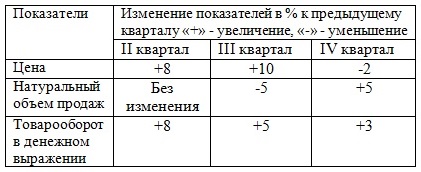Задача 2. Имеется информация о выпуске продукции на предприятии, ее себестоимости за 2 квартала.

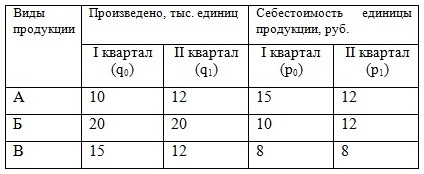Определить: 1) индивидуальные индексы количества и себестоимости; 2) общие индексы затрат на производство, натурального выпуска и себестоимости; 3) абсолютное изменение затрат на выпуск продукции в целом и по факторам: а) за счет изменения себестоимости; б) за счет изменения натурального выпуска. Сделать выводы.

Решение

1) Найдем индивидуальные индексы количества:
для продукции А: i_q = q₁/q₀ = 12/10=1,2;
для продукции Б: i_q = q₁/q₀ = 20/20=1;
для продукции В: i_q = q₁/q₀ = 12/15=0,8

Найдем индивидуальные индексы себестоимости:
для продукции А: i_p = p₁/p₀ = 12/15=0,8;
для продукции Б: i_p = p₁/p₀ = 12/10=1,2;
для продукции В: i_p = p₁/p₀ = 8/8=1

2) общие индексы затрат на производство, натурального выпуска и себестоимости найдем по формулам:

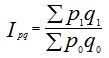= (12*12+12*20+8*12)/(15*10+10*20+8*15) = 480/470 = 1,021=102,1%

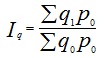= (12*15+20*10+12*8)/470 = 476/470 = 1,013 = 101,3%

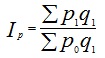3) абсолютное изменение затрат на выпуск продукции в целом:

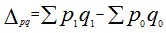По факторам: а) за счет изменения себестоимости:

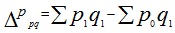б) за счет изменения натурального выпуска

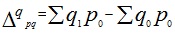Вывод: Товарный выпуск во втором квартале увеличился по сравнению с первым на 102,1-100=2,1%. В абсолютном выражении это соответствует 10 тыс. руб. Этот рост произошел как за счет увеличения объема выпуска (на 101,3-100=1,3% или 6 тыс. руб.), так и за счет себестоимости (100,8-100=0,8% или 4 тыс. руб.).

Задача 3. Имеется информация о затратах на производство и индексах количества:

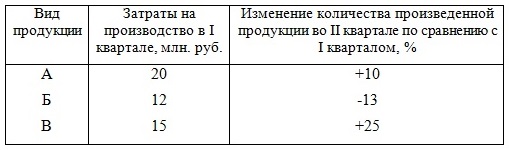Определить: 1)индивидуальные индексы физического объема производства; 2) общий индекс физического объема производства; 3) общий индекс себестоимости, если известно, что общие затраты на производство выросли на 25%. Сделать выводы.

Решение

1) Найдем индивидуальные индексы количества:
для продукции А: i_q = q₁/q₀ = (100+10)/100 = 110/100=1,1;
для продукции Б: i_q = q₁/q₀ = (100-13)/100 = 87/100=0,87;
для продукции В: i_q = q₁/q₀ = (100+25)/100 = 125/100=1,25

Далее найдем общий индекс объема производства:

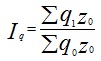3) Поскольку общие затраты на производство выросли на 25%, то общий индекс затрат Izq = 1,25.
Найдем общий индекс себестоимости: Iz = Izq:Iq = 1,25:1,089 = 1,148 =114,8%

Вывод: Увеличение общих затрат на производство во втором квартале на 25% произошло как за счет увеличения объема выпуска на 108,9-100=8,9%, так и за счет увеличения себестоимости на 114,8-100= 14,8%.

Другие статьи по данной теме:

Список использованных источников

2012 © Лана Забродская. При копировании материалов сайта ссылка на источник обязательна

Источник

Общие индексы

Поможем написать любую работу на аналогичную тему

Если изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, экономический анализ выполняют посредством общих индексов. Индекс становится общим, когда в его расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Действительно нельзя, например, складывать непосредственно килограммы мяса и рыбы, так как полученный результат в прямом смысле не являлся бы «ни рыбой, ни мясом».

Любые общие индексы могут быть построены 2-мя способами: как агрегатные и как средние из индивидуальных.

Агрегатный индекс является основной и наиболее распространенной формой индекса, если числитель и знаменатель представляют собой набор – «агрегат» (от лат. aggregatus – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов – сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для целей соизмерения индексируемых величин.

Например, общую сумму выручки можно записать в виде агрегата (суммы произведений объемного показателя q на взвешивающий – p), т.е.

Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так получают индекс общего объема товарооборота (выручки), показывающий во сколько раз он изменился (или сколько процентов составляет) в отчетном периоде по сравнению с базисным:

IQ=. (184)

Разность между числителем и знаментелем формулы (184) представляет собой абсолютное изменение общего товарооборота (выручки) (185), показывающее на сколько в денежных единицах (например, рублях) он изменился в отчетном периоде по сравнению с базисным:

Например, дедушка торговал яблоками двух сортов: «антоновкой» и «белым наливом», результаты торговли за 2 дня представлены в таблице 51:

Таблица 51. Условные данные о торговле яблоками дедушкой за 2 дня

Рассчитаем выручку дедушки по формуле (183):

– в отчетном периоде: ∑Q1= 18*160+25*120 = 5880 (руб.) – это выручка от продажи яблок сегодня;

– в базисном периоде: ∑Q0= 20*100+22*150 = 5300 (руб.) – это выручка от продажи яблок вчера.

Теперь определим изменение общей выручки дедушки:

– по формуле (184): IQ= 5880/5300 = 1,1094, то есть выручка увеличилась в 1,1094 раза, или на 10,94%.

– по формуле (185): ∆∑Q = 5880 – 5300 = 580, то есть выручка увеличилась на 580 руб.

При анализе изменения общего объема товарооборота (выручки) это изменение также объясняется изменением уровня цен и количества проданных товаров. Влияние этих факторов выражается агрегатными индексами физического объема (количества) и цен.

Если уровни взвешивающего показателя взяты по данным базисного периода, то получают агрегатный индекс Ласпейреса:

; (186) . (187)

Формула (186) применяется, когда количество – это 1-ый фактор, а формула (187) – когда цена является 1-ым фактором.

Если уровни взвешивающего показателя взяты по данным отчетного периода, то получают агрегатный индекс Пааше:

; (188) . (189)

Формула (188) применяется, когда количество – это 2-ой фактор, а формула (189) – когда цена является 2-ым фактором.

Произведение агрегатных индексов Ласпейреса и Пааше дает общий индекс выручки:

IQ =; (190) IQ = . (191)

В нашем примере про дедушку (как и в примере про бабушку) цена яблок – это 1-ый фактор, а количество – 2-ой. Поэтому для определения агрегатного индекса цен применяем формулу (187):

= 1,0472, то есть цена на яблоки увеличилась в 1,0472 раза (на 4,72%).

Определим агрегатный индекс количества проданных яблок по формуле (188):

= 1,0594, то есть количество проданных яблок выросло в 1,0594 раза (на 5,94%).

Контроль правильности расчетов производим по формуле (191): IQ= 1,0472*1,0594 = 1,1094, то есть изменение общей выручки дедушки в 1,1094 раза (на 10,94%) объясняется изменением цены в 1,0472 раза (на 4,72%) и изменением количества продаж в 1,0594 раза (на 5,94%).

Из формул (186) – (189) видно, что индексы Ласпейреса и Пааше по одному и тому же фактору не равны между собой, то есть ≠ и ≠. Амери­канский экономист Гершенкрон обширными расчетами установил, что по одному и тому же фактору индекс Ласпейреса обычно больше индекса Пааше, и это открытие названо эффектом Гершенкрона[56], то есть > и >.

Когда нет возможности определить очередность влияния факторов на результативный показатель (какой из факторов 1-ый – цена или количество) проблематично выбрать одну из формул (186) или (187) и (188) или (189). В таких случаях рекомендуется применить все формулы (186) – (189) и рассчитать среднюю геометрическую величину из однофакторных индексов – индексы Фишера:

; (192) . (193)

Сравнивая значения индексов Фишера, которые показывают среднее изменение цен (193) и количества (192), решается вопрос об очередности влияния факторов: какой из индексов показывает большее изменение, тот фактор и считают 1-ым.

Из формул (190) и (191) легко получить двухфакторные мультипликативные индексные модели общей выручки, подставив в них формулу (184) и выразив ∑Q1:

∑Q1= Q0, (194) ∑Q1= Q0. (195)

Формула (194) применяется, когда количество товара – 1-ый фактор, а цена 2-ой, а формула (195) – наоборот, цена – 1-ый фактор, а количество – 2-ой. Тогда, применяя метод Чалиева, можно выполнить факторный анализ, то есть объяснить изменение результативного показателя (общей выручки) изменением каждого фактора (цен и количества) в отдельности в абсолютных (денежных) единицах. Более детальный анализ изменения итогового показателя возможен при изучении так называемых структурных сдвигов.

В нашем примере про дедушку мы применяли формулу (187), значит должны производить факторный анализ по модели (195). Тогда, применяя метод Чалиева, изменение общей выручки ∆∑Q = ∑Q1 – ∑Q0 объясняется изменением:

1) количества проданных проданных яблок ∆∑Qq = (–1) ∑Q0 =(1,0594–1)*5300 ≈ 315 (руб.)

2) цены яблок ∆∑Qp = (–1) ∑Q0 =1,0594*(1,0472–1)*5300 ≈ 265 (руб.)

Проверка правильности расчета влияния факторов: ∆∑Q = 265 + 315 = 580, что совпадает с общим изменением общей выручки, рассчитанным ранее по формуле(185).

Помимо записи общих индексов в агрегатной форме на практике часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов. Так, общий индекс выручки может быть записан как средняя арифметическая взвешенная (196) или средняя гармоническая взвешенная (197) из индивидуальных индексов выручки по отдельным товарным группам:

(196) (197)

В формуле (196) весами являются показатели объема товарооборота отдельных товарных групп в отчетном периоде, в формуле (197) – в базисном.

Аналогично через индивидуальных индексы количества товара и цены могут быть выражены общие агрегатные индексы Ласпейреса и Пааше:

; (198) ; (199)

; (200) . (201)

Источник

Общие индексы

При помощи общих индексов, как отмечалось выше, чаще всего и характеризуется изменение экономических явлений и процессов.

В отличие от индивидуальных индексов их построение и исчисление является делом более сложным, этим занимается теория индексов.

По методологии расчета общие индексы подразделяются на:

Основной формой экономических индексов в отечественной практике являются агрегатные. Они состоят из 2-х частей:

Соизмеритель (вес) вводится в индекс для того, чтобы преодолеть несуммарность отдельных элементов изучаемого явления. Т.е. при помощи весов суммируются наборы (агрегаты) индексируемых показателей. Соизмеритель (вес) экономически тесно связан с индексируемой величиной и приводит элементы сложного явления к сопоставимому виду. Для этого веса берутся одинаковыми в числителе и знаменателе индекса.

Агрегатный индекс цен

Рассмотрим основные принципы и методы расчета агрегатных индексов на примере индекса цен и индекса физического объема товарооборота.

Если в качестве индексируемой величины выступает цена, т.е. нам необходимо определить общее изменение цен на различные товары, то чтобы преодолеть несуммарность цен следует:
– ввести в индекс соизмеритель (вес) в виде количества проданных (или произведенных) товаров.

Тогда произведение цен на количество соответствующих товаров даст стоимости этих товаров. А стоимости различных товаров уже можно суммировать.

Следовательно, в индексах цен в качестве соизмерителя (веса) индекса, выступают количества товаров. Причем, эти количества должны быть одни и те же для текущего и для базисного периода, чтобы индекс отразил только изменение уровня цен.

Таким образом, общее изменение цен на различные товары можно определить путем расчета агрегатного индекса цен введя в него в качестве веса одинаковую величину: количества проданных товаров за текущий или базисный период.

Придерживаясь принятых выше обозначений и приняв в качестве веса количество проданных товаров за текущий период, формулу агрегатного индекса цен можно представить в виде:

где p1 и p0 – цена единицы проданных товаров в текущем и базисном периоде соответственно;
q1 – количество проданных товаров в текущем периоде.

Если же принять в качестве весов данные о количестве проданных товаров в базисном периоде, то формула агрегатного индекса цен будет иметь следующий вид:

Агрегатные индексы цен, полученные по этим 2-м формулам – с текущим и базисными весами, не идентичны. Они имеют разное экономическое содержание.

Индекс Пааше характеризует изменение цен текущего периода, по сравнению с базисным, на товары, реализованные в текущем периоде.

Т.е. он позволяет рассчитать экономический эффект, который имел место при изменении цен. Изменение цен, как известно, приводит к определенному перераспределению средств в народном хозяйстве:

Индекс Ласпейреса показывает, насколько изменились цены в текущем периоде по сравнению с базисным, на товары, которые были реализованы в базисном периоде.

Т.е. он позволяет рассчитать некий условный экономический эффект, условную экономию или перерасход средств. Поэтому при расчете индекса цен используется, как правило, 1-я формула индекса с весами текущего периода, потому, что экономиста интересует не условная экономия или перерасход, а фактический экономический эффект от изменения цен.

Таким образом, чтобы рассчитать индекс цен, необходимо сопоставить стоимость товаров, проданных в текущем периоде по ценам текущего периода со стоимостью этих же товаров, но по ценам базисного периода.

Агрегатный индекс физического объема товарооборота

Если индексируемой величиной являются количества (объемы) проданных или произведенных товаров, то для того, чтобы можно было суммировать их по разным товарам – необходимо ввести в индекс количеств соизмеритель в виде цен на продукты, т.е. соизмерить количества по ценам.

Произведение количеств на цены даст стоимость (или оборот по продаже), т.е. величины, которые можно суммировать.
Следовательно, в индексах физического объема продукции, цены являются весами. Эти веса должны быть взяты одинаковыми (неизменными) для текущего и базисного периодов. В этом случае индексы отразят только изменение объемов произведенных или проданных товаров.

Таким образом, и в индексе цен, и в индексе физического объема товарооборота при помощи соизмерителей мы переходим к стоимости проданных (произведенных) товаров.

При построении и исчислении индекса физического объема товарооборота возникает вопрос: какие цены взять в качестве соизмерителя (веса)? Цены базисного, или цены текущего периода?

Чтобы агрегатный индекс характеризовал только изменение физического объема и не отражал изменения цен, в качестве весов надо взять постоянные цены как для базисного, так и для текущего периодов.

Тогда формулу агрегатного индекса физического объема продукции можно представить следующим образом:

Выбор периода взвешивания индексов объясняется тем, что качественные индексируемые показатели не требуют соизмерения и их сомножители являются только весами, а количественные – требуют соизмерения и их сомножители являются соизмерителями.

Числитель индекса представляет собой стоимость продукции текущего периода в базисных ценах, знаменатель – стоимость продукции базисного периода в ценах базисного периода. Разность между числителем и знаменателем (∑q1p0 — ∑q0p0) характеризует абсолютное изменение физического объема продукции в текущем периоде.

Источник

ОБЩИЕ ИНДЕКСЫ

Общие, или сводные, индексы — это индексы, рассчитываемые для совокупности явлений. Изучаемые с помощью этих индексов явления могут быть сложными, имеющими неоднородный характер составляющих их элементов, подверженными влиянию сразу нескольких признаков-факторов.

Поэтому данный вид индексов является эффективным инструментом для обобщающего анализа социально-экономических явлений.

Общие индексы — это относительные показатели, характеризующие соотношения между такими совокупностями величин экономических явлений, которые непосредственно в своей натуральной форме несоизмеримы.

Общий индекс может быть групповым, если он рассчитывается не для всей совокупности, а лишь для части ее однородных элементов, объединенных в группу.

Общий индекс может рассчитываться по формулам агрегатного, среднего арифметического и среднего гармонического индексов.

Агрегатная форма общих индексов является основной в экономике- статистических расчетах, когда возникает необходимость провести анализ изменения цен не по одному товару, а по разнообразному ассортименту товаров, изменению объема проданного количества многих различных товаров и т.п.

Придерживаясь принятых обозначений, общее изменение товарооборота стоимости проданных товаров можно определить, сопоставив общую стоимость проданных товаров в отчетном периоде по ценам отчетного периода с общей стоимостью проданных товаров в базисном периоде по ценам базисного периода по формуле общего индекса товарооборота:

Аналогично индексу товарооборота рассчитываются индексы выпуска продукции, потребления, численности работников, издержек обращения и т.д.

Агрегатные индексы — это индексы, числители и знаменатели которых представляют собой суммы, произведения или суммы произведений уровней изучаемого явления:

Агрегатная форма индексов показывает относительное изменение изучаемого экономического явления и абсолютные размеры этого изменения.

Чтобы определить абсолютное фактическое изменение товарооборота, необходимо из числителя формулы индекса товарооборота вычесть знаменатель:

Веса агрегатных индексов используются для оценки роли отдельных факторов, образующих сложное явление, и представляют собой величины, при помощи которых несоизмеримые показатели индекса приводятся в сопоставимый вид.

В условиях рыночных отношений в экономике особое место среди индексов качественных показателей отводится индексу потребительских цен. С помощью индекса потребительских цен оценивается динамика цен на товары производственного и непроизводственного потребления, пересчитываются важнейшие стоимостные показатели в сопоставимые цены, измеряется инфляция и т.д.

где — условная стоимость товаров, реализованных в отчетном

периоде по ценам базисного периода.

Исчисленный по этой формуле общий индекс цен показывает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализованного в отчетном периоде по сравнению с базисным периодом. Такое построение индекса принято называть построением Пааше.

Однако в условиях экономического кризиса резко растут цены. В результате ряд товаров выпадает из потребления населения, особенно малообеспеченного. В этих условиях более правильно отразить изменение цен (индекс цен) по формуле Ласпейреса, где в качестве весов берется неизменное количество товара за базисный период:

Этот индекс показывает, насколько изменились цены в отчетном периоде по сравнению с базисным по тем товарам, которые были реализованы в базисном периоде, и экономию, которую можно было получить от изменения цен, т.е. условную экономию. Иначе говоря, индекс Ласпейреса показывает, во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде.

Индекс цен позволяет определить и абсолютную величину экономии, полученную от снижения цен (если результат со знаком «—») или перерасхода (если результат со знаком «+») как разность между числителем и знаменателем формул индекса цены:

В статистике более употребительным является индекс цен с весами текущего периода (по формуле Пааше), поскольку больший экономический смысл имеет выявление изменения цен на товары, реализованные в текущем периоде, а не на те, которые были проданы в прошлом периоде.

Агрегатный индекс физического объема характеризует изменение количества проданных товаров не в денежных, а в физических (натуральных) единицах измерения, где в качестве весов (соизмерите- лей) по формуле Пааше берется цена товаров в отчетном периоде:

Полученный индекс физического объема показывает изменение только количества проданных товаров по ценам отчетного периода.

По формуле Ласпейреса при исчислении агрегатного индекса физического объема в качестве весов берется неизменная цена товара на уровне базисного периода:

Более употребительным является индекс физического объема с весами базисного периода (по формуле Ласпейреса), потому что большее значение имеет выявление изменения количества товаров,

реализованных в текущем периоде по ценам начальным, а не то количество товаров, которое было продано по повышенным ценам текущего периода.

Индекс физического объема также позволяет определить абсолютную величину изменения количества реализованных товаров как разность числителя и знаменателя формул индекса:

Индексы связанных между собой показателей называются сопряженными.

Абсолютное изменение товарооборота за счет изменения одного фактора — цены (Ар) или физического объема продукции (Aq) — называется частным абсолютным изменением товарооборота.

Абсолютное изменение товарооборота за счет двух факторов (ценностного и количественного) называется общим изменением товарооборота.

Частные и общее изменения товарооборота взаимосвязаны между собой: Ар + Aq = Apq, что позволяет проверить правильность выполненных расчетов.

Агрегатный индекс себестоимости характеризует уровень себестоимости нескольких видов продукции, выпускаемых предприятием, причем себестоимость взвешивается по объему производства отдельных видов продукции текущего периода:

Числитель этого индекса отражает затраты на производство текущего периода, а знаменатель — условную величину затрат при сохранении себестоимости на базисном уровне.

Разность числителя и знаменателя показывает сумму экономии предприятия от снижения себестоимости:

Индекс затрат на производство, взвешенный по себестоимости, имеет следующий вид:

Абсолютное изменение затрат на производство за счет двух факторов — изменения себестоимости и физического объема — определяется аналогичным образом:

Указанные индексы (/, I_q, /_ад) являются сопряженными и также взаимосвязаны между собой: I_z I_q = I _zq

Агрегатный индекс производительности труда и агрегатный индекс трудоемкости взаимосвязаны между собой, так как производительность труда является обратным показателем трудоемкости, т.е. количество продукции, вырабатываемое в единицу времени (в натуральном выражении), и затраты времени на единицу продукции можно представить формулой

Следовательно, снижение трудоемкости в отчетном периоде по сравнению с базисным свидетельствует о росте производительности труда.

Агрегатный индекс трудоемкости:

Агрегатный индекс производительности труда:

Числитель данного индекса представляет собой условную величину, показывающую, какими были бы затраты времени на выпуск продукции, если бы трудоемкость не изменилась, а знаменатель отражает реально имевшие место затраты времени на выпуск всей продукции в текущем периоде.

Индекс производительности труда по трудоемкости связан

с индексом затрат рабочего времени (труда) (1_Т) и с индексом физического объема продукции, взвешенным по трудоемкости (I_q):

где

Индексы средние из индивидуальных — это форма индексов, вычисленных как средние арифметические или средние гармонические.

Любой общий индекс можно представить как среднюю взвешенную из индивидуальных индексов. Однако при этом форму средней выбирают таким образом, чтобы полученный средний индекс был тождествен исходному агрегатному индексу.

Если стоимость проданной продукции в текущем периоде составляет величину р_х q_v индивидуальные индексы цен , тогда в

знаменателе формулы агрегатного индекса цен можно

Таким образом, общий индекс цен будет выражен в форме средней гармонической из индивидуальных индексов:

Абсолютное изменение товарооборота определяется как разность между числителем и знаменателем формулы:

Источник