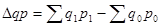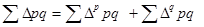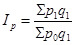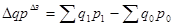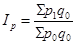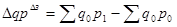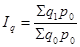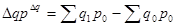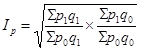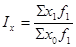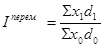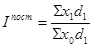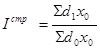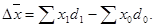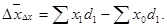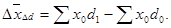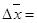общий индекс стоимости продукции
Расчет индекса цен: примеры, формулы, онлайн-калькулятор
Быстрая навигация по странице:
Система индексов цен
Контроль цен имеет важное значение в экономике. Комплекс показателей статистики цен состоит их широкого спектра критериев, позволяющих изучить различные аспекты величины, изменения и структуры стоимости товаров и услуг. В процессе исследования изучаются розничные цены и тарифы, оптовые, отпускные, закупочные, сметные, мировые и другие виды цен. Одним из важнейших инструментов такого анализа выступают различные индексы цен: Ласпейреса и Пааше, агрегатные и средние из индивидуальных, Фишера и т.п. Изменение средних цен исследуется посредством системы следующих индексов: переменного состава, постоянного состава и структурных сдвигов (данные показатели взаимосвязаны). В целом рассчитываемые показатели являются относительными, которые отражают соотношение уровней какого-либо явления во времени или в пространстве и позволяет выполнить сравнение фактических значений с эталонными, плановыми, прогнозными и т.п. величинами. По степени охвата рассматриваемые показатели могут быть как индивидуальными (при расчете, например, для конкретного товара), так и сводными (при расчете значений, например, по группе товаров). По базе сравнения рассматриваемые показатели относятся к динамическим (например, при анализе изменения стоимости набора продуктов питания за различные периоды времени), но могут рассчитываться и территориальные значения. По форме построения рассматриваемые показатели могут быть как агрегатными, так и средними.
Размещено на www.rnz.ru
Формула индекса цен
В зависимости от вида индекса можно использовать несколько формул, позволяющих вычислить индекс цен. Так, при расчете индивидуальных индексов используют следующую формулу:

Для расчета значения сводного (общего, агрегатного) индекса цен применяется формула Пааше:

В силу специфики правового регулирования индекс потребительских цен в РФ рассчитывается на основе формулы Ласпейреса (Ласпейраса):

Модифицированная формула, применяемая для практических вычислений при проведении статистического наблюдения, приводится в Приказе Росстата от 30.12.2014 N 734 «Об утверждении Официальной статистической методологии организации статистического наблюдения за потребительскими ценами на товары и услуги и расчета индексов потребительских цен».
Пример расчета индекса цен
Исходные данные: имеется следующая информация о реализации товаров предприятиями города:
| Продукция | Базисный период | Отчетный период | ||
|---|---|---|---|---|
| Стоимость единицы, руб. | Количество, шт. | Стоимость единицы, руб. | Количество, шт. | |
| Товар №1 | 25 | 15 | 22 | 17 |
| Товар №2 | 18 | 24 | 19 | 25 |
| Товар №3 | 16 | 45 | 18 | 44 |
На основе исходных данных определить индивидуальные и общий индекс цен, индекс потребительских цен, потери покупателей от роста цен (или экономию в случае их снижения).
Составим таблицу вспомогательных расчетов:
Вычислим индивидуальные индексы цен:
Общий (агрегатный) индекс цен рассчитаем по формуле Пааше:
Индекс потребительских цен рассчитаем по формуле Ласпейреса:
Ip = ∑p1q0 : ∑p0q0 = 1596 / 1527 = 1,045. Полученное значение индекса показывает, что уровень потребительской инфляции по рассматриваемой группе товаров составил 4,5%.
Онлайн калькулятор индекса цен
Для вычисления агрегатного индекса цен и индекса потребительских цен приводим простую форму онлайн-калькулятора, используя который, Вы можете самостоятельно выполнить расчет данных показателей и заполнить таблицу. Для получения правильных результатов работы онлайн-калькулятора в процессе ввода данных необходимо внимательно соблюдать размерность полей, что позволит выполнить необходимые вычисления быстро и точно. Дробные величины должны вводиться с ТОЧКОЙ, а не с запятой! В представленной форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает расчет индекса потребительских цен онлайн. Для вычисления указанных показателей по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет».
Общие индексы



Индекс стоимости продукции:
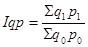
Индекс показывает во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным за счет изменения цен на товары и объемов их производства и реализации или сколько процентов составляет рост (снижение) стоимости продукции.
Разница между числителем и знаменателем индекса составляет абсолютное изменение стоимости продукции (прирост или снижение) за счет совместного действия двух факторов: цен на продукцию и ее количества.
Абсолютное изменение произошло под влиянием факторов:
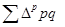
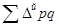
Изменение индекса стоимости продукции зависит от двух факторов: цены и физического объема.
Индекс цен Пааше (по отчетным весам):
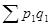
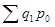
Общий индекс цен показывает, во сколько раз возросла (уменьшилась) стоимость продукции в отчетном периоде по сравнению с базисным периодом в результате изменения цен.
Разница между числителем и знаменателем индекса показывает, на сколько денежных единиц изменилась стоимость продукции в результате изменения цен или на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.
Индекс цен Ласпейреса:
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по той продукции, которая была реализована в базисном периоде, и экономию (перерасход), которую можно было бы получить от изменения цен, т.е. условную экономию (перерасход). Т.е. он показывает, во сколько раз товары базисного периода подорожали (подешевели) из-за изменения цен на них в отчетном периоде.
Разница между числителем и знаменателем индекса показывает, на сколько денежных единиц товары в базисном периоде стали дороже дешевле) из-за изменения цен на них в отчетном периоде.
Индекс физического объема (и любых количественных показателей):
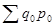
Индекс физического объема продукции показывает, во сколько раз изменилась стоимость продукции в отчетном периоде по сравнению с базисным периодом в результате изменения физического объема ее производства.
Разница между числителем и знаменателем индекса означает абсолютное изменение стоимости продукции (прирост или снижение) за счет изменения только физического объема производства продукции.
Индекс цен Фишера («Идеальная» формула Фишера):
Средняя величина, является характеристикой качественного показателя и складывается под влиянием значений показателя у отдельных единиц, из которых состоит объект, но и под влиянием соотношения их весов (структуры).
Динамику среднего показателя можно отразить как за счет изменения обоих факторов, так и за счет каждого фактора отдельно. Для этого используются индексы переменного состава, постоянного состава и структурных сдвигов.
Индекс переменного составапредставляет собой отношение двух взвешенных средних величин с изменяющимися (переменными) весами, которые показывают изменение индексируемой величины:
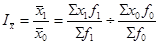
где х – индексируемые величины;
Индекс переменного состава отражает динамику среднего показателя за счет изменения индексируемой величины и за счет изменения весов, по которым взвешиваются отдельные значения.
Индекс переменного состава состоит из двух сомножителей: индекса постоянного состава и индекса структурных сдвигов.
Индекс постоянного (фиксированного) состава:
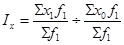
Индекс постоянного состава отражает динамику среднего показателя лишь за счет изменения индексируемой величины при фиксированном весе.
Индекс структуры (структурных сдвигов):
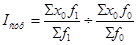
Индекс структурных сдвигов отражает динамику среднего показателя за счет изменения весов.
Между индексами существует взаимосвязь:
В качестве весов индексов средних величин могут быть использованы и относительные показатели (доли) d.
где d1, d0 – доли единиц с определенным значением признака в общей совокупности в отчетном и базисном периодах ∑d = 1.
Разница между числителем и знаменателем индекса переменного состава показывает абсолютное изменение среднего уровня признака как за счет изменения значений самого признака у отдельных единиц совокупности, так и за счет структурных изменений:
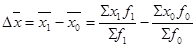
Разница между числителем и знаменателем индекса постоянного состава показывает абсолютное изменение среднего уровня признака за счет изменения значений самого признака у отдельных единиц совокупности:
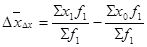
Разница между числителем и знаменателем индекса структурных сдвигов показывает абсолютное изменение среднего уровня признака за счет структурных изменений:
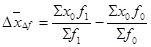
Совместное влияние факторов:
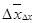
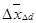
Общий индекс стоимости продукции (товарооборота)
Общий индекс стоимости продукции или товарооборота представляет собой отношение стоимости продукции текущего периода к стоимости продукции в базисном периоде.
Индекс показывает, как изменилась стоимость продукции (товарооборота) отчетного периода по сравнению с базисным или сколько процентов составляет динамика стоимости продукции. Если из значения индекса стоимости вычесть 100 %, то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Разность числителя и знаменателя показывает, на сколько рублей изменилась стоимость продукции в текущем периоде по сравнению с базисным.
Аналогично строятся индексы для показателей, которые являются произведением двух сомножителей: затраты на производство продукции (произведение себестоимости единицы продукции на количество продукции); затрат времени на производство всей продукции (произведение затрат времена на производство единицы продукции на количество выработанной продукции).
Решение типовой задачи
Рассмотрим расчет взаимосвязанных индексов физического объема, цен и стоимости продукции на условном примере.
Таблица 18 – Показатели деятельности предприятия
| Вид продукции | Объем производства продукции в натуральном выражении | Цена единицы, руб. | |
| январь | февраль | январь | февраль |
| q0 | q1 | p0 | p1 |
| А, штук | |||
| В, кг |
1) индивидуальные индексы физического объема, цен и стоимости произведенной продукции;
2) общий индекс физического объема продукции и изменение стоимости продукции в феврале за счет снижения объемов производства;
3) общий индекс цен и изменение в феврале стоимости продукции за счет за счет повышения цен;
4) общий индекс стоимости произведенной продукции и изменение стоимости продукции в феврале за счет совместного влияния обоих факторов;
5) взаимосвязь между индексами и между абсолютными изменениями стоимости продукции.
Индивидуальные индексы по видам продукции рассчитаем в таблице:
Таблица 19 – Индивидуальные индексы по видам продукции
| Индивидуальные индексы | Продукция «А» | Продукция «В» |
| Физического объема | 0,900 | 0,950 |
| Цен | 1,100 | 1,250 |
| Стоимости продукции | 0,990 | 1,187 |
Пример расчета показателей по продукции «А»:
1. Индивидуальный индекс физического объема

2. Индивидуальный индекс цен

3. Индивидуальный индекс стоимости продукции (товарооборота)
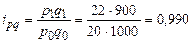
Покажем взаимосвязь между индексами:
по продукции «А» 
Таблица 20 – Определение стоимости продукции (товарооборота)
| Вид продукции | Январь | Февраль | В феврале по ценам января |
p0q0  | p1q1 | p0q1 | |
| А | 20,0 | 19,8 | 18,0 |
| В | 32,0 | 38,0 | 30,4 |
| Всего | 52,0 | 57,8 | 48,4 |
2) общий индекс физического объема продукции


Стоимость продукции в феврале по сравнению с январем уменьшилось на 6,9 % (93,1 – 100) или на 3,6 тыс. руб. (48,4 – 52,0) за счет изменения количества произведенной продукции.
3) общий индекс цен


4) общий индекс стоимости продукции (товарооборота)
В феврале по сравнению с январем стоимость продукции увеличилась на 5,8 тыс. руб. (57,8 – 52,0) или на 11,2 % (111,2 – 100).
— между общими индексами:

— между абсолютными изменениями стоимости произведенной продукции:

Индексы средних величин
Индексный метод широко применяется для изучения динамики средних величин качественных показателей и выявления факторов, влияющих на динамику средних. В этом случае исчисляется система взаимосвязанных индексов:
Индекс переменного состава
Индекс переменного состава представляет собой отношение двух взвешенных средних величин, характеризующих общее изменение индексируемого осредняемого показателя (x).
Индекс переменного состава для любых качественных показателей имеет вид:
Величина этого индекса характеризует общее изменение средней величины показателя за счет влияния двух факторов:
1) осредняемого показателя у отдельных единиц совокупности (xi)
2) структуры изучаемой совокупности ( 
Индекс структурных сдвигов
Индекс структурных сдвигов характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня изучаемого показателя и рассчитывается по формуле:
Индекс фиксированного состава
Индекс фиксированного состава показывает, как изменилась средняя величина изучаемого показателя только за счет изменения осредняемого показателя у отдельных единиц совокупности. В общем виде он может быть записан так:
Индекс переменного состава представляет собой произведение двух индексов-сомножителей: индекса фиксированного состава и индекса структурных сдвигов.

Аналогично приведенным формулам строятся индексы средних показателей: цен, себестоимости единицы продукции, заработной платы, производительности труда, фондоотдачи и т.п.
Средние индексы
Помимо агрегатных индексов в статистике применяется другая форма – средневзвешенные индексы. К их исчислению прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Для этого индексируемая величина отчётного периода, стоящая в числителе агрегатного индекса, заменяется произведением индивидуального индекса на индексируемую величину базисного периода.
Средний арифметический индекс физического объема продукции вычисляется по формуле
т.к. индивидуальный индекс физического объема 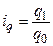
Средний геометрический индекс цен вычисляется по формуле
т.к. индивидуальный индекс цен 
Решение типовой задачи
Таблица 21 – Показатели реализации продукции на предприятии
| Товар | Выручка от продажи в отчетном периоде, тыс. руб. | Изменение цен в отчетном периоде по сравнению с базисным, % |
| А | +4 | |
| Б | +16 |
1) Общий индекс цен
2) Общий индекс физического объема при условии, что товарооборот в отчетном периоде увеличился на 5,3%.
1) Определим общий индекс цен
Согласно исходным данным, для расчета индекса имеются данные о величине товарооборота в отчетном периоде ( 

Товарооборот(выручка от продажи) в отчетном периоде по сравнению с базисным увеличился на 10,1 % (1,101·100 – 100 = 10,1%) или на 125 тыс.руб. (1365– 1240) за счет изменения цен на продукцию.
2) Определим общий индекс физического объема исходя из взаимосвязи между индексами.

Товарооборот снизился на 4,4 % (0,956·100 – 100 = – 4,4%) за счет изменения количества проданной продукции.