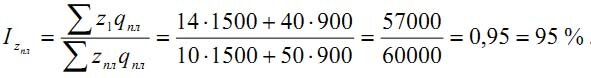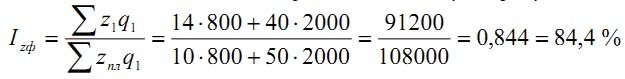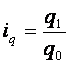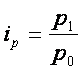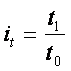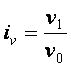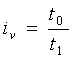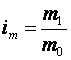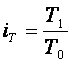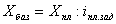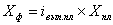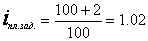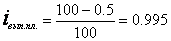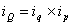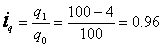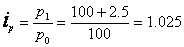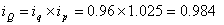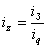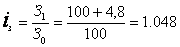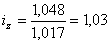общий индекс планового задания

Индексы выполнения плана

Особенность таких индексов заключается в том, что при их вычислении фактические данные сопоставляются не с базисными, а с плановыми. Причем, весами индекса могут быть как плановые показатели, так и фактические.

НАПРИМЕР, имеются следующие данные.
Таблица 2 Количество и себестоимость продукции, выпущенной заводом

Выпущено продукции, Единиц

Себестоимость единицы проду к ции, грн.

По данным таблицы можно рассчитать индексы с плановыми и фактическими весами:

Таким образом, себестоимость запланированной к выпуску продукции ниже плановой себестоимости на 5 %.
Если же в качестве веса взять фактический выпуск продукции, то получим:

Этот индекс показывает, что себестоимость фактически выпущенной продукции ниже плановой на 15,6 %.

Первый индекс с плановыми весами характеризует выполнение плана по себестоимости запланированной к выпуску продукции (выпуск которой предусмотрен был планом). Здесь в качестве веса принято плановое задание. Однако предприятия иногда нарушают ассортимент выпускаемой продукции, предусмотренной планом, по разным причинам. Поэтому для определения себестоимости фактически произведенной продукции, по сравнению с плановой себестоимостью, в качестве весов могут быть приняты не плановый, а фактический выпуск продукции.

Этот индекс рассчитывается как отношение фактических затрат на фактически произведенную продукцию к плановым затратам на эту же продукцию.

Источник

Абсолютные и относительные статистические величины

Понятие абсолютных величин

Абсолютные величины — это результаты статистических наблюдений. В статистике в отличие от математики все абсолютные величины имеют размерность (единицу измерения), а также могут быть положительными и отрицательными.

Единицы измерения абсолютных величин отражают свойства единиц статистической совокупности и могут быть простыми, отражая 1 свойство (например, масса груза измеряется в тоннах) или сложными, отражая несколько взаимосвязанных свойств (например, тонно-километр или киловатт-час).

Единицы измерения абсолютных величин могут быть 3 видов:

Абсолютные величины могут быть моментными или интервальными. Моментные абсолютные величины показывают уровень изучаемого явления или процесса на определенный момент времени или дату (например, количество денег в кармане или стоимость основных фондов на первое число месяца). Интервальные абсолютные величины — это итоговый накопленный результат за определенный период (интервал) времени (например, зарплата за месяц, квартал или год). Интервальные абсолютные величины, в отличие от моментных, допускают последующее суммирование.

Абсолютная статистическая величина обозначается X, а их общее число в статистической совокупности — N.

Количество величин с одинаковым значением признака обозначается f и называется частота (повторяемость, встречаемость).

Cами по себе абсолютные статистические величины не дают полного представления об изучаемом явлении, так как не показывают его динамику, структуру, соотношение между частями. Для этих целей служат относительные статистические величины.

Понятие и виды относительных величин

Относительная статистическая величина — это результат соотношения двух абсолютных статистических величин.

Если соотносятся абсолютные величины с одинаковой размерностью, то получаемая относительная величина будет безразмерной (размерность сократится) и носит название коэффициент.

Часто применяется искусственная размерность коэффициентов. Она получается путем их умножения:

Искусственная размерность коэффициентов применяется, как правило, в разговорной речи и при формулировании результатов, а в самих расчетах она не используется. Чаще всего применяются проценты, в которых принято выражать полученные значения относительных величин.

Чаще вместо названия относительная статистическая величина используется более краткий термин-синоним — индекс (от лат. index — показатель, коэффициент).

В зависимости от видов соотносимых абсолютных величин при расчете относительных величин, получаются разные виды индексов: динамики, планового задания, выполнения плана, структуры, координации, сравнения, интенсивности.

Индекс динамики

Индекс динамики (коэффициент роста, темп роста) показывает во сколько раз изменилось изучаемое явление или процесс во времени. Рассчитывается как отношение значения абсолютной величины в отчетный (анализируемый) период или момент времени к базисному (предыдущему):

.

Здесь и далее подиндексы означают: 1 — отчетный (анализируемый) период, 0 — базисный (прошлый) период.

Индекс планового задания

Индекс планового задания – это отношение планового значения абсолютной величины к базисному:

Например, автосалон в январе продал 100 автомобилей, а на февраль запланировал продать 120 автомобилей. Тогда индекс планового задания составит i пз = 120/100 = 1,2, что означает планирование роста продаж в 1,2 раза или на 20%

Индекс выполнения плана

Индекс выполнения плана – это отношение фактически полученного значения абсолютной величины в отчетном периоде к запланированному:

Например, автосалон в феврале продал 110 автомобилей, хотя на февраль было запланировано продать 120 автомобилей. Тогда индекс выполнения плана составит i вп = 110/120 = 0,917, что означает выполнение плана на 91,7%, то есть план недовыполнен на (100%-91,7%) = 8,3%.

Перемножая индексы планового задания и выполнения плана, получим индекс динамики:

В рассмотренном ранее примере про автосалон, если перемножим полученные значения индексов планового задания и выполнения плана, то получим значение индекса динамики: 1,2*0,917 = 1,1.

Индекс структуры

Индекс структуры показывает, какую долю составляет отдельная часть совокупности от всей совокупности.

Например, если в рассматриваемой группе студентов 20 девушек и 10 молодых людей, тогда индекс стурктуры (доля) девушек будет равен 20/(20+10) = 0,667, то есть доля девушек в группе составляет 66,7%.

Индекс координации

Индекс координации показывает, во сколько раз больше или сколько процентов составляет одна часть статистической совокупности по сравнению с другой ее частью, принятой за базу сравнения.

Например, если в группе студентов из 20 девушек и 10 молодых людей, принять за базу сравнения численность девушек, тогда индекс координации численности молодых людей составит 10/20 = 0,5, то есть численность молодых людей составляет 50% от численности девушек в группе.

Индекс сравнения

где А, Б — признаки сравниваемых объектов или территорий.

Индекс интенсивности

Например, хлебный магазин продал 500 буханок хлеба и заработал на этом 10000 руб., тогда индекс интенсивности составит 10000/500 = 20 [руб./бух.хлеба], то есть цена продажи хлеба составила 20 руб. за буханку.

Большинство величин с дробной размерностью представляют собой индексы интенсивности.

Источник

Высшая математика и экономика

Образовательные онлайн сервисы: теория и практика

Математика в экономике. Экономическая статистика

Абсолютные и относительные статистические величины

Задача 1. Расход топлива на производственные нужды предприятия характеризуется в отчетном периоде следующими данными:

Теплотворная способность, МДж/кГ

Определить общее количество потребленного условного топлива (1 т.у.т. = 29,3 МДж/кГ) по плану и фактически, а также процент выполнения плана по общему расходу топлива.

Решение. Учитывая стандартную теплотворную способность 29,3 МДж/кГ, определяем количество потребленного условного топлива каждого вида по плану (X’1i) и фактически (X1i):

дизельное топливо: X1дт = 41,9/29,3*1050 = 1501,536 т.у.т.;

мазут: X1м = 40,1/29,3*730 = 999,078 т.у.т.;

уголь: X1у = 26,4/29,3*555 = 500,068 т.у.т.
Суммируя количество потребленного условного топлива каждого вида, получим общее количество потребленного условного топлива:

Для определения процента выполнения плана необходимо рассчитать индекс выполнения плана, то есть отношение значений по факту и плану отчетного периода:
,
= 3000,682/2906,997 = 1,032, то есть план по общему расходу топлива перевыполнен на 3,2%.

Задача 2. Рассчитать индекс и темп изменения, если в марте произведено продукции 130 тонн, а в феврале 100 тонн. Решение. Индекс изменения (динамики) характеризует изменение какого-либо явления во времени. Он представляет собой отношение значений одной и той же абсолютной величины в разные периоды времени. Данный индекс определяется по формуле:
,
где подиндексы означают: 1 — отчетный или анализируемый период, 0 — прошлый или базисный период.
Критериальным значением индекса динамики (темпа роста) служит единица, то есть если >1, то имеет место рост явления во времени; если =1 – стабильность; если 1 – рост объема произведенной продукции.
Темп изменения (прироста) определяется по формуле:
.
Т = 1,3 – 1 = 0,3 (или 30%), то есть объем произведенной продукции вырос в марте по сравнению с февралем на 30%.

Задача 3. Рассчитать индексы планового задания, выполнения плана и динамики, если выпуск продукции в отчетном году составил 100 млн. рублей, на следующий год планировалось 140 млн. рублей, а фактически получено 112 млн. рублей. Решение. Индекс планового задания – это отношение значений одной и той же абсолютной величины по плану анализируемого периода и по факту базисного. Он определяется по формуле:
,
где X’1 — план анализируемого периода; X0 — факт базисного периода.
Применяя формулу (4) имеем: = 140/100 = 1,4 (или 140%), то есть на следующий год планировалось выпустить продукции в размере 140% от объема предыдущего года.
Индекс выполнения плана определим: = 112/140 = 0,8 (или 80%), то есть план по увеличению выпуска продукции выполнили лишь на 80% или недовыполнили на 20%.
Индекс динамики можно определить по формуле (2) или перемножая индексы планового задания и выполнения плана, то есть = 1,12.

Задача 4. Суммарные денежные доходы россиян в 2005 г. составили 13522,5 млрд. руб., из которых 8766,7 млрд. руб. составила оплата труда, 1748,4 млрд. руб. – социальные выплаты, 1541,7 млрд. руб. – доход от предпринимательской деятельности, 1201,5 млрд. руб. – доходы от собственности, остальное – прочие доходы. Рассчитать относительные величины структуры и координации, приняв за основу оплату труда. Построить секторную (круговую) диаграмму структуры доходов. Решение. Индекс структуры (доля) – это отношение какой-либо части величины (совокупности) ко всему ее значению. Он определяется по формуле:

Применяя формулу (5) и округляя значения до 3-х знаков после запятой, имеем:

Долю прочих доходов найдем, используя формулу (6), согласно которой сумма всех долей равна единице:
.
Таким образом, доля прочих доходов dпроч = 1 – 0,648 – 0,129 – 0,114 – 0,089 = 0,020 или 2,0%.
Для иллюстрации структуры (составных частей) доходов построим секторную диаграмму (рис.1):

Рис.1. Структура денежных доходов населения РФ в 2005 году.
Таким образом, очевидно, что наибольшую долю в суммарных денежных доходах составляет оплата труда (64,8%), на 2-м месте – социальные выплаты (12,9%), затем следуют предпринимательский доход (11,4%), доходы от собственности (8,9%), а прочие доходы составляют лишь 2%.
Индекс координации – это отношение какой-либо части величины к другой ее части, принятой за основу (базу сравнения). Он определяется по формуле:
.
индекс координации социальных выплат = 1748,4/8766,7 ≈ 0,129/0,648 = 0,199;

Таким образом, социальные выплаты составляют 19,9% от оплаты труда, предпринимательский доход – 17,6%, доходы от собственности – 13,7%, а прочие доходы – 3,1%.

Задача 5.Запасы воды в озере Байкал составляют 23000 км3, а в Ладожском озере 911 км3. Рассчитать относительные величины сравнения запасов воды этих озер. Решение. Индекс сравнения – это отношение значений одной и той же величины в одном периоде или моменте времени, но для разных объектов или территорий. Он определяется по формуле:
,
где А, Б — признаки сравниваемых объектов или территорий.
Применяя формулу и принимая за объекты А и Б, соответственно, озера Байкал и Ладожское, найдем индекс сравнения: = 23000/911 = 25,25, то есть запасов воды в озере Байкал в 25,25 раза больше, чем в Ладожском озере.
Меняя базу сравнения, найдем индекс сравнения Ладожского озера с Байкалом по той же формуле: = 911/23000 = 0,0396 или 3,96%, то есть запасы воды в Ладожском озере составляют 3,96% запасов воды в озере Байкал.

Источник

Общий индекс планового задания

— область применения и методику расчёта индивидуальных индексов;

— исчислить индивидуальные индексы количественных и качественных показателей;

— формулировать вывод по полученным результатам.

Индексы – это относительные величины сравнения сложных статистических совокупностей или их отдельных единиц. Индекс представляет собой относительный показатель, выражающий соотношение величин какого – либо явления во времени, в пространстве, или же сравнение фактических данных с любым эталоном (планом, прогнозом, нормативом и т.д.).

На практике индивидуальные (частные) индексы принято обозначать символом i (начальная буква латинского слова index ). Знак внизу справа у индексируемого показателя означает период: 0 –базисный, 1 – отчётный, или же уровень показателя: пл – плановый, ф – фактический, н – нормативный. Помимо этого используются определённые символы для обозначения индексируемых показателей:

Символ для обозначения индексируемого показателя

Физический объём продукции (товара) в натуральном выражении

Цена единицы продукции (товара)

Себестоимость единицы продукции

Затраты времени на производство единицы продукции

Выработка продукции в натуральном выражении на одного рабочего или в единицу времени

Удельный расход материала

Выработка продукции в стоимостном выражении на одного рабочего или в единицу времени

Общие затраты времени на производство продукции (Т= t × q ) или численность рабочих (или персонала)

Стоимость продукции определённого наименования, или товарооборот

Издержки производства продукции определённого наименования

Индивидуальными называются индексы, которые отражают результат сравнения однотоварных явлений, т.е. они характеризуют изменение отдельных элементов сложного явления.

По базе сравнения индивидуальные индексы можно разделить на две группы: динамические и территориальные. Динамические индексы отражают изменение явлений во времени. Например, индекс цен изделий отдельных наименований в 2009 году по сравнению с предыдущим годом; индекс физического объёма производства изделий отдельных наименований в апреле по сравнению с мартом текущего года. Динамические индексы бывают базисные и цепные. Территориальные индексы применяются для межрегиональных сравнений: например, индекс цен на бензин марки АИ 92 в Москве по сравнению с Красноярском.

По объекту исследования индивидуальные индексы можно подразделить на индексы : производительности труда, себестоимости, цен, физического объёма продукции, численности персонала и т.д.

По характеру объекта исследования индивидуальные индексы могут быть индексами количественных (объёмных) показателей и индексами качественных показателей. В основе такого деления индексов лежит вид индексируемой величины. Например, к количественным индексам относится индекс физического объёма продукции определённого наименования, а к качественным индексам – индекс цен на изделия определённых наименований.

Перечень и формулы расчёта индивидуальных индексов представим в таблице:

Что показывает индекс

Индивидуальный индекс физического объёма продукции

Во сколько раз возрос (или уменьшился) физический объём продукции в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс цен

Во сколько раз возросла (или уменьшилась) цена единицы продукции (товара) в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс себестоимости

Во сколько раз возросла (или уменьшилась) себестоимость единицы продукции (товара) в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс трудоёмкости

Во сколько раз возросла (или уменьшилась) трудоёмкость единицы продукции в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс выработки (производительности труда)

Во сколько раз возросла (или уменьшилась) производительность труда в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс выработки по трудовым затратам

Во сколько раз возросла (или уменьшилась) производительность труда в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс удельного расхода материала

Во сколько раз возрос (или уменьшился) удельный расход материала в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс стоимости продукции (какого-либо товара)

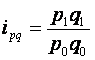
Во сколько раз возросла (или уменьшилась) стоимость продукции (какого- либо товара) в отчётном периоде по сравнению с базисным периодом

Индивидуальный индекс численности работников

Во сколько раз возросла (или уменьшилась) численность работников в отчётном периоде по сравнению с базисным периодом

Рассмотрим взаимосвязь следующих индексов:

Например: пусть имеются значения показателя Х за два периода

Базисный (предыдущий) период

Отчетный (текущий) период

Х_баз –ф актическое значение показателя в базисном периоде;

Индекс планового задания 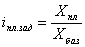(1) =>

Индекс выполнения плана 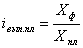(2) =>

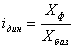
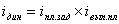
Индекс динамики (3)

(4)

т.е. произведение цепных индексов равно базисному индексу.

Планом промышленного предприятия предусматривалось увеличить физический объём продукции на 2% по сравнению с базисным периодом.

План выпуска продукции в натуральном исчислении недовыполнен на 0,5%.

Как изменился физический объём выпуска продукции в отчётном периоде по сравнению с базисным периодом?

Необходимо исчислить значение индекса динамики:

Индекс планового задания

Индекс выполнения плана

т е физический объём продукции в отчётном периоде вырос на 1,5% по сравнению с базисным периодом.

При расчёте индексов применяется следующее правило:

[Когда речь идёт об одноимённых индексах, то имеются в виду, например, индексы динамики.]

Пример : Как изменилась стоимость продукции «А», если физический объём продукции уменьшился на 4%, а цена выросла на 2,5% по сравнению с базисным периодом?

Стоимость продукции «А» можно представить в виде произведения физического

объёма продукции q на цену одной единицы продукции p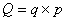

Аналогичное соотношение можно записать и для индексов динамики этих показателей:

Индекс динамики физического объёма продукции

Индекс динамики цены

Индекс динамики стоимости продукции

т.е. стоимость продукции «А» уменьшилась на 1,6% по сравнению с базисным периодом.

Ещё пример: Как изменилась себестоимость единицы продукции в отчётном периоде по сравнению с базисным периодом, если индекс физического объёма продукции составил 1,017, а сумма затрат на производство этой продукции выросла на 4,8%?

Себестоимость единицы продукции можно исчислить путём деления общей суммы затрат на производство на физический объём продукции :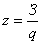

Аналогичное соотношение можно записать и для индексов динамики этих показателей:

Индекс динамики суммы затрат на производство

Индекс динамики физического объёма продукции задан условием i_q =1,017

Индекс динамики себестоимости единицы продукции

т.е. себестоимости единицы продукции увеличилась на 3% по сравнению с базисным периодом.

Источник