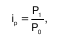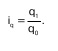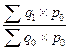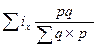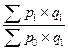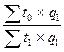общее понятие об индексах

Общее понятие об индексах

Особые формы записи индекса цен

Средние индексы и индексы средних показателей

Общие индексы

Индивидуальные индексы

Общее понятие об индексах

Статистическая наука имеет в своем арсенале метод, позволяющий соизмерить показатели какого-либо явления во времени и пространстве и сравнивать фактические данные с любым эталоном, в качестве которого может быть план, прогноз или какой-либо норматив. Это индексный метод, оперирующий с относительными показателями, в статистике называемыми индексами.

В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, исследуется роль отдельных факторов в формировании важнейших экономических показателей, индексы используются также в международных сопоставлениях экономических показателей, определении уровня жизни, мониторинге деловой активности в экономике и т.д.

Индекс (лат. index) — это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различия условий могут проявляться во времени (динамические индексы), в пространстве (территориальные индексы) и в выборе в качестве базы сравнения какого-либо условного уровня.

По охвату элементов совокупности (ее объектов, единиц и их признаков) различают индексы индивидуальные (элементарные) и сводные (сложные), которые, в свою очередь, делятся на общие и групповые.

В статистике под индексом понимается относительный показатель, который выражает соотношение величин какого-либо явления во времени, в пространстве, или сравнение фактических данных с любым эталоном.

С помощью индексов решаются следующие задачи:

· измерение динамики социально-экономического явления за два периода времени и более;

· измерение динамики среднего экономического показателя;

· измерение соотношения показателей по разным регионам;

· определение степени влияния изменений значений одних показателей на динамику других.

В международной практике индексы принято обозначать символами i и I (начальная буква латинского слова index). Буквой «i» обозначаются индивидуальные (частные) индексы, буквой «I» — общие индексы.

Помимо этого, используются определенные символы для обозначения показателей структуры индексов:

q — количество (объем) какого-либо товара в натуральном выражении;

р — цена единицы товара;

z — себестоимость единицы продукции;

t — затраты времени на производство единицы продукции;

w — выработка продукции в стоимостном выражении на одного рабочего или в единицу времени;

v — выработка продукции в натуральном выражении на одного рабочего или в единицу времени;

Т — общие затраты времени (tq) или численность рабочих;

рq — стоимость продукции или товарооборот;

zq — издержки производства.

Знак внизу справа от символа означает период: 0 — базисный; 1 — отчетный.

Все индексы можно классифицировать по следующим признакам:

· степень охвата явления;

· вид весов (соизмерителя);

По степени охвата явления индексы бывают индивидуальные и сводные (общие).

Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления. Например, изменение объема производства отдельных видов продукции (телевизоров, электроэнергии и т.д.), а также цен на акции какого-либо предприятия.

Сводные (сложные) индексы служат для измерения сложного явления, составные части которого непосредственно несоизмеримы. Например, изменения физического объема продукции, включающей разноименные товары, индекса цен акций предприятий региона и т.п.

По базе сравнения индексы бывают динамические и территориальные.

Динамические индексы служат для характеристики изменения явления во времени. Например, индекс цен на продукцию в 2010 г. по сравнению с предыдущим. При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий период, который называют базисным. Динамические индексы бывают базисные и цепные.

Территориальные индексы служат для межрегиональных сравнений. Используются, как правило, в международной статистике.

По виду весов индексы бывают с постоянными и переменными весами.

По форме построения различают агрегатные и средние индексы. Агрегатная форма является наиболее распространенной. Средние индексы являются производными от агрегатных.

По характеру объекта исследования индексы бывают производительности труда, себестоимости, физического объема продукции и т.п.

По составу явления индексы бывают постоянного (фиксированного) состава и переменного состава.

По периоду исчисления индексы бывают годовые, квартальные, месячные, недельные.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Общее понятие об индексах, их применение

В правовой статистике под индексомпонимают относительный показатель сравнения, характеризующий изменение (во времени, пространстве или по сравнению с любым эталоном) величины какого-либо явления (простого или сложного, состоящего из соизмеримых или несоизмеримых элементов).

Сфера применения индексов в аналитической практике очень широка: с их помощью характеризуется изменение правовых и юридически значимых явлений во времени – индексы динамики, в пространстве – территориальные индексы. С помощью индексов можно определить степень влияния отдельных факторов на изменение динамики сложного явления (например, влияние изменения числа отдельных видов преступлений и изменения структуры преступности на общее число преступлений) и т.д. Индексы позволяют проводить сравнения не только во времени и пространстве, но и с планами, нормативами, прогнозами.

Значения индексов выражают в коэффициентах или процентах. Если из полученного значения индекса, выраженного в процентах, вычесть 100%, то полученная разность покажет, на сколько процентов возросла (или сократилась) индексируемая величина.

В зависимости от степени охвата единиц изучаемой совокупности индексы подразделяются на индивидуальные и общие (сводные).

Индивидуальныминазываются индексы, характеризующие изменения отдельных элементов сложного явления (например, рост или снижение числа дорожно-транспортных происшествий).

Общими (сводными)называются индексы, характеризующие изменение всех элементов сложного явления, т.е. изменение во времени или в пространстве всего объема изучаемого явления (например, среднюю динамику совокупности преступлений, прямо не соизмеримых). В зависимости от целей исследования, характера индексируемых показателей и исходных данных построение общих индексов может осуществляться одним из двух способов: агрегатным и средневзвешенным из индивидуальных индексов. Средние индексы подразделяются в свою очередь на средние арифметические и на гармонические.

Агрегатные индексы являются основной формой индексов, применяемой в практической статистике многих стран мира. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируется), а другая – остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для соизмерения непосредственно несоизмеримых индексируемых величин. Умножение индексируемых величин на весы индексов принято называть взвешиванием. Агрегатные индексы могут быть рассчитаны как индексы переменного состава (сопоставляются показатели, рассчитанные на основе изменяющихся структур явлений) и индексы постоянного (фиксированного) состава (показатели сопоставляются на основе неизменной структуры явлений).

На основе различных взаимосвязей между правовыми явлениями может быть произведен индексный факторный анализ, позволяющий охарактеризовать как изменение отдельного юридически значимого явления в целом, так и его изменение под воздействием на него изменения различных факторов, определяющих развитие этого явления.

В уголовно-правовой статистике особый интерес представляют индексы тяжести преступлений, отражающие степень общественной тяжести различных преступлений, совершенных в различное время или на различных территориях.

Источник

Общее понятие об индексах и индексном методе

Индекс (лат. Index) – это относительная величина, показывающая, во сколько раз уровень изучаемого явления в данных условиях отличается от уровня того же явления в других условиях. Различие условий может проявляться во времени, в пространстве и в выборе в качестве базы сравнения какого-либо условного уровня.

По охвату элементов совокупности различают индексы индивидуальные и сводные, которые делятся на общие и групповые.

Индивидуальные индексы – это результат сравнения двух показателей, относящихся к одному объекту. В статистико-экономическом анализе деятельности предприятий и отраслей широко применяются индивидуальные индексы качественных и количественных показателей. Определяются по формуле:

Индекс цен характеризует относительное изменение уровня цены единицы каждого вида продукции в отчетном периоде по сравнению с базисным и является качественным показателем.

Индекс физического объема определяется по формуле:

Показатель, изменение которого характеризует индекс, называется индексируемым. Индексируемые показатели могут быть двоякого рода. Одни из них измеряют общий, суммарный размер (объем) того или иного явления и условно называются объемными, экстенсивными. Эти показатели получаются как итог непосредственного подсчета или суммирования и являются исходными, первичными.

Другие показатели измеряют уровень явления или признака в расчете на ту или иную единицу совокупности и условно называются качественными, интенсивными: выработка продукции в единицу времени (или на одного работника), затраты рабочего времени на единицу продукции, себестоимость единицы продукции и т. д. Эти показатели получаются путем деления объемных показателей, т. е. носят расчетный, вторичный характер. Они измеряют интенсивность, эффективность явления или процесса и, как правило, являются либо средними, либо относительными величинами.

Источник

Общее понятие об индексах и их классификация

Индексы используются для характеристики выполнения плана (например, плана по выпуску продукции (работ, услуг), снижению себестоимости продукции (работ, услуг), росту производительности труда), для изучения динамики (например, исследование изменения оптовых и розничных цен на отдельные виды товаров, объёма произведенной продукции (работ, услуг), реальных и номинальных доходов населения), для сравнения уровней социально-экономических явлений по территориям.

Индексы применяются также для изучения роли факторов, оказывающих влияние на изменение данного явления. Например, с помощью взаимосвязи индексов можно определить, в какой мере увеличение объёма продукции (работ, услуг) зависит от роста производительности труда и в какой мере от увеличения числа рабочих и служащих.

Как правило сопоставляемые показатели характеризуют явления, состоящие из разнородных качественных элементов, суммирование которых невозможно из-за их несоизмеримости. Например, предприятие выпускает несколько видов продукции и оказывает различные услуг. Получить общий объём выпущенной продукции и оказанных услуг, применяя только натуральные единицы измерения невозможно. В этом случае следует использовать метод соизмерения. В качестве соизмерителя может выступать цена, себестоимость, трудоемкость единицы продукции и ряд других показателей.

Способы построения индексов зависят от содержания изучаемых явлений, методологии расчета исходных статистических показателей и целей исследования. В основу классификации индексов можно положить следующие признаки: степень охвата элементов изучаемой совокупности, содержание и характер индексируемой величины, методология расчета.

i_q = q₁ : q₀ = 650 : 610 100 = 106,5 %

Сводный индекс выражает соотношение величин сложного экономического явления, состоящего из элементов непосредственно несоизмеримых. Сводный индекс обозначается буквой “I”. Сводный индекс характеризует изменение во времени, по сравнению с планом или в пространстве объема разнородной продукции, цен на различные товары, себестоимости ряда изделий, производительности труда по группе предприятий и т.д. Для получения сводного индекса не может быть применено непосредственное суммирование таких несоизмеримых величин для каждого из сравниваемых периодов и последующее соотношение этих сумм. Расчет сводного индекса на основе простой средней из индивидуальных индексов также не может быть применен, так как в такой средней не учитывается удельный вес каждого элемента во всей совокупности изучаемого явления. Основной формулой для расчета сводного индекса является агрегатная формула, в которой с помощью весов индекса несоизмеримые величины приводятся к соизмеримому виду. Например, индекс физического объёма продукции можно рассчитать по следующей формуле:

I_q =

Сводные индексы можно разделить на групповые и общие. Групповой индекс рассчитывается для группы элементов, входящих в общую совокупность. Например, индекс цен для товаров, входящих в какую-либо товарную группу (молоко и молочные продукты, аудио- и видеотехника и т.д.).Групповые индексы рассчитываются по обычным формулам сводных индексов. Общий индекс рассчитывается для всей совокупности элементов изучаемого явления. Общий индекс иногда употребляется как синоним понятия сводного индекса.

Для выражения соотношения экономических явлений в пространстве ( по городам, регионам, странам и т.д.) используют территориальные индексы. При построении территориальных индексов особое значение приобретает вопрос о весах индекса. Например, при сравнении уровня себестоимости по двум регионам можно с равным правом выбрать в качестве веса количество произведенной продукции каждого региона. Различия индексов, рассчитанных с весами разных регионов, могут быть существенными. Поэтому к построению территориальных индексов необходим особый подход по сравнению с индексами, выражающими изменение явления во времени.

Территориальный индекс может быть получен сопоставлением уровня исследуемого явления по городу со средним уровнем этого явления для всей страны, региона и т.д. Другой способ построения территориальных индексов основан на непосредственном сопоставлении уровней явления с применением стандартизованных (одинаковых) весов, общих для всех регионов. В этом случае территориальный индекс себестоимости будет равен:

I_z = ,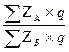

При построении территориальных индексов для количественных показателей способ стандартизованных весов удобнее использовать в виде среднего арифметического индекса, в котором рассчитанные предварительно территориальные индексы для каждой отрасли экономики, взвешиваются затем по структуре отраслей страны или региона. Расчет можно произвести по формуле:

В зависимости от методологии расчета различают: агрегатные индексы и средние индексы; цепные и базисные индексы.

Агрегатный индекс является формой сводного индекса, используемой для характеристики изменения сложного экономического явления. Числитель и знаменатель агрегатного индекса представляют собой суммы произведений индексируемых величин двух сравниваемых периодов (или фактических и плановых значений и т.д.) на некоторые одинаковые для обоих периодов величины, называемые весами агрегатных индексов. Агрегатный индекс является основной формой индекса, так как в этом индексе отчетливо выступает отношение двух абсолютных величин, различающихся за счет изменения изучаемого явления. В агрегатном индексе изменяется только индексируемая величина, а вес остается неизменным, тем самым его влияние на величину индекса элиминируется.

J_p =

I_w = : ,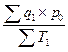

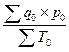
На величине индекса переменного состава отражается не только изменение уровня изучаемого явления, но также изменение удельных весов элементов с различным уровнем этого явления во всей совокупности, то есть изменение состава.

Например, индекс постоянного состава производительности труда рассчитывается по формуле:

I_w =

Средний арифметический индекс представляет собой среднюю арифметическую из индивидуальных индексов. Простая средняя арифметическая из индивидуальных индексов ( 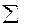i : n) на практике не применяется, так как в ней не отражается удельный вес каждого отдельного элемента во всей совокупности. Средний арифметический индекс рассчитывается только как взвешенная величина.

Формула арифметического индекса получается путем замены значения индексируемой величины в числителе агрегатного индекса на равное ему произведение индивидуального индекса на значение индексируемой величины другого периода. Например, заменив в числителе агрегатного индекса физического объёма продукции количество продукции текущего периода q₁ произведением i_q q₀ (где i_q=q₁:q₀), получим средний арифметический индекс физического объёма продукции.

I_q = .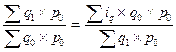

Средний гармонический индекс представляет собой среднюю гармоническую из индивидуальных индексов. На практике средний гармонический индекс рассчитывается только как взвешенная величина. Для получения формулы данного индекса индексируемая величина, находящаяся в знаменателе агрегатного индекса, заменяется через индивидуальный индекс и индексируемую величину другого периода. Например, для построения среднего гармонического индекса цен заменяют в агрегатном индексе цену базисного периода (р₀) равным ей отношением р₁: i _p.

I_p = .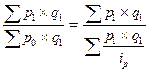

Этот индекс является средней гармонической из индивидуальных индексов цен (i_p), взвешенной по величине товарооборота текущего периода (p₁ q₁).

Средние индексы рассчитываются в тех случаях, когда нет необходимой информации для расчета агрегатного индекса.

Индексы предназначены для решения следующих основных задач: характеристика изменения сложного социально-экономического явления во времени, пространстве или по сравнению с запланированными показателями; измерение значений отдельных факторов, их влияния на общее изменение изучаемого явления в динамике.

Источник

Статистика

Понятие об индексах.

В практике статистики индексы наряду со средними величинами являются наиболее распространенными статистическими показателями. С их помощью характеризуется развитие национальной экономики в целом и ее отдельных отраслей, анализируются результаты производственно-хозяйственной деятельности предприятий и организаций, исследуется роль отдельных факторов в формировании важнейших экономических показателей, выявляются резервы производства. Индексы используются также в международных сопоставлениях экономических показателей, определении уровня жизни, мониторинга деловой активности в экономике и т.д.

Статистический индекс – это относительная величина сравнения сложных совокупностей и их отдельных единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не могут быть просуммированы.

Например, ассортимент продовольственных товаров состоит из продуктов, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, яйцо – в штуках, консервы – в условных банках и т.п. Для определения общего объема производства и реализации продовольственных товаров суммировать данные учета разнородных товарных масс в натуральных измерителях нельзя. То же относится и к непродовольственным товарам, к продукции крупных промышленных предприятий и т.д.

Для получения в сложных статистических совокупностях обобщающих, суммарных величин прибегают к индексному методу. Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям. Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство.

В зависимости от степени охвата подвергнутых обобщению единиц изучаемой совокупности индексы подразделяются на индивидуальные и общие.

Индивидуальные индексы характеризуют изменения отдельных единиц изучаемой совокупности. Например, при изучении оптовой реализации продовольственных товаров изменения в продаже отдельных товаров дают индивидуальные (однотоварные) индексы.

Общие или сводные или агрегатные индексы выражают обобщающие результаты совместного изменения всех единиц, образующих статистическую совокупность. Например, показатель изменения объема реализации товарной массы продуктов питания в отдельные периоды будет общим индексом физического объема товарооборота. Из общих индексов выделяют иногда групповые индексы (субиндексы), охватывающие только часть (группу) единиц в изучаемой статистической совокупности.

Важной особенностью общих индексов является то, что они обладают синтетическими и аналитическими свойствами.

Синтетические свойства индексов состоят в том, что посредством индексного метода производится соединение (агрегирование) в целое разнородных единиц статистической совокупности.

Аналитические свойства индексов состоят в том, что посредством индексного метода определяется влияние факторов на изменение изучаемого показателя. На основе изучения состава и роли факторов, выявления силы их действия осуществляются возможности квалифицированного управления развитием экономических процессов не только в нужном направлении, но и с заранее заданными параметрами.

Для определения индекса надо произвести сопоставление не менее двух величин. При изучении динамики социально-экономических явлений сравниваемая величина (числитель индексного отношения) принимается за текущий (или отчетный) период, а величина, с которой производится сравнение, – за базисный период. Если в индексном отношении сравнивается величина фактического уровня развития с величиной планового задания, то основание сравнения называют плановым уровнем. Кроме того, при сравнении текущих величин с предшествующими получают цепные индексы (при сравнении с базисными величинами – базисные индексы).

Индивидуальные индексы обозначают i, а общие – I.

Индивидуальные индексы физического объема реализации товаров определяют по формуле

где q₁ и q₀ – количество продажи отдельной товарной разновидности в текущем и базисном периодах в натуральных измерителях.

Индивидуальные индексы цен определяются по формуле

где p₁ и p₀ – цены за единицу товара в текущем и базисном периодах.

Результаты расчета индексных отношений могут выражаться в коэффициентах или в процентах.

Источник