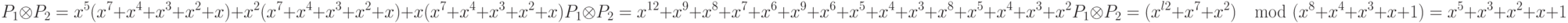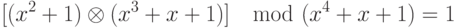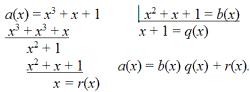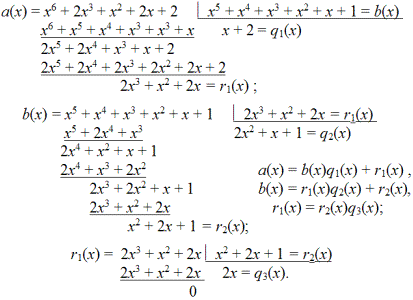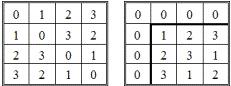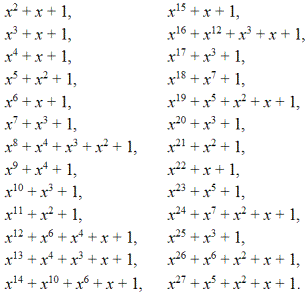обратный многочлен в поле
Конечные поля многочленов.
В дальнейшем будем обозначать Zp[x]\f(x) как GF(p k ) (поле Галуа).
Заметим, что GF(p α ) имеет характеристику p, и GF(p) (то есть Zp) является подполем GF(p α ) для соответствующего p.
Каждый ненулевой элемент поля обратим, и обратный элемент можно найти с помощью расширенного алгоритма Евклида.
Продемонстрируем процедуры сложения, умножения многочленов и отыскание обратного элемента в Z2[x]\f(x) на примере:
Отыщем обратный к (x+1) по модулю f(x):
Поскольку GF(p α ) является конечным полем, то, как известно из алгебры, мультипликативная группа его ненулевых элементов является циклической, а значит в нем существует порождающий элемент. Если многочлен f(x) степени m неприводим, и порождающим элементом мультипликативной группы ненулевых элементов поля Zp[x]\f(x) является многочлен g(x)=x, то f(x) называют примитивным многочленом.
Например, нетрудно проверить, что многочлены x 3 +x 2 +1 и x 3 +x+1 являются примитивными над Z2.
Теорема 1
Неприводимый многочлен f(x) из Zp[x] степени m примитивен 
Теорема 2
Для любого m≥1 существует φ(p m —1)/m примитивных многочленов степени m над полем Zp.
Заметим, что не существует эффективного детерминированного алгоритма нахождения примитивных многочленов. Проще всего генерировать многочлен заданной степени случайным образом и проверять, не является ли он примитивным, например, с помощью критерия Эйзенштейна.
Для конечных полей многочленов, так же как и для Zp, определено понятие дискретного логарифма.
Конечное поле GF(256) и немного магии
Введение
Будучи студентом я посещаю занятия по криптографии. И разумеется этот курс не мог обойти вниманием стандарт AES.
При реализации данного алгоритма встает вопрос о реализации полей GF(2^8), что будет освещено в данной статье. Будут рассмотрены: битовая магия для умножения элементов поля, шаблоны для генерации таблиц замен на этапе компиляции.
Вторая часть предполагает, что читатель имеет доступ к компилятору с поддержкой C++14. Первая часть будет написана в стиле Си.
Сперва рассмотрим как образуется поле с простым числом элементов GF(p).
Его элементы — числа . Операции сложения и умножения — сложение и умножение по модулю p.
2 + 6 = 8%7 = 1
4 * 3 = 12%7 = 5
На основе полей GF(p) строятся более общие поля GF(p^q), p — простое, q — натуральное.
Элементы таких полей — многочлены над полем GF(p):
Сложение в данном поле будет непосредственно сложением данных многочленов.
Например при p=2, q=3:
С умножением чуть сложнее. Для того что бы определить его требуется многочлен Q(x) степени q, неприводимый над GF(p) (не существует двух многочленов меньшей степени, в произведении дающих данный). К счастью для любых p и q такой многочлен существует.
Когда многочлен Q(x) выбран, для того что бы найти произведение двух элементов a*b поля нужно:
Q(x) = x^3 + x + 1 (Неприводимый многочлен)
a = x^2 + 1, b = x^2
a(x) * b(x) = x^4 + x^2
(x^4 + x^2) % Q(x) = (x^4 + x^2 — x*Q(x)) % Q(x) = (x^3 + x) % Q(x) = (x^3 + x — Q(x)) % Q(x) = 1 = a * b
Q(x) = x^2 + x + 2 (Неприводимый многочлен)
a = x+2
b = 2x + 2
a(x) * b(x) = 2x^2 + (6%3) * x + (4%3) = 2x^2 + 1
(2x^2 + 1) % Q(x) = (2x^2 + 1 — 2Q(x)) % Q(x) = ((-2%3)x + (-3%3)) % Q(x) = x % Q(x) = x
Реализация
Итак, требуется реализовать следующие операции в поле GF(256) над многочленом x^8 + x^4 + x^3 + x + 1:
Первое что приходит на ум — реализовать произведение многочленов наивным алгоритмом:
После чего написать функцию нахождения остатка от деления на многочлен.
В этот момент я задумался что будет дальше. А дальше меня ждал расширенный алгоритм Евклида для многочленов, и хоть на самом деле это не так страшно, было решено подумать. А нельзя ли сделать это как-нибудь красиво? Жаль нельзя используя одну операцию перемножить два таких многочлена, найти остаток от деления на другой.
А точно ли нельзя? Посмотрим что нам мешает реализовать произведение многочленов через простое произведение.
По формуле для произведения многочленов имеем:
Для произведения двух чисел в двоичной системе счисление получаем почти аналогиное выражение:
Разница состоит в том, что для многочленов выражение определяет коэффициент при
.
Аналогичное высказывание для чисел не будет верно из-за того, что в предыдущем разряде могло произойти переполнение, меняющее значение рассматриваемого.
Как избавиться от переполнения? Очень просто. Рассмотрим следующую запись:
Поскольку при перемножении многочленов степени не выше 7 нельзя получить многочлен степени выше 14, разряду будет соответствовать сумма не более чем из 15 нулей и единиц (на самом деле легко убедиться что не более 8), а значит переполнение невозможно. Остается только преобразовать непосредственную сумму в сумму по модулю 2, выделив младший бит.
И так, если представлять полином как число, в котором каждому блоку соответствует блок из 4 бит, то произведение можно написать следующим образом:
Теперь разберем произведение как элементов поля Галуа.
Посмотрим на полином . В выбранном представлении он выглядит как q = 0x100011011. Невооруженным глазом видно большое количество нулевых блоков сразу после старшего блока. При умножении Q(x) на полином вида
мы получим полином:
или полином, старшие блоки которого есть . Этим мы и воспользуемся для написания функции умножения:
С умножением разобрались. Теперь нужно научиться находить обратный элемент по нему.
Вспоминаем, что поле без сложения и 0 образует группу из 255 элементов. Отсюда получаем, что для любого элемента x найдется число r, равное размеру подгруппы, образованной этим элементом, такое что x^r = 1. Так как порядок подгруппы — делитель порядка группы, , что с свою очередь дает нам что
. Тогда согласно определению обратного элемента имеем
:
Все? Ах, да, нужно уметь преобразовывать исходные байты в расширенную форму, в которой мы проводим все операции. Это можно сделать в лоб циклом, но не сегодня. Внутренний голос говорит что нужно использовать грязный трюк. В конце концов не я ли читал статью Обстоятельно о подсчёте единичных битов?
Обозначим байт как 0bABCDEFGH. Первое что приходит в голову это умножение на 0b1001001 трех младших бит:
0bFGH * 0b1001001 = 0bFGHFGHFGH
0bFGHFGHFGH | 0b100010001 = 0bF000G000H, или три младших бита встали на свои места.
Аналогично проделывается над средней тройкой бит и старшей парой. Трюк был придуман. Но три умножения это как то слишком много. Нельзя ли делать тоже самое в раз по 4 бита? Рассмотрев многочисленные выборки бит я сумел найти лишь одну четверку с которой это работает:
Обратите внимание на младшие биты 7, 6, 1, 0 блоков. Для них характерны наличие нужного бита на своем месте и что не менее важно, невозможность переполнения за счет младших (относительно данных) бит.
Как было сказано, двух парных четверок бит я не нашел. Неудача? Не совсем. Если мы способны поставить семь из восьми бит на свои места использовав 2 умножения, мы можем поставить все 8, водрузив последний на свое место простым сдвигом.
С сжатием обратно дела обстоят проще. Следующее умножение показывает как сжать 4 бита:
С учетом этого код приобретает следующий вид:
Пусть считает компилятор
Зачем использовать довольно дорогие преобразования байт когда можно воспользоваться просчитанной заранее таблицей? В данной секции я поясню как просчитать её на этапе компиляции при помощи магии шаблонов на примере таблицы обратных элементов по сложению.
Первым делом всем ранее написанным функциям добавим спецификатор constexpr (с этого момента компиляция потребует поддержки с++14). Это позволит использовать данные функции в качестве аргументов шаблонов.
Рассмотрим что происходит при попытке использовать GaloisTable ::data.
Компилятор находит соответствующую специализацию шаблона, в которой data определена как GaloisTable ::data. Она в свою очередь определена через GaloisTable ::data и так далее.
Когда m достигает 0 компилятору удается найти более конкретную специализацию шаблона (А компилятор всегда предпочитает более конкретную). Тут то и завершается рекурсивное задание классов и из последовательности в Data… создается сам массив, заимствованный всеми предыдущими классами.
Data… на это шаге будет ничем иным как inverse(0), inverse(1), …, inverse(255), что нам и было нужно.
Надеюсь, статья была чем-либо полезной.
Update: Префикс Galua заменен на Galois.
Обратный многочлен в поле
Сложение и операции вычитания на полиномах — та же самая операция.
Умножение
Умножение в полиномах — сумма умножения каждого элемента одного полинома с каждым элементом второго полинома. Однако необходимо отметить три особенности.
Сначала покажем, как умножить два полинома согласно вышеупомянутому определению. Позже будет дан более эффективный алгоритм, который может использоваться компьютерной программой.
Чтобы найти конечный результат, разделим полином степени 12 на полином степени 8 (модуль) и сохраним только остаток. Процесс деления тот же самый, что и в обычной алгебре, но мы должны помнить, что здесь вычитание то же самое, что и сложение. Рисунок 6.3 показывает процесс деления.
Мы используем расширенный евклидов алгоритм, как это показано в таблице 6.2:
| q | rj | r2 | r | tj | t2 | t |
|---|---|---|---|---|---|---|
| x 2 +1 | (x 4 +x+1) | (x 2 +1) | (x) | (0) | (1) | (x 2 +1) |
| (x) | (x 2 +1) | (x) | (1) | (1) | (x 2 +1) | (x 3 +x+1) |
| (x) | (x) | (1) | (0) | (x 2 +1) | (x 3 +x+1) | (0) |
| (1) | (0) | (x 3 +x+1) | (0) |
Будем использовать расширенный евклидов алгоритм, как это показано в Таблице 6.3:
| q | rj | r2 | r | tj | t2 | t |
|---|---|---|---|---|---|---|
| (x 3 ) | (x 8 +x 4 +x 3 +x+1) | (x 5 ) | (x 4 +x 3 +x 2 +x+1) | (0) | (1) | (x 3 ) |
| (x+1) | (x 5 ) | (x 4 +x 3 +x+1) | (x 3 +x 2 +1) | (1) | (x 3 ) | (x 4 +x 3 +1) |
| (x) | (x 4 +x 3 +x+1) | (x 3 +x 2 +1) | (1) | (x 3 ) | (x 4 +x 3 +1) | (x 5 +x 4 +x 2 +x) |
| (x 3 +x 2 +1) | (1) | (0) | (x 4 +x 3 +1) | (x 5 +x 4 +x 2 +x) | (0) | |
| (1) | (0) | (x 5 +x 4 +x 2 +x) | (0) |
Результат может быть легко проверен умножением этих двух полиномов и определением остатка деления по модулю.
Умножение, использующее компьютер
| Степень | Операция | Новый результат | Вычитание |
|---|---|---|---|
x 0  P2 P2 | x 7 +x 4 +x 3 +x 2 +x | НЕТ | |
x 1  P2 P2 | x  (x 7 +x 4 +x 3 +x 2 +x) (x 7 +x 4 +x 3 +x 2 +x) | x 5 +x 2 +x+1 | ДА |
x 2  P2 P2 | x  (x 5 +x 2 +x+1) (x 5 +x 2 +x+1) | x 6 +x 3 +x 2 +x | НЕТ |
x 3  P2 P2 | x  (x 6 +x 3 +x 2 +x) (x 6 +x 3 +x 2 +x) | x 7 +x 4 +x 3 +x 2 | НЕТ |
x 4  P2 P2 | x  (x 7 +x 4 +x 3 +x 2 ) (x 7 +x 4 +x 3 +x 2 ) | x 5 +x+1 | ДА |
x 5  P2 P2 | x  (x 5 +x+1) (x 5 +x+1) | x 6 +x 2 +x | НЕТ |
| P1 x P2 = (x 6 +x 2 +x)+(x 6 +x 3 +x 2 +x)+(x 5 +x 2 +x+1) = x 5 +x 3 +x 2 +x+1 | |||
| Степень | Операция сдвига влево | ИСКЛЮЧАЮЩЕЕ ИЛИ |
|---|---|---|
x 0  P2 P2 | 10011110 | |
x 1  P2 P2 | 00111100 | (00111100)  (00011010) = 00100111 (00011010) = 00100111 |
x 2  P2 P2 | 01001110 | 01001110 |
x 3  P2 P2 | 10011100 | 10011100 |
x 4  P2 P2 | 00111000 | (00111000)  (00011010) = 00100011 (00011010) = 00100011 |
x 5  P2 P2 | 01000110 | 01000110 |
P1  P2 = (000100110) P2 = (000100110)  (01001110) (01001110)  (01000110) = 00101111 (01000110) = 00101111 | ||
Таблица 6.7 показывает умножение. Затемненные клетки (единичные) дают обратные пары при умножении.
Обратный многочлен в поле
Теперь мы приобрели необходимые сведения для действия и с многочленами n-ой степени вида:
Если an(c) = 0, то c — корень многочлена an(x). Число c будет корнем an(x) тогда и только тогда, когда an(x) делится на скобку (x – c) без остатка. Действительно, пусть
Поиск корней многочлена an(x) равносилен поиску его линейных делителей; при a0 = 1 получим
Общее число корней многочлена an(x) всегда равно n. Однако могут встречаться кратные корни, тогда
Это называется каноническим разложением многочлена an(x) на простые (неприводимые) множители. Многочлен a(x) называется приводимым, если он может быть разложен в произведение двух множителей без остатка —
Но известна ситуация, когда многочлен a(x) часть корней имеет в поле действительных чисел, а часть — в поле комплексных чисел. Таким образом, о приводимости или неприводимости многочленов можно говорить лишь по отношению к данному полю, поскольку многочлен, неприводимый в одном поле, может оказаться приводимым в другом. Ранее приведенный пример с многочленом x³ – 1 в этом отношении показателен.
Далее нас будут интересовать многочлены a(x), у которых коэффициенты ai взяты из числового поля GF(p). Эти многочлены образуют кольцо относительно сложения и умножения. Пусть этими многочленами будут
а числовое поле GF(2) = <0, 1>, тогда сумма и произведение a(x) и b(x) дадут два новых многочлена —
В своей совокупности многочлены образуют именно ассоциативно-коммутативное кольцо, но не поле, поскольку не существует таких многочленов степени больше единицы, которые бы при перемножении давали единицу: a(x) · b(x) = 1, т.е. в алгебре многочленов для каждого ее элемента отсутствует обратный.
Многочлены можно делить друг на друга:
Многочлен b(x) называется делителем a(x), если остаток r(x) равен нулю. Наибольший общий делитель двух многочленов a(x) и b(x) находится по алгоритму Евклида, только роль чисел уже выполняют многочлены. Покажем, как его найти на многочленах a (x) и b(x) с коэффициентами, взятыми из числового поля GF(3):
Следуем алгоритму Евклида:
Таким образом, НОД(a(x), b(x)) = x² + 2x + 1 = r2(x). Чтобы найти НОК, необходимо знать результат от перемножения исходных многочленов; он равен:
Для многочлена, как и для чисел, можно ввести сравнение многочлена a(x) по модулю многочлена q(x): a(x) = r(x) mod q(x). А раз так, то можно говорить и о поле многочленов GF(q) над числовым полем GF(p). Если GF(2), а q(x) = x³ + 1, то имеем поле многочленов GF(x³ + 1), состоящее из восьми многочленов:
Здесь p = 2 называется характеристикой поля GF(p); характеристика определяет размерность или порядок полей многочлена: q = p n = 2³ = 8, где n — степень многочлена q(x). Перемножим два произвольных элемента поля GF(q) по mod q(x):
Продолжая далее перемножать элементы GF(q), мы могли бы составить таблицу умножения. Но мы составим таблицы сложения (табл. 2.74) и умножения (табл. 2.75) для другого поля многочленов — GF(x² + x + 1), размерность которого в два раза меньше: <0, 1, x, x + 1>. Каждому элементу последнего множества можно поставить в соответствие либо двоичное число: <00, 01, 10, 11>, либо десятичное: <0, 1, 2, 3>, тогда таблицы сложения (табл. 2.74) и умножения (табл. 2.75) поля GF(x² + x + 1) предстанут в виде числовых таблиц (табл. 2.76) и (табл. 2.77), схожих с табл. 2.70 и табл. 2.71.
Таблица 2.74 Таблица 2.75
Таблица 2.76 Таблица 2.77
Циклическая группа по умножению (табл. 2.75) изоморфна циклической группе корней кубических из единицы (табл. 2.69), только в качестве элементов в данном случае выступают многочлены: c1 = 1, c2 = x, c3 = x + 1, получающиеся за счет расширения числового поля, подобное расширению числового поля действительных чисел за счет комплексных. Если в качестве образующего взять элемент c2 = x, то последовательным возведением его в первую, второю и третью степень получим все три элемента: x 1 = x, x² = x + 1, x³ = 1. Эти элементы являются корнями уравнения
решенного в поле GF(2).
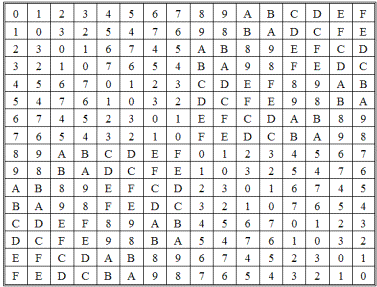
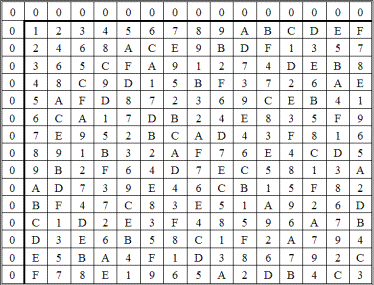
Приведем примеры таблиц сложения и умножения для следующих полей многочленов:
с порождающим многочленом g(x) = x² + x + 2; таблица сложения — табл. 2.78, таблица умножения — табл. 2.79.
с порождающим многочленом g(x) = x 4 + x³ + 1; таблица сложения — табл. 2.80, таблица умножения — табл. 2.81.
Все выписанные таблицы определяют знакомые нам коммутативные группы. Если по таблицам составить регулярные подстановки, то их структура сразу же будет узнаваема. Естественно, для этих групп можно найти все их подгруппы, включая нормальные делители. Та роль, которая в группах принадлежит нормальным делителям, в кольцах принадлежит идеалам. Подмножество I кольца K называется идеалом, если оно является подгруппой аддитивной группы кольца. Для того чтобы подмножество I было идеалом в K, необходимо выполнение единственного условия, а именно: если i ∈ I и k ∈ K, то их произведения ik и ki должны принадлежать подмножеству I. Если в определении идеала отказаться от требования, что оба произведения ik и ki принадлежат I, то придем к понятию одностороннего идеала: если ik ∈ I — правый идеал, если ki ∈ I — левый идеал. Всякий идеал кольца будет подкольцом. Пересечение любой системы идеалов кольца будет идеалом.
В кольцах Ли и Ёрдана левые и правые идеалы совпадают; такие идеалы называются двухсторонними. Из определения идеала следует, что во всяком кольце K идеалами являются само кольцо K и так называемый нуль-идеал, состоящий из одного нулевого элемента. Кольцо, не содержащее других идеалов, кроме этих двух, называется простым. Все тела и поля являются простыми кольцами.
Можно было бы продолжать вводить для колец и полей понятия гомоморфизма, фактормножества и т.д., только все это нас слишком уведет в сторону. Между тем, овладев техникой анализа групп, провести подобный анализ для полей не составит большого труда. Поэтому вернемся непосредственно к многочленам.