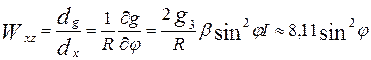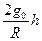нормальное поле силы тяжести

Нормальное поле силы тяжести.

Как же определяется нормальное поле? С этого мы начинали рассмотрение физико-геологических основ гравиразведки, остановившись на том, что существуют специальные формулы для вычисления g₀. Эти формулы используют применительно к какой-то конкретной модели Земли, то есть к сфероиду или эллипсоиду относимости с вполне определенными геометрическими характеристиками (относительным сжатием α).

В России за эту конкретную модель принят эллипсоид Красовского (α=1/298,2), а остальной мир использует модель Хейфорда (α=1/297,8). Параметры эллипсоида (сфероида) определяют из совместной обработки данных астрономо-геодезических и гравиметрических работ, а также спутниковых наблюдений. Формулы для вычисления g₀ получают дифференцированием потенциала W по r (радиусу Земли) или по n (нормали к поверхности Земли; нормаль практически совпадает с радиусом, поскольку форма Земли близка к сферической), направив их по оси Z с последующим переходом от прямоугольной системы координат к сферической.

Впервые такую формулу получил французский математик Клеро для сферической модели Земли (для шара), то есть без учета ее относительного сжатия α.

Формула Клеро g₀ = g_э (1 + βsin 2 φ) позволяет рассчитать g₀ для любой широты (напомним, что географической широтой называется угол, образуемый радиусом R, на котором находится рассматриваемая точка Р, где определяется g_0, с плоскостью экватора. И это при том, что начало координат помещено в центр Земли, оси X и Y расположены в плоскости экватора, а ось Z совмещена с осью вращения Земли, как показано на рис.5

В приведенной формуле Клеро g_э – значение силы тяжести, измеренное на экваторе, а

β = 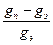, то есть разность значений силы тяжести, найденных на полюсе g_п и на экваторе g_э, отнесенная к g_э.

Позднее, когда стало очевидным, что сферическая модель слишком груба для описания фигуры Земли, в формулах нормального значения появилось еще одно слагаемое, отражающее сфероидальность нашей планеты. Тем самым эти формулы приобрели такую структуру:

g₀ = g_э (1 + βsin 2 φ – β₁sin 2 2 φ), где β₁ = 1/8α 2 + ¼ α β (где α – относительное сжатие сфероида, а значения коэффициентов g_э и β определяются экспериментально.

Среди множества формул этой структуры наиболее известны формулы Гельмерта и Кассиниса. Формула Гельмерта с числовыми значениями g_э = 978.030; β = 0,005302 и β₁ = 0,000007 получены с использованием параметров эллипсоида Красовского и со значением g_э, полученным в результате осреднения 108 измерений этой величины на экваторе в 1908 году. Эти измерения выполнил Гельмерт с использованием самых лучших на то время приборов.

Формула Гельмерта используется для вычисления нормальных значений силы тяжести на территории России.

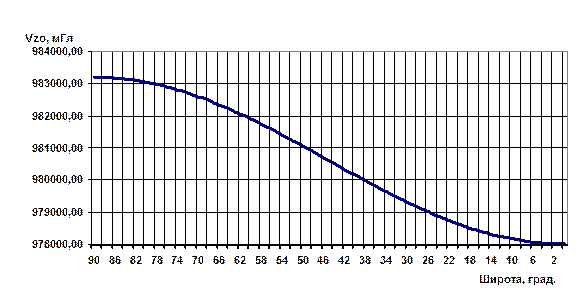
Формула Кассиниса (1930г) на конгрессе геофизиков признана как международная. В качестве модели Земли, то есть для определения α здесь использован эллипсоид Хейфорда. В вычисленных по этим и других формулам, где использованы иные величины коэффициентов g_э, β, β₁ и другие оценки α, нормальные значения оказываются различными: расхождения в зависимости от широты составляют 6 – 19 мГал.

Может возникнуть вопрос, почему в России используются формулы и модели Земли, отличные от принятых международным сообществом. Это обусловлено двумя достаточно серьезными причинами. Во-первых, эллипсоид Красовского лучше описывает фигуру Земли в пределах территории России. Во-вторых, переход на формулу Кассиниса потребовал бы создания новых топографических карт для всей гигантской территории нашей страны, поскольку все эти карты составлены на основе эллипсоида Красовского. Такая работа потребовала бы громадных финансовых средств, а результат оказался бы хуже, чем с использованием старых карт.

Нормальные значения на поверхности однородного земного сфероида вычисляются и для градиентов силы тяжести.

Изменение нормального значения силы тяжести по долготе пренебрежимо мало. Поэтому можно записать, что W_yz=0. Нормальное значение горизонтального градиента W_xz, принимая во внимание, что элемент дуги меридиана в линейной мере составит dx=Rdφ (R— радиус Земли, dφ – приращение широты, см.рис.5) можно записать в виде

Нормальное значение вертикального градиента W_zz = 0,3086 Е

Аномалии силы тяжести.

Под аномалией силой тяжести, как уже неоднократно упоминалось, понимается разность g_набл –g₀. Однако, измеряют (наблюдают) силу тяжести на физической поверхности Земли, тогда как нормальные значения определяются для поверхности сфероида, которая близка к уровню моря. Поэтому наблюденные и нормальные значения необходимо привести к единому уровню. Это приведение или редуцирование силы тяжести осуществляется введением ряда поправок.

Первая из них – поправка за высоту точки наблюдения над уровнем моря или редукция Фая. При введении этой поправки притяжение масс, расположенных между физической поверхностью Земли и уровнем моря не учитывается, из-за чего эта поправка называется также поправкой за свободный воздух. Ее определяют как разность значений силы тяжести на двух поверхностях Земли: с радиусом R и R+h, где h – высота над уровнем моря (рис.6).

В точке Р с высотой h определяется значение g, а для ее проекции на уровень моря Р’ вычисляется нормальное значение. В первом приближении нормальное значение силы тяжести

Вторая масса в законе Ньютона, из которого следует приближенное выражение для g_0, т.е как бы масса измерительного элемента прибора – гравиметра принимается равной единице. Значит, поправка за высоту может быть определена так:

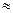
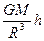
δ g_{h =} GM [1/ R 2 _ 1/(R+h) 2 ] 2 =

Та же величина получается дифференцированием 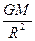по r.

— это нормальный вертикальный градиент силы тяжести, равный 3086 E

Такие аномалии для решения геологических задач использовать нецелесообразно, поскольку они коррелированны с рельефом. Это означает, что для одинакового разреза в высокогорье и на равнине значения δg Ф получатся разными, так как на высокогорье отмечаются более высокие отметки рельефа. Таким образом, становится очевидным, что эти аномалии лишены геологического смысла. Они используются в науке, изучающей фигуру Земли и называемой геодезическая гравиметрия.

Чтобы аномалии стали содержательными в геологическом отношении, необходимо ввести поправку за притяжение масс, расположенных между физической поверхностью и уровнем моря. Эту поправку называют поправкой за промежуточный слой. Она вводится в предположении, что притяжение таких масс эквивалентно притяжению горизонтальной пластины (слоя) бесконечного простирания с толщиной, равной h.

Такая поправка определяется по формуле

где σ – плотность пород промежуточного слоя. Величина σ для разведуемой площади определяется экспериментально. При производстве региональных съемок она берется равной 2,3·10 3 кг/м 3 для равнинных территорий и 2,67·10 3 кг/м 3 для горно-складчатых регионов.

Притяжение промежуточных масс увеличивает значение силы тяжести в точке наблюдения и поэтому знак этой поправки противоположен знаку поправки за высоту. Суммарная поправка за высоту и промежуточный слой называется поправкой Буге:

Аномалия, вычисленная с введением редукции Буге, называется аномалией Буге

Именно аномалии Буге являются геологически содержательными и потому используются в геологии.

Еще одна поправка – за негоризонтальность рельефа – вводится при выполнении работ на территориях со сложным, расчлененным рельефом. Необходимость ее введения обусловлена тем, что неровности рельефа (напомним, что в предыдущих редукциях эти неровности никак не учитывались) всегда уменьшают измеряемое значение силы тяжести, поскольку суммарный вектор их притяжения (отталкивания) направлен в сторону, противоположную вектору притяжения неоднородностей недр и Земли в целом. Это хорошо видно из рассмотрения рисунка 7.

Рис. 7. К введению поправки за не горизонтальность рельефа.

Итак, для решения геологических задач в России используют результаты гравиметрических съемок, представленные в виде карт аномалий Буге, иногда с введением поправки за не горизонтальность рельефа. Зарубежные геофизики пользуются для тех же целей картами изостатических аномалий. О теории изостазии и изостатической поправке можно прочитать в учебном пособии [1].

Источник

Нормальное поле силы тяжести

В гравиразведке нас интересуют прежде всего аномальные значения силы тяжести, но для их получения необходимо знать нормальные значения поля на поверхности Земли.

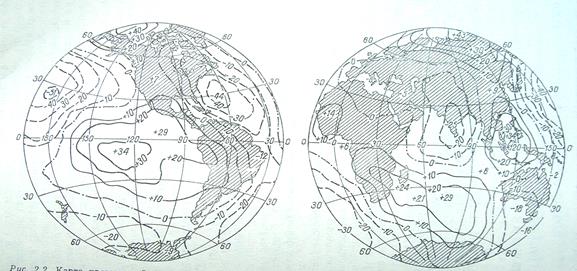
В гравиразведке в качестве нормального поля используют некоторую уровенную (эквипотенциальную) поверхность, в каждой точке которой сила тяжести направлена по нормали. Эта поверхность совпадает с невозмущенной ветром и течениями поверхностью океана и продолжается под поверхностью континентов так, что в любой его точке сила тяжести направлена по нормали. Такая поверхность называется геоидом и принимается за фигуру Земли. Совпадая на океанах с физической поверхностью Земли, геоид представляет собой следующее после эллипсоида приближение к истинной фигуре Земли именно на океанах. На континентах переход от эллипсоида к геоиду не решает задачи следующего приближения, т. к. геоид является фигурой неправильной и, в отличие от эллипсоида, не может быть выражен аналитически, что исключает его использование при решении геодезических задач. При выводе формул нормального распределения силы тяжести некоторые авторы одновременно вычислили и построили карты отклонений геоида от сфероида (рис. 2.7).

Рис. 2.7. Карта превышений геоида В. Каула ( в метрах) над сфероидом со сжатием 1/284,26 (по Миронову,1980)

Для сфероида в 1743 году французский ученый А. Клеро получил формулу нормального поля силы тяжести с точностью до малых второго порядка:

Точная формула распределения силы тяжести на сфероиде была предложена итальянским геодезистом К. Сомильяна:

Если в правой части этого равенства сделать подстановку β = (g_p – g_e)/g_e и α = (a-b)/a и разложить в ряд до малых третьего порядка, получим уточненную формулу Клеро :

γ_о = g_e(1+β sin 2 φ + β₁ sin 2 2φ). (2.28)

1. Формула Гельмерта выведена по результатам более 1600 измерений силы тяжести, распределенных по 9 широтным зонам, каждая из которых была разделена на 10-градусные трапеции. Она имеет вид

Рис. 2.8. График значений нормального поля, рассчитанных по формуле Гельмерта.

Для привязки к новой Потсдамской системе здесь введена поправка – 14 мГл. График нормальных значений, полученных по формуле Гельмерта, приведен на рис. 2.8. Для Томска, где широта φ = 56 о 26 I нормальное значение γ_о = 981610,46 мГл. Несмотря на то, что эту формулу считают устаревшей, она до сих пор применяется в России и странах бывшего СССР и СЭВ. Это связано с тем, что соответствующий ей эллипсоид имеет сжатие, близкое к эллипсоиду Красовского. Кроме того, по современным данным, полученным в результате изучения вариаций элементов орбит искусственных спутников, сжатие Земли α также весьма близко к эллипсоиду Красовского и составляет 1/298,25. Переход на новую формулу потребовал бы большой вычислительной работы.

2. В 1930 году на Международном геодезическом конгрессе в Стокгольме в качестве международной была принята формула Кассиниса для сфероида со сжатием α = 1/297:

γ_о = 978049 (1 + 0,0052884 sin 2 φ – 0.0000059 sin 2 2φ). (2.30)

Эта формула применяется в большинстве стран Европы и Америки.

В 1971 году на ассамблее Международного союза геофизики и геодезии в Москве была рекомендована новая формула нормального распределения силы тяжести, соответствующая так называемой референц-системе 1967 года:

γ_о = 978031,8 (1 + 0,005024 sin 2 φ – 0.0000059 sin 2 2φ). (2.31)

Для перехода от формулы Кассиниса к системе 1967 года надо вносить поправку, равную (-17,2 + 13,6 sin 2 φ) мгл.

Расхождение значений g_e и β по разным формулам объясняется недостаточной гравиметрической изученностью Земли. С накоплением данных будут появляться новые, все более точные формулы.

Источник

Геофизика

1.1. Основы теории гравиразведки

1.1.1. Нормальное гравитационное поле Земли

Согласно закону всемирного тяготения все тела притягиваются друг к другу с силой, пропорциональной их массе и обратно пропорциональной квадрату расстояния между ними. Для точечных масс, т. е. для масс, сосредоточенных в бесконечно малом объеме, справедлив закон всемирного тяготения Ньютона :

Если силу притяжения отнести к единичной массе ( т 1 = 1), то точечная масса ( т 2 = m ) будет притягивать ее с силой, равной ускорению силы притяжения :

В случае притяжения единичной массы телом, состоящим из отдельных точек ( n ) с массой ( m i ), уско­рение силы притяжения принимает вид

При непрерывном распределении притягиваемых масс сумма заменяется интегралом по всему занимаемому массами объему ( V ):

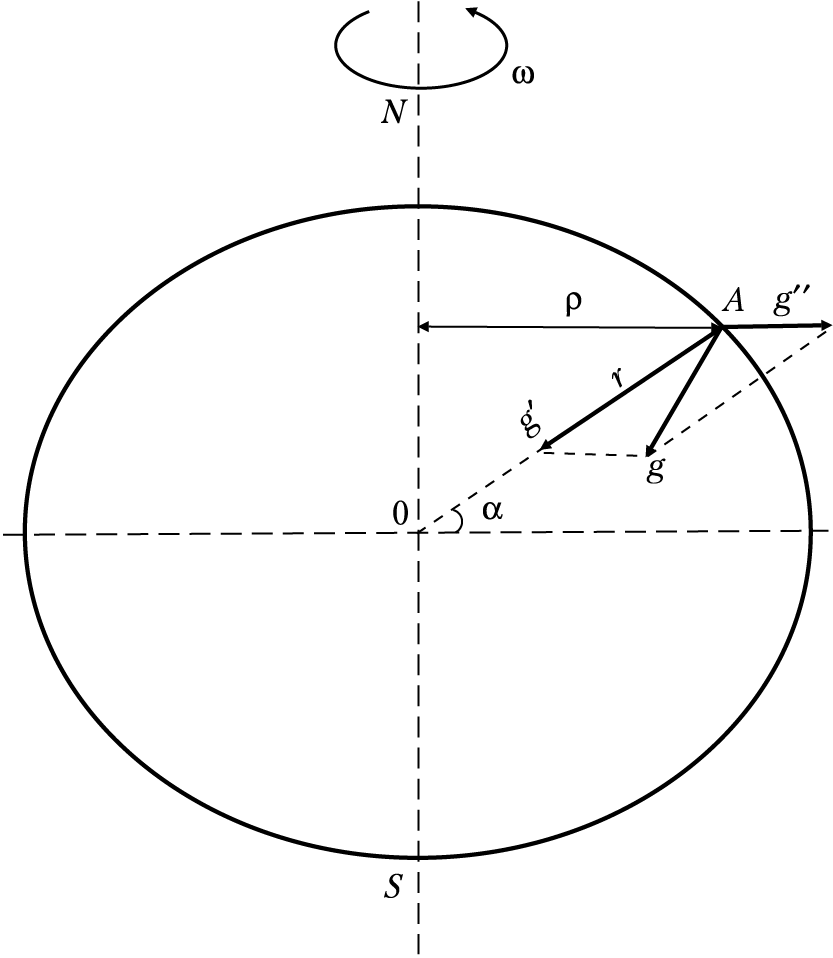
где М — масса Земли; r — средний радиус Земли, если притягиваемая точка А находится на ее поверхности (рис. 1.1).

Рис. 1.1. Нормальное поле силы тяжести и составляющие силы тяжести:

В общем случае нормальное гравитационное поле ( γ 0 ) Земли в виде шара представляет собой равнодействующую ускорений притяжения ( g ′ ) и центробежной силы ( g ′′ ):

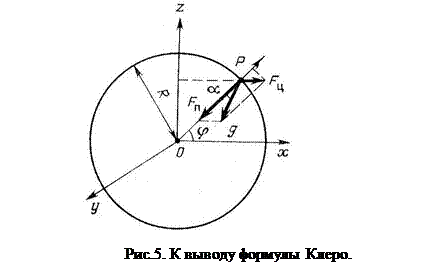
Если представить форму Земли в виде эллипсоида вращения малого сжатия ( α = 298,26), нормальное значение ускорения силы тяжести ( γ 0 ) можно выразить, например, по Элкинсу, формулой

γ 0 = g норм = g э (1 + 0,005302sin 2 φ – 0,000007sin 2 2 φ ), (1.9)

где g э — среднее значение поля на экваторе Земли; φ — широта наблюдения.

Это выражение позволяет рассчитать γ 0 на поверхности геоида, т. е. уровенной поверхности однородной Земли, совпадающей с невозмущенной поверхностью океана. С ростом количества точек наблюдений и повышением точности самих измерений g численные коэффициенты и их количество в формуле (1.9) будут меняться, поэтому существует несколько вариантов аналитического расчета значений нормального гравитационного поля как для всей поверхности Земли, так и для территорий отдельных государств, что необходимо учитывать при анализе гравитационных данных сопряженных или пограничных территорий.

1.1.2. Аномалии и редукции силы тяжести

Аномалией силы тяжести называют отклонение наблюденного значения ( g набл ) от нормального поля, теоретически рассчитанного для этой же точки, например, по формуле

где h — высота точки наблюдения над уровнем моря, выраженная в метрах.

Аномалией Фая ( Δ g Ф ) называют аномалию силы тяжести, полученную с учетом различия высот точек наблюдения:

Поправку за свободный воздух вводят в g набл со знаком плюс, если наблюдения проводят над уровнем моря, и со знаком минус, если наблюдения осуществляются ниже уровня моря. При погрешности относительных гравиметрических измерений ±0,01 мГал разница в высотах должна быть известна с погрешностью не более 4 см.

Аномалии Фая в основном используют в геодезической гравиметрии, а также при оценке геодинамического состояния земной коры и литосферы.

При наземных съемках на участках, приподнятых по отношению к уровню геоида, между поверхностью наблюдения и геоидом располагаются массы горных пород, которые при введении поправки за свободный воздух виртуально смещаются на величину h и «накладываются» на нижележащие массы, создавая как бы двойной плотностной эффект. Для исключения влияния масс, расположенных между поверхностью наблюдения и уровнем нормального поля, вводят поправку за промежуточный слой — поправку Буге ( Δ g Б ). Для выровненного спокойного рельефа поверхности наблюдения, когда массы промежуточного слоя можно представить в виде плоскопараллельного горизонтального слоя мощностью h (в м), эту поправку вычисляют по формуле (в мГал)

При расположении точки наблюдения выше уровня моря поправку Δ g Б вводят в наблюденные значения силы тяжести со знаком минус.

Поправка Буге, или полная поправка за промежуточный слой, имеет вид

В зависимости от точности наблюдений используют топографические карты различного масштаба, с помощью которых определяют влияние масс рельефа в области радиусом порядка 200 км и более от точки наблюдения. Причем для близко расположенных к точке наблюдения участков необходимы более точные карты рельефа местности.

Аномалия Буге ( Δ gБ ) представляет собой разность наблюденного и теоретического полей силы тяжести при введении соответствующих поправок:

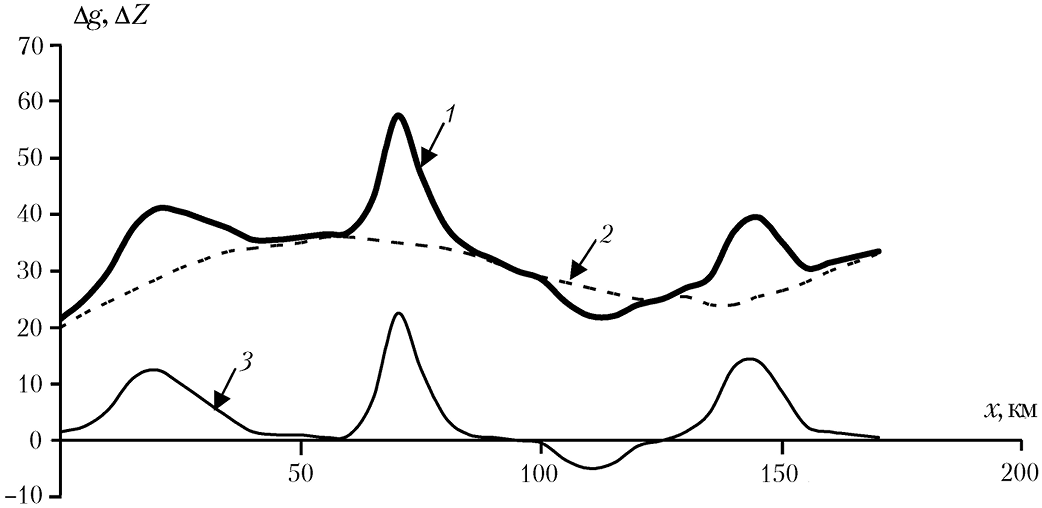
Аномалии Буге практически каждой территории представлены набором аномалий от разноглубинных и разномасштабных плотностных неоднородностей, отражающих локальные и региональные составляющие (рис. 1.2). Такое разделение аномалий связано с их разной частотной характеристикой: более высокочастотные аномалии относятся к локальным, а более низкочастотные — к региональным. Для выявления локальных аномалий Буге ( Δ g лок ) от, например, геологических структур осадочных бассейнов, отдельных интрузий, карстовых образований, рудных тел и других из наблюденного поля ( Δ g набл ) исключают региональную составляющую ( Δ g рег ), вычисляемую различными математическими (статистическими и др.) способами. На рисунке 1.2 приведен пример графического сглаживания наблюденного поля и выделения плавно изменяющегося регионального поля и локальной аномалии: Δ g лок = Δ g набл – Δ g рег (подробнее см. 1.4.2).

Рис. 1.2. Наблюденные (1), региональные (2) и локальные (3) аномалии силы тяжести

1.1.3. Плотность горных пород

Плотность горных пород и руд главным образом зависит от химико-минерального состава и пористости. Плотность изверженных и метаморфических пород определяется в основном минеральным составом и увеличивается при переходе от пород кислых к основным и ультраосновным в соответствии с увеличением железосодержащих минералов. Для осадочных пород плотность определяется прежде всего пористостью, водонасыщенностью и в меньшей степени минералогическим составом. Некоторые значения плотности приведены в табл. 1.1.

Таблица 1.1. Плотность некоторых веществ, пород, минералов и оболочек Земли

Источник

Нормальное поле и определение аномального потенциала (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3

НОРМАЛЬНОЕ ПОЛЕ И ОПРЕДЕЛЕНИЕ АНОМАЛЬНОГО ПОТЕНЦИАЛА

текст лекций по геодезической гравиметрии

для студентов специальности Прикладная геодезия

ГЛАВА 1. НОРМАЛЬНОЕ ГРАВИТАЦИОННОЕ ПОЛЕ

§1.1 ПОНЯТИЕ О НОРМАЛЬНОМ ПОЛЕ И СПОСОБАХ ЕГО ВЫБОРА

При изучении гравитационного поля Земли обычно используют фиктивное поле силы тяжести или притяжения, уровенные поверхности которых близки к уровенным поверхностям реального земного поля, но имеют более простую по сравнению с ними форму. Такое поле и описывающие его потенциал U силы тяжести или потенциал Vн притяжения называют нормальными. После введения нормального потенциала действительный потенциал W силы тяжести можно записать в виде

W=U+T, (1.1)

Т- аномальный или возмущающий потенциал.

Смысл введения нормального потенциала заключается в переходе от изучения потенциала W силы тяжести реальной Земли к изучению малой величины

Т = W – U. (1.2)

Таким образом, нормальный потенциал можно определить как потенциал достаточно простого вида, по возможности близкий к действительному

Существует несколько способов задания нормального потенциала. В одних используют понятие Нормальной Земли – модели Земли, обладающей теми или иными свойствами. Так, в геофизике задают поверхность и модель внутреннего строения нормальной Земли. Подобная модель впервые была введена А. Клеро(), который полагал, что Земля состоит из однородных жидких слоев и находится в состоянии гидростатического равновесия.

В топографии и инженерно-геодезических работах не очень высокой точности поле силы тяжести полагают однородным – все уровенные поверхности считают параллельными плоскостями, а силовые линии – параллельными прямыми. Это означает, что потенциал силы тяжести является линейной функцией

высоты h над исходной уровенной плоскостью U=Uо, а нормальная сила тяжести

(1.4)

постоянна по величине и направлению.

Еще один способ введения нормального поля основан на разложении потенциала притяжения в ряд шаровых функций, которое в сферических координатах r,F,L имеет вид

, (1.5)

r – радиус-вектор,F — геоцентрическая широта, L –долгота, Рпк(F) –присоединенная функция Лежандра первого рода степени n и порядка k. Нормальный потенциал получают, оставляя конечное число членов этого ряда. Так, оставляя только член нулевого порядка, т. е. полагая в (1.5) n=k =0, получают

. (1.7)

Это означает, что за нормальную Землю принят шар с центрально-симметричным распределением плотности. Произведение GM постоянной тяготения G на массу М Земли называют геоцентрической гравитационной постоянной.

Обычно в ряде (1.5) оставляют только четные зональные члены, не зависящие от долготы. Тогда нормальный потенциал притяжения получит вид

(1.8)

и будет симметричен относительно оси Z вращения Земли и плоскости экватора. Коэффициент А2по этого ряда при п=0 совпадает с (1.6) и является геоцентрической гравитационной постоянной, при п=1

Ат- средний экваториальный, С – полярный моменты инерции Земли соответственно.

Для получения нормального потенциала силы тяжести к (1.8) добавляют потенциал Q центробежной силы

(1.10)

. (1.12)

В геодезии обычно используют Нормальную Землю в виде идеальной планеты, имеющей форму эллипсоида вращения, причем эта поверхность является уровенной поверхностью ее потенциала силы тяжести, т. е. на поверхности эллипсоида выполняется условие

Особенно удобно объединение двух последних подходов к выбору нормального поля, когда потенциал уровенного эллипсоида представляют в виде ряда шаровых функций, а коэффициенты разложения (1.8) подбирают так, чтобы одна из уровенных поверхностей потенциала (1.12) силы тяжести была эллипсоидом вращения. Это позволяет построить непротиворечивую модель нормального поля, объединяющую геометрический и физический подходы к изучению Земли.

§1.2. ВНЕШНИЙ ПОТЕНЦИАЛ ПРИТЯЖЕНИЯ УРОВЕННОГО ЭЛЛИПСОИДА

Выберем Нормальную Землю в виде эллипсоида вращения

, (1.14)

на поверхности U=Uо, которого потенциал притяжения равен Vо, ao, bo – большая и малая полуоси соответственно. Зададим массу М этого эллипсоида и угловую скорость w его вращения. В теории потенциала доказано, что этих данных достаточно для определения внешнего гравитационного поля эллипсоида.

Центробежный потенциал Qо

Qо= , (1.15)

на поверхности эллипсоида изменяется в зависимости от расстояния Öхо2+уо2 до оси вращения, поэтому потенциал Vо притяжения на уровенном эллипсоиде не постоянен,

Vо =Uo-Qо= Uo— , (1.16)

хо, уо— координаты точки поверхности эллипсоида.

Потенциал эллипсоида удобно определять в специальной системе координат b, u, где b— малая полуось эллипсоида, софокусного эллипсоиду (1.14), u – приведенная широта (см. рис.1.1).В этой системе координат для потенциала притяжения уровенного эллипсоида получают замкнутое выражение

. (1.17)

u

Рис.1.1. Система координат сжатого эллипсоида

Здесь Е – линейный эксцентриситет, равный отрезку ОF на рис.1.1, F- фокус эллипсоидов, функция q определена выражением

q= (1.18)

, (1.19)

На поверхности эллипсоида при q= qо из (1.17) находим

(1.20)

Обратим внимание, что, согласно (1.17) и (1.20) потенциал притяжения зависит от угловой скорости вращения эллипсоида. Этот парадоксальный факт объясняется тем, что на поверхности эллипсоида (1.14) потенциал Uо силы тяжести должен быть постоянен, и изменение потенциала Qо (1.15) центробежной силы должно компенсироваться изменением потенциала Vо притяжения, как следует из условия (1.16).

Представим (1.17) в виде

. (1.21)

= (1.22)

и разложение(1.19), согласно которому

(1.23)

. (1.24)

Теперь преобразуем потенциал (1.8), записав в явном виде члены с п=0 и 1 и вынесем за скобки член нулевого порядка. Тогда

, (1.25)

где принято во внимание выражение полинома Лежандра второй степени

. (1.26)

Сопоставим потенциалы (1.24) и (1.25). Возьмем произвольную точку на оси Z вращения эллипсоида (рис.1.1). Для точек на оси вращения геоцентрическая широта F совпадает с приведенной широтой u, причем обе они равны p/2, а полуось b совпадает с радиусом-вектором r,

Приравняв потенциалы (1.24) и (1.25) при условии (1.27), находим

. (1.28)

Равенство (1.28) будет выполняться, только если будут равны коэффициенты при одинаковых степенях b. Отсюда следует фундаментальное равенство, устанавливающее связь геометрических параметров эллипсоида с физическими параметрами (стоксовыми постоянными) Земли

(1.29)

Введем в (1.29) безразмерный эксцентриситет е. По определению Е=ае=const, поэтому для отсчетного эллипсоида Е=аоео и (1.29) получает вид

. (1.30)

, . (1.31)

С этими обозначениями напишем

; (1.32)

параметр J2 называют зональный гармонический коэффициент второй степени.

Выясним физический смысл параметров т и J2.Запишем параметр т в виде

(1.33)

Произведение w2ao – это центробежная сила на экваторе уровенного эллипсоида, а — сила притяжения массы М, находящейся в центре эллипсоида, также на его экваторе. Произведение Мао2 представляет собой момент инерции массы М относительно оси вращения эллипсоида. Это максимально возможное значение полярного момента инерции, которое было бы в том случае, если бы вся масса эллипсоида находилась на его экваторе, на расстоянии ао от оси вращения. Таким образом

т – отношение центробежной силы к силе притяжения на экваторе;

J2- отношение разности полярного и экваториального моментов инерции к максимальному моменту инерции.

Равенства (1.29) и (1.32) между геометрическими ао, Е, qо, е и физическими GM, G(C-Am), mJ2 параметрами уровенного эллипсоида точные. Часто используют приближенные соотношения между ними. Если в (1.23) не учитывать отличие между осями эллипсоида, можно принять с точностью порядка сжатия эллипсоида

(1.34)

и для сжатия эллипсоида с учетом зависимости e2»2a

. (1.36)

Параметры, определяющие поле силы тяжести Нормальной Земли, называют фундаментальными геодезическими постоянными. Соотношения между фундаментальными постоянными и методами их определения рассматривают в курсе высшей геодезии.

Введем в (1.8) новые безразмерные коэффициенты J2п по правилу

. (1.37)

Потенциал притяжения примет вид

(1.38)

Этот ряд сходится очень быстро. Его коэффициенты

,

§1.3. ПОТЕНЦИАЛ СИЛЫ ТЯЖЕСТИ УРОВЕННОГО ЭЛЛИПСОИДА

Так как потенциал U силы тяжести равен сумме потенциала V притяжения и потенциала Q центробежной силы, для его определения нужно добавить к (1.17) или (1.38) центробежный потенциал (1.10). Для получения потенциала силы тяжести в эллипсоидальной системе координат b, u выразим в этой системе центробежный потенциал

=. (1.40)

После этого, суммируя (1.17) и (1.40), получаем внешний потенциал силы тяжести уровенного эллипсоида вращения

(1.41)

На поверхности эллипсоида, полагая в (1.41) b=bo, находим

. (1.42)

На любом другом эллипсоиде при b ≠ bo потенциал зависит от широты u. Это означает, что только одна уровенная поверхность U = Uo потенциала силы тяжести является эллипсоидом вращения.

Для нахождения потенциала силы тяжести в полярной сферической системе координат к потенциалу притяжения (1.38) нужно добавить центробежный потенциал(1.10), также выраженный в координатах r,F. После небольших преобразований потенциал силы тяжести будет выглядеть так

. (1.43)

Найдем выражение для потенциала Uо силы тяжести на поверхности эллипсоида. Так как в этом случае потенциал постоянен, для нахождения Uо достаточно вычислить потенциал (1.43) в любой точке эллипсоида. Если выбрать точку на экваторе, то r=aо,Ф=0 и

. (1.44)

Поскольку коэффициенты J2п зависят от J2 и ео, для нахождения потенциала на поверхности уровенного эллипсоида нужно знать постоянные GM, ао, J2, ео.

Таким образом, на поверхности уровенного эллипсоида (Нормальной Земли) потенциал силы тяжести можно найти или по замкнутой формуле (1.42), используя постоянные GM, E,bo,w, или с помощью ряда (1.44), зная GM, ао, J2, ео.

§1.4. СИЛА ТЯЖЕСТИ НА ПОВЕРХНОСТИ УРОВЕННОГО ЭЛЛИПСОИДА

Согласно определению потенциала, сила является производной потенциала. Чтобы найти силу тяжести gо на эллипсоиде, нужно получить производную потенциала U по нормали п к уровенной поверхности эллипсоида

. (1.45)

Знак «минус» в этой формуле означает, что дифференцирование потенциала выполняют по направлению внешней нормали, противоположному направлению силы тяжести.

В системе координат b, u, для силы тяжести можно написать

. (1.46)

После дифференцирования (1.41) можно найти выражение, определяющее нормальную силу тяжести в любой точке эллипсоида. Так как (1.41) содержит только независящие от широты и и поэтому постоянные на поверхности эллипсоида члены и член, содержащий sin2u, производная потенциала на поверхности эллипсоида также должна быть функцией такого же вида, и поэтому можно написать

= Во+ В2 sin2u,

В и Во постоянные, подлежащие определению. На основании двух последних равенств для силы тяжести gр на полюсе эллипсоида при u=p/2 имеем

,

.

Обычно выражают силу тяжести как функцию геодезической широты В, для чего используют известное из курса высшей геодезии соотношение между геодезической В и приведенной и широтами

tgB=Ö1-e2 tgu.

. (1.47)

Формула (1.47) получена в 1929 г. итальянским геодезистом К. Сомильяна(). Ее часто записывают в виде

, (1.48)

. (1.49)

Введем в (1.47) сжатие a уровенного эллипсоида и коэффициент b, равный отношению разности силы тяжести на полюсе и экваторе к силе тяжести на экваторе

. (1.50)

, (1.51)

где b1= . (1.52)

Формулы (1.47)-(1.48) и (1.51) называют формулами распределения нормальной силы тяжести или нормальными формулами. С точностью порядка сжатия формула (1.51) была известна уже Ньютону и Клеро. Член b1sin22B второго порядка относительно сжатия в нормальную формулу включил Гельмерт.

Из формул (1.47)-(1.48) и (1.51) следует, что на поверхности уровенного эллипсоида нормальная сила тяжести не постоянна и зависит от широты. Максимальное значение сила тяжести имеет на полюсе, где

На экваторе сила тяжести минимальна

Увеличение силы тяжести на полюсе объясняется тем, что здесь центробежная сила равна нулю, а из-за сжатия точка на полюсе находится ближе к центру масс Земли по сравнению с точкой на экваторе, что вызывает увеличение силы притяжения. На экваторе центробежная сила максимальна и направлена прямо противоположно силе притяжения.

Изменение силы тяжести вызывает непараллельность уровенных поверхностей нормального поля. Напряженность поля выше на полюсе и здесь расстояние между уровенными поверхностями меньше, чем между этими же поверхностями на экваторе.

Представим согласно (1.45) разность dU потенциалов между эллипсоидом и близкой к нему уровенной поверхностью в виде

H— расстояние между уровенными поверхностями. Дифференцируя при dU постоянном, найдем изменение dH этого расстояния при перемещении вдоль меридиана

dН= .

Используем для нахождения dgо формулу (1.51) и ограничимся только первыми двумя членами правой части

Найдем с помощью этой формулы разность Нр-Не высоты уровенной поверхности на полюсе и экваторе

Нр-Не = .

Для Н=100м Нр-Не =-0,53 м, т. е. уровенная поверхность, проходящая на экваторе на высоте 100 м над эллипсоидом, на полюсе находится на 53 см ниже.

На широте 45о при H=100м и dх= 10км dН=0,8мм. Непараллельность нормальных уровенных поверхностей ощутима при точных нивелировках.

От долготы нормальная сила тяжести не зависит, поэтому при перемещении вдоль параллели расстояние между уровенными поверхностями нормального поля не меняется.

§1.5. НОМАЛЬНАЯ СИЛА ТЯЖЕСТИ ВО ВНЕШНЕЙ ТОЧКЕ. КРИВИЗНА СИЛОВОЙ ЛИНИИ

Формулы (1.47)-(1.48) и (1.51) позволяют получить силу тяжести только на поверхности эллипсоида. Во внешнем пространстве силу тяжести можно найти, дифференцируя выражения (1.17) или (1.38) по нормали к внешней уровенной поверхности. Однако в этом случае уровенная поверхность не является эллипсоидальной и потенциал зависит от широты. Поэтому нормальную силу тяжести вне эллипсоида следует находить из выражения

, (1.56)

h1 и h2 коэффициенты.

Для вычисления нормальной силы тяжести на физической поверхности Земли, вблизи эллипсоида, удобнее использовать ряд Тейлора

, (1.57)

Н – высота точки над эллипсоидом, производные относятся к поверхности эллипсоида. Если ограничиться только первыми членами ряда, для внешней силы тяжести можно написать

. (1.58)

Производную называют вертикальным градиентом нормальной силы тяжести.

Оценим приближенное значение вертикального градиента, приняв за нормальную силу тяжести силу притяжения сферической Земли

.

Для Земли сферической направление высоты Н совпадает с направлением радиуса-вектора r, поэтому для вертикального градиента можно написать

. (1.59)

Вертикальный градиент зависит от расстояния r до центра Земли. На поверхности Земли для средних значений g= 980 гал, r= 6371 км =0,308 мгл/м.

Найдем точное значение градиента на поверхности эллипсоида. Используем прямоугольную топоцентрическую систему координат x, y,z. Если направить ось z по касательной к силовой линии нормального поля, противоположно высоте Н, то вертикальный градиент будет второй производной нормального потенциала

Нормальный потенциал вне эллипсоида удовлетворяет дифференциальному уравнению

, (1.60)

из которого получим

.

Вторые производные потенциала в горизонтальных направлениях связаны с кривизной уровенной поверхности. Если ось х направлена по касательной к меридиану на север, а ось у по касательной к параллели на восток, то

,

M и N – радиусы кривизны меридиана и первого вертикала соответственно. Используя эту формулу, получаем для вертикального градиента силы тяжести на поверхности эллипсоида

. (1.61)

Радиусы кривизны меридиана и первого вертикала определены формулами, известными из курса высшей геодезии

, (1.62)

Оценим величину члена 2w2. Приняв w = 7,292*10-5с-1, получим 2w2=10,6*10-9с-2 или 10,6 Е (Е – этвеш – единица измерения вторых производных потенциала; 1Е=10-9с-2 =1мгл/10км).

Нормальная сила тяжести gо и радиусы кривизны M, N на поверхности эллипсоида изменяются с широтой, поэтому вертикальный градиент также зависит от широты, изменяясь от 3084Е на полюсе до 3088Е на экваторе. Сила тяжести на полюсе медленнее убывает с высотой, чем на экваторе, где, помимо убывания силы притяжения, возрастает пропорционально высоте центробежная сила. Вследствие этого с возрастанием высоты растет разность расстояния между двумя близкими уровенными поверхностями на полюсе и экваторе и сжатие нормальной уровенной поверхности увеличивается. Уровенные поверхности вблизи Нормальной Земли изображены на рис.1.2.

Силовые линии нормального поля

Уровенные поверхности

Рис.1.2. Силовые линии и уровенные поверхности нормального поля вблизи Земли

Уровенные поверхности силовые линии

Приближенно для средних значений силы тяжести и радиусов кривизны

Таким образом, нормальную силу тяжести на высоте Н над эллипсоидом можно найти по формуле

Здесь высота выражена в метрах, сила тяжести в миллигалах. Формула обеспечивает вычисление нормальной силы тяжести с точностью выше 0.1 мгл для высот, меньших 1 км. При более точных вычислениях следует в ряде (1.57) удерживать член, содержащий Н2, и учитывать зависимость градиента (1.63) от широты. На значительных расстояниях от эллипсоида нормальную силу тяжести нужно находить с использованием(1.56).

Для определения кривизны силовой линии нормального поля воспользуемся формулой (1.10). Нормальный потенциал и нормальная сила тяжести не зависят от долготы, поэтому нормальная силовая линия – это плоская кривая, лежащая в плоскости меридиана, и ее кривизна определяется выражением

(1.65)

Силовые линии нормального поля обращены вогнутостью к оси вращения эллипсоида. Наибольшую кривизну они имеют на широте 45о (рис.1.2)

§ 1.6. СИСТЕМА КООРДИНАТ В НОРМАЛЬНОМ ПОЛЕ

нормальная широта Вg – угол между направлением нормальной силы тяжести и плоскостью экватора;

Наряду с геопотенциальным числом в качестве третьей координаты можно использовать высоту в нормальном поле– отрезок нормальной силовой линии от точки Р1 пересечения силовой линии с поверхностью уровенного эллипсоида до точки Р.

Высота и широта в нормальном поле и геодезические широта и высота показаны на рис.1.3. Из-за кривизны нормальной силовой линии широта и высота в нормальном поле отличаются от геодезических. Сравним эти координаты.

Обратимся к рис 1.3. Нормальная широта как внешний угол треугольника Ррр2 равна сумме геодезической широты и угла e между нормалью РРо к эллипсоиду и отвесной линией Рр2. Оценим угол e. Будем считать отрезок Р1Р =НН силовой линии от эллипсоида до точки Р дугой окружности радиуса 1/К. Проведем касательную р1р1¢ к этой окружности в точке Р1 пересечения силовой линии с эллипсоидом; эта касательная является нормалью

e Р

Н e р1¢

НН

Ро Р1

Источник