какие выражения являются целыми

Алгебра. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Алгебраическое выражение, в котором несколько многочленов соединены знаками сложения, вычитания и умножения, называется целым выражением.

Сумма многочленов равна многочлену, членами которого являются все члены этих многочленов.

Разность двух многочленов – это сумма уменьшаемого и многочлена, противоположного вычитаемому.

Произведение одночлена и многочлена равно многочлену, членами которого являются произведения этого одночлена и каждого члена многочлена.

Правило приведения многочлена к стандартному виду:

1)каждый член многочлена привести к стандартному виду;

2)привести подобные члены.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Перед нами несколько выражений, можно ли из них составить общее выражение, соединяя их знаками сложения, вычитания и умножения?

Безусловно. Данные действия мы научились выполнять на предыдущих занятиях.

Одно из выражений, которое может быть получено: (17 + с)(16а – 15х) – (3 + 4ас) + (х + у)

Мы узнаем, как называется полученное выражение, и научимся упрощать подобные выражения.

Начнём с определения.

Алгебраическое выражение, в котором несколько многочленов соединены знаками сложения, вычитания и умножения, называется целым выражением.

Например, полученное при выполнении задания выражение является целым, т.к. многочлены соединены знаками сложения, вычитания и умножения:

(17 + с)(16а – 15х) – (3 + 4ас) + (х + у) – целое выражение.

Выражение, которое содержит многочлены, соединённые знаком деления, не будет являться целым.

Например, выражение (7 + 14а) + (23 – с) : (х + у) – не является целым.

8х + 12 – целое выражение.

Целые выражения можно упрощать, используя правила сложения, вычитания и умножения многочленов.

Во-первых, произведение многочленов равно многочлену, членами которого являются произведения каждого члена одного многочлена и каждого члена другого многочлена Т.е. чтобы найти произведение многочленов, необходимо каждый член одного многочлена умножить на каждый член другого многочлена, а полученные одночлены сложить.

Например, так выполняется умножение многочленов.

(а + с)(х + у) = ах + ау + сх +су

Во-вторых, сумма многочленов равна многочлену, членами которого являются все члены данных многочленов.

Например, так находится сумма многочленов:

(а + с) + (к + х) = а + с + к + х

И, наконец, разность двух многочленов равна многочлену, членами которого являются все члены уменьшаемого и, взятые с противоположными знаками, все члены вычитаемого.

Например, так находится разность двух многочленов.

(а + с) – (к + х) = а + с – к – х

Выражение, полученное в результате выполнения этих действий, нужно приводить к стандартному виду.

Любое целое выражение можно преобразовать в многочлен стандартного вида.

Рассмотрим, как упрощать целое выражение.

Упростите выражение: (17 + с)(16а – 15х) – (3 + 4ас) + (х + у).

Сначала выполним умножение двух первых многочленов, затем раскроем скобки у оставшихся многочленов. Т.к. перед третьей скобкой стоит знак минус, то знаки членов данного многочлена поменяются на противоположные.

(17 + с)(16а – 15х) – (3 + 4ас) + (х + у) = 17 · 16а + 17·(-15)х + 16ас +(-15)сх – 3 – 4ас + х+ у =

Далее приведём полученный многочлен к стандартному виду

= 272а – 255х + 16ас – 15сх – 3 – 4ас + х + у = 272а – 254х + 12ас –15сх + у –3

Итак, сегодня мы получили представление о том, что такое целое выражение, научились его упрощать.

Рассмотрим дополнительно, как доказать, что целое выражение является нулевым многочленом.

Докажите, что целое выражение является нулевым многочленом.

(2х + у)(2х – у) – ( к + 2х)(к – 2х) + (к 2 + у 2 – 8х 2 )

Для доказательства этого утверждения упростим выражение.

Для этого раскроем скобки и приведем к стандартному виду полученное выражение.

Полученный многочлен является нулевым, что и требовалось доказать.

Разбор заданий тренировочного модуля.

Составьте целое выражение по тексту задачи.

Найдите площадь прямоугольника со сторонами (а + с) и (к + х).

Для решения задачи, нужно вспомнить, что площадь прямоугольника находят как произведение двух его смежных сторон. Исходя из условия задачи, площадь находим как (а + с)(к + х). Это и есть искомый ответ.

2. Упростите целое выражение и найдите его степень: 3 · (х + 3)(х – 6) – 5х 2

Вначале упростим целое выражение, используя свойства умножения многочлена на многочлен и одночлена на многочлен. Далее приведём полученный многочлен к стандартному виду, а затем найдём степень полученного многочлена.

Источник

Алгебра. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Алгебраическое выражение, в котором несколько многочленов соединены знаками сложения, вычитания и умножения, называется целым выражением.

Сумма многочленов равна многочлену, членами которого являются все члены этих многочленов.

Разность двух многочленов – это сумма уменьшаемого и многочлена, противоположного вычитаемому.

Произведение одночлена и многочлена равно многочлену, членами которого являются произведения этого одночлена и каждого члена многочлена.

Правило приведения многочлена к стандартному виду:

1)каждый член многочлена привести к стандартному виду;

2)привести подобные члены.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Перед нами несколько выражений, можно ли из них составить общее выражение, соединяя их знаками сложения, вычитания и умножения?

Безусловно. Данные действия мы научились выполнять на предыдущих занятиях.

Одно из выражений, которое может быть получено: (17 + с)(16а – 15х) – (3 + 4ас) + (х + у)

Мы узнаем, как называется полученное выражение, и научимся упрощать подобные выражения.

Начнём с определения.

Алгебраическое выражение, в котором несколько многочленов соединены знаками сложения, вычитания и умножения, называется целым выражением.

Например, полученное при выполнении задания выражение является целым, т.к. многочлены соединены знаками сложения, вычитания и умножения:

(17 + с)(16а – 15х) – (3 + 4ас) + (х + у) – целое выражение.

Выражение, которое содержит многочлены, соединённые знаком деления, не будет являться целым.

Например, выражение (7 + 14а) + (23 – с) : (х + у) – не является целым.

8х + 12 – целое выражение.

Целые выражения можно упрощать, используя правила сложения, вычитания и умножения многочленов.

Во-первых, произведение многочленов равно многочлену, членами которого являются произведения каждого члена одного многочлена и каждого члена другого многочлена Т.е. чтобы найти произведение многочленов, необходимо каждый член одного многочлена умножить на каждый член другого многочлена, а полученные одночлены сложить.

Например, так выполняется умножение многочленов.

(а + с)(х + у) = ах + ау + сх +су

Во-вторых, сумма многочленов равна многочлену, членами которого являются все члены данных многочленов.

Например, так находится сумма многочленов:

(а + с) + (к + х) = а + с + к + х

И, наконец, разность двух многочленов равна многочлену, членами которого являются все члены уменьшаемого и, взятые с противоположными знаками, все члены вычитаемого.

Например, так находится разность двух многочленов.

(а + с) – (к + х) = а + с – к – х

Выражение, полученное в результате выполнения этих действий, нужно приводить к стандартному виду.

Любое целое выражение можно преобразовать в многочлен стандартного вида.

Рассмотрим, как упрощать целое выражение.

Упростите выражение: (17 + с)(16а – 15х) – (3 + 4ас) + (х + у).

Сначала выполним умножение двух первых многочленов, затем раскроем скобки у оставшихся многочленов. Т.к. перед третьей скобкой стоит знак минус, то знаки членов данного многочлена поменяются на противоположные.

(17 + с)(16а – 15х) – (3 + 4ас) + (х + у) = 17 · 16а + 17·(-15)х + 16ас +(-15)сх – 3 – 4ас + х+ у =

Далее приведём полученный многочлен к стандартному виду

= 272а – 255х + 16ас – 15сх – 3 – 4ас + х + у = 272а – 254х + 12ас –15сх + у –3

Итак, сегодня мы получили представление о том, что такое целое выражение, научились его упрощать.

Рассмотрим дополнительно, как доказать, что целое выражение является нулевым многочленом.

Докажите, что целое выражение является нулевым многочленом.

(2х + у)(2х – у) – ( к + 2х)(к – 2х) + (к 2 + у 2 – 8х 2 )

Для доказательства этого утверждения упростим выражение.

Для этого раскроем скобки и приведем к стандартному виду полученное выражение.

Полученный многочлен является нулевым, что и требовалось доказать.

Разбор заданий тренировочного модуля.

Составьте целое выражение по тексту задачи.

Найдите площадь прямоугольника со сторонами (а + с) и (к + х).

Для решения задачи, нужно вспомнить, что площадь прямоугольника находят как произведение двух его смежных сторон. Исходя из условия задачи, площадь находим как (а + с)(к + х). Это и есть искомый ответ.

2. Упростите целое выражение и найдите его степень: 3 · (х + 3)(х – 6) – 5х 2

Вначале упростим целое выражение, используя свойства умножения многочлена на многочлен и одночлена на многочлен. Далее приведём полученный многочлен к стандартному виду, а затем найдём степень полученного многочлена.

Источник

Какие числа называются целыми

Определение целых чисел

Что важно знать о целых числах:

Целые числа на числовой оси выглядят так:

На координатной прямой начало отсчета всегда начинается с точки 0. Слева находятся все отрицательные целые числа, справа — положительные. Каждой точке соответствует единственное целое число.

В любую точку прямой, координатой которой является целое число, можно попасть, если отложить от начала координат данное количество единичных отрезков.

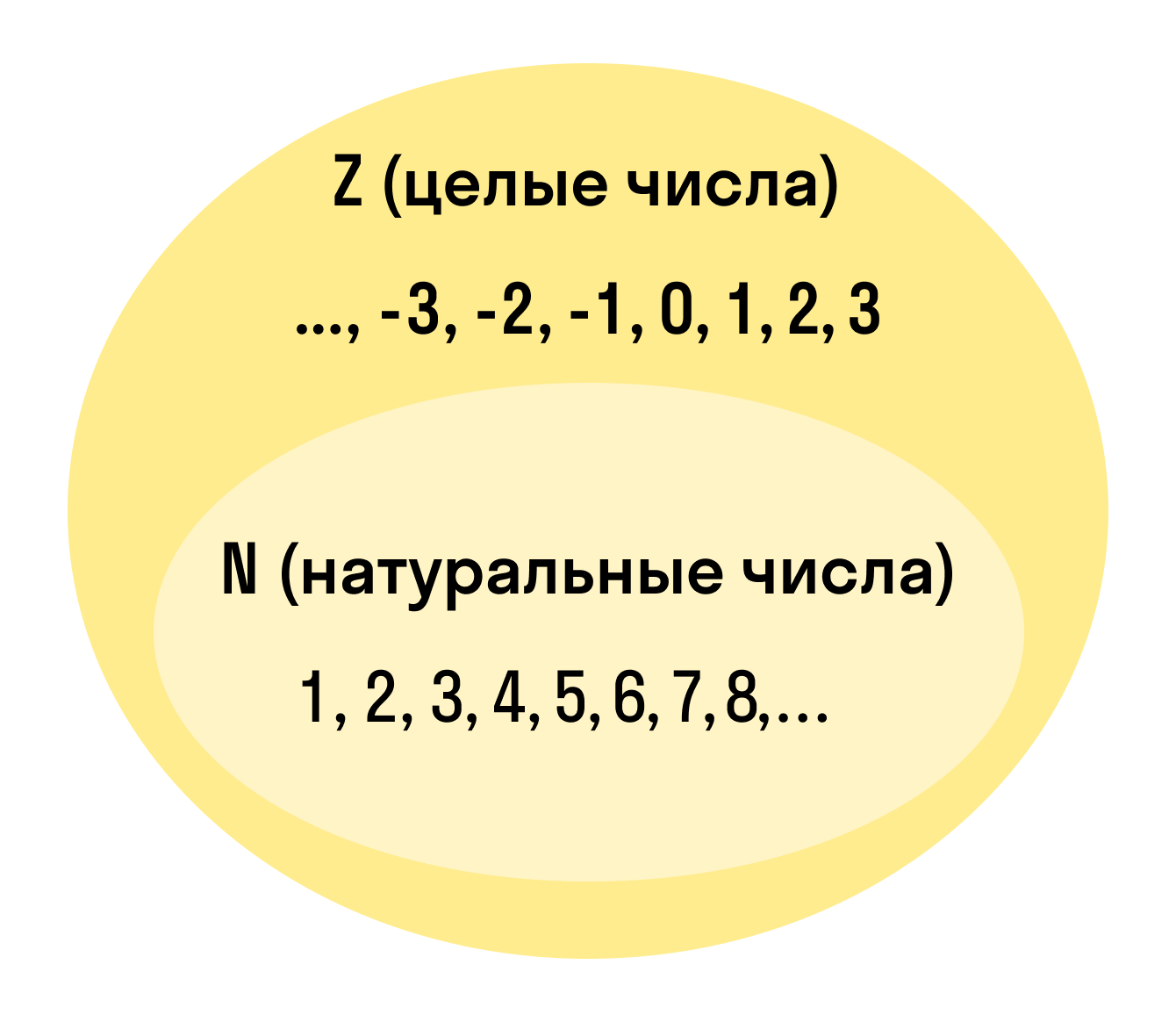
Натуральные числа — это целые, положительные числа, которые мы используем для подсчета. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 + ∞.

Целые числа — это расширенное множество натуральных чисел, которое можно получить, если добавить к ним нуль и отрицательные числа. Множество целых чисел обозначают Z.

Выглядит эти ребята вот так:

Последовательность целых чисел можно записать так:

Свойства целых чисел

Таблица содержит основные свойства сложения и умножения для любых целых a, b и c:

Источник

Целые рациональные выражения

Содержание:

Целые рациональные выражения

Целые рациональные выражения — это рациональные выражения, не содержащие деления на переменные. Целые рациональные выражения состоят из чисел и переменных, соедененных знаками арифметических действий или возведения в целую степень. При этом в знаменателе нет выражений с переменными.

Одночлены и операции над ними

Одночленом называют такое выражение, которое содержит числа, натуральные степени переменных и их произведения. Например, — одночлены, тогда как выражения — не являются одночленами.

Любой одночлен можно привести к стандартному виду, т. е. представить в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных. Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. Сумму показателей степеней всех переменных называют степенью одночлена.

Если между двумя одночленами поставить знак умножения, то получится одночлен, называемый произведением исходных одночленов. При возведении одночлена в натуральную степень также получается одночлен. Результат обычно приводят к стандартному виду.

Приведение одночлена к стандартному виду, умножение одночленов — тождественные преобразования.

Пример 1.

Привести к стандартному виду одночлен

Решение:

Пример 2.

Выполнить умножение одночленов

Решение:

Пример 3.

Возвести одночлен в четвертую степень.

Решение:

Одночлены, приведенные к стандартному виду, называют подобными, если они отличаются только коэффициентом или совсем не отличаются. Подобные одночлены можно складывать и вычитать, в результате чего снова получается одночлен, подобный исходным (иногда получается 0). Сложение и вычитание подобных одночленов называют приведением подобных членов.

Пример 4.

Выполнить сложение одночленов

Решение:

Многочлены. Приведение многочленов к стандартному виду

Многочленом называют сумму одночленов. Если все члены многочлена записать в стандартном виде (см. п. 51) и выполнить приведение подобных членов, то получится многочлен стандартного вида.

Всякое целое выражение можно преобразовать в многочлен стандартного вида — в этом состоит цель преобразований (упрощений) целых выражений.

Пример 1.

Привести многочлен к стандартному виду.

Решение:

Сначала приведем к стандартному виду члены многочлена.

Получим После приведения подобных членов получим многочлен стандартного вида

Пример 2.

Привести многочлен к стандартному виду.

Решение:

Если перед скобками стоит знак плюс, то скобки можно опустить, сохранив знаки всех слагаемых, заключенных в скобки. Воспользовавшись этим правилом раскрытия скобок, получим

Пример 3.

Решение:

Если перед скобками стоит знак минус, то скобки можно опустить, изменив знаки всех слагаемых, заключенных в скобки. Воспользовавшись этим правилом раскрытия скобок, получим

Пример 4.

Решение:

Произведение одночлена и многочлена равно сумме произведений этого одночлена и каждого члена многочлена:

Пример 5.

Решение:

Имеем

Пример 6.

Решение:

Имеем

Осталось привести подобные члены (они подчеркнуты). Получим

Формулы сокращенного умножения

В некоторых случаях приведение целого выражения к стандартному виду многочлена осуществляется с использованием тождеств:

Эти тождества называют формулами сокращенного умножения.

Рассмотрим примеры, в которых нужно преобразовать заданное выражение в многочлен стандартного вида.

Пример 1.

Решение:

Воспользовавшись формулой (1), получим

Пример 2.

Решение:

Пример 3.

Решение:

Воспользовавшись формулой (3), получим

Пример 4.

Решение:

Воспользовавшись формулой (4), получим

Разложение многочленов на множители

Иногда можно преобразовать многочлен в произведение нескольких множителей — многочленов или одночленов. Такое тождественное преобразование называют разложением многочлена на множители. В этом случае говорят, что многочлен делится на каждый из этих множителей.

Рассмотрим некоторые способы разложения многочленов на множители.

1. Вынесение общего множителя за скобки. Это преобразование является непосредственным следствием распределительного закона

Пример 1.

Разложить на множители многочлен

Решение:

Обычно при вынесении общего множителя за скобки каждую переменную, входящую во все члены многочлена, выносят с наименьшим показателем, который она имеет в данном многочлене. Если все коэффициенты многочлена — целые числа, то в качестве коэффициента общего множителя берут наибольший по модулю общий делитель всех коэффициентов многочлена.

2. Использование формул сокращенного умножения. Формулы (1) — (7) из п. 53, будучи прочитанными «справа налево», во многих случаях оказываются полезными для разложения многочленов на множители.

Пример 2.

Разложить на множители

Решение:

Имеем Применив формулу (1) (разность квадратов), получим Применив теперь формулы (4) и (5) (сумма кубов, разность кубов), получим

Пример 3.

Решение:

Сначала вынесем за скобки общий множитель. Для этого найдем наибольший общий делитель коэффициентов 4, 16, 16 и наименьшие показатели степеней, с которыми переменные а или Ь входят в составляющие данный многочлен одночлены. Получим

Так как, далее, по формуле (2), то окончательно получаем

3. Способ группировки. Он основан на том, что пе-реместительный и сочетательный законы сложения позволяют группировать члены многочлена различными способами. Иногда удается такая группировка, что после вынесения за скобки общих множителей в каждой группе в скобках остается один и тот же многочлен, который в свою очередь как общий множитель может быть вынесен за скобки.

Рассмотрим примеры разложения многочлена на множители способом группировки

Пример 4.

Решение:

Произведем группировку следующим образом:

Пример 5.

Решение:

Пример 6.

Решение:

Здесь никакая группировка не приведет к появлению во всех группах одного и того же многочлена. В таких случаях иногда оказывается полезным представить какой-либо член многочлена в виде некоторой суммы, после чего снова попробовать применить способ группировки. В нашем примере целесообразно представить в виде суммы Получим

Пример 7.

Решение:

Прибавим и отнимем одночлен

Получим

Здесь применен метод выделения полного квадрата.

Многочлены от одной переменной

Многочлен , где — числа (), a х — переменная, называют многочленом первой степени; многочлен где — числа (), а х — переменная, называют многочленом второй степени или квадратным трехчленом; многочлен где — числа (), a х — переменная, называют многочленом третьей степени.

Вообще если — числа (), а х — переменная, то многочлен

называют многочленом п-й степени (относительно х); — члены многочлена, — коэффициенты, — старший член многочлена, — коэффициент при старшем члене, — свободный член многочлена. Обычно многочлен записывают по убывающим степеням переменной, т. е. степени переменной х постепенно уменьшаются, в частности на первом месте стоит старший член, на последнем — свободный член. Степень многочлена — это степень старшего члена.

Например, — многочлен пятой степени, в котором — старший член, 1 — свободный член многочлена.

Если коэффициент при старшем члене равен 1, то многочлен называют приведенным, если указанный коэффициент отличен от 1, то неприведенным.

Корнем многочлена Р(х) называют такое значение х, при котором многочлен обращается в нуль. Например, число 2 является корнем многочлена так как

Разложение квадратного трехчлена на линейные множители

Если — корни квадратного трехчлена (т. е. корни уравнения = 0), то

Эта формула применяется для разложения квадратного трехчлена на множители.

Пример:

Разложить на множители

Решение:

Применив формулу корней квадратного уравнения (см. п. 137) к уравнению , находим Значит,

Разложение на множители двучлена

Если перемножить многочлены то получим

Обобщением формул (1), (2), (3) является формула разложения на множители двучлена

Если, в частности, = 1, то получаем

Например,

Возведение двучлена в натуральную степень (бином Ньютона)

В этом пункте речь идет о том, как двучлен (или бином) возвести в любую натуральную степень.

Воспользовавшись тем, что можно вывести формулу

Вообще справедлива следующая формула (бином Ньютона):

Пример:

Для по формуле бинома Ньютона получаем

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник