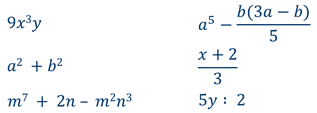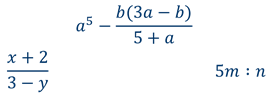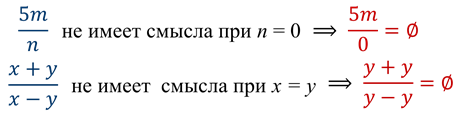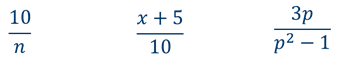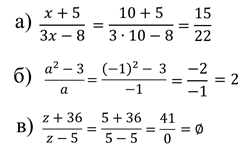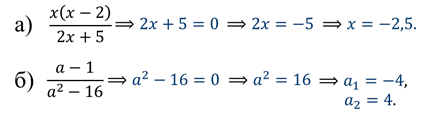какие выражения целые а какие дробные

Виды рациональных выражений

Целое выражение – это математическое выражение, составленное из чисел и буквенных переменных с помощью действий сложения, вычитания и умножения. Также к целым относятся выражения, которые имеют в своем составе деление на какое либо число, отличное от нуля.

Примеры целого выражения

Ниже представлены несколько примеров целых выражений:

Дробные выражения

Если же в выражении присутствует деление на переменную или на другое выражение содержащее переменную, то такое выражение не является целым. Такое выражение называется дробным. Дадим полное определение дробного выражения.

Примеры дробных выражений:

Дробные и целые выражения составляют два больших множества математических выражений. Если эти множества объединить, то получим новое множество, которое называется рациональными выражениями. То есть рациональные выражения это все целый и дробные выражения.

Нам известно, что целые выражения имеют смысл при любых значениях переменных, которые в него входят. Это следует из того, что для нахождения значения целого выражения необходимо выполнять действия, которые всегда возможны: сложение, вычитание, умножение, деление на число отличное от нуля.

Дробные же выражения, в отличии от целых, могут и не иметь смысла. Так как присутствует операция деления на переменную или выражение содержащее переменные, и это выражение может обратится в нуль, а делить на нуль нельзя. Значения переменных, при которых дробное выражение будет иметь смысл, называют допустимыми значениями переменных.

Рациональная дробь

Одним из частных случаев рациональных выражений будет являться дробь, числитель и знаменатель которой многочлены. Для такой дроби в математике тоже существует свое название – рациональная дробь.

Рациональная дробь будет иметь смысл в том случае, если её знаменатель не равен нулю. То есть допустимыми будут являться все значения переменных, при которых знаменатель дроби отличен от нуля.

Источник

Рациональные выражения

Урок 1. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Рациональные выражения»

На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Целые и дробные выражения называют рациональными выражениями.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Дробное выражение при некоторых значениях переменных может не иметь смысла.

Чтобы найти значение рационального выражения, надо:

1) подставить числовое значение переменной в данное выражение;

2) выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.

Как вы уже знаете, выражение вида называется дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Найдите значение дроби.

Найдите допустимые значения переменной в выражениях:

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Чтобы найти значение рационального выражения, надо:

1) Подставить числовое значение переменной в данное выражение;

2) Выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.

Источник

Алгебра. 8 класс

Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля.

Дробные выражения – это выражения, которые помимо действий сложения, вычитания, умножения и деления на число, отличное от нуля, содержат деление на выражение с переменными.

Целые и дробные выражения вместе называют рациональными выражениями.

Дробь – это выражение вида .

Целое выражение имеет смысл при любых значениях входящих в него переменных, потому что действия для нахождения значения целого выражения, всегда возможны.

Дробное выражение при некоторых значениях переменной может не иметь смысла.

• не имеет смысла при x = 0.
• не имеет смысла при x = y.

Дробные выражения имеют смысл при любых значениях входящих в них переменных, кроме тех, что обращают знаменатель в нуль.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Примеры

В рациональной дроби допустимыми являются те значения переменных, при которых не обращается в нуль знаменатель дроби.

Чтобы найти допустимые значения переменных в дроби, необходимо:

• Приравнять знаменатель, содержащий переменные, к нулю.
• Решить полученное уравнение. Корни этого уравнения будут являться теми значениями переменных, которые обращают знаменатель в нуль.
• Исключить эти значения из всех действительных чисел.

Пример 1.
Найти допустимые значения переменной в дроби .

1) x(x + 1) = 0
2) x = 0 или x + 1 = 0
x = 0 или x = –1.
Корни уравнения 0 и – 1.
3) Допустимыми значениями x являются все числа, кроме 0 и –1.

Пример 2.
Найти значения x, при которых дробь равна нулю.

, когда x 2 – 1 = 0 и x + 1 ≠ 0.
1) x 2 – 1 = 0
2) (x – 1)(x + 1) = 0
x = ±1
3) x + 1 ≠ 0
x ≠ –1.
при x = 1.

Алгебра. 8 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. – 6-е изд. – М.: Просвещение, 2017.

Источник