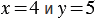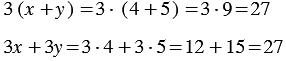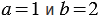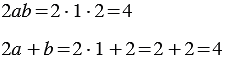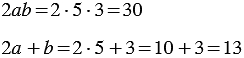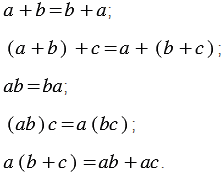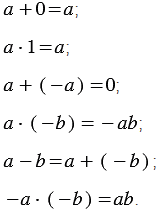какие выражения называются тождественно равными
Тождественно равные выражения: определение, примеры
После того, как мы разобрались с понятием тождеств, можно переходить к изучению тождественно равных выражений. Цель данной статьи – объяснить, что это такое, и показать на примерах, какие выражения будут тождественно равными другим.
Тождественно равные выражения: определение
Понятие тождественно равных выражений обычно изучается вместе с самим понятием тождества в рамках школьного курса алгебры. Приведем основное определение, взятое из одного учебника:
Тождественно равными друг другу будут такие выражения, значения которых будут одинаковы при любых возможных значениях переменных, входящих в их состав.
Также тождественно равными считаются такие числовые выражения, которым будут отвечать одни и те же значения.
Это достаточно широкое определение, которое будет верным для всех целых выражений, смысл которых при изменении значений переменных не меняется. Однако позже возникает необходимость уточнения данного определения, поскольку помимо целых существуют и другие виды выражений, которые не будут иметь смысла при определенных переменных. Отсюда возникает понятие допустимости и недопустимости тех или иных значений переменных, а также необходимость определять область допустимых значений. Сформулируем уточненное определение.
Тождественно равные выражения – это те выражения, значения которых равны друг другу при любых допустимых значениях переменных, входящих в их состав. Числовые выражения будут тождественно равными друг другу при условии одинаковых значений.
Фраза «при любых допустимых значениях переменных» указывает на все те значения переменных, при которых оба выражения будут иметь смысл. Это положение мы объясним позже, когда будем приводить примеры тождественно равных выражений.
Можно указать еще и такое определение:
Тождественно равными выражениями называются выражения, расположенные в одном тождестве с левой и правой стороны.
Примеры выражений, тождественно равных друг другу
Используя определения, данные выше, рассмотрим несколько примеров таких выражений.
Для начала возьмем числовые выражения.
Так, 2 + 4 и 4 + 2 будут тождественно равными друг другу, поскольку их результаты будут равны ( 6 и 6 ).
Но область допустимого значения в одном выражении может отличаться от области другого.
Если мы заменяем одно выражение на другое, которое является тождественно равным ему, то этот процесс называется тождественным преобразованием. Это понятие очень важно, и подробно о нем мы поговорим в отдельном материале.
Тождество. Тождественные преобразования. Примеры.
Тождества в основном применяются для решения линейных уравнений.
Тождеством называется равенство, которое верно при всех значениях переменных.
Или другими словами, тождество — это равенство, которое выполняется на всём множестве значений переменных, входящих в него, например:
В этих выражениях при всех значениях a и b равенство верное.
2 выражения с равными значениями при всех значениях переменных являются тождественно равными.
Равенство x+2=5 может существовать не при всех значениях x, а лишь при x=3. Это равенство не будет тождеством, это будет уравнением. Кроме того, тождеством будет равенство, которое не содержит переменные, например 25 2 =625.
Тождественное равенство обозначают символом «≡» (тройное равенство).
Примеры тождеств.
— Тождество Эйлера (кватернионы);
— Тождество Эйлера (теория чисел);
— Тождество четырёх квадратов;
— Тождество восьми квадратов;
Тождественные преобразования.
Тождественное преобразование выражения (преобразование выражения) – это подмена одних выражений другими, тождественно равными друг другу.
Для тождественных преобразований используют формулы сокращенного умножения, законы арифметики и другие тождества.
Выполним тождественные преобразования с такой дробью: 
Полученное тождество, при х ≠ 0 и х ≠ 1 (недопустимые значения), т.к. знаменатель левой части не может быть равен нулю.
Доказательство тождеств.
Для того, чтоб доказать тождество нужно сделать тождественные преобразования обеих или одной части равенства, и получить слева и справа одинаковые алгебраические выражения.
Например, доказать тождество:
Вынесем х за скобки:
Это равенство есть тождество, при х≠0 и х≠1.
Чтоб доказать, что равенство не является тождеством, нужно найти 1-но значение переменной (которое допустимо) у которой числовые выражения (которые были получены) станут не равными друг другу.
5−1 ≠ 5+1 — подставим, к примеру, 5.
Это равенство не тождество.
Разница между тождеством и уравнением.
Тождество верно при всех значениях переменных, а уравнение – это равенство, которое верно только при одном либо нескольких значениях переменной.
Это выражение верно лишь при х = 10.
Тождеством будет равенство, которое не содержит переменных.
Тождественно равные выражения. Тождества
| Два выражения, значения которых равны при любых значениях переменных, называют тождественно равными. |
Рассмотрим две пары выражений:
1) 
Найдем их значения при
Мы получили один и тот же результат. Из распределительного свойства следует, что вообще при любых значениях переменных 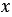
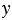

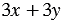
2)
Найдем их значения при
Мы получили один и тот же результат. Однако, можно указать такие значения 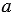
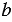
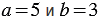
Мы получили разные результаты.
Следовательно, выражения 
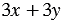
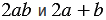
| Равенство, верное при любых значениях переменных, называется тождеством. |
Равенство 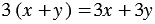
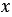
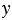
Также к тождествам можно отнести равенства, выражающие свойства сложения и умножения чисел:
Можно привести и другие примеры тождеств:
Тождествами считают и верные числовые равенства.
Очень часто при вычислении значений выражений, легче сначала упростить имеющееся выражение, а затем выполнять вычисления.
| Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. |
К тождественным преобразованиям можно отнести приведение подобных слагаемых и раскрытие скобок.
Примеры:
1) 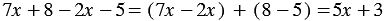
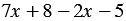
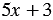
2) 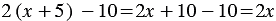
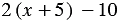
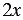
Для того, чтобы доказать, что данное равенство является тождеством (или доказать тождество), используют следующие методы:
1) тождественно преобразуют одну из частей данного равенства, получая другую часть;
2) тождественно преобразуют каждую из частей данного равенства, получая одно и то же выражение;
3) доказывают, что разность левой и правой частей данного равенства тождественно равна нулю.
Также, чтобы доказать, что равенство не является тождеством, достаточно привести контрпример, т.е. указать такое значение переменной (или переменных, если их несколько), при котором данное равенство не выполняется.
Пример: Докажите, что равенство 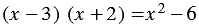
Решение: Приведем контрпример. Если 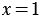
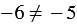
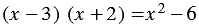
Поделись с друзьями в социальных сетях:
Знак тождества в математике
Вы будете перенаправлены на Автор24
Тождественность в математике — очень часто используемое понятие. Различают понятия тождественных равенств, тождественных выражений и тождественных преобразований, давайте более подробно разберём, что значит каждое из этих понятий.
Тождественные выражения в математике
Рассмотрим три простых алгебраических выражения:
Мы подходим непосредственно к определению тождественных выражений:
Выражения называются тождественными друг с другом, если при любых значениях переменных они всегда равны между собой.
При значении игрека, равному двум, первое из этих двух выражений теряет смысл, так как на нуль делить нельзя, а в знаменателе при этом значении получается нуль.
Понятия «тождество» и «тождественное равенство»
Готовые работы на аналогичную тему
Что же такое тождество в алгебре?
Тождество в математике — это равенство, которое всегда выполняется или, иными словами, является справедливым для всех множеств значений его переменных.
Если два и более тождественных выражения записать непосредственно рядом друг с другом через знак «равно» — то получится тождественное равенство, то есть тождество.
Знак тождества в математике
Чаще всего тождества записывают через знак «равно» — «$=$», знак «тождественно» — «≡» иногда используют для особого выделения в речи тождественности какого-либо равенства. Обычно знак тождества используется значительно реже, чем знак равенства.
Тождественные преобразования
Очень часто для того чтобы упростить процесс вычисления каких-либо выражений, а также для их сравнения и более удобной подстановки переменных в равенства используют различные математические преобразования. Эти преобразования называются тождественными преобразованиями, так как они не изменяют конечные значения выражений и равенств.
Тождественные преобразования — это преобразования и замены одного выражения другим, тождественным ему, не изменяющие конечное значение выражений и не приводящие к нарушению тождественности равенств.
Любое выражение при любых допустимых значениях переменных, используемых в нём, принимает какое-либо значение. Из этого можно сделать вывод, что применение различных законов, соблюдающихся для арифметических действий приводит к преобразованию исходного выражение в новое, тождественное первоначальному выражению.
Какие выражения тождественны?
Ответ:
Тождественными являются выражения под номером 2 и 3, в случае выражений под номером 2 слева дана сокращённая формула разности квадратов, а справа — развёрнутая. В случае третьего выражения нужно упростить выражение справа:
Тождественные преобразования выражений
п.1. Соответственные значения
Рассмотрим два выражения с переменными:
Вычислим их значения при x=2:
Числа 16 и 2 называются соответственными значениями выражений f(x)и g(x) при одинаковом значении x=2. В данном случае соответственные значения не равны. Теперь подставим x=3:
Соответственные значения равны.
Соответственные значения двух выражений, содержащих одни и те же переменные – это числовые значения этих выражений, полученные при подстановке одинаковых значений переменных.
Соответственные значения могут быть:
п.2. Область допустимых значений
Ограничения на ОДЗ определяются видом выражения:
Тождество – формула, в которой два тождественных выражения соединены знаком равенства.
Согласно определению, тождество – это равенство, которое является истинным при всех допустимых значениях переменных, входящих в него.
Тождествами также принято считать истинные числовые равенства.
Разница между тождеством и уравнением заключается в том, что тождество является истинным при всех допустимых значениях переменных, а уравнения – только для одного или нескольких значений переменных из ОДЗ.
Тождественное преобразование выражений – это замена одного выражения другим, тождественно ему равным.
Для доказательства (или опровержения) тождеств используют следующие алгоритмы.
Алгоритм доказательства, что равенство является тождеством
1. Выполнить тождественные преобразования одной или обеих частей равенства.
2. Сравнить полученные слева и справа алгебраические выражения. Если они одинаковы, то равенство является тождеством.
Если выражения неодинаковы, продолжить тождественные преобразования или перейти к доказательству того, что равенство не является тождеством.
Алгоритм доказательства, что равенство не является тождеством
Найти хотя бы одно значение переменной, при котором соответственные значения выражений слева и справа неравны.
п.4. Примеры
Пример 1. Докажите тождество 3(x+1)-2(x-1)-x=5(x+1)-5x
● Тождественные преобразования левой части:
Тождественные преобразования правой части:
Получаем: 5=5. Равенство является тождеством.
Что и требовалось доказать. ○
Пример 2. Тождественны ли выражения 1-(1-(1-b)) и 1-b?
Тождественные преобразования левой части:
Получаем: 1-b=1-b. Выражения тождественны.
Пример 3. Верно ли тождество |x|+1=|x+1|?
Найдем соответственные значения левой и правой части при x=-1.
Равенство не является тождеством.
Пример 4. Является ли тождеством равенство |a+b|=|a|+|b|?
Найдем соответственные значения левой и правой части при a=-1, b=1.