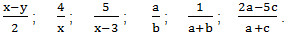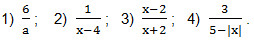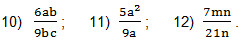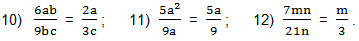какие выражения называются алгебраическими

Математические термины

Алгебра — это наука, изучающая действия над числовыми и буквенными величинами. Кроме того, она занимается решениями уравнений и связанными с ними действиями. Под буквенными величинами обычно понимают конкретные или переменные числовые значения. Входящие в состав записи буквы могут иметь различные числовые величины. Например, в формуле S * 4 + 12 символом S может быть заменена известная или неизвестная величина или даже целое выражение.

Математики под алгебраическим выражением понимают запись, составленную со смыслом, состоящую из букв и цифр, обозначающих числа. При этом она может содержать скобки и знаки арифметических действий. Исходя из этого простейшего определения можно утверждать, что формулы 2 * k — s, 4 * (y — 3/2), 0,89 * a — g * (9a + 4b), a 2 и (29p — 56) / log (a + c) являются примерами алгебраических выражений. Так как буквы в записях обозначают различные числа, то их считают переменными, а само уравнение — выражением с переменной.

Если же значение переменной известно и его можно подставить на место буквенного обозначения, то результат, полученный после выполнения указанных в уравнении действий, называется ответом алгебраического выражения. Но если число, подставляемое вместо буквы, приводит к бессмысленности записи, то оно считается недопустимым. Из этого можно сделать вывод, что одна и та же алгебраическая запись при различных величинах букв может иметь отличные значения.

На практике приходится сталкиваться с довольно сложными и громоздкими алгебраическими выражениями, поэтому над ними приходится выполнять ряд действий, правил, законов или использовать свойства для упрощения записи.

Кроме определений здесь применяется понятие «тождественность». Под ним понимают два выражения, для которых при любых значениях переменных, входящих в их состав, будет справедливо их равенство, например, 56* (x+с) = 56 * x + 56 * с.

Эти два выражения можно заменить друг другом или, выражаясь математическим языком, — «выполнить тождественное преобразование».

Виды выражений

В школе на уроках алгебры приходится сталкиваться с различными видами выражений. Обычно они состоят из нескольких членов. В математике существует группирование, объединяющее сходные элементы. Обучение понятиям начинают в седьмом классе с того, что приводят следующие определения:

Многочлен всегда подразумевает выполнение действий. При описании понятия используют и такие термины, как коэффициент, член, степень. Во время работы с одночленами применяют тождественное их приведение к стандартному виду.

В нём выражение представляют как произведение числового множителя и натуральной степени разных переменных, например, 2 * a, −x * 3.

Выражения в алгебре могут быть следующих видов:

Все указанные виды относят к простым, но с 7 класса алгебраические выражения будут усложняться. Сложный вид записи обычно состоит из многочлена, включающего в себя извлечение корня, логарифмы и возведение в степень, например, ln (x 2 — 1) * tg ((x + p) / cos x). И хоть среди них попадаются перечисленные типы, их относят к общему виду.

Вычисление сложных выражений подразумевает выполнение преобразований, которые позволят проще решить задание и найти правильный ответ.

Алгебраические действия

Решая задачу, приходится выполнять те или иные преобразования. Чаще всего сложность задания определяется громоздкостью и объёмом соответствующих преобразований, поэтому в школе на уроках элементарной математики часто попадаются задачи на упрощения.

Основу всех алгебраических действий составляют три закона. Это правила, касающиеся сложения и умножения: переставное, соединительное и распределительное. Но наряду с ними применяют и формулы сокращённого умножения.

На начальном этапе обучения рекомендуется даже записать данные правила отдельно на листик и пользоваться им, пока применение законов не дойдёт до автоматизма. Вот некоторые практические рекомендации, решаться с которыми примеры будут намного легче:

Не стоит забывать и о такой операции, как деление многочлена. Для этого используют метод столбика. Заключается он в размещении слагаемых многочлена в порядке убывания степени переменной и разделения первого слагаемого числителя многочлена на первое слагаемое знаменателя.

Затем результат умножают на делитель и отнимают ответ от делимого.

Применение преобразований

Алгебраические выражения, показывающие, что одна величина больше другой или равна ей, называют уравнениями и равенствами. При этом их используют для составления формул, то есть для записи, выражающей зависимость между двумя или несколькими переменными. Это удобно, так как преобразования позволяют привести формулу к простому для запоминания виду.

При решении примеров важно знать все существующие методы. Какой из них применять, конкретно указать нельзя, всё зависит от личных предпочтений и опыта решения подобных заданий. Например, пусть нужно упростить сложное выражение (a 3 (b — c) + b 3 (c — a) + c 3 (a — b)) / (a 2 (b — c) + b 2 (c — a) + c 2 (a — b)).

Сначала можно попробовать разложить на множители делитель и делимое. Один из вариантов преобразования числителя следующий:

a 3 (b — c) + b 3 (c — a) + c 3 (a — b) = a 3 b — b 3 c — a 3 c + b 3 c + c 3 (a — b) = ab (a 2 — b 2 ) = ab (a 2 — b 2 ) — c (a 3 — b 3 ) + c 3 (a — b) = (a — b) (ab (a + b) — c (a 2 + ab + b 2 ) + c 3 = (a — b) (a 2 b — a 2 c + ab 2 — abc + c 3 — cb 2 ) = (a — b) (a 2 (b — c) + ab (b — c) — c (b 2 — c 2 ) = (a — b) (b — c) (a 2 — c 2 + ab — cb) = (a — b) (b — c) (a — c) (a + b + c).

По аналогии раскладывая знаменатель, можно прийти к результату: (a — b) (b — c) (a — c). В итоге получится равенство (a 3 (b — c) + b 3 (c — a) + c 3 (a — b)) / (a 2 (b — c) + b 2 (c — a) + c 2 (a — b)) = ((a — b) (b — c) (a — c) (a + b + c)) / ((a — b)(b — c)(a — c)) = a + b + c.

В числителе возможно выделить множитель (a — b) на том основании, что делимое равно нулю, когда a совпадает с b. Обычно в двух взаимно обратных операциях выполнение одной сложнее, чем другой. Это касается, в частности, выполнения умножения алгебраических выражений и разложения на множители или возведения в степень с извлечением корня. Например, легко увидеть, что (5 + 3 √2) 2 = 43 + 30 √2, но значительно труднее прочитать это равенство справа налево.

Следует помнить, что когда при решении задачи встречается выражение подкоренного вида √с + n * √k или √a + b√k, то необходимо попытаться добыть соответствующий корень. Если же это невозможно, то нужно воспользоваться подбором.

Если нужно упростить выражение √11 + 6 √ 2, то его можно представить как c + b √2. Следовательно, справедливо будет следующее равенство: 11 + 6 √2 = с 2 + 2b 2 + 2 cb √2. Поиск целых (рациональных) c и b приведёт к решению системы: a 2 + 2b 2 = 11, ab = 3.

При этом подобрать нужную пару целых легко: a = 3, b = 1, то есть можно записать равенство как √11 + 6√ 2 = 3 + √2.

Источник

Алгебраические выражения

Алгебраическое выражение — это запись, составленная со смыслом, в которой числа могут быть обозначены и буквами, и цифрами. Также она может содержать знаки арифметических действий и скобки.

Любую букву, обозначающую число, и любое число, изображённое с помощью цифр, принято считать в алгебре также алгебраическим выражением.

Алгебраические выражения, входящие в состав формул, могут применяться к решению частных арифметических задач, если в них заменить буквы данными числами и произвести указанные действия. Число, которое получится, если взять вместо букв какие-либо числа и произвести над ними указанные действия, называется численной величиной алгебраического выражения. Из этого легко сделать вывод, что одно и то же алгебраическое выражение при различных значениях входящих в него букв может иметь различные числовые величины.

при a = 2, m = 5, b = 1, n = 4 вычисляется:

а при a = 3, m = 4, b = 5, n = 1 вычисляется:

3 · 4 + 5 · 1 = 17 и т. д.

при a = 1, b = 2, c = 3 равно:

а при a = 2, b = 3, c = 4 равно:

Коэффициент

Коэффициент — это числовой множитель алгебраического выражения, представляющего собой произведение нескольких сомножителей. Коэффициент в выражении ставится перед всеми остальными буквенными множителями. Таким образом,

произведение чисел a, b, c, d, 4 записывается так: 4abcd;

произведение чисел m, n, , p записывается так: .

Числа 4 и — это коэффициенты. Очевидно, что

.

Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым.

Если в алгебраическом выражении нет числового множителя, то подразумевается, что коэффициент равен единице, так как

Виды выражений

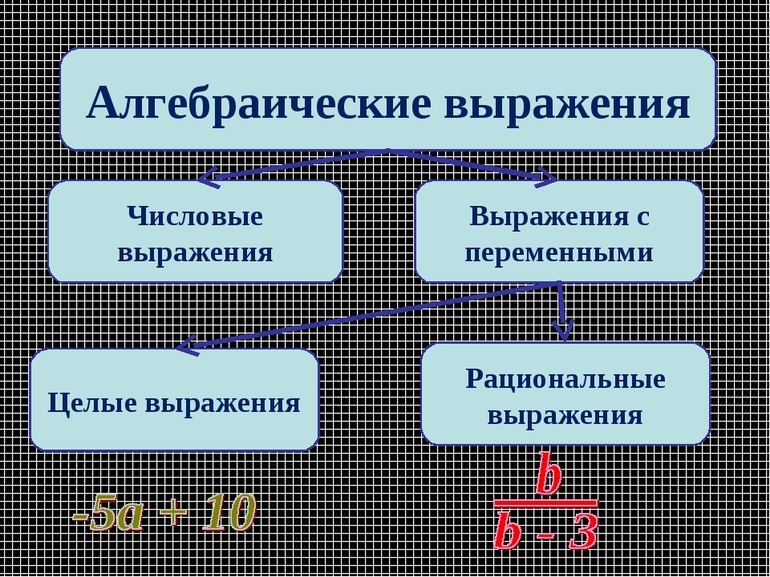
Алгебраическое выражение, в которое не входят буквенные делители, называется целым, в противном случае дробным или алгебраической дробью.

Целые алгебраические выражения:

Дробные алгебраические выражения:

Выражения, не содержащие корней, называются рациональными, а содержащие корни — иррациональными или радикальными. Например, все выражения, приведённые выше, являющиеся целыми или дробными, так же можно назвать и рациональными.

Источник

Основные виды выражений в алгебре

Уроки алгебры знакомят нас с различными видами выражений. По мере поступления нового материала выражения усложняются. При знакомстве со степенями они постепенно добавляются в выражение, усложняя его. Также происходит с дробями и другими выражениями.

Чтобы изучение материала было максимально удобным, это производится по определенным названиям для того, чтобы можно было их выделить. Данная статья даст полный обзор всех основных школьных алгебраических выражений.

Одночлены и многочлены

Выражения одночлены и многочлены изучаются в школьной программе, начиная с 7 класса. В учебники были даны определения такого вида.

Одночлены – это числа, переменные, их степени с натуральным показателем, любые произведения, сделанные с их помощью.

Многочленами называют сумму одночленов.

Чтобы отличать одночлен от многочлена, обращают внимание на степени и их определения. Немаловажно понятие коэффициента. При приведении подобных слагаемых их разделяют на свободный член многочлена или старший коэффициент.

Над одночленами и многочленами чаще всего выполняются какие-то действия, после которых выражение приводится к вижу одночлена. Выполняется сложение, вычитание, умножение и деление, опираясь на алгоритм для выполнения действий с многочленами.

Когда имеется одна переменная, не исключено деление многочлена на многочлен, которые представляются в виде произведения. Такое действие получило название разложение многочлена на множители.

Рациональные (алгебраические) дроби

Понятие рациональные дроби изучаются в 8 классе средней школы. Некоторые авторы называют их алгебраическими дробями.

Рациональной алгебраической дробью называют дробь, в которой на месте числителя и знаменателя выступают многочлены или одночлены, числа.

Алгебраические дроби можно складывать, вычитать, умножать, делить, возводить в степень. Подробнее это рассматривается в разделе действий с алгебраическими дробями. Если необходимо преобразовать дробь, нередко пользуются свойством сокращения и приведения к общему знаменателю.

Рациональные выражения

В школьном курсе изучается понятие иррациональных дробей, так как необходима работа с рациональными выражениями.

Рациональные выражения считаются числовыми и буквенными выражениями, где используются рациональные числа и буквы со сложением, вычитанием, умножением, делением, возведением в целую степень.

Рациональные выражения могут не иметь знаков, принадлежащих функции, которые приводят к иррациональности. Рациональные выражения не содержат корней, степеней с дробными иррациональными показателями, степеней с переменными в показателе, логарифмических выражений, тригонометрических функций и так далее.

Все рациональные выражения подразделяют на целые и дробные.

Целые рациональные выражения

Целые рациональные выражения – это такие выражения, не содержащие деления на выражения с переменными отрицательной степени.

Дробные рациональные выражения

Дробное рациональное выражение – это выражение, которое содержит деление на выражение с переменными отрицательной степени.

Выражения со степенями

Выражения, которые содержат степени в любой части записи, называют выражениями со степенями или степенными выражениями.

Иррациональные выражения, выражения с корнями

Корень, имеющий место быть в выражении, дает ему иное название. Их называют иррациональными.

Иррациональными выражениями называют выражения, которые имеют в записи знаки корней.

Тригонометрические выражения

Для работы с такими функциями необходимо пользоваться свойствами, основными формулами прямых и обратных функций. Статья преобразование тригонометрических функций раскроет этот вопрос подробней.

Логарифмические выражения

После знакомства с логарифмами можно говорить о сложных логарифмических выражениях.

Выражения, которые имеют логарифмы, называют логарифмическими.

Для углубления изучения материала, следует обратиться к материалу о преобразовании логарифмических выражений.

Дроби

Существуют выражения особого вида, которые получили название дроби. Так как они имеют числитель и знаменатель, то они могут содержать не просто числовые значения, а также выражения любого типа. Рассмотрим определение дроби.

Дробью называют такое выражение, имеющее числитель и знаменатель, в которых имеются как числовые, так и буквенные обозначения или выражения.

Выражение общего вида

Их вид говорит о том, что можно отнести к любому из вышеперечисленных видов. Чаще всего их не относят ни к какому, так как они имеют специфичное комбинированное решение. Их рассматривают как выражения общего вида, причем для описания не используются дополнительные уточнения или выражения.

При решении такого алгебраического выражения всегда необходимо обращать внимание на его запись, наличие дроби, степеней или дополнительных выражений. Это нужно для того, чтобы точно определиться со способом его решения. Если нет уверенности в его названии, то рекомендуется называть его выражением общего типа и решать, согласно выше написанному алгоритму.

Источник

Алгебраические выражения

Всего получено оценок: 776.

Всего получено оценок: 776.

Алгебраические выражения начинают изучать в 7 классе. Они обладают рядом свойств и используются в решении задач. Изучим эту тему подробнее и рассмотрим примеры решения задачи.

Определение понятия

Какие выражения называют алгебраическими? Это математическая запись, составленная из чисел, букв и знаков арифметических действий. Наличие букв – это основное отличие числовых от алгебраических выражений. Примеры:

Буква в алгебраических выражений обозначает какое-либо число. Поэтому она называется переменной – в первом примере это буква а, во втором – b, а в третьем – с. Само алгебраическое выражение еще называют выражением с переменной.

Значение выражения

Значение алгебраического выражения – это число, получаемое в результате выполнения всех арифметических действий, которые указаны в этом выражении. Но, чтобы его получить, буквы необходимо заменить числами. Поэтому в примерах всегда указывают, какое число соответствует букве. Рассмотрим, как найти значение выражения 8а – 14 * (5 – а), если а = 3.

Подставим вместо буквы а число 3. Получаем следующую запись: 8 * 3 – 14 * (5 – 3).

Как и в числовых выражениях, решение алгебраического выражения проводится по правилам выполнения арифметических действий. Решим все по порядку.

Значение переменной называют допустимым, если при нем выражение имеет смысл, то есть возможно найти его решение.

Пример допустимой переменной для выражения 5 : (2а) – это число 1. Подставив его в выражение, получаем 5 : (2 * 1) = 2,5. Недопустимая переменная для данного выражения – это 0. Если подставить ноль в выражение, получаем 5 : (2 * 0), то есть 5 : 0. На ноль делить нельзя, значит, выражение не имеет смысла.

Тождественные выражения

Если два выражения при любых значениях, входящих в их состав переменных оказываются равны, их называют тождественными.
Пример тождественных выражений:
4 (а + с) и 4а + 4с.
Какие бы значения ни принимали буквы а и с, выражения всегда окажутся равны. Любое выражение можно заменить другим, тождественным ему. Этот процесс называют тождественным преобразованием.

Пример тождественного преобразования.
4 * (5а + 14с) – данное выражение можно заменить тождественным, применив математический закон умножения. Чтобы умножить число на сумму двух чисел, нужно это число умножить на каждое слагаемое и сложить полученные результаты.

Таким образом, выражению 4 * (5а + 14с) является тождественным 20а + 64с.

Число, стоящее в алгебраическом выражении перед буквенной переменной, называется коэффициентом. Коэффициент и переменная – это множители.

Решение задач

Алгебраические выражения используют для решения задач и уравнений.
Рассмотрим задачу. Петя придумал число. Для того, чтобы его отгадал одноклассник Саша, Петя сказал ему: сначала я прибавил к числу 7, затем вычел из него 5 и умножил на 2. В результате я получил число 28. Какое число я задумал?

Для решения задачи нужно загаданное число обозначить буквой а, а затем произвести все указанные действия с ним.

Теперь решим полученное уравнение.

Петя задумал число 12.

Что мы узнали?

Алгебраическое выражение – запись, составленная из букв, чисел и знаков арифметических действий. Каждое выражение имеет значение, которое находят путем выполнения всех арифметических действий в выражении. Буква в алгебраическом выражении называется переменной, а число перед ней – коэффициентом. Алгебраические выражения используют для решения задач.

Источник

6.4.1. Алгебраическое выражение

I. Выражения, в которых наряду с буквами могут быть использованы числа, знаки арифметических действий и скобки, называются алгебраическими выражениями.

Примеры алгебраических выражений:

Так как букву в алгебраическом выражении можно заменить какими то различными числами, то букву называют переменной, а само алгебраическое выражение — выражением с переменной.

II. Если в алгебраическом выражении буквы (переменные) заменить их значениями и выполнить указанные действия, то полученное в результате число называется значением алгебраического выражения.

Примеры. Найти значение выражения:

III. Значения буквы (переменной), при которых алгебраическое выражение имеет смысл, называют допустимыми значениями буквы (переменной).

Примеры. При каких значениях переменной выражение не имеет смысла?

Решение. Мы знаем, что на нуль делить нельзя, поэтому, каждое из данных выражений не будет иметь смысла при том значении буквы (переменной), которая обращает знаменатель дроби в нуль!

В примере 1) это значение а = 0. Действительно, если вместо а подставить 0, то нужно будет число 6 делить на 0, а этого делать нельзя. Ответ: выражение 1) не имеет смысла при а = 0.

В примере 2) знаменатель х — 4 = 0 при х = 4, следовательно, это значение х = 4 и нельзя брать. Ответ: выражение 2) не имеет смысла при х = 4.

Пример: 5 (a – b) и 5a – 5b тожественно равны, так как равенство 5 (a – b) = 5a – 5b будет верным при любых значениях a и b. Равенство 5 (a – b) = 5a – 5b есть тождество.

Тождество – это равенство, справедливое при всех допустимых значениях входящих в него переменных. Примерами уже известных вам тождеств являются, например, свойства сложения и умножения, распределительное свойство.

Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.

a) преобразуйте выражение в тождественно равное, используя распределительное свойство умножения:

Решение. Вспомним распределительное свойство (закон) умножения:

(a+b)·c=a·c+b·c (распределительный закон умножения относительно сложения: чтобы сумму двух чисел умножить на третье число, можно каждое слагаемое умножить на это число и полученные результаты сложить).
(а-b)·c=a·с-b·c (распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно умножить на это число уменьшаемое и вычитаемое отдельно и из первого результата вычесть второй).

1) 10·(1,2х + 2,3у) = 10 · 1,2х + 10 · 2,3у = 12х + 23у.

б) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное свойства (законы) сложения:

Решение. Применим законы (свойства) сложения:

a+b=b+a (переместительный: от перестановки слагаемых сумма не меняется).
(a+b)+c=a+(b+c) (сочетательный: чтобы к сумме двух слагаемых прибавить третье число, можно к первому числу прибавить сумму второго и третьего).

4) х + 4,5 +2х + 6,5 = (х + 2х) + (4,5 + 6,5) = 3х + 11.

5) (3а + 2,1) + 7,8 = 3а + (2,1 + 7,8) = 3а + 9,9.

в) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное свойства (законы) умножения:

Решение. Применим законы (свойства) умножения:

a·b=b·a (переместительный: от перестановки множителей произведение не меняется).
(a·b)·c=a·(b·c) (сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего).

Если алгебраическое выражение дано в виде сократимой дроби, то пользуясь правилом сокращения дроби его можно упростить, т.е. заменить тождественно равным ему более простым выражением.

Примеры. Упростите, используя сокращение дробей.

Решение. Сократить дробь — это значит разделить ее числитель и знаменатель на одно и то же число (выражение), отличное от нуля. Дробь 10) сократим на 3b; дробь 11) сократим на а и дробь 12) сократим на 7n. Получаем:

Алгебраические выражения применяют для составления формул.

Формула – это алгебраическое выражение, записанное в виде равенства и выражающее зависимость между двумя или несколькими переменными. Пример: известная вам формула пути s=v·t (s — пройденный путь, v — скорость, t — время). Вспомните, какие еще формулы вы знаете.

Источник