какие граничные условия называются естественными
Какие граничные условия называются естественными
Пример 7.1. Решить пример 2.1 при незаданном граничном условии на правом конце.
Общее решение имеет вид (2.16). Естественное граничное условие (7.4) по (2.12) даёт:
Составляем систему уравнений для нахождения произвольных постоянных:
Отсюда и решение задачи:
Проверим с помощью MATLAB, чему равен функционал (2.10) на кривой (7.7):
Видно, что полученное значение меньше результата примера 2.1: там Это и не удивительно: раз мы ищем минимум на более широком классе функций, то он будет по крайней мере не больше, а, может быть, и меньше, чем минимум на более узком классе функций.
К этому результату можно прийти и другим путём. Возьмём все функции вида (2.16) (общее решение уравнения Эйлера), и выберем из них те, что удовлетворяют граничному условию на левом конце. Из уравнения (2.17) имеем: и любое решение уравнения Эйлера, проходящее через точку имеет вид:
Каким же нужно взять C1, чтобы функционал (2.10) принял экстремальное значение? Решим эту задачу с помощью MATLAB:
7.2. Функционал, зависящий от нескольких функций, без граничного условия
Материал этого раздела изложен в книге.
7.3. Вопросы для самопроверки
7.4. Примеры выполнения заданий
7.4.1. Задание 1
Найти экстремаль функционала, рассмотренного ранее в примере 1 главы 2, при том же самом граничном условии на левом конце, и при незаданном граничном условии на правом конце. Сравнить решение с решением задания 1 главы 2.
Составим программу для решения этой задачи. Так как нам нужно сравнить решение с заданием 1 главы 2, воспользуемся программой для этого примера, как заготовкой. Внесём в неё такие изменения:
Теперь переходим к решению нашего примера. Аналитическое решение дифференциального уравнения Эйлера получено − оно такое же, как и для задания 2.1. Для нахождения произвольных постоянных нам нужно сформировать систему уравнений. Граничное условие слева − такое же. Формируем естественное граничное условие на правом конце. Для этого в формулу (7.4) подставляем сначала y и y‘, а затем x2 во все выражения вместо x.
Решаем систему уравнений EqLeft и EqRightNat − находим произвольные постоянные. Подставляем их в решение. Находим значение функционала на полученной экстремали.
Далее, как и в задании 2.1, заполняем таблицу и строим графики решений двух примеров на одном рисунке: красная сплошная линия − решение нашего примера, а синяя пунктирная − решение задания 2.1.
7.4.2. Задание 2
Найти экстремаль функционала (3.14), рассмотренного ранее в главе 3, при тех же самых граничных условиях на левом конце, и при незаданных граничных условиях на правом конце. Сравнить решение с решением задания из главы 3.
Программу для решения этого примера будем составлять на основе программы для задания из главы 3. Внесём в неё такие же изменения, как и в программу предыдущего задания 7.1. А именно: уберём все печати, кроме исходных данных и естественных граничных условий Fy’ и Fz’. Значение функционала вычислим только на экстремали − решении задания 3. Графики также пока не строим.
Решаем полученную систему уравнений, и подставляем значения найденных констант в и Печатаем найденные решения. Вычисляем значение функционала на экстремали.
Заполняем таблицу для построения графика. Строим на трёх отдельных графиках результаты вычислений. Вначале строим двумерные графики функций сплошной красной линией для нашего задания 7.2, а пунктирной синей − для задания из главы 3. Затем на новом рисунке строим двумерные графики функций также сплошной красной линией для нашего задания, а пунктирной синей − для задания главы 3. И, наконец, строим трёхмерный график: сплошная красная линия − решение нашего задания, а пунктирная синяя − задания главы 3. Выбираем точку просмотра. Показываем сетку и контур.


7.4.3. Задание 3
Решить задачу о брахистохроне, соединяющей точку с точкой M2, у которой задана абсцисса и не задана ордината y2. Сравнить решение полученной задачи с решением задачи при закреплённом правом конце Вычислить время прохождения дистанции лыжником с рис. 1.4 в том и другом случае. Нарисовать графики.
Теперь найдём решение нашей задачи: запрограммируем вычисления по формуле (7.14). Напечатаем найденное решение.
Вычислим значение функционала (2.74) для обоих вариантов. Решение у нас получено в параметрической форме, поэтому дифференциал длины дуги будет иметь несколько иной вид. Вспомните, как он записывается для функции, заданной параметрически. Описываем необходимые символические переменные, строим из них подынтегральную функцию. Вычисляем функционалы для обоих вариантов и печатаем их.
Какое время оказалось меньше?
Теперь рисуем обе брахистохроны на одном графике. Как обычно, синей пунктирной линией рисуем решение старого примера, а красной сплошной − нашего 7.3.
Большая Энциклопедия Нефти и Газа
Естественные граничные условия
Естественные граничные условия должны давать зависимость между составляющей тензора напряжения в направлении нормали, к площадке границы тела, которую называют вектором напряжения, действующим на площадку границы, и вектором смещения. [1]
Уравнения Эйлера и естественные граничные условия задачи на условное стационарное значение частного функционала составляют вместе с дополнительными условиями полный комплекс уравнений и граничных условий данной теории. [3]
Так как уравнения Эйлера и естественные граничные условия являются необходимыми и достаточными условиями стационарности ( гл. [4]
Наконец, отметим простой метод, который позволяет отличить естественные граничные условия от главных и который применим для ряда краевых задач. [7]
Система уравнений теории упругости и граничные условия представляют собою уравнения Эйлера и естественные граничные условия некоторой вариационной задачи. [8]
Вместо устойчивых или неустойчивых граничных условий в литературе часто встречаются термины основные или естественные граничные условия соответственно. [9]
Приравнивая нулю первые вариации функционалов Ф ], Ф2, Фз, получим дифференциальные уравнения и естественные граничные условия для отыскания собственных значений и собственных функций. [11]
Учитывая формулу ( 74), найдем, что уравнения ( 31) и соответствующие им естественные граничные условия ( 35) не отличаются от тех, которые имеют место в задаче изгиба. [12]
Силовые граничные условия учитываются уравнениями вида (6.2.8), а кинематические и смешанные граничные условия следуют из вариационного уравнения (4.2.11) как естественные граничные условия при заданных дополнительных ограничениях на виртуальные скорости узловых точек. [13]
Естественные граничные условия
Краткие теоретические сведения
Рассмотрим задачу вариационного исчисления для функционала (1.1), зависящего от функции одной переменной и её производной. Но, в отличие от (1.2), пусть задано граничное условие только на левом конце: y(x1)y1. На правом конце x2 значение функции может быть произвольным, то есть экстремум функционала (1.1) ищется на классе функций с закреплённым левым концом и свободным правым. Этот класс является более широким, чем рассмотренный в главе 1 класс функций с двумя закреплёнными концами.
Необходимым условием экстремума функционала является равенство нулю его вариации: J0. Так как функционал J(y) достигает экстремума на классе функций с произвольным значением y(x2), то он тем более будет достигать экстремума на более узком классе функций: с неподвижной правой точкой. Следовательно, экстремаль должна удовлетворять дифференциальному уравнению Эйлера (1.5). Это уравнение дополняется граничным условием на левом конце: y(x1)y1. Недостающее второе граничное условие находим из необходимого условия экстремума: J0. Вычислим вариацию функционала и приравняем её нулю. Разложим подынтегральную функцию F в ряд Тейлора в окрестности экстремали, и удержим в этом разложении только линейные члены. Проинтегрируем полученное выражение по частям и воспользуемся тем, что экстремаль удовлетворяет уравнению Эйлера.
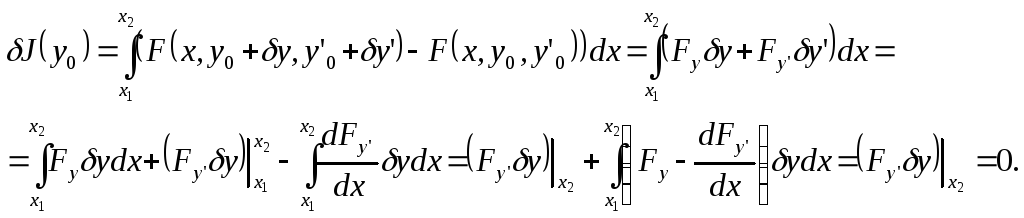
В силу произвольности y(x2) получаем второе граничное условие:
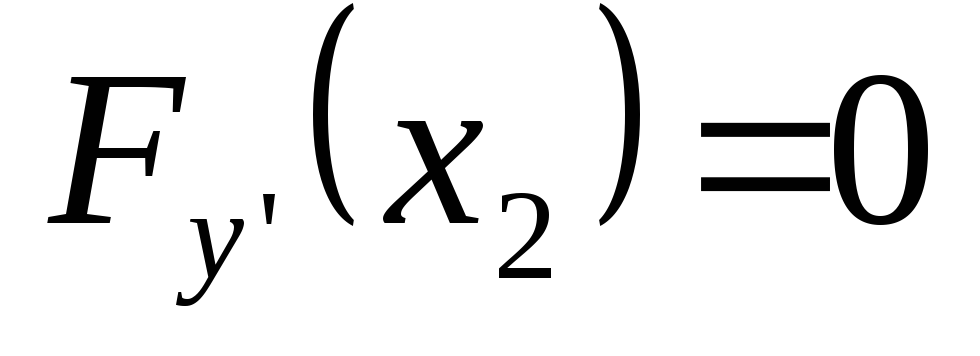
Это граничное условие называется естественным. Его смысл следующий: если из всех экстремалей, удовлетворяющих заданному граничному условию слева и различным граничным условиям справа, выбрать функцию, доставляющую экстремум функционалу, то эта функция будет удовлетворять естественному граничному условию на правом конце (5.2).
Аналогично решается задача для функционала вида (2.1), зависящего от нескольких функций, если граничные условия заданы только на одном из концов (например, на левом). В этом случае недостающие граничные условия на правом конце имеют вид
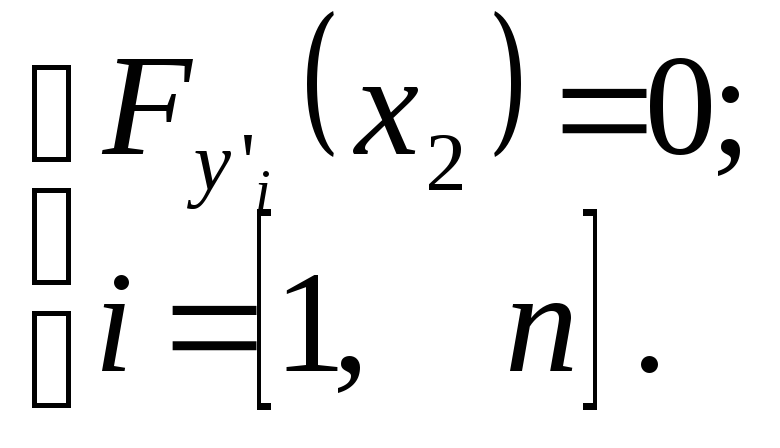
Задача для самостоятельного решения. Выведите естественное граничное условие для функционала (3.1), зависящего от функции и её производных до 2-го порядка включительно, если граничные условия (3.2) заданы только на левом конце интервала x1, а на правом конце x2 заданы или только значение функции (вариант 1), или только значение производной (вариант 2), или ничего не задано (вариант 3).
Примеры выполнения заданий
Пример 5a
Найти экстремаль функционала (1.6), рассмотренного ранее в примере 1a, при том же самом граничном условии на левом конце, и при незаданном граничном условии на правом конце. Сравнить решение с решением задачи 1a.
Составим программу для решения этой задачи. Так как нам нужно сравнить решение с 1a, поэтому воспользуемся программой для примера 1a, как заготовкой. Оставим полностью решение примера 1a, вплоть до заполнения таблицы, но уберём печать результатов и рисование графика. Оставим только печать левой части естественного граничного условия (5.1) Fy.
disp(‘Решаем пример 5a’)
x1=-1; % вводим граничные условия
Тест по теме 4.1 «Моделирование систем»
1. Что такое модель объекта?
A. Объект-заместитель объекта-оригинала, обеспечивающий изучение всех свойств оригинала
B. Объект-оригинал, который обеспечивает изучение некоторых своих свойств
C. Объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала
D. Объект-оригинал, который обеспечивает изучение всех своих свойств
2. Какие граничные условия называются естественными?
A. Условия, налагаемые на функцию, которая ищется.
B. Условия, которые накладываются на производные функции, ищется, по пространственным координатам.
C. Условия, наложено на различные внешние силовые факторы, действующие на точки поверхности тела.
D. Условия, наложено на различные внутренние факторы, которые действуют внутри тела.
3. Какому вариационной принципа соответствует формулировка МКЭ в перемещениях?
A. Минимума дополнительной работы Кастильяно.
B. Минимума потенциальной энергии Лагранжа.
C. Принцип Хувашицу.
D. Максимум потенциальной работы Кастильяно.
4. Какой тип математических моделей использует алгоритмы?
5. Какой тип моделей выделен в классификации по принципам построения.
6. Какие зависимые переменные существуют в моделях микроуровня?
B. Пространственные координаты.
C. Плотность и масса.
D. Фазовые координаты.
7. Какой метод дискретизации модели относится к микроуровня?
A. Метод свободных сетей.
B. Метод конечных разностей.
C. Метод узловых давлений.
8. Что такое уровне проектирования?
A. Временное распределения работ по созданию новых объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, которая определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
9. Что называют краевыми условиями для системы уравнений математической модели?
A. Условия, накладываемые на границе исследуемой области и в начальный момент времени.
B. Условия, налагаемые на функцию, ищут.
C. Условия, налагаемые на производные искомой функции.
D. Условия, накладываемые в начальный момент времени.
10. Что такое аспекты проектирования?
A. Временное распределение работ по созданию объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с где-либо определяемой точки зрения, определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
11. Укажите, какой из этапов выполняется при математическом моделировании после анализа.
A. Создание объекта, процесса или системы.
B. Проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента.
C. Корректировка постановки задачи после проверки адекватности модели.
D. Использование модели.
12. Что такое параметры системы?
A. Величины, которая выражают свойство или системы, или ее части, или окружающей среды.
B. Величины, характеризующие энергетическое или информационное наполнение элемента или подсистемы.
C. Свойства элементов объекта.
D. Величины, которая характеризует действия, которые могут выполнять объекты.
13. Какие формулировки МКЭ существуют в зависимости от функции, ищут?
A. В перемещениях и деформациях
C. В напряжениях и градиентах.
D. Смешанная и гибридная.
14. Какие зависимые переменные существуют в моделях макроуровня?
A. Время и характеристики потока.
B. Фазовые переменные типа потенциала.
C. Пространственные координаты.
D. Фазовые переменные типа потока.
15. Что такое проектирование?
A. Процесс, который заключается в получении и преобразовании исходного описания объекта в конечный описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера.
B. Процесс создания в заданных условиях описания несуществующего объекта на базе первичной описания.
C. Первоначальный описание объекта проектирования.
D. Вторичный описание объекта.
Вариант 2
1. Что такое уровне проектирования?
A. Временное распределения работ по созданию новых объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, которая определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
2. Что называют краевыми условиями для системы уравнений математической модели?
A. Условия, накладываемые на границе исследуемой области и в начальный момент времени.
B. Условия, налагаемые на функцию, ищут.
C. Условия, налагаемые на производные искомой функции.
D. Условия, накладываемые в начальный момент времени.
3. Что такое аспекты проектирования?
A. Временное распределение работ по созданию объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с где-либо определяемой точки зрения, определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
4. Укажите, какой из этапов выполняется при математическом моделировании после анализа.
A. Создание объекта, процесса или системы.
B. Проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента.
C. Корректировка постановки задачи после проверки адекватности модели.
D. Использование модели.
5. Что такое параметры системы?
A. Величины, которая выражают свойство или системы, или ее части, или окружающей среды.
B. Величины, характеризующие энергетическое или информационное наполнение элемента или подсистемы.
C. Свойства элементов объекта.
D. Величины, которая характеризует действия, которые могут выполнять объекты.
6. Какие формулировки МКЭ существуют в зависимости от функции, ищут?
A. В перемещениях и деформациях
C. В напряжениях и градиентах.
D. Смешанная и гибридная.
7. Какие зависимые переменные существуют в моделях макроуровня?
A. Время и характеристики потока.
B. Фазовые переменные типа потенциала.
C. Пространственные координаты.
D. Фазовые переменные типа потока.
8. Что такое проектирование?
A. Процесс, который заключается в получении и преобразовании исходного описания объекта в конечный описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера.
B. Процесс создания в заданных условиях описания несуществующего объекта на базе первичной описания.
C. Первоначальный описание объекта проектирования.
D. Вторичный описание объекта.
9. Что такое модель объекта?
A. Объект-заместитель объекта-оригинала, обеспечивающий изучение всех свойств оригинала
B. Объект-оригинал, который обеспечивает изучение некоторых своих свойств
C. Объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала
D. Объект-оригинал, который обеспечивает изучение всех своих свойств
10. Какие граничные условия называются естественными?
A. Условия, налагаемые на функцию, которая ищется.
B. Условия, которые накладываются на производные функции, ищется, по пространственным координатам.
C. Условия, наложено на различные внешние силовые факторы, действующие на точки поверхности тела.
D. Условия, наложено на различные внутренние факторы, которые действуют внутри тела.
11. Какому вариационной принципа соответствует формулировка МКЭ в перемещениях?
A. Минимума дополнительной работы Кастильяно.
B. Минимума потенциальной энергии Лагранжа.
C. Принцип Хувашицу.
D. Максимум потенциальной работы Кастильяно.
12. Какой тип математических моделей использует алгоритмы?
13. Какой тип моделей выделен в классификации по принципам построения.
14. Какие зависимые переменные существуют в моделях микроуровня?
B. Пространственные координаты.
C. Плотность и масса.
D. Фазовые координаты.
15. Какой метод дискретизации модели относится к микроуровня?
A. Метод свободных сетей.
B. Метод конечных разностей.
C. Метод узловых давлений.
Вариант 3
1. Какие зависимые переменные существуют в моделях микроуровня?
B. Пространственные координаты.
C. Плотность и масса.
D. Фазовые координаты.
2. Какой метод дискретизации модели относится к микроуровня?
A. Метод свободных сетей.
B. Метод конечных разностей.
C. Метод узловых давлений.
3. Что такое уровне проектирования?
A. Временное распределения работ по созданию новых объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, которая определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
4. Что называют краевыми условиями для системы уравнений математической модели?
A. Условия, накладываемые на границе исследуемой области и в начальный момент времени.
B. Условия, налагаемые на функцию, ищут.
C. Условия, налагаемые на производные искомой функции.
D. Условия, накладываемые в начальный момент времени.
5. Что такое аспекты проектирования?
A. Временное распределение работ по созданию объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с где-либо определяемой точки зрения, определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
6. Что такое модель объекта?
A. Объект-заместитель объекта-оригинала, обеспечивающий изучение всех свойств оригинала
B. Объект-оригинал, который обеспечивает изучение некоторых своих свойств
C. Объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала
D. Объект-оригинал, который обеспечивает изучение всех своих свойств
7. Какие граничные условия называются естественными?
A. Условия, налагаемые на функцию, которая ищется.
B. Условия, которые накладываются на производные функции, ищется, по пространственным координатам.
C. Условия, наложено на различные внешние силовые факторы, действующие на точки поверхности тела.
D. Условия, наложено на различные внутренние факторы, которые действуют внутри тела.
8. Какому вариационной принципа соответствует формулировка МКЭ в перемещениях?
A. Минимума дополнительной работы Кастильяно.
B. Минимума потенциальной энергии Лагранжа.
C. Принцип Хувашицу.
D. Максимум потенциальной работы Кастильяно.
9. Какой тип математических моделей использует алгоритмы?
10. Какой тип моделей выделен в классификации по принципам построения.
11. Укажите, какой из этапов выполняется при математическом моделировании после анализа.
A. Создание объекта, процесса или системы.
B. Проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента.
C. Корректировка постановки задачи после проверки адекватности модели.
D. Использование модели.
12. Что такое параметры системы?
A. Величины, которая выражают свойство или системы, или ее части, или окружающей среды.
B. Величины, характеризующие энергетическое или информационное наполнение элемента или подсистемы.
C. Свойства элементов объекта.
D. Величины, которая характеризует действия, которые могут выполнять объекты.
13. Какие формулировки МКЭ существуют в зависимости от функции, ищут?
A. В перемещениях и деформациях
C. В напряжениях и градиентах.
D. Смешанная и гибридная.
14. Какие зависимые переменные существуют в моделях макроуровня?
A. Время и характеристики потока.
B. Фазовые переменные типа потенциала.
C. Пространственные координаты.
D. Фазовые переменные типа потока.
15. Что такое проектирование?
A. Процесс, который заключается в получении и преобразовании исходного описания объекта в конечный описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера.
B. Процесс создания в заданных условиях описания несуществующего объекта на базе первичной описания.
C. Первоначальный описание объекта проектирования.
D. Вторичный описание объекта.
1. Укажите, какой из этапов выполняется при математическом моделировании после анализа.
A. Создание объекта, процесса или системы.
B. Проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента.
C. Корректировка постановки задачи после проверки адекватности модели.
D. Использование модели.
2. Что такое параметры системы?
A. Величины, которая выражают свойство или системы, или ее части, или окружающей среды.
B. Величины, характеризующие энергетическое или информационное наполнение элемента или подсистемы.
C. Свойства элементов объекта.
D. Величины, которая характеризует действия, которые могут выполнять объекты.
3. Какие формулировки МКЭ существуют в зависимости от функции, ищут?
A. В перемещениях и деформациях
C. В напряжениях и градиентах.
D. Смешанная и гибридная.
4. Какие зависимые переменные существуют в моделях макроуровня?
A. Время и характеристики потока.
B. Фазовые переменные типа потенциала.
C. Пространственные координаты.
D. Фазовые переменные типа потока.
5. Что такое проектирование?
A. Процесс, который заключается в получении и преобразовании исходного описания объекта в конечный описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера.
B. Процесс создания в заданных условиях описания несуществующего объекта на базе первичной описания.
C. Первоначальный описание объекта проектирования.
D. Вторичный описание объекта.
6. Что такое модель объекта?
A. Объект-заместитель объекта-оригинала, обеспечивающий изучение всех свойств оригинала
B. Объект-оригинал, который обеспечивает изучение некоторых своих свойств
C. Объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала
D. Объект-оригинал, который обеспечивает изучение всех своих свойств
7. Какие граничные условия называются естественными?
A. Условия, налагаемые на функцию, которая ищется.
B. Условия, которые накладываются на производные функции, ищется, по пространственным координатам.
C. Условия, наложено на различные внешние силовые факторы, действующие на точки поверхности тела.
D. Условия, наложено на различные внутренние факторы, которые действуют внутри тела.
8. Какому вариационной принципа соответствует формулировка МКЭ в перемещениях?
A. Минимума дополнительной работы Кастильяно.
B. Минимума потенциальной энергии Лагранжа.
C. Принцип Хувашицу.
D. Максимум потенциальной работы Кастильяно.
9. Какой тип математических моделей использует алгоритмы?
10. Какой тип моделей выделен в классификации по принципам построения.
11. Какие зависимые переменные существуют в моделях микроуровня?
B. Пространственные координаты.
C. Плотность и масса.
D. Фазовые координаты.
12. Какой метод дискретизации модели относится к микроуровня?
A. Метод свободных сетей.
B. Метод конечных разностей.
C. Метод узловых давлений.
13. Что такое уровне проектирования?
A. Временное распределения работ по созданию новых объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, которая определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
14. Что называют краевыми условиями для системы уравнений математической модели?
A. Условия, накладываемые на границе исследуемой области и в начальный момент времени.
B. Условия, налагаемые на функцию, ищут.
C. Условия, налагаемые на производные искомой функции.
D. Условия, накладываемые в начальный момент времени.
10. Что такое аспекты проектирования?
A. Временное распределение работ по созданию объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с где-либо определяемой точки зрения, определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |
| 1 | C | B | D | C |
| 2 | B | A | B | A |
| 3 | B | D | B | D |
| 4 | C | C | A | C |
| 5 | B | A | D | A |
| 6 | D | D | C | C |
| 7 | B | C | B | B |
| 8 | B | A | B | B |
| 9 | A | C | C | C |
| 10 | D | B | B | B |
| 11 | C | B | C | D |
| 12 | A | C | A | B |
| 13 | D | B | D | B |
| 14 | C | D | C | A |
| 15 | A | B | A | D |
Критерий оценки:
— оценка «5» выставляется студенту, если студент набрал баллы: от 13 до 15;
— оценка «4» выставляется студенту, если студент набрал баллы: от 10 до 12;
— оценка «3» выставляется студенту, если студент набрал баллы: от 7 до 9;
— оценка «2» выставляется студенту, если студент набрал баллы ниже 7.
Дата добавления: 2019-02-12 ; просмотров: 1872 ; Мы поможем в написании вашей работы!

