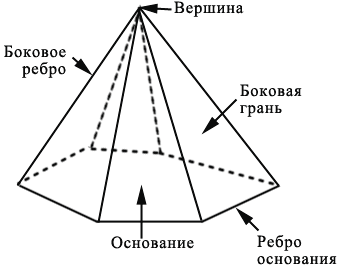
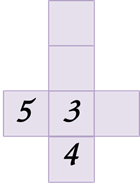
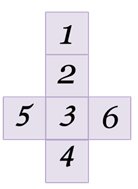
какие грани называют противолежащими

Прямоугольный параллелепипед. Пирамида.

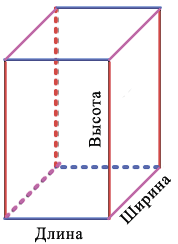
Измерения имеют названия: длина, ширина, высота. Данные названия введены, чтобы различать измерения:

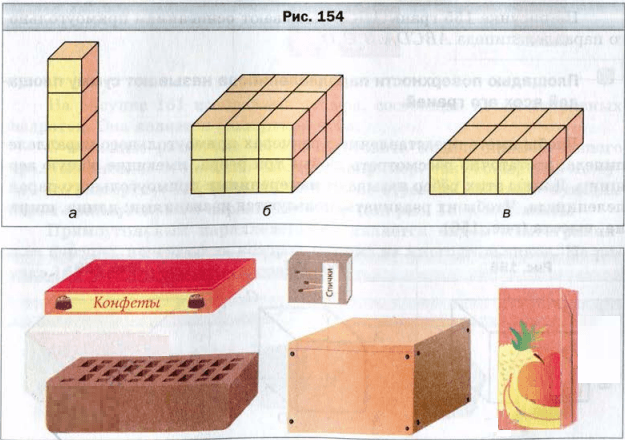
Частным случаем прямоугольного параллелепипеда является куб. Куб — это прямоугольный параллелепипед, все измерения которого равны:

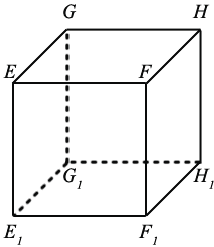
EFHGE₁F₁H₁G₁ — куб, его высота, ширина и длина равны. Гранями куба являются 6 равных квадратов.

Рассмотрим следующую фигуру:

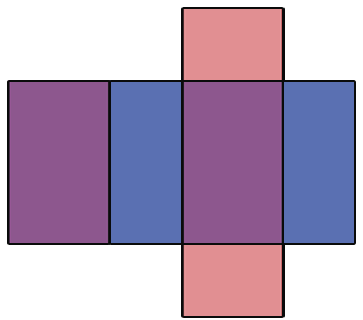
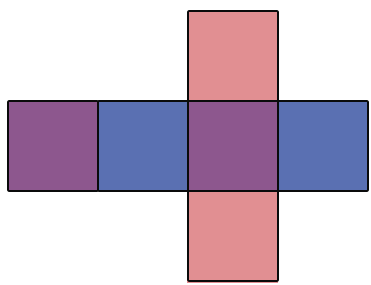
Данная фигура состоит из шести прямоугольников, которые попарно равны (выделены одним цветом). Если мы согнём по линиям данную фигуру и склеим, то получим модель прямоугольного параллелепипеда, противоположные грани которого будут одного цвета. Рассматриваемую фигуру называют развёрткой прямоугольного параллелепипеда. Как сказано выше, куб состоит из 6 равных квадратов, значит, его развертка будет иметь следующий вид:

В данном случае куб «разрезали» по 6 горизонтальным ребрам и 1 вертикальному, при этом противоположные грани выделены одним цветом. Таким образом, «разрезая» любой многогранник по ребрам так, чтобы все грани оказались в одной плоскости, можно получить его развертку. Развертки многогранников нужны, например, для создания их объемных моделей.

Если мы «разрежем» по боковым рёбрам пятиугольную пирамиду, то получим следующий многоугольник, который будет являться развёрткой данной пирамиды:

Поделись с друзьями в социальных сетях:

Источник

Прямоугольный параллелепипед. Пирамида

Прямоугольный параллелепипед ограничен шестью гранями. Каждая грань − это прямоугольник, т.е. поверхность прямоугольного параллелепипеда состоит из шести прямоугольников.

У прямоугольного параллелепипеда 8 вершин и 12 ребер.

Противолежащие грани прямоугольного параллелепипеда равны.

Площадью поверхности параллелепипеда называют сумму площадей всех его граней.

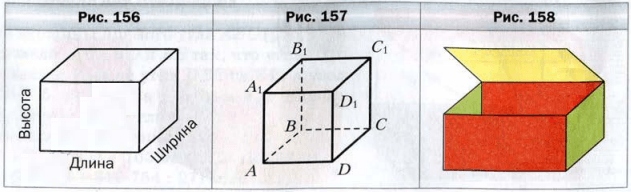
Чтобы иметь представление о размерах прямоугольного параллелепипеда, достаточно рассмотреть любые три ребра, имеющие общую вершину. Длины этих ребер называют измерениями прямоугольного параллелепипеда. Чтобы их различать, пользуются названиями: длина, ширина, высота (рис. 156 ).

Прямоугольный параллелепипед, у которого все измерения равны, называют кубом (рис. 157 ). Поверхность куба состоит из шести равных квадратов.

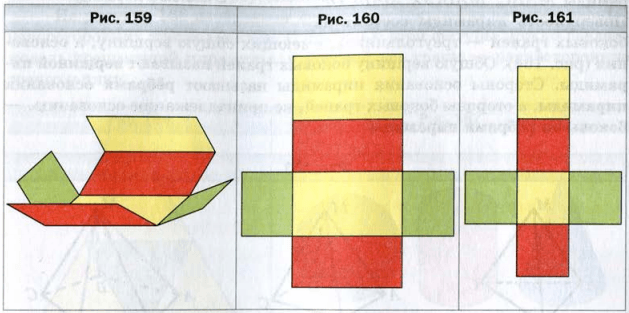
Если коробку, имеющую форму прямоугольного параллелепипеда, открыть (рис. 158 ) и разрезать по четырем вертикальным ребрам (рис. 159 ), а затем развернуть, то получим фигуру, состоящую из шести прямоугольников (рис. 160 ). Эту фигуру называют разверткой прямоугольного параллелепипеда.

На рисунке 161 изображена фигура, состоящая из шести равных квадратов. Она является разверткой куба.

С помощью развертки можно изготовить модель прямоугольного параллелепипеда.

Это можно сделать, например, так. Начертить на бумаге его развертку. Вырезать ее, согнуть по отрезкам, соответствующим ребрам прямоугольного параллелепипеда (см. рис. 159 ), и склеить.

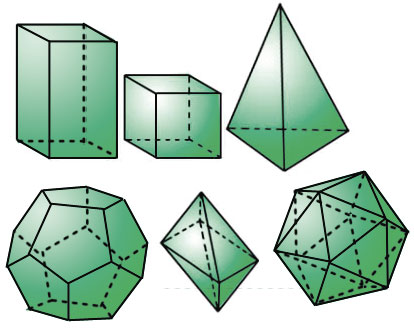
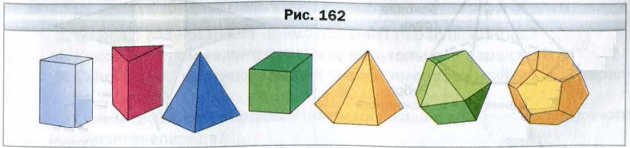
Прямоугольный параллелепипед является видом многогранника − фигуры, поверхность которой состоит из многоугольников. На рисунке 162 изображены многогранники.

Одним из видов многогранника является пирамида.

Эта фигура для вас не нова. Изучая курс Древнего мира, вы познакомились с одним из семи чудес света − египетскими пирамидами.

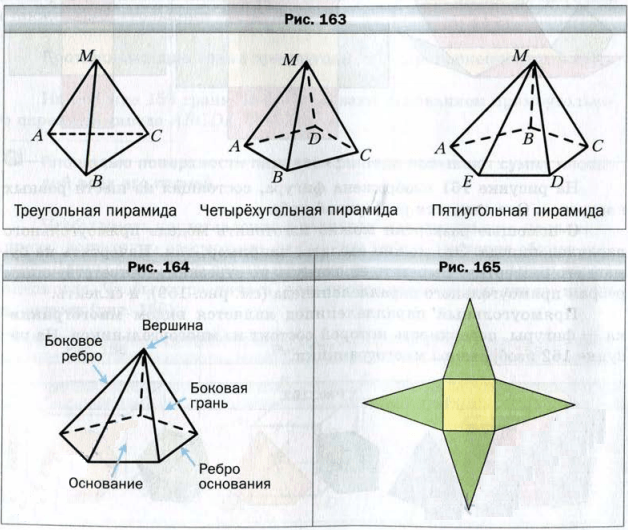
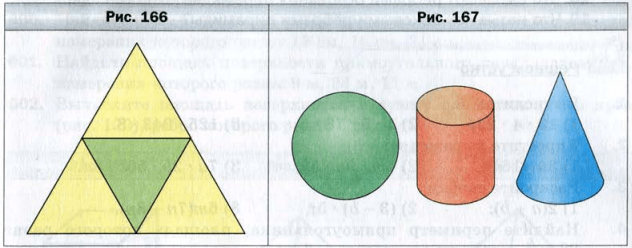
На рисунке 163 изображены пирамиды MABC, MABCD, MABCDE. Поверхность пирамиды состоит из боковых граней − треугольников, имеющих общую вершину, и основания (рис. 164 ). Общую вершину боковых граней называют ребрами основания пирамиды, а стороны боковых граней, не принадлежащие основанию, − боковыми ребрами пирамиды.

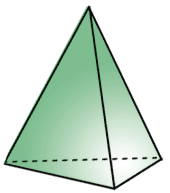
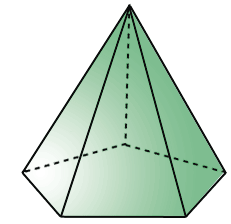
Пирамиды можно классифицировать по количеству сторон основания: треугольная, четырехугольная, пятиугольная (см. рис. 163 ) и т.д.

Поверхность треугольной пирамиды состоит из четырех треугольников. Любой из этих треугольников может служить основанием пирамиды. Это основание вид пирамиды, любая грань которой может служить ее основанием.

На рисунке 165 изображена фигура, которая может служить разверткой четырехугольной пирамиды. Она состоит из квадрата и четырех равных равнобедренных треугольников.

На рисунке 166 изображена фигура, состоящая из четырех равных равносторонних треугольников. С помощью этой фигуры можно сделать модель треугольной пирамиды, у которой все грани − равносторонние треугольники.

Многогранники являются примерами геометрических тел.

На рисунке 167 изображены знакомые вам геометрические тела, не являющиеся многогранниками. Более подробно с этими телами вы познакомитесь в 6 классе.

Источник

Геометрические фигуры. Параллелепипед.

Параллелепипед — призма, основанием которой является параллелограмм либо (равносильно) многогранник с шестью гранями, являющимися параллелограммами. Шестигранник.

Параллелограммы, из которых состоит параллелепипед являются гранями этого параллелепипеда, стороны этих параллелограммов являются ребрами параллелепипеда, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда каждая грань является параллелограммом.

Как правило выделяют любые 2-е противолежащие грани и называют их основаниями параллелепипеда, а оставшиеся грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям являются боковыми ребрами.

2 грани параллелепипеда, которые имеют общее ребро являются смежными, а те, которые не имеют общих ребер — противоположными.

Отрезок, который соединяет 2 вершины, которые не принадлежат 1-ой грани является диагональю параллелепипеда.

Длины ребер прямоугольного параллелепипеда, которые не параллельны, являются линейными размерами (измерениями) параллелепипеда. У прямоугольного параллелепипеда 3 линейных размера.

Типы параллелепипеда.

Существует несколько видов параллелепипедов:

Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.

Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов.

Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты.

Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.

Свойства параллелепипеда.

В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.

Источник

Прямоугольный параллелепипед. Что это такое?

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

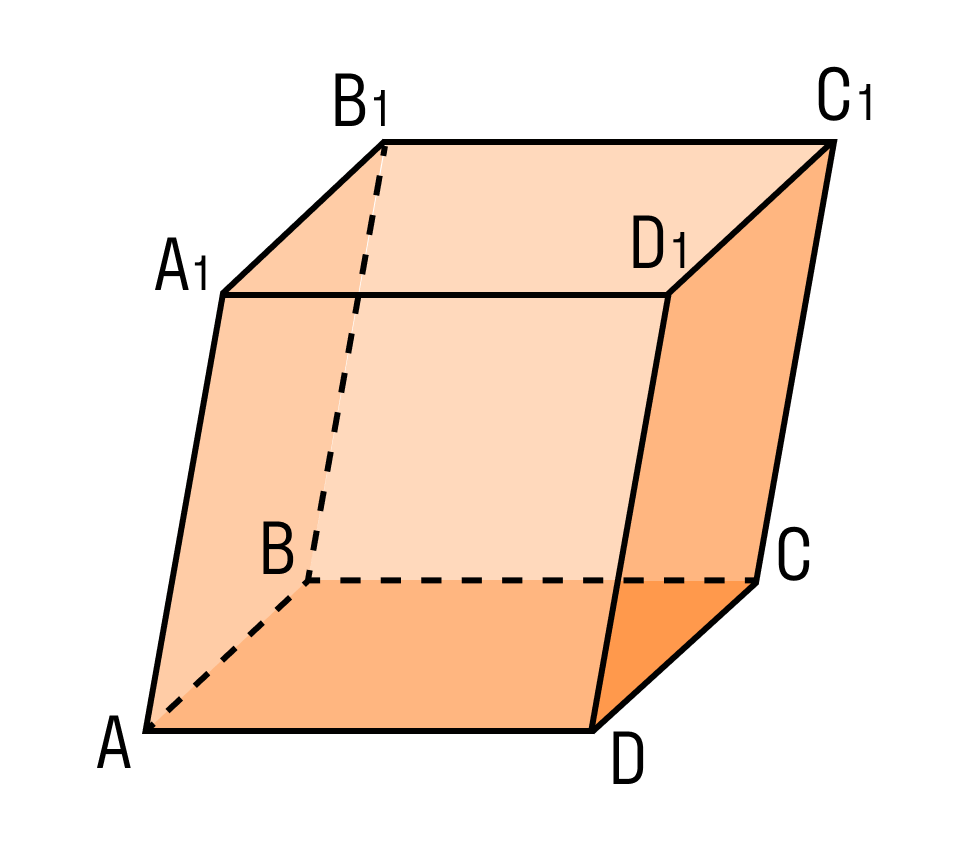
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

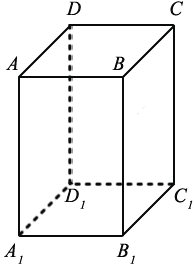
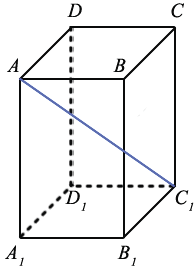
На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

Формулы прямоугольного параллелепипеда:

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

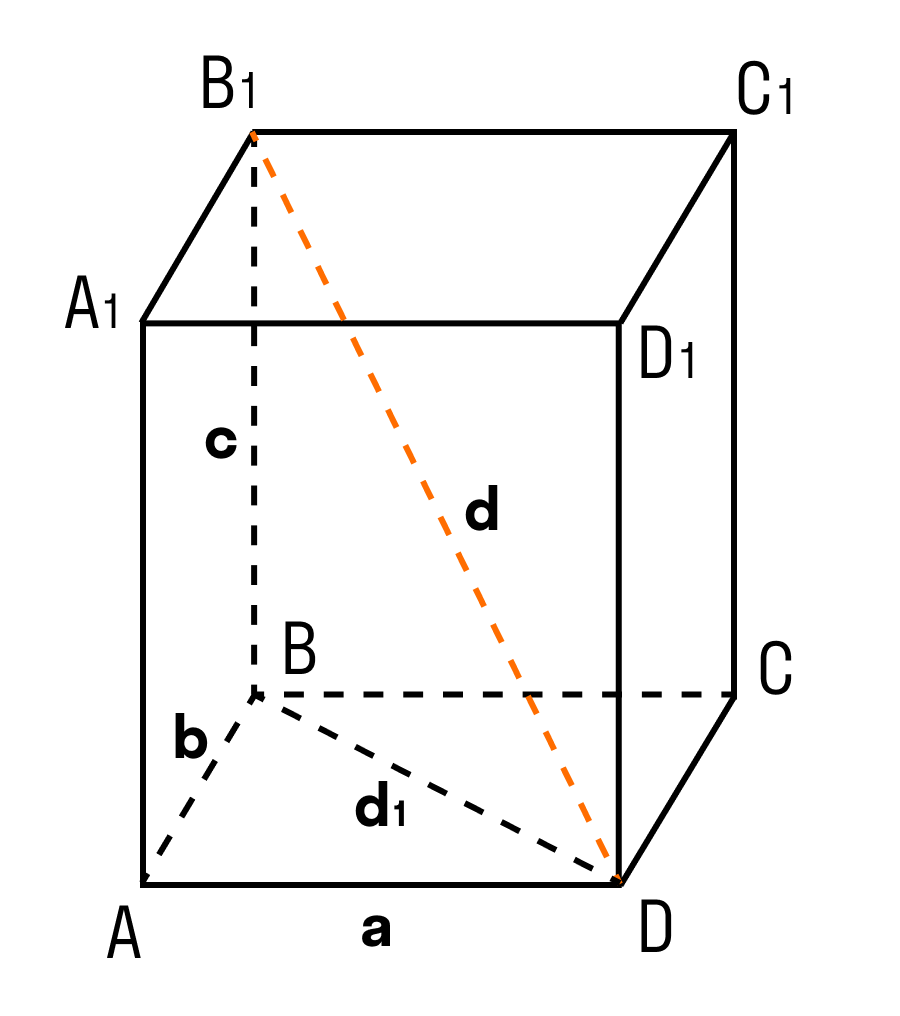
Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

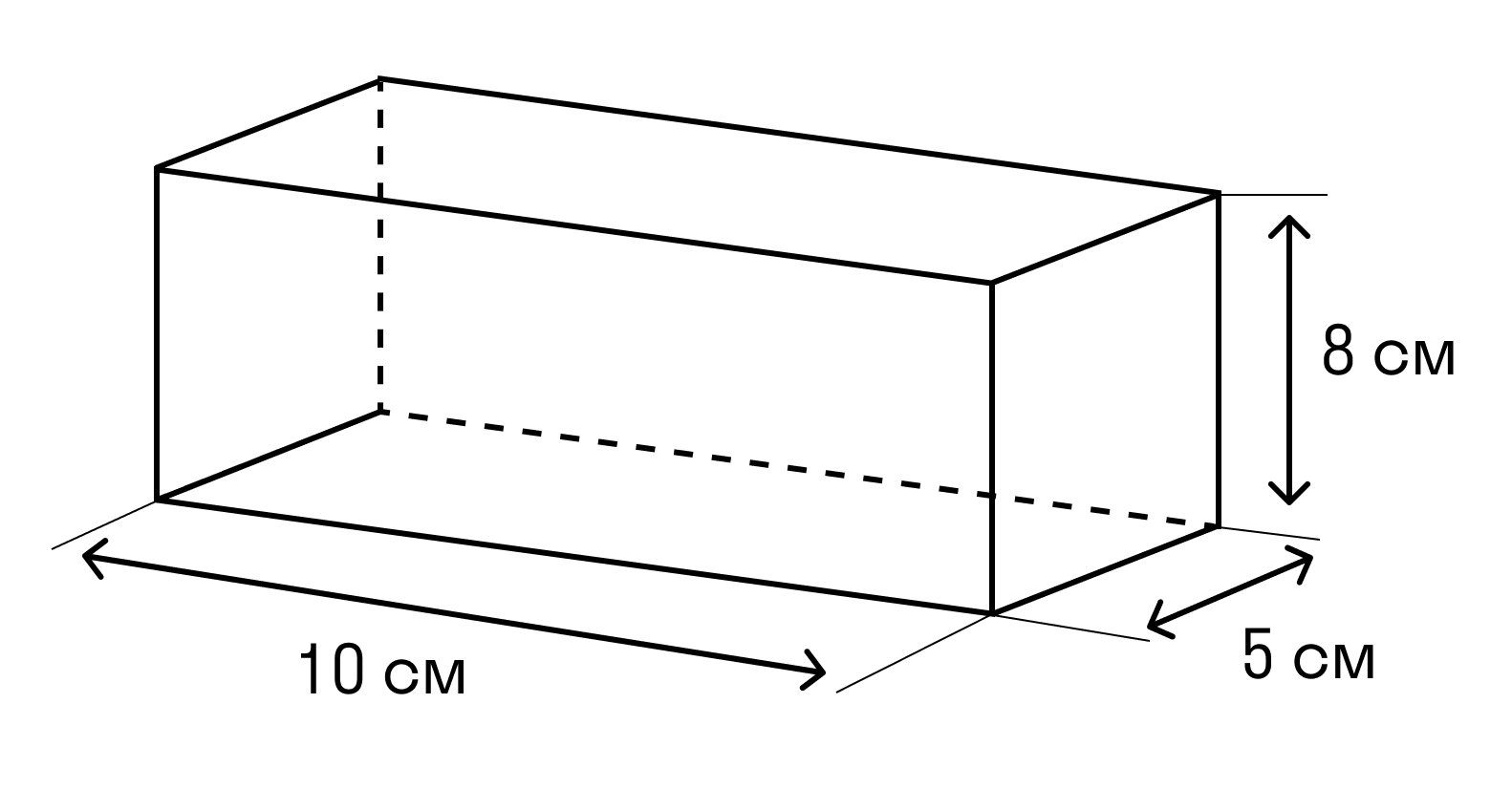
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

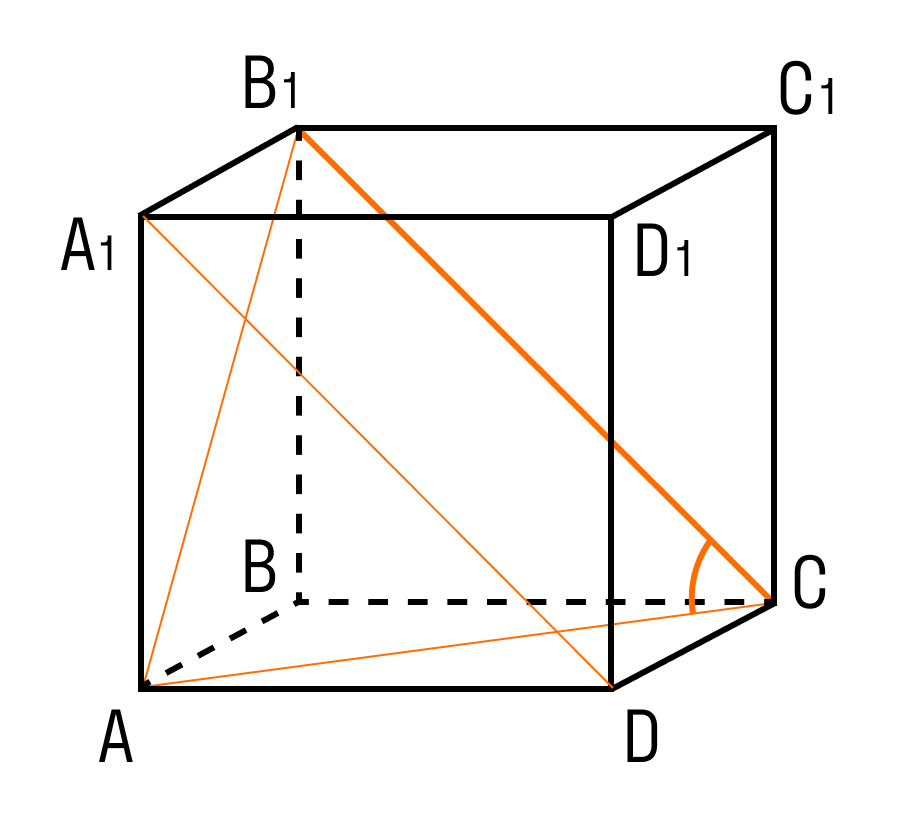
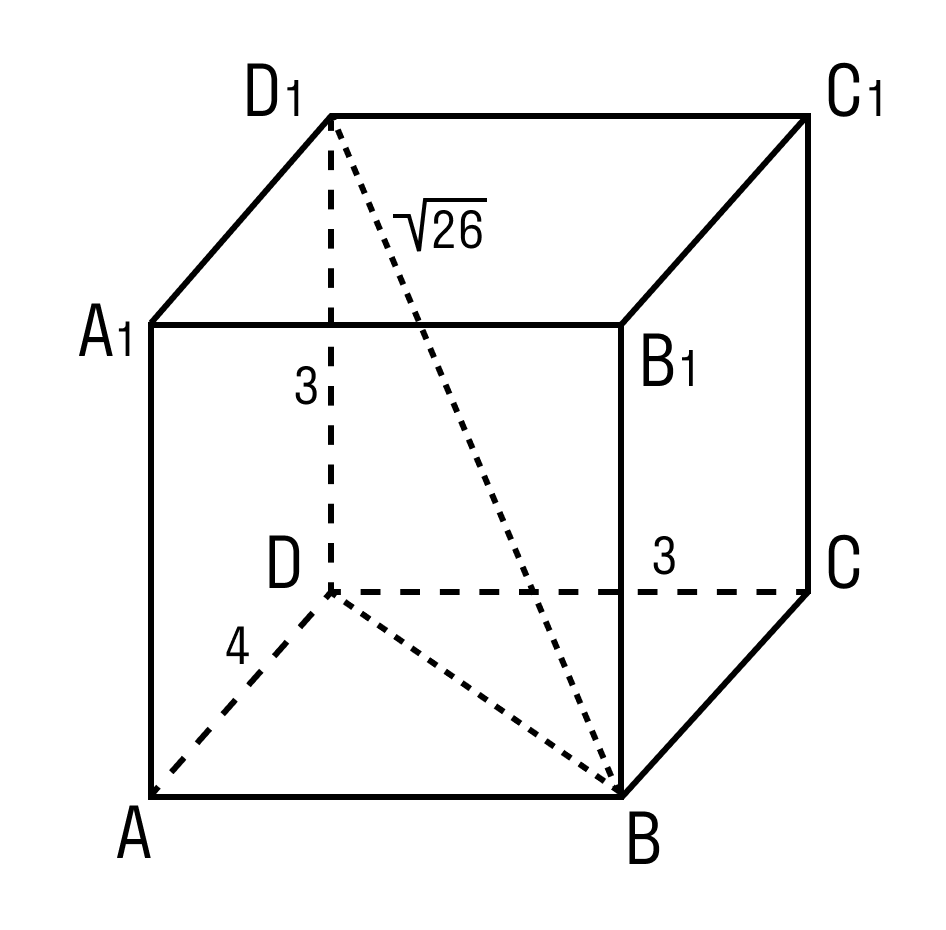
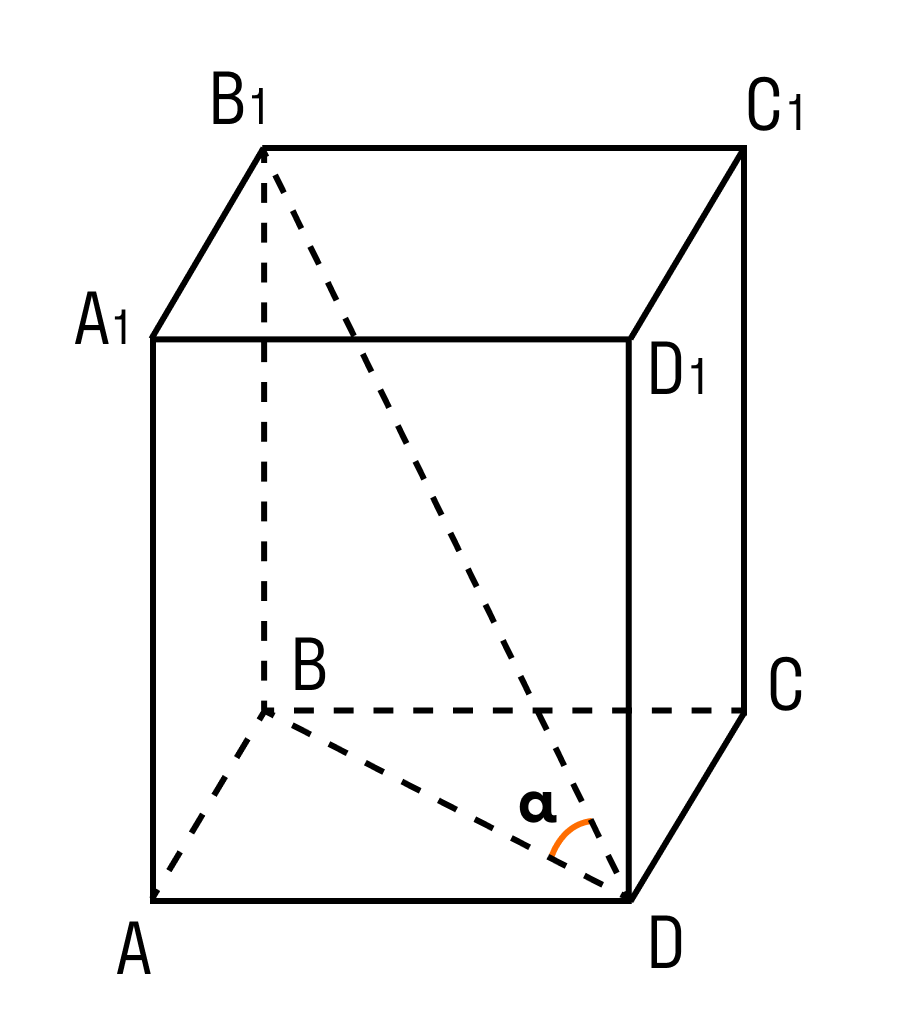
Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.

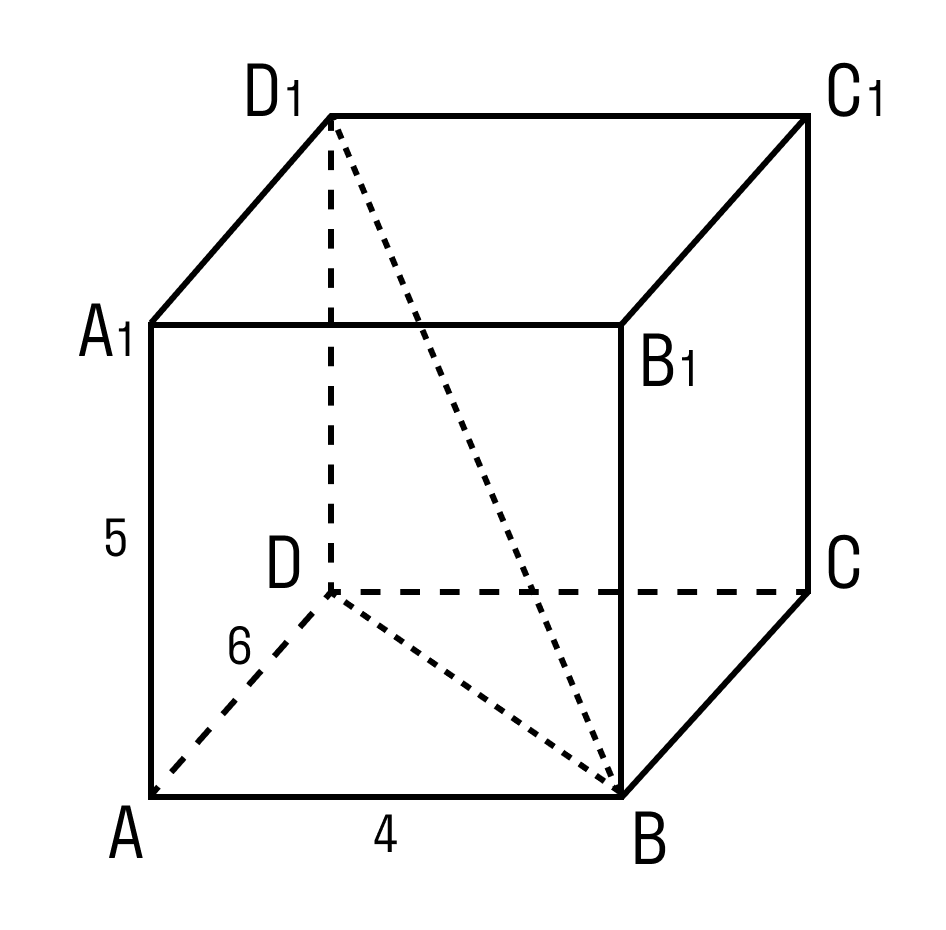
Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Прямоугольный параллелепипед. Пирамида

Урок 22. Математика 5 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Прямоугольный параллелепипед. Пирамида»

Тема урока «Прямоугольный параллелепипед. Пирамида»

Представим себе такую историю…

– Да разве бывают такие длиннющие слова? – возмущался Саша.

– Что случилось? – поинтересовался Паша.

– Нам задали разгадать математический кроссворд, – сказал Саша. — А я застрял на одном слове.

– Что за слово ты не можешь разгадать? – решил уточнить Паша.

– Представляешь, это какое-то геометрическое тело, название которого состоит из четырнадцати 14 букв, – продолжал возмущаться Саша. — А ещё в этом слове есть три буквы ЭЛ и три буквы ПЭ. Да разве бывают такие слова?

– Мне кажется, я догадался! – сказал Паша. — Попробуй записать в кроссворд слово «параллелепипед».

– Как ты сказал? – решил переспросить Саша. – Па-ла-лле-ле…, па-ра-ре-ре…, па-ла-ре-ле… Да что за мудрёное слово-то такое? Язык поломаешь, пока выговоришь!

– И совсем это слово не мудрёное, – улыбнулся Паша, – а интересное. С предметами, имеющими форму параллелепипеда, ты встречаешься каждый день.

– Не встречал я такие предметы, – сказал Саша. — А если бы встречал, то уж точно бы знал это слово.

– Встречал, встречал – продолжил Паша. — Форму прямоугольного параллелепипеда можно разглядеть в зданиях на улице. Чемодан, шкаф, комод, коробка конфет, спичечный коробок, упаковочная коробка, пакет сока, микроволновка, холодильник, системный блок компьютера тоже имеют форму параллелепипеда. И даже сейчас мы с тобой находимся внутри параллелепипеда. Ведь комната – это тоже пример прямоугольного параллелепипеда.

– Но в кроссворде же было написано, что это название геометрического тела, – перебил Саша, – а ты мне тут предметы всякие перечисляешь. Они же не геометрические тела.

– Если ты внимательно посмотришь на все эти предметы, – продолжил Паша, – и не будешь обращать внимания на их цвет, материал, из которого они сделаны, их назначение и разные мелочи, то заметишь, что все они похожи своей формой. Все эти предметы напоминают геометрическое тело – прямоугольный параллелепипед.

– Забавно! – задумался Саша. — Они и впрямь похожи формой. А расскажи мне про этот па-ра-лле-ле-пи-пед поподробнее.

– Ты знаешь, лучше обратиться к Электроше, – предложил Паша, – я думаю, он больше сможет рассказать.

– Ребята, прежде чем я вам расскажу о прямоугольном параллелепипеде, давайте немного разомнёмся и выполним устные задания, – предложил Электроша. (пауза)

– Давайте сверимся! Посмотрите, что у вас должно было получиться! (пауза)

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. — Итак, прямоугольный параллелепипед – это такая объёмная фигура, а точнее, это геометрическое тело, которое состоит из шести 6 прямоугольников.

– Электроша, ты сказал «прямоугольный» параллелепипед, – решил уточнить Саша. – А что, бывают ещё и другие параллелепипеды?

– Да, бывают и непрямоугольные параллелепипеды, – ответил Электроша, – но мы с ними познакомимся в старших классах. А сейчас мы поговорим о прямоугольном параллелепипеде.

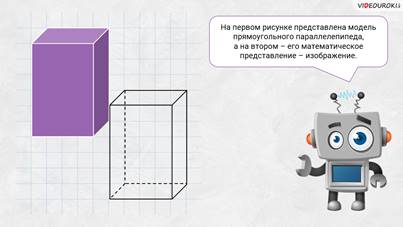
– Посмотрите на экран. На рисунках изображены два прямоугольных параллелепипеда. Правда, на первом рисунке представлена модель прямоугольного параллелепипеда, а на втором – его математическое представление – изображение.

– Электроша, а у прямоугольного параллелепипеда тоже есть свои элементы, как и у других геометрических фигур? – спросил Паша.

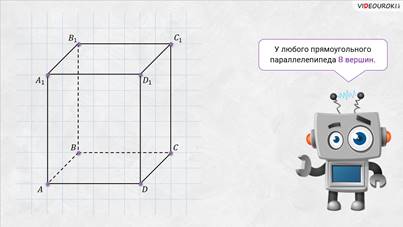
– Конечно! – сказал Электроша. — Давайте рассмотрим прямоугольный параллелепипед 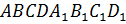А Бэ Цэ Дэ А один Бэ один Цэ один Дэ один.

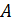
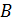
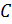
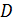
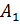
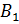
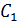
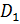
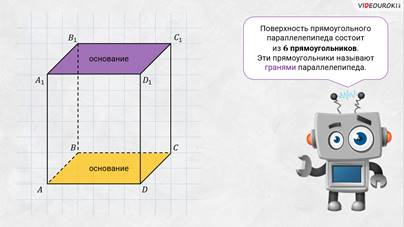
У любого прямоугольного параллелепипеда восемь 8 вершин. Так, у нашего прямоугольного параллелепипеда вершинами являются точки А, Бэ, Цэ, Дэ, А один, Бэ один, Цэ один и Дэ один.

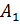
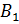
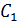
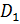
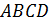
Поверхность прямоугольного параллелепипеда состоит из шести 6 прямоугольников. Эти прямоугольники называют гранями параллелепипеда. Так, у нашего параллелепипеда есть верхняя грань А один Бэ один Цэ один Дэ один, нижняя грань А Бэ Цэ Дэ. Эти грани ещё называют основаниями прямоугольного параллелепипеда.

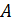
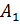
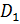
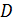
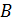
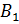
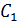
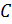
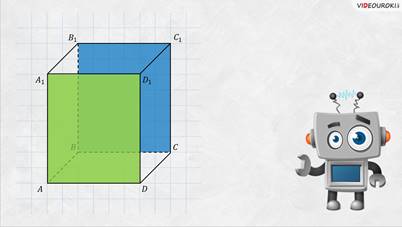
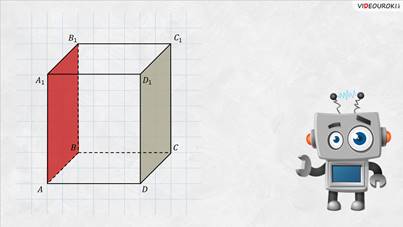
Дальше – передняя грань А А один Дэ один Дэ, задняя грань Бэ Бэ один Цэ один .Цэ

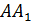
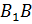
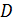
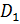
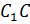
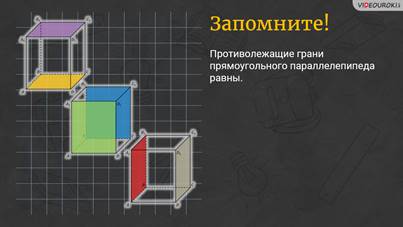
и И две боковые грани А А один Бэ один Бэ и Дэ Дэ один Цэ один Цэ.

Обратите внимание: грани, расположенные напротив друг друга, не имеют общих вершин. Такие грани называют противолежащими, или вы можете ещё услышать противоположными. Запомните! Противолежащие грани прямоугольного параллелепипеда равны.

– То есть в нашем параллелепипеде три 3 пары равных граней? – решил уточнить Саша.

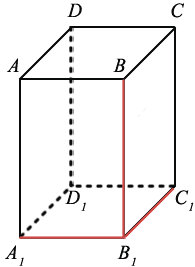
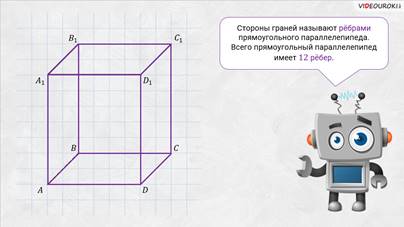
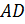
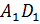
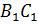
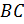
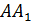
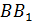
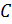
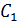
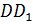
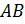
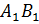
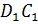
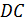
– Правильно! У прямоугольного параллелепипеда три 3 пары равных граней, – ответил Электроша. — Продолжим дальше рассматривать наш параллелепипед. Стороны граней называют рёбрами прямоугольного параллелепипеда. Всего прямоугольный параллелепипед имеет двенадцать 12 рёбер. Обратите внимание: рёбра А Дэ, А один Дэ один, Бэ один Цэ один и Бэ Цэ равны. Рёбра А А один, Бэ Бэ один, Цэ Цэ один и Дэ Дэ один тоже равны. Также равны и рёбра А Бэ, А один Бэ один, Дэ один Цэ один и Дэ Цэ.

– Электроша, получается, что у прямоугольного параллелепипеда восемь 8 вершин, шесть 6 граней и двенадцать 12 рёбер? – решил уточнить Паша.

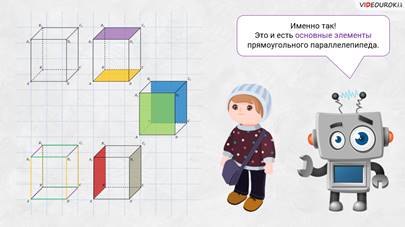
– Именно так, – подтвердил Электроша. — Это и есть основные элементы прямоугольного параллелепипеда.

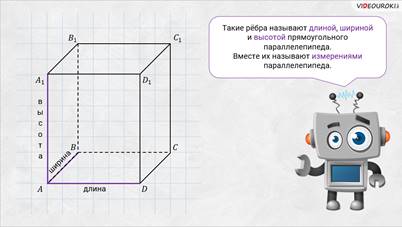
Посмотрите: в каждой вершине прямоугольного параллелепипеда сходятся три ребра. Такие рёбра называют длиной, шириной и высотой прямоугольного параллелепипеда. Вместе их называют измерениями параллелепипеда.

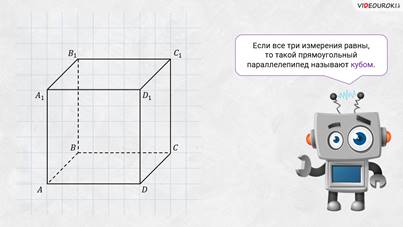
– Если все три измерения равны, то такой прямоугольный параллелепипед называют кубом, – продолжил Электроша. Нетрудно догадаться, что поверхность куба состоит из шести 6 равных квадратов. Кроме того, все двенадцать 12 рёбер куба также равны.

– Тела имеют разные свойства. Одним из свойств является масса, которую находят с помощью весов. А вот другим свойством тел является площадь поверхности.

– Это как площадь в прямоугольнике? – спросил Саша.

– Да, – ответил Электроша, – отличие лишь в том, что прямоугольный параллелепипед – это объёмная фигура, а так как прямоугольный параллелепипед имеет шесть 6 граней – прямоугольников, причём противолежащие грани его попарно равны, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей его шести 6 граней, при этом площади противолежащих граней будут равны. Запомните! Площадью поверхности параллелепипеда называют сумму площадей всех его граней. Если измерения нашего прямоугольного параллелепипеда обозначить таким образом: a – его длина, бэ b – ширина и цэ c – высота, то площадь его поверхности можно вычислить следующим образом: ….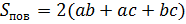

Если прямоугольный параллелепипед является кубом с длиной ребра равной а, то площадь его поверхность можно записать так: ….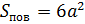

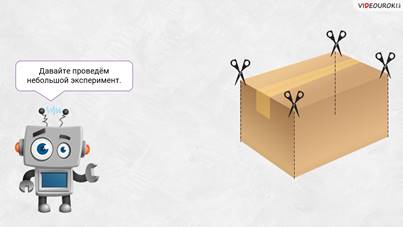
– А теперь давайте проведём небольшой эксперимент – предложил Электроша. — Возьмём коробку, имеющую форму прямоугольного параллелепипеда.

Откроем её, затем разрежем по четырём вертикальным рёбрам, а потом развернём.

– И что за странную фигуру мы получили? – спросил Саша.

– Фигуру, которая у нас получилась, называют развёрткой прямоугольного параллелепипеда. С помощью развёртки можно изготовить модель прямоугольного параллелепипеда.

Как вы думаете, вот такая развёртка какому геометрическому телу принадлежит?

– Да это же развёртка куба! – догадался Паша. — Она состоит из шести 6 равных квадратов.

– Молодец! – похвалил Пашу Электроша. — А теперь посмотрите на следующую картинку. Что вы видите на ней?

– Да это же одно из семи чудес света – египетские пирамиды, – воскликнули ребята, — нам про них рассказывали на уроках истории.

– Молодцы! – похвалил ребят Электроша. — Среди множества разнообразных геометрических тел есть большая группа, которая называется многогранниками.

Многогранники – это геометрические тела, поверхность которых состоит из многоугольников. Параллелепипед и пирамида являются видами многогранников.

– Электроша, а расскажи нам про пирамиды, – попросили робота мальчишки.

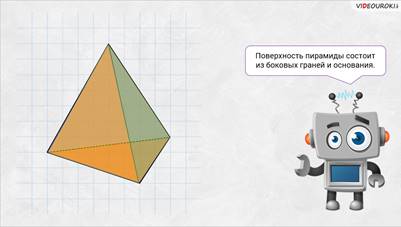
– С радостью, – улыбнулся Электроша. — Посмотрите на рисунок. На нём изображена пирамида.

Нетрудно заметить, что поверхность нашей пирамиды состоит из боковых граней и основания. Причём боковые грани пирамиды всегда являются треугольниками, имеющими общую вершину. Эту общую вершину боковых граней называют вершиной пирамиды. А стороны граней называют рёбрами пирамиды.

– Электроша, ты сказал, что пирамида состоит из боковых граней и основания и что все боковые грани — всегда треугольники. А что, в основании пирамиды может лежать не треугольник? – спросил Паша.

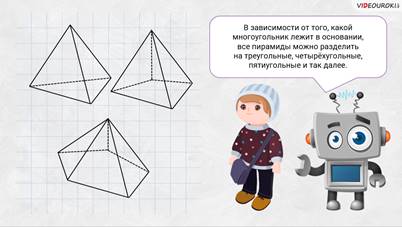
– Хороший вопрос! – обрадовался Электроша. — В основании пирамиды может лежать любой многоугольник. И в зависимости от того, какой многоугольник лежит в основании, все пирамиды можно разделить на треугольные, четырёхугольные, пятиугольные и так далее. Перед вами примеры таких пирамид.

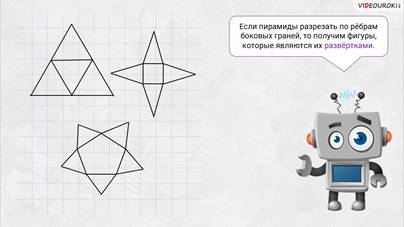
– Если пирамиды разрезать по рёбрам боковых граней, то получим фигуры, которые являются их развёртками.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

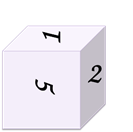
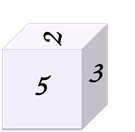
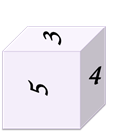
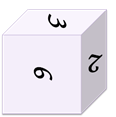
Задание первое: есть четыре изображения одного кубика с разных сторон.

Восстановите развёртку данного кубика по известной её части.

Решение: из первого изображения видно, что единичка 1 расположена над двойкой2. Рассматривая второе изображение кубика, можно сделать вывод, что тройка 3 расположена под двойкой2. Из следующего изображения делаем вывод, что четвёрка 4 расположена под тройкой3. А из последнего изображения можем заметить, что шестёрка 6 расположена справа от тройки3. Сопоставляя все сделанные выводы и часть развёртки, которая известна, получим следующую развёртку кубика…:

Следующее задание: Миша хочет покрасить деревянный брусок в форме прямоугольного параллелепипеда. Сколько потребуется краски, если измерения этого бруска два 2 сантиметра, три 3 сантиметра, четыре 4 сантиметра и известно, что для покраски одного квадратного сантиметра поверхности потребуется два 5 грамма краски?

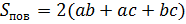
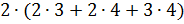
Решение: прежде чем узнать, сколько понадобится краски, нужно вычислить площадь поверхности бруска. Так как брусок имеет форму прямоугольного параллелепипеда, то можем воспользоваться формулой площади поверхности прямоугольного параллелепипеда: …. Подставим измерения нашего бруска в формулу. Получим: два умножить на сумму произведений двух и трёх, двух и четырёх, трёх и четырёх. Посчитаем и получим, что площадь поверхности нашего бруска равна пятидесяти двум52 квадратным сантиметрам.

Из условия задачи мы знаем, что на один 1 квадратный сантиметр поверхности потребуется два 2 грамма краски. Значит, 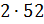два умножим на пятьдесят два. Получим сто четыре104 грамма.

Ответ: сто четыре104 грамма краски потребуется для покраски бруска.

– Паша, Саша, молодцы! – воскликнул Электроша. — Ну и давайте напоследок повторим, что нового вы сегодня узнали.

Многогранники – это геометрические тела, поверхность которых состоит из многоугольников.

Параллелепипед и пирамида являются видами многогранников.

Прямоугольный параллелепипед – это многогранник, поверхность которого состоит из шести прямоугольников.

У прямоугольного параллелепипеда восемь вершин, шесть граней и двенадцать рёбер.

Грани прямоугольного параллелепипеда, расположенные напротив друг друга и не имеющие общих вершин, называют противолежащими.

Противолежащие грани прямоугольного параллелепипеда равны.

Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, называют измерениями (длиной, шириной и высотой).

Если все три измерения равны, то такой прямоугольный параллелепипед называют кубом.

Площадью поверхности параллелепипеда называют сумму площадей всех его граней.

Пирамида – это многогранник, у которого все боковые грани — треугольники.

В зависимости от того, какой многоугольник лежит в основании, все пирамиды можно разделить на треугольные, четырёхугольные, пятиугольные и так далее.

Источник