какие графики пересекаются а какие параллельны
Взаимное расположение графиков линейных функций. 7-й класс
Класс: 7
Презентация к уроку
1. Организационный момент.
На этом уроке мы продолжим говорить о линейной функции и о прямой пропорциональности. Выясним их взаимное расположение, зависящее от значений k и b. Научимся по внешнему виду, не выполняя построений определять взаимное расположение графиков линейных функций. Каждый на уроке обязательно получит оценку.
2. Актуализация знаний.
б) В это время 2 человека работают по карточкам.
3. Проверка домашнего задания.
1) Найти координаты точки пересечения графиков линейных функций:
2) Построить в одной системе координат графики функций:
Работа устная по чертежам. Вывод записать в тетрадь.
4. Закрепление. Устно.
1) Определить по графику знак углового коэффициента k и число b

k • 0 + 4 = 4
2) График функции у = kх + 5 проходbт через точку М(-7; 12). Найдите k.
1. Не выполняя построения, определите взаимное расположение графиков функций:
а) у = 2х –1 и у = 2х + 3
А) пересекаются
Б) параллельны
В) совпадают
б) у = 3х + 2 и у = 2х –3
А) пересекаются
Б) параллельны
В) совпадают
в) у = 0,5х + 

А) пересекаются
Б) параллельны
В) совпадают
2. Подберите и вставьте вместо знака вопроса такое число, чтобы графики функций:
3.Составить функцию для графика, изображенного на рисунке:
1. Не выполняя построения, определите взаимное расположение графиков функций:
а) у = 6х – 1 и у = 4х + 5
А) пересекаются
Б) параллельны
В) совпадают
А) пересекаются
Б) параллельны
В) совпадают
в) у = 0,5х + 2 и у = 0,5х – 4
А) пересекаются
Б) параллельны
В) совпадают
2. Подберите и вставьте вместо знака вопроса такое число, чтобы графики функций:
3.Составить функцию для графика, изображенного на рисунке:
6. Домашнее задание: № 335, 336, 346, 347/
7. Итог урока.(выставление оценок, рефлексия)
График линейной функции, его свойства и формулы
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Задание 9 ЕГЭ по математике. Графики функций
В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №9 ЕГЭ.
Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 9 в формате ЕГЭ-2021
Линейная функция
Вычтем из первого уравнения второе:
Уравнение прямой имеет вид:
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Запишем формулы функций.
Вычтем из первого уравнения второе.
Прямая задается формулой:
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
Для прямой, расположенной выше, угловой коэффициент равен
Эта прямая проходит через точку (-2; 4), поэтому: эта прямая задается формулой
Для точки пересечения прямых:
Квадратичная функция. Необходимая теория
4. На рисунке изображен график функции Найдите b.
На рисунке — квадратичная парабола полученная из графика функции сдвигом на 1 вправо, то есть
6. На рисунке изображён график функции Найдите
Формула функции имеет вид:
7. На рисунке изображены графики функций и которые пересекаются в точках А и В. Найдите абсциссу точки В.
Найдем абсциссу точки B. Для точек A и B:
(это абсцисса точки A) или (это абсцисса точки B).
Степенные функции. Необходимая теория
График функции проходит через точку (2; 1); значит,
Для точек A и B имеем:
Отсюда (абсцисса точки A) или (абсцисса точки B).
Функция задана формулой:
Ее график проходит через точку (4; 5); значит,
Показательная функция. Необходимая теория
11. На рисунке изображён график функции Найдите
График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции получим:
Поделим второе уравнение на первое:
Подставим во второе уравнение:
График функции проходит через точку Это значит, что
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции Найдите
График функции проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
Вычтем из второго уравнения первое:
или — не подходит, так как (как основание логарифма).
Тригонометрические функции. Необходимая теория
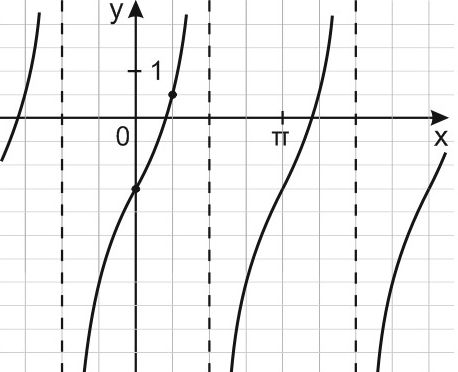
15. На рисунке изображён график функции Найдите
График функции сдвинут на 1,5 вверх; Значит, Амплитуда (наибольшее отклонение от среднего значения).
16. На рисунке изображён график функции
На рисунке — график функции Так как
График функции проходит через точку A Подставим и координаты точки А в формулу функции.
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если то
Друзья, мы надеемся, что на уроках математики в школе вы решаете такие задачи. Для углубленного изучения темы «Функции и графики» (задание 9 ЕГЭ по математике), а также задач с параметрами и других тем ЕГЭ — рекомендуем Онлайн-курс для подготовки к ЕГЭ на 100 баллов.
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
§ 10. Взаимное расположение графиков линейных функций
Теорема 5.
Пусть даны две линейные функции у = k1x + m1 и у = k2x + m2. Прямые, служащие графиками заданных линейных функций:
3) пересекаются, если k1 ≠ k2.
Пример 1. Найти точку пересечения прямых:
Для линейной функции 
Прямая l2 служащая графиком линейной функции 
Прямые l1 и l2 пересекаются в точке (2; 1).
Во-вторых, как одна, так и другая прямая проходят через точку (0; 7) (вы обратили внимание, что m1 = m2 = 7?).
Следовательно, (0; 7) и есть искомая точка пересечения.
Вообще прямые у = kx1 + m и у = k2x + m, где k1 ≠ k2, пересекаются в точке (0; m).
Вопросы для самопроверки
1. Приведите пример линейных функций, графики которых параллельны.
2. Приведите пример линейных функций, графики которых совпадают.
3. Приведите пример линейных функций, графики которых пересекаются.
4. Что вы можете сказать о взаимном расположении на координатной плоскости хОу графиков линейных функций:
5. Как будет расположен график функции у = 4х + а относительно графика функции у = 4x, если а > 0? если а
Урок алгебры в 7-м классе по теме: «Взаимное расположение графиков линейных функций»
Разделы: Математика
Подведение итогов урока.
Ход урока
1. Организационный момент.
Да, путь познания не гладок,
Но знаем мы со школьных лет,
Загадок больше,чем отгадок
И поискам предела нет.
2. Актуализация опорных знаний.
| Вопрос учителя | Ответ ученика |
| Рассмотрите рисунок 2. Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка? Почему? | Ученик допустил ошибку при построении графика функции у=1,5х, так как это график прямой пропорциональности,проходит через начало координат. |
| Вопрос учителя | Ответ ученика |
| На рисунке изображены графики функций у=2х,у=-2х,у=х+2. Рассмотрите расположение прямых в координатной плоскости и укажите, какая формула соответствует каждой из них. |
Подведение итога.
Сообщение темы урока, цели.
Выполнение работы.
Подведение итогов.
Первичное закрепление.
На доске ряд линейных функций. Не выполняя построения графиков, назовите пары функций, графики которых параллельны, пересекаются, перпендикулярны.
У=2х – 4, у=-4х + 2, у= 2х +3, у=2х, у= 7х – 8, у=5х +2.
Работа с учебником.
Прочитать вывод в учебнике с. 65, рассмотреть рисунки 31, 32.
Работа с учебником самостоятельно №335.
Постановка домашнего задания.
Подведение итогов урока.
Если угловые коэффициенты двух линейных функций не равны,то прямые, являющиеся их графиками, пересекаются;
если произведение угловых коэффициентов равно (-1), то прямые, являющиеся их графиками, перпендикулярны.
Приложение 1
На изучение темы “Линейная функция” отводится 9 часов. Данный урок является 6 в теме.