какие геометрические тела вам известны
Геометрические тела.
Геометрическое тело — часть пространства, которая ограничена замкнутой поверхностью своей наружной
Геометрическое тело возможно выделить замкнутой поверхностью, т.е. его границей.
Еще геометрическим телом можно назвать компактное множество точек, и 2 точки из множества
возможно соединить отрезком, этот отрезок целиком проходит внутри границы тела, это указывает на то,
что геометрическое тело состоит из множества внутренних точек.
Наружная граница геометрического тела является его гранью, у тела может быть одна либо несколько
граней. Множество плоских граней определяет множество вершин и ребер геометрического тела.
Все геометрические тела делятся на многогранники и тела вращения.
Тела вращения.
Тела вращения — это объёмные тела, которые возникают следствием вращения плоской геометрической
фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости.
Если вращать контуры фигур, образуется поверхность вращения (к примеру, сфера, которая
образовывается из окружности), а если вращать заполненные контуры – возникают тела (шар, который
Шар — образуется из полукруга, вращением вокруг диаметра разреза.

Цилиндр — образуется из прямоугольника, вращая его вокруг одной из
Площадью боковой поверхности цилиндра берут площадь его развертки:

вокруг одного из катетов.
Площадью боковой поверхности конуса берут площадь ее развертки:
Площадь полной поверхности конуса:

Тор (тороид) — образуется из окружности, вращая ее вокруг прямой, которая не

Многогранники.
Многогранник или полиэдр — зачастую замкнутая поверхность, состоящая из многоугольников. Ее,
бывает, зовут тело, которое ограничено этой поверхностью.
Многогранник – тело, у которого граница, это объединение ограниченного количества многоугольников.
Есть 5 видов правильных многогранников:
| Тетраэдр |  |
| Гексаэдр (куб) |  |
 | |
| Додекаэдр |  |
 |
Правильным многогранником является многогранник, с гранями из правильных равных многоугольников,
также, каждый двугранный угол имеет одинаковое значение.
Однако существуют другие многогранники – все многогранные углы равны, а грани – правильные, при этом
разноименные правильные многоугольники. Такие многогранники являются
равноугольно-полуправильными многогранниками.
усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный
додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр,
ромбокубооктаэдр, ромбоикосододекаэдр, «плосконосый» (курносый) куб, «плосконосый»
получить правильные звездчатые многогранники.
Таких многогранников существует только 4, еще их зовут телами Кеплера-Пуансо. Кеплер открыл
малый додекаэдр, и назвал его «колючий» либо «еж», и большой додекаэдр. Пуансо открыл другие 2
правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
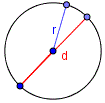
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Какие геометрические тела бывают
Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. Практическая деятельность человека служила основой открытия простейших геометрических зависимостей и соотношений.
Многогранники
В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения.
Поверхность составленную из многоугольников и ограничивающую некоторое геометрическое тело, будет называть многогранной поверхностью или многогранником. Виды многогранников: параллелепипед, призма, пирамида.
Призма
Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и параллелограммов, называется призмой. Многоугольники называются основаниями, а параллелограммы – боковыми гранями призмы. Отрезки называются боковыми ребрами призмы.
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой.
Параллелепипед
Если в основании призмы лежит параллелограмм, то призма называется параллелепипедом. Параллелепипеды бывают наклонные, прямые и прямоугольные.
Прямоугольный параллелепипед имеет три измерения: длину, высоту и ширину. У параллелепипеда 8 вершин, 12 ребер, 6 граней. Каждая грань параллелепипеда – прямоугольник. Противоположенные грани параллелепипеда равны. Среди всех параллелепипедов особую роль играет куб. Куб – это прямоугольный параллелепипед, у которого все стороны равны. Все его грани – квадраты.
Пирамида
Важным и интересным семейством многогранников является пирамида. У пирамиды различают основание и боковые грани. Боковые грани – треугольники, сходящиеся в одной вершине, а основание – многоугольник, противолежащий этой вершине. В основании может лежать многоугольник с любым количеством сторон. Пирамиду называют по числу сторон ее основания: треугольная пирамида, четырехугольная пирамида, шестиугольная пирамида… Простейшей пирамидой и даже простейшем многогранником является треугольная пирамида. Все ее грани – треугольники, и каждая из них может считаться основанием.
Пирамида называется правильной, если ее основание – правильный многоугольник, и вершина пирамиды проектируется в центр этого многоугольника. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Правильные многогранники
Правильным называют многогранник, все грани которого – равные правильные многоугольники и в каждой вершине сходится одинаковое число граней.
Виды правильных многоугольников
Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников.
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников.
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников.
Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов.
Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая его вершина является вершиной трех правильных пятиугольников.
Круглые тела
Круглые тела имеют круглую форму. Также могут состоять из нескольких окружностей, круглые тела образуются с помощью вращения квадратной плоскости. В таких фигурах также есть свои особенности, например, существует сложные круглые тела. Примеры круглых тел: цилиндр, конус, сфера и шар.
Цилиндр
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра.
Прямая, проходящая через центры оснований, называется осью цилиндра.
Длина образующей называется высотой, а радиус основания – радиусом цилиндра.
Конус
Тело, ограниченное конической поверхностью и кругом с границей, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.
Усеченный конус
Часть конической поверхности, ограничивающая конус, называется ее боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называется образующими усеченного конуса. Все образующие усеченного конуса равны друг другу.
Шар и сфера
Сферой называют поверхность, состоящая из все точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а донное расстояние радиусом сферы.
Тело, ограниченное сферой называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Справочник по теме «Геометрические тела»
Ищем педагогов в команду «Инфоурок»
Выполнил: Давыдов Антон, ученик 11-го класса
Шар — это объемная геометрическая фигура,
ограниченная поверхностью, все точки которой
находятся на одинаковом расстоянии от центра;
образуется из полукруга, вращением
вокруг диаметра разреза.
Площадь поверхности: S = 4πR2
Объем шара: V = 4/3 πR 3
ограниченное цилиндрической поверхностью
и двумя параллельными плоскостями,
пересекающими её; образуется из
прямоугольника, вращая его вокруг одной из
Площадь боковой поверхности:
Площадь основания цилиндра:
Площадь поверхности цилиндра:
S = Sбок.пов + 2Sосн = 2πR h + 2πR^2
Объем цилиндра: V = Sосн ⋅ H = πR^2H
всех лучей, исходящих из одной точки
(вершины конуса) и проходящих через
плоскую поверхность; образуется из
прямоугольного треугольника, при
вращении его вокруг одного из катетов.
Образующую конуса: L = √ H ^2 + R^2
Площадь боковой поверхности: Sбок.пов = πRL
Площадь основания конуса: Sосн = πR^2
Объем конуса: V = 1/3πR^2h
получаемая вращением образующей
окружности вокруг оси, лежащей в плоскости
этой окружности и не пересекающей её.
r — радиус образующей окружности тора;
R — радиус вращения образующей окружности.
гранями которого являются четыре
Основные формулы для правильного тетраэдра:
Куб – это прямоугольный параллелепипед,
все стороны (ребра) которого равны.
Основные формулы для куба:
Октаэдр — многогранник с восемью гранями.
Основные формулы для октаэдра:
Додекаэдр – это объемная геометрическая
фигура, которая имеет 12 граней.
Основные формулы для додекаэдра:
Икосаэдр — правильный выпуклый
Основные формулы для икосаэдра:
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
В справочнике отражены все геометрические формулы геометрических тел, их объёмы, площади полной и боковой поверхности. Работа содержит рисунок геометрического тела и краткую информацию о нем.
Справочник является продуктом проекта «Геометрические тела» и очень полезен для учащихся в подготовке к ГИА.
Номер материала: ДБ-596378
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников
Время чтения: 1 минута
Минпросвещения планирует прекратить прием в колледжи по 43 профессиям
Время чтения: 1 минута
Почти все вузы в России открыли пункты вакцинации от ковида
Время чтения: 1 минута
Школьников не планируют переводить на удаленку после каникул
Время чтения: 1 минута
В школе в Пермском крае произошла стрельба
Время чтения: 1 минута
Минобрнауки разрешило вузам перейти на дистанционное обучение
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.