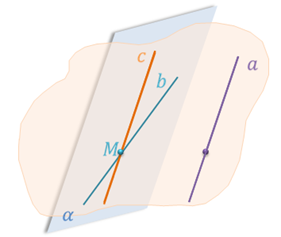
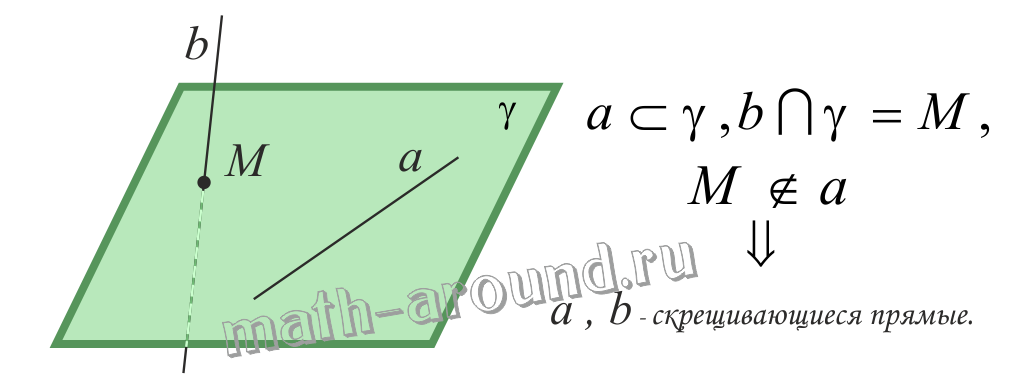какие две прямые в пространстве называют скрещивающимися

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

Скрещивающиеся прямые. Расположение прямых в пространстве.

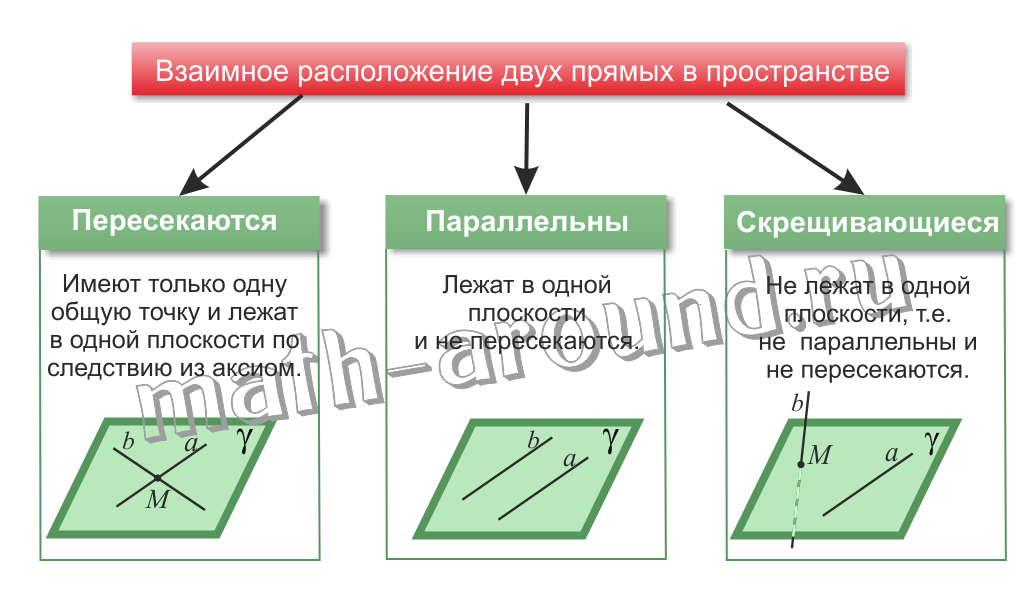
Если две прямые в пространстве параллельны или пересекаются, то они лежат в одной плоскости.
Возможен еще один случай взаимного расположения в пространстве, когда прямые не лежат в одной плоскости.

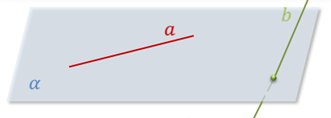
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых.

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Теорема о скрещивающихся прямых.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Автор: Аникина Марина

Комментарии к этой заметке:

Добавить Ваш комментарий

Хотите внести свою лепту в его развитие!? Тогда Вам сюда!

Источник

2. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми

Скрещивающиеся прямые

Нам известны два случая расположения прямых в пространстве a ∩ b; а || b. Общее для них: они лежат в одной плоскости (рис. 1, 2).

(по следствию из аксиомы)

(по определению параллельных прямых)

ЗАДАНИЕ №1 в рабочей тетради

Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).

Доказать, что АВ скрещивается с CD.

Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.

Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.

ЗАДАНИЕ №2 в рабочей тетради

Теорема :

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.

Дано: АВ скрещивается CD (рис. 6).

Построить α: АВ ⊂ α, CD || α.

1. Через точку А проведем прямую АЕ, АЕ || CD.

В доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.

Задание №3-№4 в рабочей тетради

Углы с сонаправленными сторонами. Угол между прямыми

Любая прямая а, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей.

Источник

Скрещивающиеся прямые

Урок 7. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Скрещивающиеся прямые»

· дадим определение скрещивающихся прямых;

· рассмотрим возможные случаи взаимного расположения двух прямых в пространстве;

· докажем теорему, которая выражает признак скрещивающихся прямых

· докажем теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

Для начала давайте вспомним определение параллельных прямых в пространстве. Итак, две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

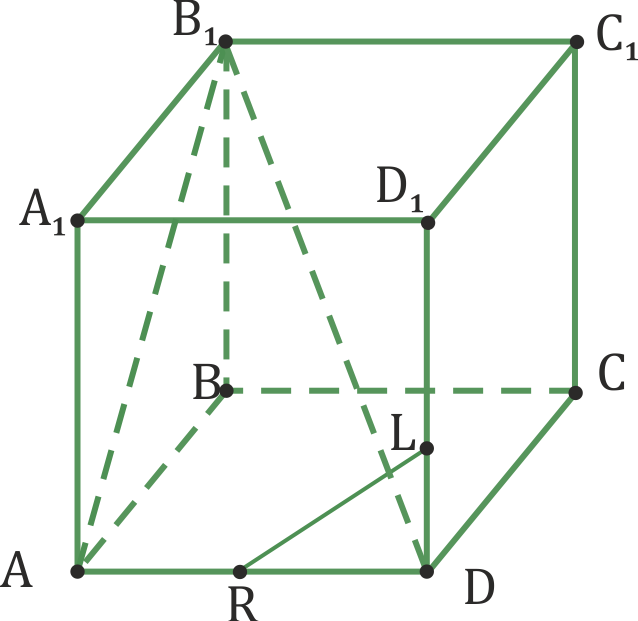
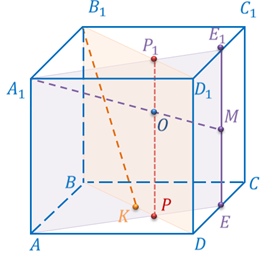
Давайте рассмотрим все тот же наш любимый куб ABCDA₁B₁C₁D₁.

Понятно, что прямые, на которых лежат его ребра AB и DC параллельны, ведь они лежат в одной плоскости, например, ABC и не пересекаются.

Проведем диагонали AB₁A₁B грани AA₁B₁B. Видно, что прямые на которых лежат указанные диагонали расположены в одной плоскости AA₁B₁ и пересекаются.

Теперь давайте проведем диагональ куба B₁D. И попытаемся разобраться о взаимном расположении прямых, на которых лежат диагональ B₁D и ребро AA₁. Обратите внимание, что нет такой плоскости, которая проходила бы через обе эти прямые. Значит, параллельными они быть не могут, по определению параллельности прямых в пространстве. Пересекаться также не могут, так как не лежат в одной плоскости.

Для такого случая расположения прямых также есть название. Такие прямые называют скрещивающимися.

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

На экране изображены скрещивающиеся прямые а и b. Их обозначают следующим образом .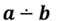

Итак, возможны три случая взаимного расположения двух прямых в пространстве:

1. прямые пересекаются, т.е. имеют одну только общую точку.

2. прямые параллельны, т.е. лежат в одной плоскости и не пересекаются.

3. прямые скрещивающиеся, т.е. не лежат в одной плоскости, не параллельны и не пересекаются.

Наглядным примером о скрещивающихся прямых дают две дороги, одна из которых проходит по эстакаде, а другая – под эстакадой.

Линии электропередач и река. Они также дают нам представление о скрещивающихся прямых.

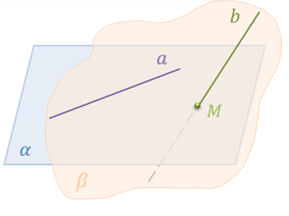
Докажем теорему, которая позволяет выяснить, являются ли две прямые скрещивающимися. Эту теорему называют признаком скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Доказательство. Пусть прямая а лежит в плоскости α, а прямая b пересекает эту плоскость в точке М, не лежащей на прямой а. Докажем, что прямые а и b скрещиваются, т.е. не существует плоскость, в которой они обе лежат.

Предположим, что прямые а и b лежат в некоторой плоскости β. Тогда плоскость β проходит через прямую а и точку М, а следовательно, совпадает с плоскостью α (так как через прямую и не лежащую на ней точку проходит единственная плоскость).

Получили, что прямая b лежит в плоскости α, а это противоречит условию теоремы.

Таким образом, наше предположение неверно, а значит, прямые а и b – скрещивающиеся.

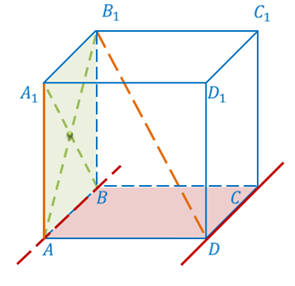
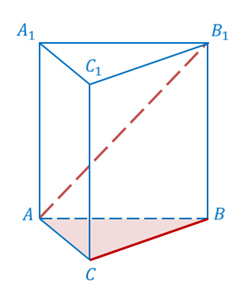
Рассмотрим пример. Пусть ABCA₁B₁C₁ – прямая треугольная призма.

Тогда прямые AB₁ и BC – скрещивающиеся, так как прямая AB₁ пересекает плоскость ABC в точке А, не лежащей на прямой BC.

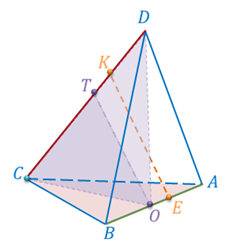
Задача. Точки и лежат на ребре , а точки и на ребре тетраэдра . Докажите, что прямые и – скрещивающиеся.

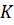
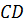
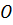
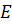
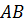
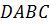
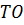
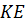
Доказательство. Прямая ТК пересекает плоскость ABC в точке C, не лежащей на прямой ОЕ, следовательно, прямые ТК и ОЕ скрещивающиеся. Значит, точки Т, К, Е и О не лежат в одной плоскости. Обратите внимание, прямая ТО лежит в плоскости ТОC. КЕ пересекает плоскость ТОC в точке К. Точка К не принадлежит прямой ТО. Отсюда следует, что прямые ТО и КЕ не лежат в одной плоскости, т.е. по признаку скрещивающихся прямых они являются скрещивающимися. Что и требовалось доказать.

Докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство. Пусть а и b скрещивающиеся прямые. Докажем, что через прямую b проходит плоскость, параллельная прямой а. Через какую-либо точку М прямой b проведем прямую c, параллельную прямой а.

Пусть α– плоскость, проходящая через прямые b и c. Так как прямая а не лежит в плоскости α и параллельна прямой c, лежащей в этой плоскости, то прямая а параллельна плоскости α.

Понятно, что плоскость α – единственная плоскость, проходящая через прямую b и параллельная прямой а. Действительно, любая другая плоскость, проходящая через прямую b, пересекается с прямой c, а следовательно, пересекается и с параллельной ей прямой а. Теорема доказана.

Наглядным примером этой теоремы служат две дороги, одна из которых проходит по эстакаде, а другая – под эстакадой. Нижняя дорога лежит в плоскости земли, параллельной дороге на эстакаде. Ясно, что и через дорогу на эстакаде проходит плоскость, параллельная плоскости земли, а значит, параллельная нижней дороге.

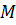
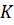
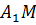
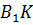
Задача. Точки и – центры граней куба. Докажите, что прямые и скрещиваются

Что и требовалось доказать.

Подведем итоги урока. На этом уроке мы дали определение скрещивающихся прямых. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Рассмотрели три возможных случая взаимного расположения двух прямых в пространстве. Доказали теорему, которая выражает признак скрещивающихся прямых. А также доказали теорему о том, что через каждую из скрещивающихся прямых можно провести плоскость, параллельную другой прямой.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №5. Взаимное расположение прямых в пространстве

Перечень вопросов, рассматриваемых в теме

Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Два отрезка называются параллельными, если они лежат на паралельных прямых.

Открытый электронный ресурс:

Теоретический материал для самостоятельного изучения

Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые

На прошлом уроке в качестве наглядного примера нами был приведен куб.

Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.

Примеры скрещивающихся прямых вокруг нас:

Одна дорога проходит по эстакаде, а другая под эстакадой

Горизонтальные линии крыши и вертикальные линии стен

Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.

Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).

Рисунок 2 – скрещивающиеся прямые АВ и СD

Итак, возможны три случая расположения прямых в пространстве:

Разберем и докажем еще одну теорему о скрещивающихся прямых.

Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)

1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ

Любая прямая, например ОО₁, рассекает плоскость на две полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат в одной полуплоскости, то они называются сонаправленными.

Лучи О₁А₁ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи

Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)

Доказательство:

при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.

Отметим на сторонах угла O произвольные точки A и B.

На соответствующих сторонах угла O₁ отложим отрезки OA₁ и O₁B₁ равные соответственно ОA и OB.

2. В плоскости рассмотрим четырехугольник OAA₁O₁.

Так как противолежащие стороны OA и O₁A₁ этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA₁ и OO₁.

3. В плоскости, аналогично можно доказать, что OBB₁O₁ параллелограмм, поэтому равны и параллельны стороны ВВ₁ и OO₁.

4. Если две отрезка AA₁ и BB₁ равны параллельны третьему отрезку OO₁, значит, они равны и параллельны, т. е. АА₁||BB₁ и AA₁ = BB₁.

По определению четырехугольник АВВ₁А₁ – параллелограмм и из этого получаем АВ=А₁В₁.

5.Из выше построенного и доказанного АВ=А₁В₁, ОA =O₁A₁ и OB =O₁B₁ следует, что треугольники AOB и A₁ O₁ B₁. равны по трем сторонам, и поэтому О= О₁.

Рисунок 5 – равные углы с сонаправленными сторонами

Источник

Какие две прямые в пространстве называют скрещивающимися

Прямые линии в пространстве могут быть параллельными , пересекающимися и скрещивающимися . Рассмотрим подробнее каждый случай.

1. Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Рисунок 33. Параллельные прямые

Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 3 4 ). В рассмотренном случае проекции отрезков на плоскость П ₃ пересекаются, следовательно, они не параллельны.

Решение этого вопроса можно получить сравнением двух соотношений если:

Рисунок 34. Прямые параллельные профильной плоскости проекций

2. Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 3 5 ).

Рисунок 35. Пересекающиеся прямые

В общем случае справедливо и обратное утверждение, но есть два частных случая:

1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.3 6 ), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.

2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 3 7 ).

О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции ( А ₁В₁ ∩ С ₁D₁ Þ АВ ∩ СD ).

3. Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.

Источник