какие две прямые называют перпендикулярными в пространстве

Перпендикулярные прямые на плоскости: определение и доказательство теоремы

Что такое перпендикулярные прямые, в чём их особые свойства и почему через точку на прямой можно провести только один перпендикуляр.

Понятие перпендикулярных прямых

Углы бывают острые, прямые и тупые.

Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Изучайте математику вместе с преподавателями домашней онлайн-школы «Фоксфорда»! По промокоду GEOM72021 вы получите неделю бесплатного доступа к курсу геометрии 7 класса, в котором изучаются перпендикулярные прямые!

Теорема о перпендикулярных прямых

Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну.

Построим доказательство теоремы о перпендикулярных прямых «от противного», то есть для начала предположим, что утверждение неверно.

Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.

Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA, равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.

Свойство перпендикулярных прямых

Две прямые, перпендикулярные третьей, не пересекаются.

Пусть a⟂b и a⟂c. b и с не пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.

У нас вы сможете учиться в удобном темпе, делать упор на любимые предметы и общаться со сверстниками по всему миру.

Попробовать бесплатно

Интересное по рубрике

Найдите необходимую статью по тегам

Подпишитесь на нашу рассылку

Мы в инстаграм

Домашняя онлайн-школа
Помогаем ученикам 5–11 классов получать качественные знания в любой точке мира, совмещать учёбу со спортом и творчеством

Посмотреть

Рекомендуем прочитать

Реальный опыт семейного обучения

Звонок по России бесплатный

Посмотреть на карте

Если вы не нашли ответ на свой вопрос на нашем сайте, включая раздел «Вопросы и ответы», закажите обратный звонок. Мы скоро свяжемся с вами.

Источник

Перпендикулярные прямые, условие перпендикулярности прямых

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

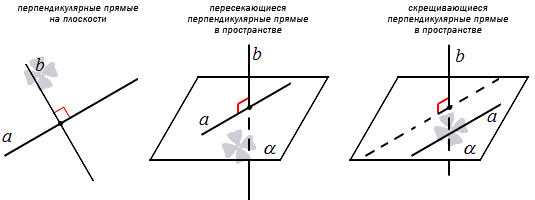
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Очевидно, что необходимое и достаточное условие выполнимо, значит, А В и А С перпендикулярны.

Ответ: прямые перпендикулярны.

Решение

Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.

Ответ: прямые не перпендикулярны.

Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.

Ответ: прямые перпендикулярны.

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Необходимое и достаточное условие было выполнено.

Ответ: прямые перпендикулярны.

Ответ: заданные прямые перпендикулярны.

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Источник

Перпендикулярность прямой и плоскости (ЕГЭ 2022)

В пространстве перпендикулярными могут быть:

Давай для полного понимания рассмотрим не только перпендикулярность прямой и плоскости, а все три случая перпендикулярности в пространстве.

Все относящиеся к ним определения и формулировки теорем.

А потом обсудим очень важную теорему о трёх перпендикулярах.

И ты будешь знать о перпендикулярности в пространстве все!

Поехали!

Перпендикулярность в пространстве — коротко о главном

Перпендикулярность двух прямых

Две прямые в пространстве перпендикулярны, если угол между ними \( 90<>^\circ \).

Перпендикулярность прямой и плоскости

Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.

Перпендикулярность плоскостей

Плоскости перпендикулярны, если двугранный угол между ними равен \( 90<>^\circ \).

Критерий перпендикулярности плоскостей

Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.

Теорема о трех перпендикулярах

Прямая \( a\), не лежащая в плоскости \( \alpha \), перпендикулярна прямой \( b\), лежащей в плоскости \( \alpha \), тогда и только тогда, когда проекция \( a\prime \) прямой a перпендикулярна прямой \( b\).

Перпендикулярность двух прямых

Определение:

Две прямые в пространстве перпендикулярны, если угол между ними \( \displaystyle 90<>^\circ \).

Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.

На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):

А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:

Прямая \( \displaystyle a\) перпендикулярна прямой \( \displaystyle b\), хотя и не пересекается с нею. Как так?

Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми \( \displaystyle a\) и \( \displaystyle b\), нужно через произвольную точку \( \displaystyle O\) на прямой a провести прямую \( \displaystyle ’\parallel b\).

И тогда угол между \( \displaystyle a\) и \( \displaystyle b\) (по определению!) будет равен углу между \( \displaystyle a\) и \( \displaystyle <’>\).

Вспомнили? Ну вот, а в нашем случае – если окажутся перпендикулярны прямые \( \displaystyle a\) и \( \displaystyle <’>\), то нужно считать перпендикулярными прямые \( \displaystyle a\) и \( \displaystyle b\).

Для полной ясности давай рассмотрим пример

Эти прямые не пересекаются – они скрещиваются. Чтобы найти угол между \( \displaystyle AC\) и \( \displaystyle <_<1>><_<1>>\), проведём \( \displaystyle BD\).

Из-за того, что \( \displaystyle B<_<1>><_<1>>D\) — параллелограмм (и даже прямоугольник!), получается, что \( \displaystyle <_<1>><_<1>>\parallel BD\).

А из-за того, что \( \displaystyle ABCD\) – квадрат, выходит, что \( \displaystyle AC\bot BD\). Ну, и значит \( \displaystyle AC\bot <_<1>><_<1>>\).

Перпендикулярность прямой и плоскости

Определение:

Прямая \( \displaystyle h\) перпендикулярна плоскости \( \displaystyle \alpha \), если она перпендикулярна всем-всем прямым в этой плоскости: и \( \displaystyle a\), и \( \displaystyle b\), и \( \displaystyle c\), и даже \( \displaystyle d\)!

И ещё миллиарду других прямых!

Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит!

Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

Если найдутся всего лишь две пересекающиеся прямые (\( \displaystyle a\) и \( \displaystyle b\)) в плоскости \( \displaystyle\alpha\), которым перпендикулярна прямая \( \displaystyle h\), то эта прямая сразу окажется перпендикулярна плоскости \( \displaystyle \alpha \),

То есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой \( \displaystyle c\)).

Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.

Что это за арка? Это значок «пересечение»! Хороший способ быстрее писать конспекты 🙂

Прямая перпендикулярна двум пересекающимся прямым!

И опять рассмотрим пример

Пусть нам дан правильный тетраэдр \( \displaystyle ABCD\).

Задача: доказать, что \( \displaystyle BD\bot AC\).

Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!

Давай отметим середину \( \displaystyle M\) ребра \( \displaystyle AC\) и проведём \( \displaystyle BM\) и \( \displaystyle DM\).

Это медианы в \( \displaystyle \Delta ABC\) и \( \displaystyle \Delta ADC\).

Треугольники – правильные \( \displaystyle \Rightarrow BM\bot AC\) и \( \displaystyle DM\bot AC\).

Вот оно, чудо: получается, что \( \displaystyle AC\bot BMD\), так как \( \displaystyle AC\bot BM\) и \( \displaystyle AC\bot DM\).

И далее, \( \displaystyle AC\bot BMD\Rightarrow AC\bot \) всем прямым в плоскости \( \displaystyle BMD\), а значит, и \( \displaystyle AC\bot BD\).

И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.

Перпендикулярность плоскостей

Определение:

Плоскости перпендикулярны, если двугранный угол между ними равен \( \displaystyle 90<>^\circ \).

То есть (подробнее смотри в теме «двугранный угол») две плоскости (\( \displaystyle \alpha\) и \( \displaystyle \beta\)) перпендикулярны, если окажется, что угол между двумя перпендикулярами (\( \displaystyle a\) и \( \displaystyle b\)) к линии пересечения этих плоскостей равен \( \displaystyle 90<>^\circ \).

И есть теорема, которая связывает понятие перпендикулярных плоскостей с понятием перпендикулярность в пространстве прямой и плоскости.

Теорема эта называется: Критерий перпендикулярности плоскостей.

Критерий перпендикулярности плоскостей

Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.

Как всегда, расшифровка слов «тогда и только тогда» выглядит так:

(естественно, здесь \( \displaystyle \alpha \) и \( \displaystyle \beta \) — плоскости).

Теорема о трёх перпендикулярах

Эта теорема – одна из самых важных в стереометрии, но, к сожалению, и одна из самых непростых в применении.

Так что нужно быть очень внимательным!

Прямая \( \displaystyle a\), не лежащая в плоскости \( \displaystyle \alpha \), перпендикулярна прямой \( \displaystyle b\), лежащей в плоскости \( \displaystyle \alpha \), тогда и только тогда, когда проекция \( \displaystyle <’>\) прямой a перпендикулярна прямой \( \displaystyle b\).

И снова расшифровка слов «тогда и только тогда». Теорема утверждает сразу две вещи (смотри на картинку):

Давай попробуем применить эту теорему для решения задачи.

Задача: дана правильная шестиугольная пирамида \( \displaystyle SABCDEF\). Найти угол между прямыми \( \displaystyle AS\) и \( \displaystyle CE\).

Решение:

Из-за того, что в правильной пирамиде вершина при проекции попадает в центр основания, оказывается, что прямая \( \displaystyle AD\) — проекция прямой \( \displaystyle AS\).

Но мы знаем, что в правильном шестиугольнике \( \displaystyle AD\bot CE\). Применяем теорему о трёх перпендикулярах:

\( \displaystyle AD\bot CE\Rightarrow AS\bot CE\)

И пишем ответ: \( \displaystyle 90<>^\circ \).

Наши курсы по подготовке к ЕГЭ по математике, информатике и физике

К ЕГЭ можно подготовиться абсолютно бесплатно. У нас на сайте полно качественных материалов. Но вы должны знать что вы делаете.

Если у вас с этим сложности, приходите к нам.

И если вам нужен действительно высокий балл, приходите на наши курсы:

Мы качественно готовим к ЕГЭ даже тех, у кого «нет способностей».

Ну, рассказывай! 🙂

Мы будем очень рады услышать твое мнение об этой статье. Ведь эта тема сложная, хоть и короткая. И ты большой молодец.

Расскажи нам в комментариях ниже, помогла ли она тебе. Разобрался ли ты с теоремой о трех перпендикулярах?

Ты можешь задать нам любой вопрос. И мы обязательно ответим на него!

Добавить комментарий Отменить ответ

2 комментария

Очень грамотно и просто изложен материал. Рекомендую для повторения.

Источник

Перпендикулярные прямые — основные свойства, признаки и правила построения

В геометрии распространено понятие прямых. Они обозначаются двумя большими латинскими буквами или одной маленькой. При построении линии могут пересекаться и иметь только одну общую точку. Взаимно перпендикулярные прямые находятся относительно друг друга под углом 90°. Построение проводится при применении специальных инструментов.

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.