какие две прямые называют параллельными
Прямая линия. Параллельные прямые. Основные понятия.
Две прямые называются параллельными, если, находясь в одной плоскости, они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || СE
Возможность существования таких прямых доказывается теоремой.
Теорема.
Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой.
Пусть AB данная прямая и С какая-нибудь точка, взятая вне ее. Требуется доказать, что через С можно провести прямую, параллельную AB. Опустим на AB из точки С перпендикуляр СD и затем проведем СE ^ СD, что возможно. Прямая CE параллельна AB.
Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M. Тогда из точки M к прямой СD мы имели бы два различных перпендикуляра MD и MС, что невозможно. Значит, CE не может пересечься с AB, т.е. СE параллельна AB.
Следствие.
Аксиома параллельных линий.
Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.
Так, если прямая СD, проведенная через точку С параллельна прямой AB, то всякая другая прямая СE, проведенная через ту же точку С, не может быть параллельна AB, т.е. она при продолжении пересечется с AB.
Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).
Следствия.
1. Если прямая (СE) пересекается с одной из параллельных (СВ), то она пересекается и с другой (AB), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB, что невозможно.
2. Если каждая из двух прямых (A и B) параллельны одной и той же третьей прямой (С), то они параллельны между собой.
Действительно, если предположить, что A и B пересекаются в некоторой точке M, то тогда через эту точку проходили бы две различные прямые, параллельные С, что невозможно.
Теорема.
Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной.
Перпендикуляр EF, пересекаясь с AB, непременно пересечет и СD. Пусть точка пересечения будет H.
Предположим теперь, что СD не перпендикулярна к EH. Тогда какая-нибудь другая прямая, например HK, будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB: одна СD, по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH.
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.
Параллельные отрезки – два отрезка называются параллельными, если они лежат на параллельных прямых.
Параллельные лучи – два луча называются параллельными, если они лежат на параллельных прямых.
Теоретический материал для самостоятельного изучения.
Вы уже знаете, что на плоскости бывают пересекающиеся и непересекающиеся прямые, вы знаете, как их строить на чертеже. Теперь давайте рассмотрим прямые, которые называются параллельными, и научимся их строить различными способами.
Для начала дадим определение параллельным прямым.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Параллельные прямые имеют своё обозначение: a ║ b.
Рассмотрим прямые а и b, перпендикулярные прямой c. Ранее мы выяснили, что такие прямые не пересекаются, следовательно, прямые а и b параллельны.
Очень часто рассматриваются не только параллельные прямые, но и параллельные отрезки.
Дадим им определение.
Два отрезка называются параллельными, если они лежат на параллельных прямых.
Два луча называются параллельными, если они лежат на параллельных прямых.
Рассмотрим прямую с, пересекающую прямые а и b.
Прямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них.
Как видно из рисунка, при пересечении прямых а и b секущей c образуются 8 углов. Пронумеруем полученные углы.
Оказывается, некоторые пары образованных углов имеют свои названия.
Так, например, углы 3 и 5, 4 и 6 ‑ называются накрест лежащие углы.
Углы 4 и 5 или 3 и 6 ‑ называются односторонними углами.
А пары углов 1 и 5, 4 и 8, 2 и 6 или 3 и 7 ‑ называются соответственными углами.
Как же можно построить параллельные прямые?
Для построения параллельных прямых существует несколько способов построения с помощью различных чертёжных инструментов. Рассмотрим построение параллельных прямых с помощью чертёжного угольника и линейки.
Построим прямую b, проходящую через точку M и параллельную данной прямой а.
Приложим чертёжный угольник к прямой а, к нему приложим линейку. Теперь передвинем угольник вдоль линейки так, чтобы точка M оказалась на стороне угольника, остается провести прямую b. Прямые а и b будут параллельны, на основе признаков параллельности двух прямых, которые будут изучены позднее.
Материал для углублённого изучения темы
Другие способы построения параллельных прямых.
Рассмотрим ещё два способа построения параллельных прямых с помощью чертёжных инструментов.
В чертёжной практике очень часто используется способ построения параллельных прямых с помощью рейсшины.
При выполнении столярных работ, для разметки параллельных прямых используется ещё один инструмент – малка, который представляет собой две планки, скреплённые шарниром.
При нанесении параллельных рисок можно использовать рейсмус, который представляет собой деревянную заготовку с двумя регулируемыми брусками, на концах который прикреплены для нанесения рисок иглы или гвозди.
Разбор заданий тренировочного модуля
№ 1. Один из односторонних углов при двух параллельных прямых и секущей на 40º меньше другого. Найдите меньший угол, если известно, что сумма односторонних углов равна 180°.
Пусть х – меньший из односторонних углов, тогда больший равен х + 40. Т. к. сумма односторонних углов по условию равна 180°, составим уравнение.
х = 70° – градусная мера меньшего угла.
№ 2. Через параллельные прямые а и m проведены секущие АК и КР так, как показано на рисунке. КО = ВК = АК, при этом АК = КР = 9 см, отрезок ВО =АР, АР = 6 см. На сколько сантиметров периметр ∆ВОК меньше периметра ∆АКР?
Решение: найдём периметр ∆АКР.
Р∆АКР = АК + КР + АР = 9 + 9 + 6 = 24 см
Найдём периметр ∆КВО. Для этого вычислим длины сторон треугольника КВО, исходя из условия задачи.
КО = ВК =АК = 9 = 6 см.
Р∆КВО = ВК + КО + ВО = 6 + 6 + 4 = 16 см
Вычислим, на сколько периметр ∆ВОК меньше периметра ∆АКР.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №4. Параллельность прямых, прямой и плоскости
Перечень вопросов, рассматриваемых в теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.
Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.
Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.
Теоретический материал для самостоятельного изучения
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.
Существует еще два утверждения, которые используются при решении задач:
Примеры и разбор решения заданий тренировочного модуля
Тип задания: Ввод с клавиатуры пропущенных элементов в тексте
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.
Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10
Т.к. ACFE − параллелограмм, то АС=EF=10
Тип задания: Единичный / множественный выбор
Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.
MC
Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

Геометрия. 10 класс
Параллельность прямых, прямой и плоскости
Параллельность прямых, прямой и плоскости
Параллельность прямых, прямой и плоскости
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Лемма. Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Существует еще два утверждения, которые используют при решении задач:
1. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
2. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо тоже параллельна данной плоскости, либо лежит в этой плоскости.
Параллельные прямые, признаки и условия параллельности прямых
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
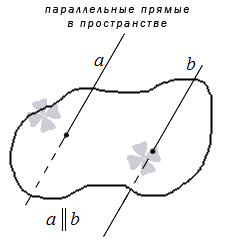
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
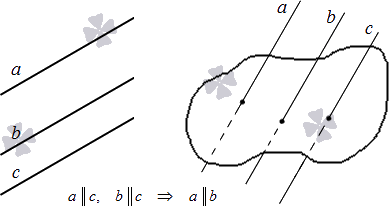
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
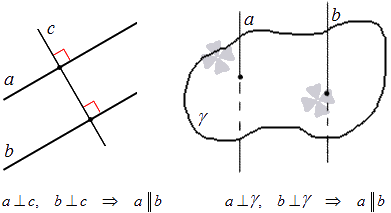
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
A 1 = t · A 2 B 1 = t · B 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
a x = t · b x a y = t · b y
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Решение
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Решение
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.