какие две буквы алфавита чаще всего используют в офисе

Как в Word сделать списки по алфавиту, автоматически?

Доброго всем времени суток!

Ворд является замечательным редактором. В котором можно не только писать тексты, но и форматировать их, практически. любым способом. Правда некоторые функции или очень трудоемки, или несовершенны. Но все-таки, вполне выполнимы.

Одна из таких функций – это создание списков и их сортировка. Если список небольшой и сортировка по алфавиту не нужна, то можно написать и так, или же самостоятельно расставить по алфавиту. А вот если список очень большой, и в нем много одинаковых первых букв? Впрочем, даже и небольшой список расставлять вручную по алфавиту достаточно долго, а хочется делать это быстро.

Как это сделать средствами ворд мы сейчас и рассмотрим.

Как в ворд сделать по алфавиту список из имен или фамилий?

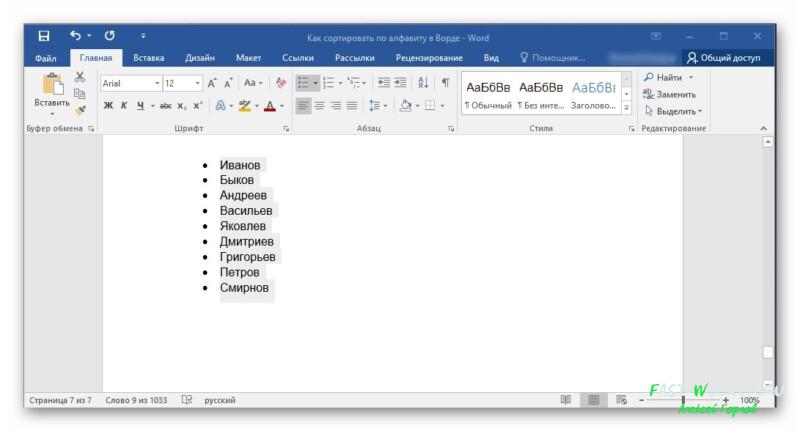
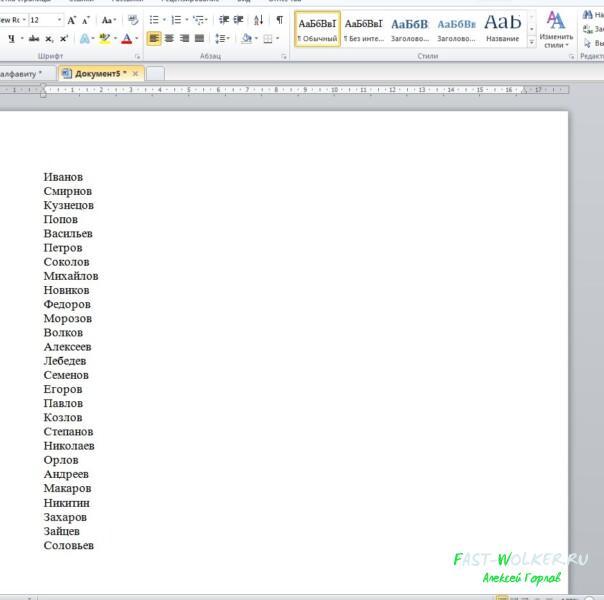
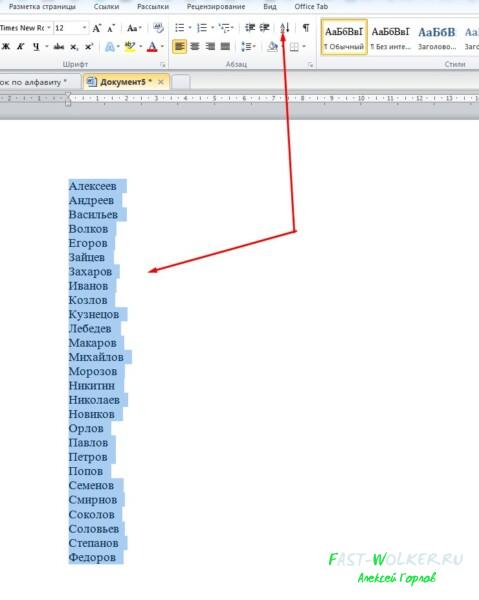
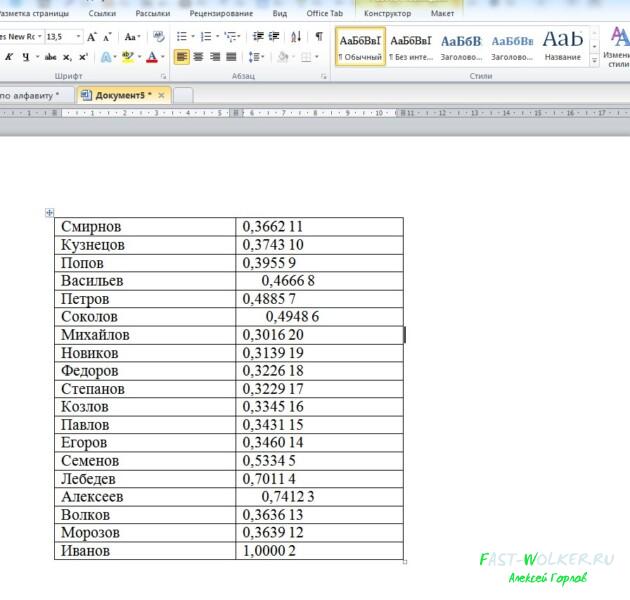
Итак, у нас имеется определенный список, скажем, фамилий.

Эти имена нам необходимо расставить в алфавитном порядке быстро и не прибегая к нудному перетаскиванию слов из одного ряда в другой.

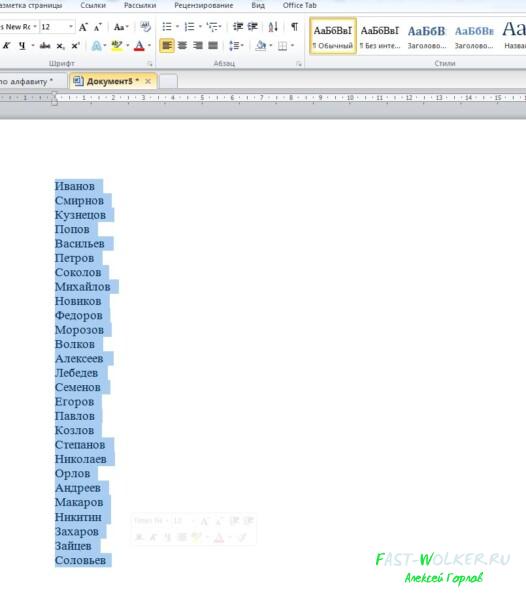
Первым делом выделяем мышкой все слова из списка.

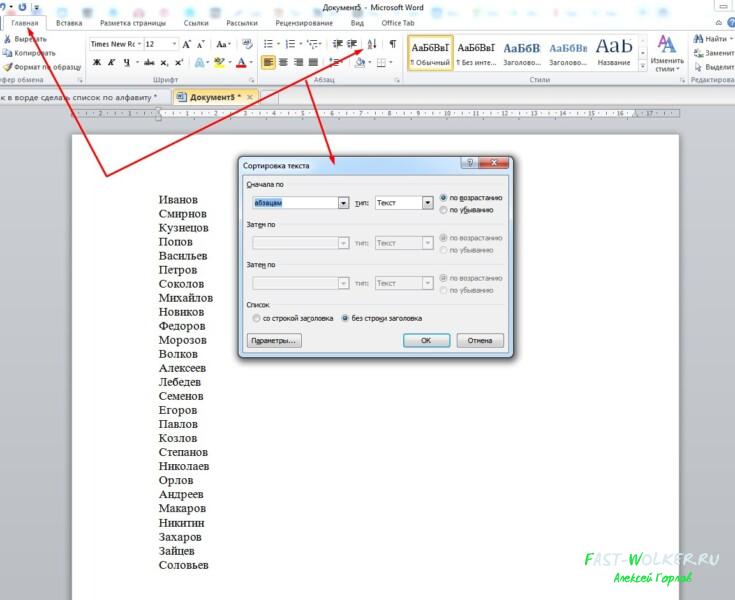
Затем во вкладке «Главная» идем в раздел «абзац», где находим кнопку со стрелкой и буквами А и Я. Нажимаем на эту кнопку. Откроется окно. Здесь в пункте «Сначала по» указываем «По абзацам», нажав на стрелку раскрывающегося меню, а в пункте «тип» рядом устанавливаем значение «текст».

Чаще всего эти значения уже стоят по умолчанию. И последнее, рядом ставим галочку как будем изменять список: по возрастанию, (т.е. по алфавиту), или по убыванию – в обратном порядке, соответственно.

Поскольку нам необходимо расположить фамилии в алфавитном порядке, ставим – по возрастанию. Далее жмем ОК. Все фамилии тут же перестроились в алфавитном порядке.

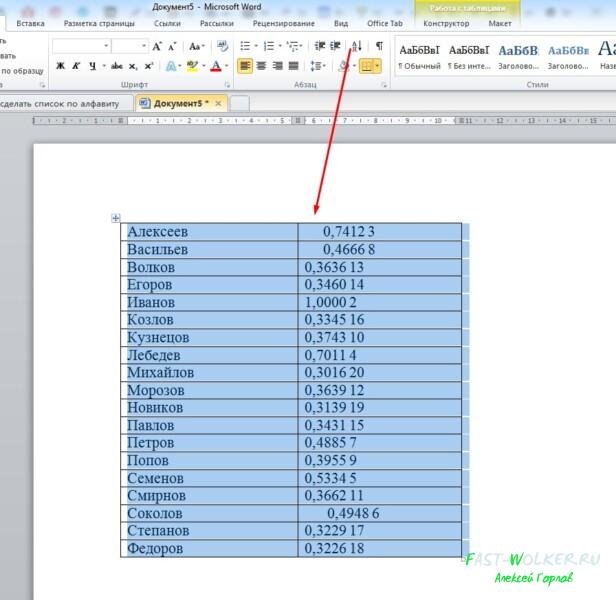
Часто бывает и так, что у нас имеется список фамилий, а рядом идут цифры, например дат рождения или зарплаты и пр. Здесь необходимо отсортировать не по алфавиту, а по убыванию цифр.

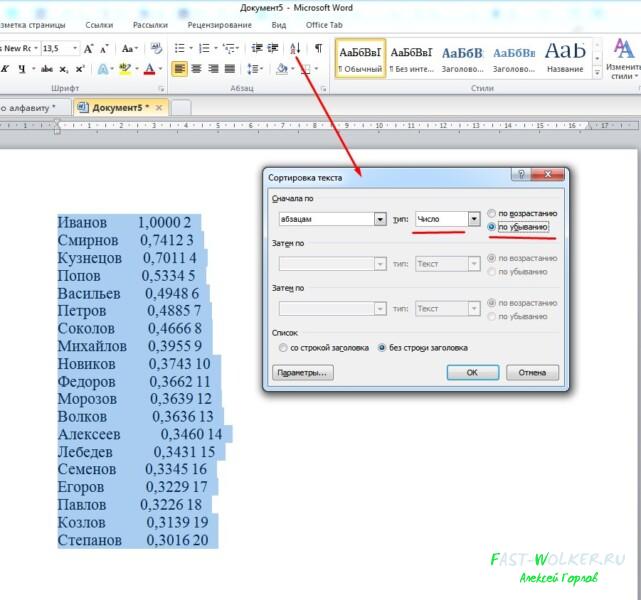
Здесь делаем все тоже, что и в первом пункте. Сначала выделяем текст, затем в разделе «абзац» выбираем кнопку со стрелкой и буквами А и Я. Затем, в открывшемся окне в пункте «Тип» ставим значение «Число», и выбираем «По убыванию».

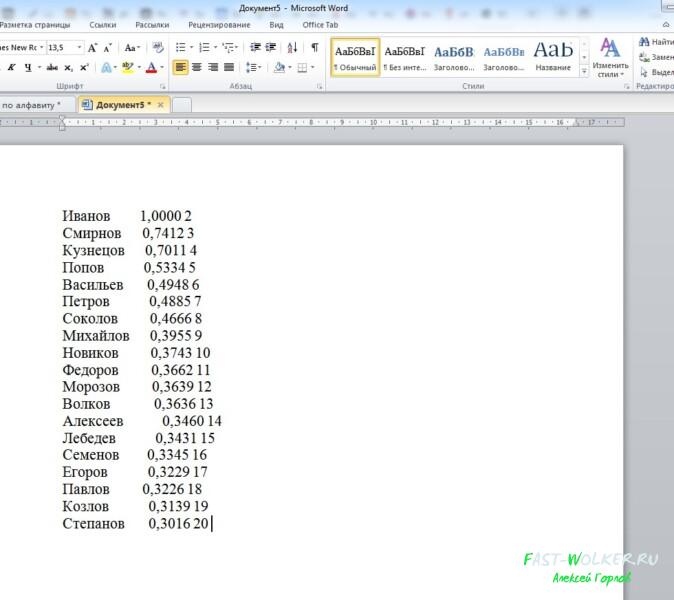
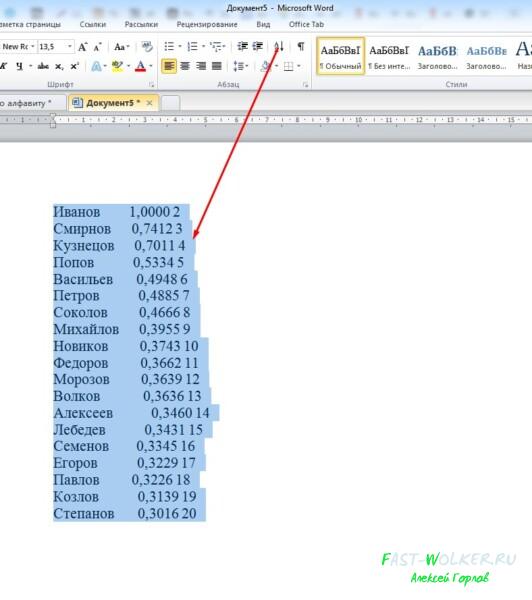
В результате у нас список будет выглядеть следующим образом

Фамилии оказались разбросаны, а вот цифровые значения расположились от самого большого, к самому малому. Кстати, в этой же строке «тип», когда откроете выпадающее меню, можно обнаружить и третье значение – «дата». Это значение ставится, когда вы сортируете список по датам.

Как отсортировать данные в таблице для списка в документе ворд?

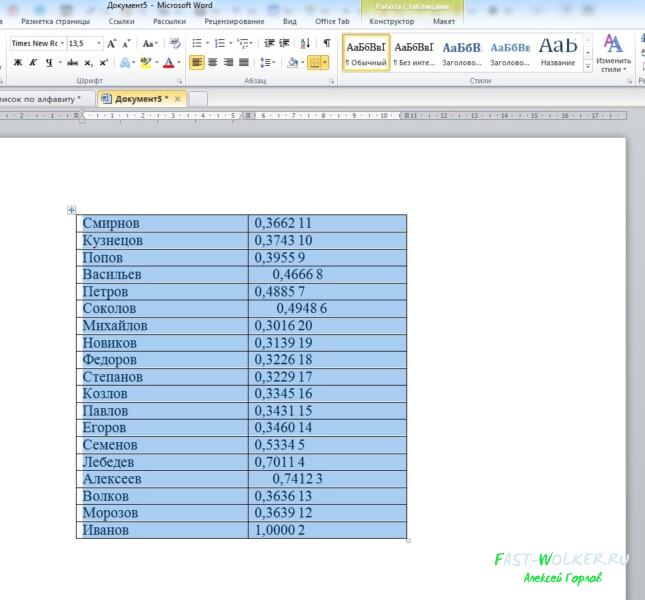
А теперь рассмотрим другой вариант. Все данные, которые у нас были представлены выше в тексте, теперь находятся в табличном формате.

Как быть в таком случае? Здесь все очень просто. Первым делом выделяем саму таблицу.

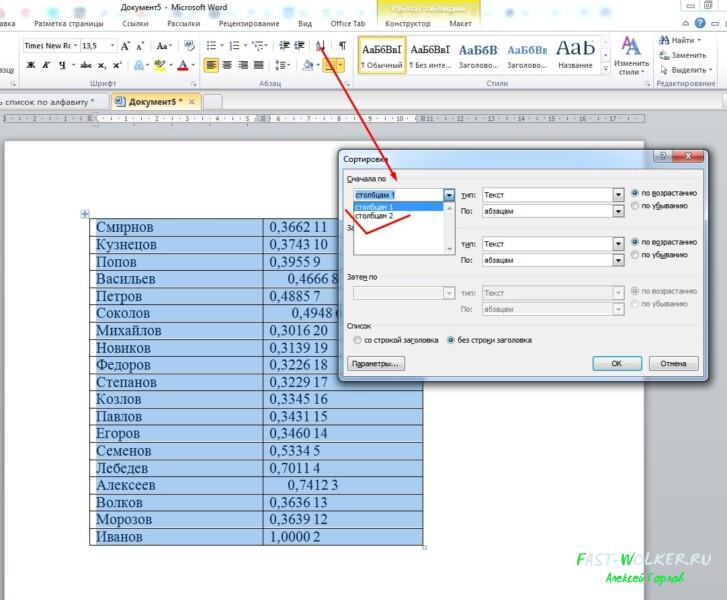
Затем так же, в разделе «абзац» нажимаем стрелку с буквами А и Я. Откроется окно, где в пункте «сначала по» увидим уже значения «столбцам 1» или «столбцам 2».

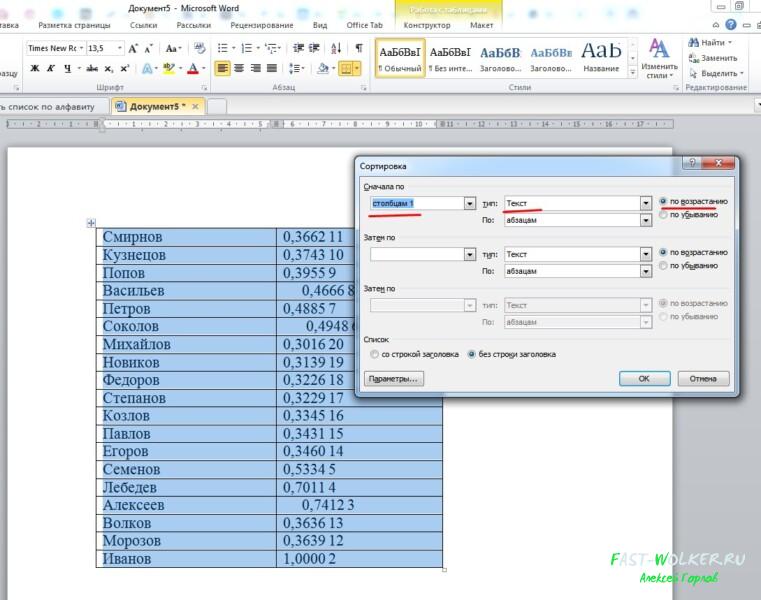
Впрочем, этих значений будет столько же, сколько столбцов в таблице. Как вы уже догадались, нам предлагают сортировку по разным столбцам. Выбираем по первому столбцу. Соответственно, «тип» указываем «текст» и галочку ставим «по возрастанию».

Установив все нужные значения, нажимаем ОК. В результате табличные данные у нас оформились фамилиями от А и до Я.

Если нам необходимо сортировать по цифрам, то выбираем второй столбец, а в поле «тип» указываем уже не «текст», а «число». Все здесь достаточно просто.

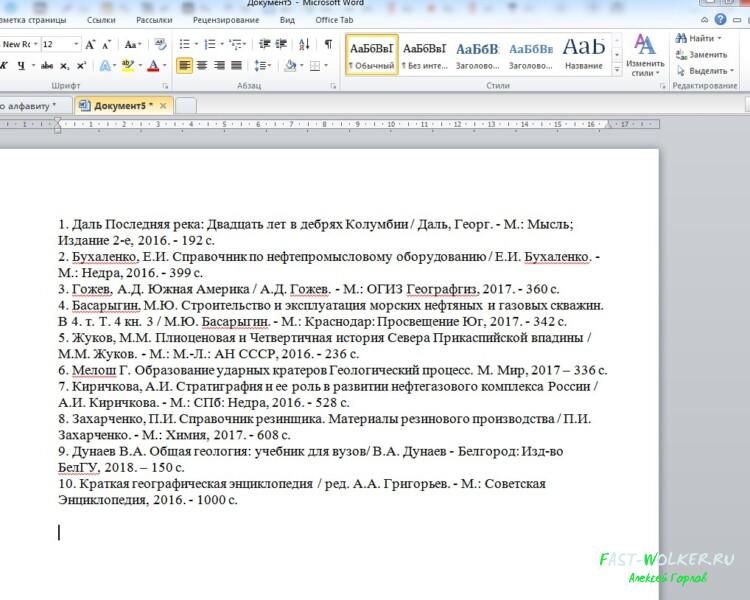
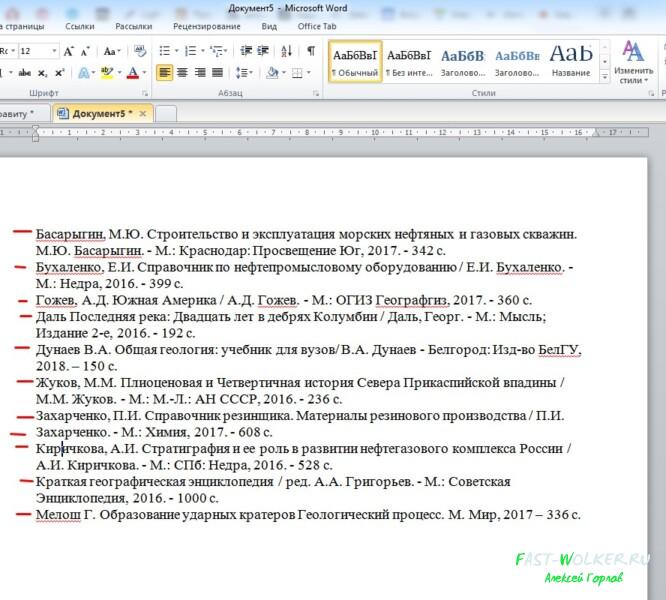
Следующий вариант, который актуален для тех, кто занимается рефератами, дипломами и прочими работами, где требуется приводить в конце список литературы.

Хорошо, что он состоит из трех наименований и вписать их в алфавитном порядке не составит труда. Но если вы его писали по мере нахождения авторов, то у вас получится список приведенным в разброс.

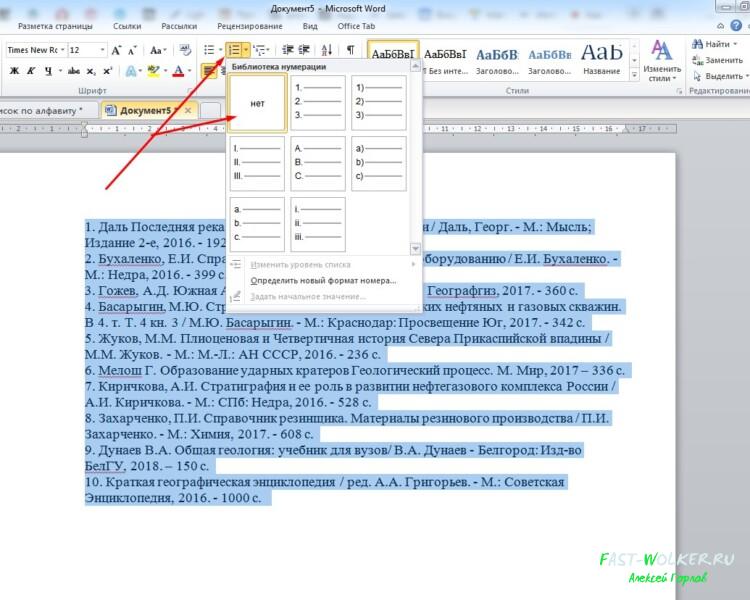
Если вы его составляли уже с нумерацией, то ее необходимо убрать, поэтому лучше писать список без цифр. Чтобы убрать нумерацию, выделяем наш список и идем в пункт «нумерация«, где в выпадающем меню выбираем категорию НЕТ.

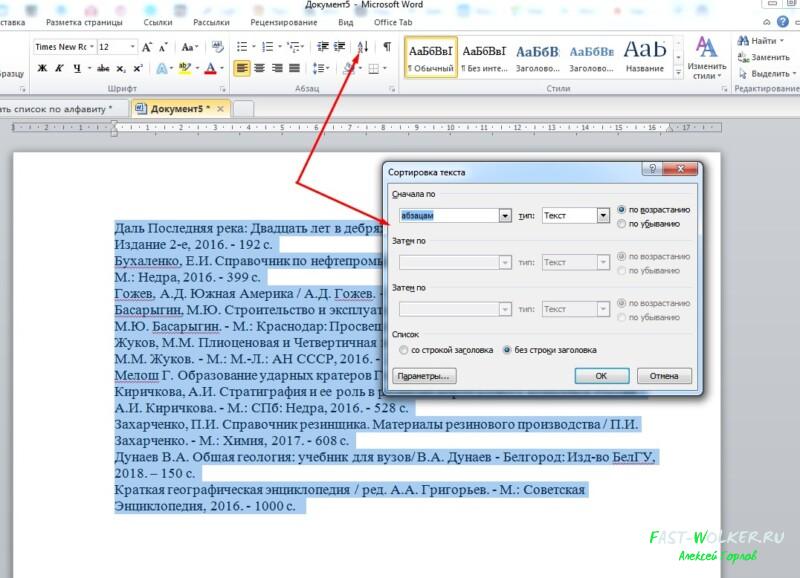
Теперь расставляем этот список по алфавиту. Для этого делаем все те же операции, которые описывались выше. Выбираем в разделе «абзац» кнопку сортировки и, в открывшемся окне выставляем значения по абзацам, текст и «по возрастанию«.

Установив нужные значения, жмем ОК. В результате список литературы встал по алфавиту.

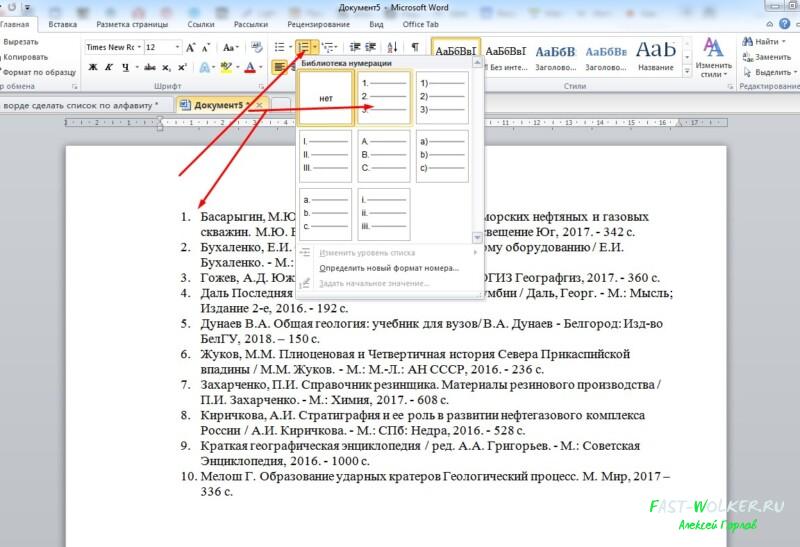
Остается только его пронумеровать для порядка. Выделяем список, идем в пункт нумерация и ставим там тот вариант, который требует ГОСТ. Жмем ОК и список литературы стал у нас пронумерованным.

Вот так легко и быстро можно расставить по алфавиту или по возрастанию и убыванию данные текста или цифровых значений. Успехов!

Источник

Информатика 7 класс Тема: Знаки
Дам 50 баллов если поможите в тесте.
Вопрос № 1
Укажите разновидности визуальных знаков?
Выберите несколько из 4 вариантов ответа:

Пиктограммы
Фонемы
Слоги
Символы
Вопрос № 2
Как называется знаковая система, которую человек использует для выражения своих мыслей и для общения с другими людьми?

Алфавит
Язык
Фонемы
Цифры
Вопрос № 3
Как называются визуальные знаки, имеющие явное соглашение об использовании и представляющие собой упрощённое изображение объекта-оригинала?

Пиктограммы
Символы
Буквы
Цифры
Вопрос № 4
Знаки каких типов используются людьми для общения?
Выберите несколько из 5 вариантов ответа:

Визуальные
Обонятельные
Звуковые
Вкусовые
Тактильные
Вопрос № 5
Установите соответствие между знаками и их формами.
Укажите соответствие для всех 4 вариантов ответа:
1) Метки территории у животных __ Визуальный
2) Азбука Брайля __ Обонятельный
3) Рисунок __ Звуковой
4) Звонок будильника __ Тактильный

1234
3421
3142
Вопрос № 6
Какое минимальное количество знаков может содержать знаковая система?
Запишите число:

Введите ответ:
Вопрос № 7
Как называются звуковые знаки языка?
Составьте слово из букв:
МФОНЕЫ

Введите ответ:
Вопрос № 8
Как называется некоторый заменитель объекта, свойства, явления или отношения, используемый для передачи информации?

Знак
Цифра
Пиктограмма
Символ
Вопрос № 9
Какие виды письменности существуют?
Выберите несколько из 5 вариантов ответа:

Буквенно-звуковая
Идеографическая
Словесная
Фразовая
Слоговая
Вопрос № 10
Как называется знаковая система, которую человек использует для выражения своих мыслей и для общения с другими людьми?

Источник

Решения задач по комбинаторике

Решения задач по комбинаторике

I. На использование принципов умножения и сложения

1. Сколькими способами могут восемь человек стать в очередь к театральной кассе?

Существует 8 мест, которые должны занять 8 человек. На первое место может стать любой из 8 человек, т. е. способов занять первое место – 8. После того, как один человек стал на первое место, осталось 7 мест и 7 человек, которые могут быть на них размещены, т. е. способов занять второе место – семь. Аналогично для третьего, четвертого и т. д. места. Используя принцип умножения, получаем произведение – . Такое произведение обозначается как 8! (читается 8 факториал) и называется перестановкой P8.

2. Позывные радиостанции должны начинаться с буквы W. 1) Скольким радиостанциям можно присвоить различные позывные, если позывные состоят из трех букв, причем эти буквы могут повторяться? 2) Если позывные состоят из четырех букв, которые не повторяются?

В современном латинском алфавите 26 букв. На первом месте всегда должна стоять одна буква, следовательно, существует только один способ занять первое место.

1) На оставшиеся два места может претендовать любая из 26-ти букв, т. к. буквы в позывных могут повторяться. Используя принцип умножения, получаем произведение: 1= 262.

2) На второе место можно поставить любую из 25 букв, т. к. в позывных буквы не должны повторяться. На третье место – 24 буквы, на четвертое место – 23 буквы. Используя принцип умножения, получаем произведение: 1.

Ответ:; 2) .

3. В автомашине 7 мест. Сколькими способами семь человек могут усесться в эту машину, если занять место водителя могут только трое из них?

Действие, которое должно быть выполнено особым способом, необходимо выполнять первым. Итак, на место водителя можно посадить только одного из трех человек (умеющего водить машину), т. е. существуют 3 способа занять первое место. Второе место может занять любой из 6 человек, оставшихся после того, как место водителя будет занято. И т. д. Используя принцип умножения, получаем произведение: 3 = 36! = 3P6.

Ответ: 3P6 = 36!.

4. Алфавит некоторого языка содержит 30 букв. Сколько существует шестибуквенных слов (цепочка букв от пробела до пробела), составленных из букв этого алфавита, если:

1) буквы в словах не повторяются?

2) буквы в словах могут повторяться?

Существует шесть мест, на которые нужно разместить 30 букв.

1. Буквы не должны повторяться. Используя принцип умножения, получаем произведение: . Такое произведение достаточно сложно использовать в дальнейшем, и информация задачи представлена в ней в скрытой форме. В комбинаторике используют для таких произведений формулу размещений. Чтобы получить формулу размещений, умножим это произведение на единицу, которую представим следующим образом: 1 = = = = = А ‑ формула для размещений.

2. Буквы повторяются. Используя принцип умножения, получаем: 303030303030 = 306 = Ã – формула для размещений с повторениями.

Ответ: 1) А; 2) Ã.

5. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых содержит не менее трех цифр. Сколько таких чисел можно составить, если повторения цифр в числах запрещены?

II. На использование формул для перестановок и размещений

1. Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять:

(а) из восьми букв, (б) из семи букв, (в) из трех букв?

В слове фрагмент 8 букв алфавита.

(а) Всевозможные перестановки 8 букв по восьми местам: А = =P8.

(б) Размещения 8 букв по 7 местам: А.

(в) Размещения 8 букв по 3 местам: А.

2. Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, а) если первая из них не равна нулю; б) если номер состоит из одной буквы латинского алфавита, за которой следуют четыре цифры, отличные от нуля?

а) Всего существует 10 цифр. На первом месте не может быть цифры 0, поэтому способов поставить цифру на первое место существует 9. На втором месте может стоять любая из 10-ти цифр (цифры могут повторяться), т. е. способов поставить цифру на второе место существует 10, и т. д. Используя принцип умножения, получаем: 910101010 = 9104 =9Ã.

Ответ: 9Ã, 26Ã.

3. Сколькими способами можно расставить на полке семь книг, если (а) две определенные книги должны всегда стоять рядом, (б) эти две книги не должны стоять рядом?

(а) Книги, которые должны стоять рядом, считаем за одну книгу. Тогда нужно расставить 6 книг по шести местам. Применяя формулу перестановок, получаем: P6 = 6!. Мы учли перестановки шести книг, не учитывая порядок внутри тех книг, которые мы посчитали за одну. А так как две книги по двум местам можно разместить только двумя способами (P2), то получаем окончательно следующее произведение: P2P6 =2 6! = 1440.

(б) Способов переставить 7 книг существует P7= 7!. Из них ‑ 26! способов поставить определенные книги вместе. Следовательно, способов поставить книги так, чтобы 2 заданные книги не стояли вместе существует: 7! ‑ 26!.

III. На использование формул для сочетаний

1. Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

Для решения этой задачи необходимо использовать формулу для сочетания элементов, т. к. здесь не имеет значения порядок элементов в выборке. Запишем формулу для сочетаний и произведем вычисления:

С = .

2. Компания из двадцати мужчин разделяется на три группы, в первую из которых входят три человека, во вторую — пять и в третью — двенадцать. Сколькими способами они могут это сделать? (Ответ записать в виде произведения сомножителей, не вычисляя его.)

Ответ: С С С.

3. Сколькими способами можно отобрать несколько фруктов из семи яблок, четырех лимонов и девяти апельсинов? (Мы считаем, что фрукты одного вида неразличимы.)

Т. к. фрукты одного вида неразличимы, то существует один способ взять одно яблоко, один способ взять 2 яблока, один способ взять три яблока и т. д., т. е. всего семь способов выбрать несколько яблок (несколько – это не менее одного). Необходимо также прибавить один способ не взять ни одного яблока. Следовательно, существует 8 способов взять яблоки. Аналогично существует 5 способов выбрать лимоны и 10 способов выбрать апельсины. Следуя принципу умножения, получим все способы отбора фруктов: 7510. Но среди этих способов существует один способ, когда не выбирается ни один фрукт. Следовательно, решением данной задачи будет следующее выражение: 7510 – 1 = 349.

IV. На использование формул для перестановок и сочетаний

1. Сколько четырехбуквенных слов можно образовать из букв слова сапфир? 2) Сколько среди них таких, которые не содержат буквы р? 3) Сколько таких, которые начинаются с буквы с и оканчиваются буквой р?

1. Из шести букв составляются четырехбуквенные слова, причем порядок букв важен для образования новых слов. Поэтому используется формула для размещений: А.

2. Необходимо исключить букву р из рассмотрения. Количество слов, не содержащих эту букву: А.

3. На первое место поставить букву с можно только одним способом. На последнее место поставить букву р можно тоже только одним способом. Остаются 4 буквы, которые необходимо разместить по двум местам: А.

2. Сколько пятибуквенных слов, каждое из которых состоит из трех согласных и двух гласных, можно. образовать из букв слова уравнение?

В слове уравнение 3 согласных и 4 гласных буквы русского алфавита. Чтобы посчитать количество требуемых пятибуквенных слов, необходимо посчитать количество сочетаний 3 согласных из 3-х заданных и двух гласных из четырех заданных: С и С. После того, как 5 букв выбраны, необходимо посчитать все возможные перестановки этих букв: С С P5.

Ответ: СС P5.

V. На использование формул для перестановок и сочетаний с повторениям

1. Сколько различных перестановок можно образовать изо всех букв слова перестановка? Сколько из них начинается с буквы п и оканчивается буквой а?

В слове перестановка 12 букв, из них повторяются 2 буквы е и две буквы а. Число перестановок из 12 элементов вычисляется с помощью формулы P12. Но среди этих перестановок будут повторяющиеся, в которых буквы е или а меняются местами. Чтобы не считать такие перестановки, используется формула для перестановок с повторениями: = .

Чтобы посчитать количество перестановок, начинающихся на букву п и оканчивающихся на букву а, необходимо исключить эти элементы и места, на которых они стоят из рассмотрения. Остается 10 букв и десять мест, причем остается только одна повторяющаяся буква е. Применяем формулу для перестановок с повторениями:

= .

Ответ: , .

Источник