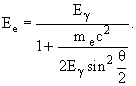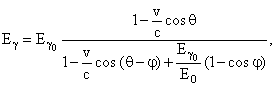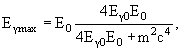какие длины волн электромагнитного излучения характерны для фотоэффекта эффекта комптона

Эффект Комптона

Как мы знаем, Альберт Эйнштейн в 1905 году предложил для объяснения фотоэффекта так называемую концепцию фотонов. Позже, в 1922 г., американский физик А.Комптон провел серию опытов и подтвердил ее экспериментально. Он провел исследования упругого рассеяния коротковолнового рентгеновского излучения на свободных электронах вещества (или электронах, слабо связанных с атомами) и открыл, что длина волны рассеянного изучения не соответствует ранее принятой волновой теории. Согласно ей, электроны, испытывающие воздействие периодического поля световой волны, совершают вынужденные колебания на частоте волны и поэтому излучают рассеянные волны той же частоты, следовательно, длина волны излучения при рассеянии не должна меняться.

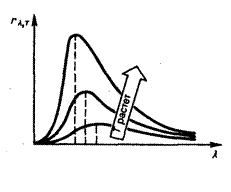
Соотношение интенсивности обеих линий связано с тем, какое вещество использовано в качестве рассеивающего.

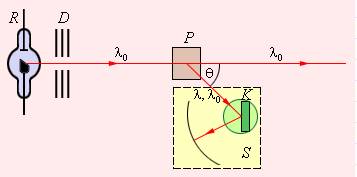
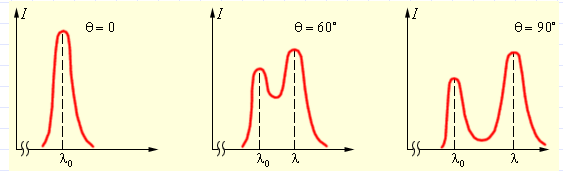
Следующие иллюстрации показывают, как распределяется интенсивность в спектре рассеянного излучения в зависимости от угла рассеивания.

Объяснение эффекта с помощью квантовых представлений

Эффект Комптона был объяснен в 1923 году самим Комптоном и П. Дебаем, которые работали независимо друг от друга. В обоих случаях в основе объяснения лежат квантовые представления.

Если излучение является потоком фотонов, то эффект Комптона происходит из-за упругого столкновения свободных электронов вещества с рентгеновскими фотонами. Рассеивающие вещества имеют слабую связь между ядрами атомов и электронами, поэтому можно считать, что они имеют в составе свободные электроны. При столкновении им передается часть энергии фотонов и часть импульса.

Также нам понадобится закон сохранения импульса:

С помощью теоремы косинусов мы можем перевести его в скалярную форму:

Почему длина части волн не изменяется?

Согласно данным опыта, в излучении после рассеяния кроме смещенной линии есть и несмещенная, длина волны излучения которой совпадает с первоначальной. Ее наличие можно объяснить тем, что часть фотонов взаимодействует с электронами, крепко связанными с ядрами атомов. Тогда происходит обмен энергии и импульса с атомом в целом, а не только с электроном. Поскольку атом весит значительно больше, то переданная энергия фотона очень мала, следовательно, длина волны λ рассеянного излучения остается практически неизменной.

Источник

Тема 13. Корпускулярная оптика. Фотоэффект и эффект Комптона

Соглас­но квантовой гипотезе Планка-Эйнштейна свет частотой n испускается, распространяется и поглощается веществом отдельными порциями (квантами), энергия которых e_о=hn (h – постоянная Планка). Эти локализованные в пространстве дискретные световые кванты, движущиеся со скоростью с рас­пространения света в вакууме, получили назва­ние фотонов. Таким образом, распространение света можно рассматривать не как непрерывный волновой процесс, а как поток частиц – фотонов. Доказательством этих квантовых (корпускулярных) представлений о свете, как о потоке частиц, являются фотоэффект и эффект Комптона.

Внешним фотоэффектом называется испускание электронов веществом под действием электромагнитного излучения. Явление внешнего фотоэффекта и его закономерности объяснены на основе квантовой теории фотоэффекта, согласно которой каждый квант света поглощается только одним электроном.

Энергия hn падающего на металл фотона расходуется на совершение электроном работы вы­хода А из металла и на сообщение вылетевшему фотоэлектрону кинетичес­кой энергии, то есть по закону сохранения энергии:

(уравнение Эйнштейна для внешнего фотоэффекта).

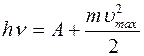
Из этого уравнения следует, что максимальная кинетическая энергия фотоэлектрона ли­нейно возрастает с увеличением частоты падающего излучения и не зависит от его интенсивности, то есть от числа фотонов. Так как с уменьшением частоты света кинетическая энергия фотоэлектронов уменьшается, то при некоторой частоте n=n₀ кинетическая энергия фотоэлектронов станет равной нулю и в том случае энергия фотона hn₀ равна работе выхода А, из чего следует, что n₀=А/h (частота n₀ носит название красной границы фотоэффекта). При частоте n 2 следует, что масса фотона:

.

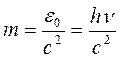
Фотон движется со скоро­стью света с, поэтому импульс р фотона:

.

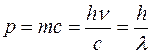
Полученные выражения связывают корпускулярные характеристики фотона – массу, импульс и энергию – с волновой характеристикой света – его частотой n (или его длиной волны l).

Корпускулярные свойства света проявляются в эффекте Компто­на.

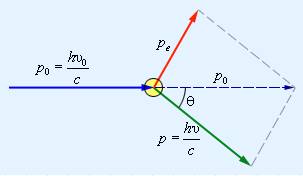
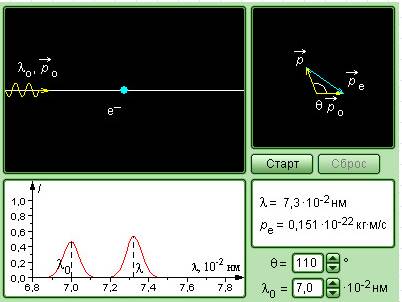
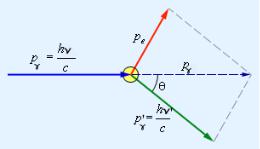
Эффектом Комптона называется увеличение длины волны коротковолнового электромаг­нитного излучения при его упругом рассеянии на свободных электронах вещества. Опыты Комптона показали, что разность длин волн рассеянного (l’) и падающего (l) электромаг­нитного излучения, то есть величина Dl=l’–l не зависит от длины волны l падающего излучения и природы рассеивающего вещества (РВ), а определяется только углом рассея­ния q, то есть углом между направлениями лучей до и после рассеяния (рис. 29):

, где–комптоновская длина волны.

Эффект Комптона не укладывается в рамки волновой теории света, и его объяснение дано на основе квантовых представлений о природе света. Если рассматривать излучение, как поток фотонов, то эффект Комп­тона – это результат упругого столкновения рентгеновских фотонов со свободными элек­тронами рассеивающего вещества. В процессе этого столкновения фотон переда­ет электрону часть своей энергии, что ведет к увеличению длины волны при рассеянии фотона.

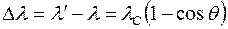
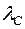
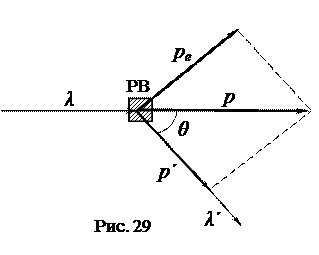
(На рисунке 29 введены следующие обозначения: p и p’ – импульсы фотона до и после рассеяния; p_e – импульс электрона после рассеяния на нем фотона).

Исходя из законов сохранения импульса и энергии

для упругого столкновения двух частиц (рис. 29) – налетающего фотона с покоящимся свободным электро­ном вещества, было получено следующее выражение для величины Dl:

, где пм.

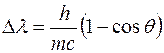
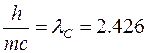
Это выражение для величины Dl, полученное на основе корпускулярных представлений о свете, оказалось аналогично приведенному выше выражению для величины Dl, полученному Комптоном экспериментально.

Следовательно, эффект Комптона является экспериментальным доказательст-вом проявления корпускулярных свойств света как потока частиц – фотонов. Итак, рассмотренные явления фотоэффекта и эффекта Комптона служат доказательством квантовых (корпускулярных) представлений о свете как о потоке фотонов, а, с другой стороны, такие явления, как интерференция, дифракция и поляризация света подтверждают волновую природу света. Таким образом, свет, обладая одновременно корпускулярными и волновыми свойствами, проявляет так называемый корпускулярно-волновой дуализм.

Тема 14. Тепловое излучение

Излучение света телами, обусловлен­ное их нагреванием, называется тепловым излучением. Количественно тепловое излучение характеризуется спектраль-ной плот­ностью энергетической светимости тела,т.е. мощностью излучения с еди­ницы площади поверхности тела в интервале частот единичной ширины:

, где

.

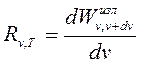
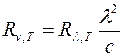
Зная спектральную плотность энергетической светимости, можно вычислить интег­ральную энергетическую светимостьR_T :

.

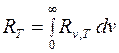
Способность тел поглощать падающее на них излучение характеризуется спект­ральной поглощательной способностью А_n,T :

,

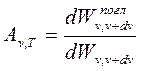
Тело, способное поглощать полностью при любой температуре всё падающее на него излучение любой частоты, называется черным телом. Следовательно, спектральная поглощательная способность черного тела для всех частот и температур тождественно равна единице ().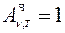

Закон Кирхгофа. Кирхгоф установил, что отношение спектральной плотности энергетической светимости R_n,T к спектральной поглощательной способности А_n,T не зависит от природы тела; оно является для всех тел универсальной функцией r_n,T частоты n (или длины волны l) и температуры Т:

.

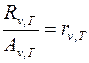
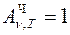
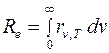
Для черного тела , поэтому из закона Кирхгофа вытекает, что универсальная функция Кирхгофа r_n,T – это спектральная плотность энергетической светимости R_n,T черного тела. Тогда выражение для интег­ральной энергетической светимости черного тела R_e можно записать в виде:

.

Энергетическая светимость черного тела R_e зависит только от температуры.

Закон Стефана – Больцмана. Согласно закону Стефана – Больцманаэнергетическая светимость черного тела R_e зависит от температуры Т следующим образом: 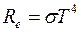, где s – постоянная Стефана – Больцмана.

Закон смещения Вина. Из эксперимен­тальных кривых зависимости функции r_l,T от длины волны l при различных температурах (рис. 30) следует, что распределение энергии в спектре черного тела является неравномерным. Все кривые имеют ярко выраженный максимум, который по мере повышения температуры смещается в сторону более коротких волн.

Источник

Какие длины волн электромагнитного излучения характерны для фотоэффекта эффекта комптона

Эффект Комптона
_{Compton effect}

,

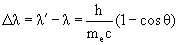
где θ – угол рассеяния фотона, а m_e – масса электрона h/m_ec = 0.024 Å называется комптоновской длиной волны электрона.
Изменение длины волны при комптоновском рассеянии не зависит от λ и определяется лишь углом θ рассеяния γ-кванта. Кинетическая энергия электрона определяется соотношением

Эффективное сечение рассеяния γ-кванта на электроне не зависит от характеристик вещества поглотителя. Эффективное сечение этого же процесса, рассчитанное на один атом, пропорционально атомному номеру (или числу электронов в атоме) Z.
Сечение комптоновского рассеяния убывает с ростом энергии γ-кванта: σ_k

Обратный комптон-эффект

Если электрон, на котором рассеивается фотон, является ультрарелятивистским Ee >> E_γ, то при таком столкновении электрон теряет энергию, а фотон приобретает энергию. Такой процесс рассеяния используется для получения моноэнергетических пучков γ-квантов высокой энергии. С этой целью поток фотонов от лазера рассеивают на большие углы на пучке ускоренных электронов высокой энергии, выведенных из ускорителя. Такой источник γ-квантов высокой энергии и плотности называется Laser-Electron-Gamma-Source (LEGS). В работающем в настоящее время источнике LEGS лазерное излучение с длиной волны 351.1 мкм (

0.6 эВ) в результате рассеяния на электронах, ускоренных до энергий 3 ГэВ, превращается в поток γ-квантов с энергиями 400 МэВ).
Энергия рассеянного фотона E_γ зависит от скорости v ускоренного пучка электронов, энергии E_γ0 и угла столкновения θ фотонов лазерного излучения с пучком электронов, угла между φ направлениями движения первичного и рассеянного фотона

При «лобовом» столкновении

E₀ − полная энергия электрона до взаимодействия, mc 2 − энергия покоя электрона.
Если направление скоростей начальных фотонов изотропно, то средняя энергия рассеянных фотонов _γ определяется соотношением

_γ = (4E_γ/3)·(E_e/mc 2 ).

При рассеянии релятивистских электронов на микроволновом реликтовом излучении образуется изотропное рентгеновское космическое излучение с энергией
E_γ = 50–100 кэВ.
Эксперимент подтвердил предсказанное изменение длины волны фотона, что свидетельствовало в пользу корпускулярного представления о механизме эффекта Комптона. Эффект Комптона наряду с фотоэффектом явился убедительным доказательством правильности исходных положений квантовой теории о корпускулярно-волновой природе частиц микромира.

П o дробнее об обратном комптон-эффекте см. Источники гамма-излучения

Источник

Эффект Комптона

В первые десятилетия ХХ века ученые всё больше осознавали, что объекты микромира обладают одновременно свойствами и частиц, и волн (см. Принцип дополнительности). Начало этому процессу положило предложенное Альбертом Эйнштейном объяснение фотоэлектрического эффекта, согласно которому любое электромагнитное излучение, включая свет, представляет собой пучки фотонов. Открытый же американским физиком Артуром Комптоном эффект рассеяния фотонов на свободных электронах стал еще одним подтверждением квантовой природы фотона.

Эксперимент, проделанный Комптоном, описать несложно. Пучок электромагнитных лучей (Комптон использовал рентгеновские лучи) направляется на кристалл, после чего измеряются энергии и угол отклонения рассеянных лучей. В рамках классической теории взаимодействия лучей с веществом (до постулирования принципов квантовой механики) энергия отраженного излучения не должна отличаться от энергии исходного излучения. Комптон же получил принципиально иную картину: энергия рассеянной волны отличалась от энергии исходной волны, и эта разница зависела от угла рассеяния, достигая максимума при угле 90°. Единственным способом дать разумную интерпретацию полученным Комптоном результатам было рассматривать взаимодействие лучей с атомами как столкновение исходящей частицы (фотона) с электроном. Как и два бильярдных шара, эти две частицы, взаимодействуя, отскакивают друг от друга. А поскольку электрон движется медленно, он, в общем случае, должен приобретать энергию при этом столкновении, в то время как фотон эту же энергию теряет.

После публикации Комптоном в начале 1923 года полученных результатов среди физиков осталось мало сомневающихся в реальности фотонов. Сегодня эффект Комптона находит применение в астрофизике: гамма-лучи от космических объектов подвергаются многократному рассеянию, пока их энергия не падает до длин волн рентгеновской части спектра, после чего их можно анализировать на стандартных рентгенографических установках. Подобный детектор был в 1991 году выведен НАСА на орбиту в составе Гамма-лучевой обсерватории имени Комптона.

Американский физик. Родился в Вустере, штат Огайо (Wooster, Ohio), в семье профессора философии. В 1916 году окончил Принстонский университет. В первые годы после окончания университета работал в частной промышленной лаборатории, где участвовал в создании первых ламп дневного света. Вернувшись к академическим исследованиям, большую часть времени проработал в Чикагском университете, где в 1923 году стал профессором физики. За открытие и объяснение эффекта Комптона он был удостоен Нобелевской премии по физике за 1927 год. Во время Второй мировой войны Комптон руководил металлургической лабораторией при Чикагском университете, участвовавшей в работе по созданию «уранового котла» в рамках Манхэттенского проекта. После окончания Второй мировой войны Комптон много своего времени стал уделять общественно-политической деятельности. В частности, с 1946-го по 1948 год состоял членом Комиссии по высшему образованию при президенте США.

Источник

В.К. Иванов. Волновая оптика / КОНСПЕКТ (по экзаменационным вопросам) / 34_Эффект Комптона

Эффектом Комптона называется упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ-излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна: под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.

Объяснение эффекта Комптона дано на основе квантовых представлений о природе света. Если считать, как это делает квантовая теория, что излучение имеет корпускулярную природу, т. е. представляет собой поток фотонов, то э ффект Комптона

— результат упругого столкновения рентгеновских или γ- фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядрами атомов, поэтому их можно считать свободными). В процессе этого столкновения фотон передает электрону часть своих энергии и импульса в соответствии с законами их сохранения.

Рис. 1. Закон сохранения импульса при рассеянии фотона на свободном электроне

Рассмотрим упругое столкновение двух частиц (рис.1) — налетающего фотона,

энергия покоя которого

столкнувшись с электроном, передает ему часть своей энергии и импульса и изменяет направление движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. Пусть импульс и энергия рассеянного фотона равны

Электрон, ранее покоившийся, приобретает

приходит в движение — испытывает отдачу. При каждом таком столкновении выполняются законы сохранения энергии и импульса.

Подставив в выражении (3) значения величин и представив (4) используя теорему косинусов, в соответствии с рис. 1, получим

Перепишем равенство (5) в виде

и возведем его в квадрат

m 2 c 4 − m 2 υ 2 c 2 = m 2 0 c 4 + h 2 ν

2 + h 2 ν ′ 2 − 2 h 2 νν

Масса электрона отдачи связана с его скоростью соотношением

, или m 2 ( c 2 − υ 2 ) = m

Учитывая (9), на основании (8) запишем

− λ ) = m c (1 − cos θ ) = m c sin 2

Наличие в составе рассеянного излучения несмещенной линии (излучения первоначальной длины волны) можно объяснить следующим образом. При рассмотрении механизма рассеяния предполагалось, что фотон соударяется лишь со свободным электроном. Однако если электрон сильно связан с атомом, как это имеет место для внутренних электронов (особенно в тяжелых атомах), то фотон обменивается энергией и импульсом с атомом в целом. Так как масса атома по сравнению с массой электрона очень велика, то атому передается лишь ничтожная часть энергии фотона. Поэтому в данном случае длина волны рассеянного излучения практически не будет отличаться от длины волны падающего излучения.

Из приведенных рассуждений следует также, что эффект Комптона не может наблюдаться в видимой области спектра, поскольку энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным.

Эффект Комптона наблюдается не только на электронах, но и на других заряженных частицах, например протонах, однако из-за большой массы протона его отдача просматривается лишь при рассеянии фотонов очень высоких энергий. Как эффект Комптона, так и фотоэффект на основе квантовых представлений обусловлены взаимодействием фотонов с электронами. В первом случае фотон рассеивается, во втором

— поглощается. Рассеяние происходит при взаимодействии фотона со свободным электроном, а фотоэффект — со связанными электронами. Можно показать, что при

столкновении фотона со свободным электроном не может произойти поглощения фотона, так как это находится в противоречии с законами сохранения импульса и энергии. Поэтому при взаимодействии фотонов со свободными электронами может наблюдаться только их рассеяние, т. е. эффект Комптона.

На рис. 2 показаны экспериментальные результаты по наблюдению комптоновского рассеяния на мишени из графита, имеющего электрон, слабо связанный с ядром атома. С увеличением угла θ все более отчетливо проявляется сигнал (правый на рисунке), связанный с комптоновским рассеянием.

на электронах внутренних оболочек. На первом графике комптоновское рассеяние отсутствует, θ =0°. На втором при θ =60°появляется пик, связанный с комптоновским рассеянием, далее, с ростом угла рассеяния при θ = 90° пик сдвигается по горизонтальной оси пропорционально увеличению длины волны (согласно формуле), что соответствует его лучшей разрешимости.

Очевидно, что для наблюдения эффекта необходимо выполнение двух условий 1. Длина волны рассеиваемого излучения должна быть сравнима с комптоновским

излучение рентгеновского диапазона 2. Рассеяние должно происходить на электронах минимально связанных с ядрами

атомов мишени, то есть на электронах, максимально удаленных от ядра атома. Для выполнения этого условия экспериментаторами выбирались характерные веществамишени.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник