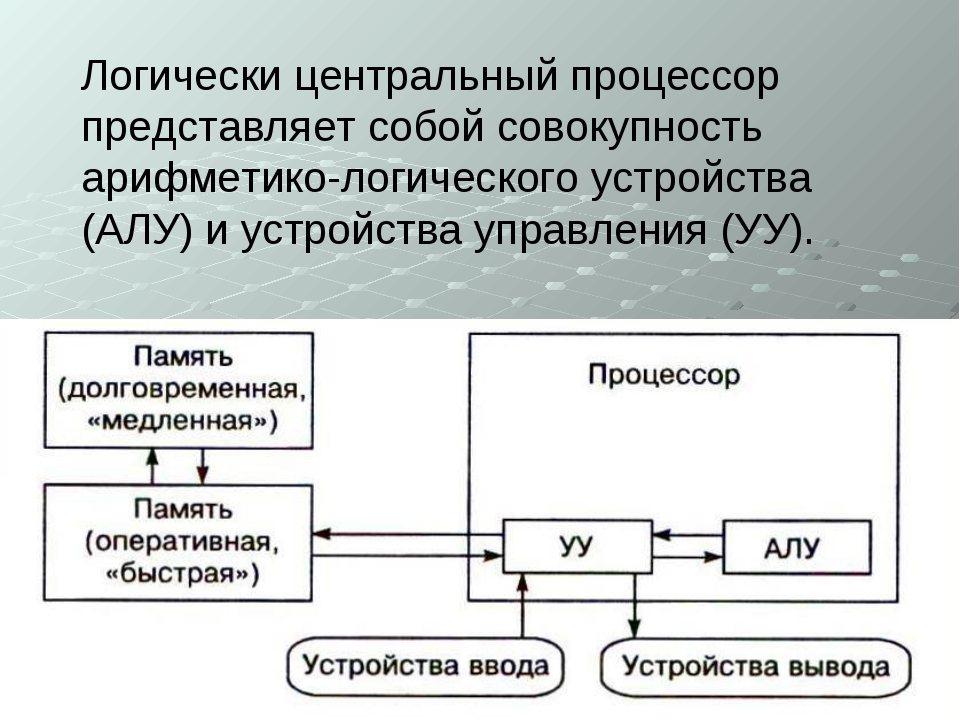
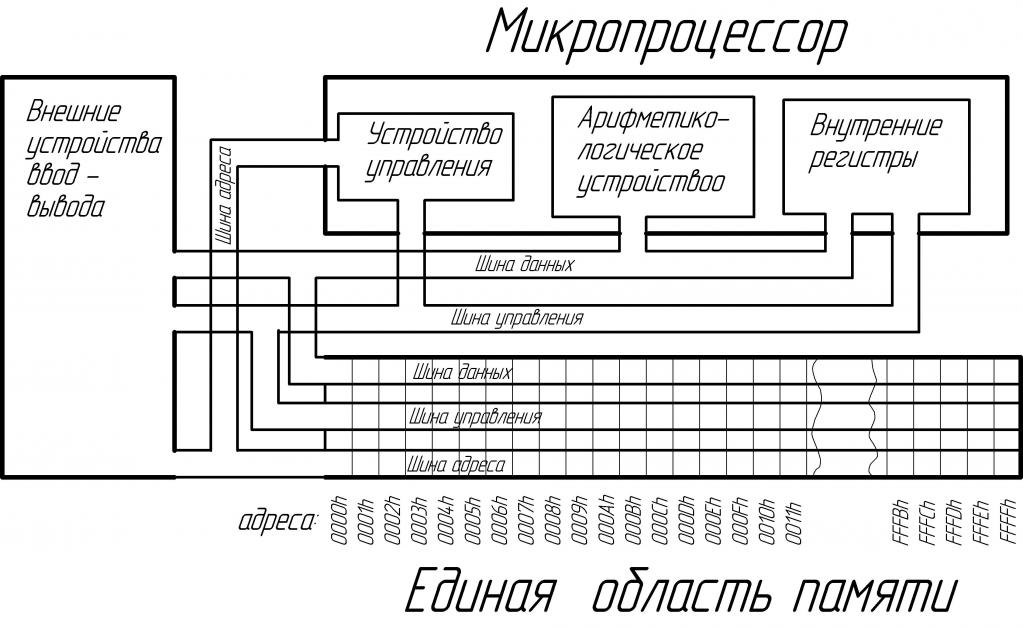
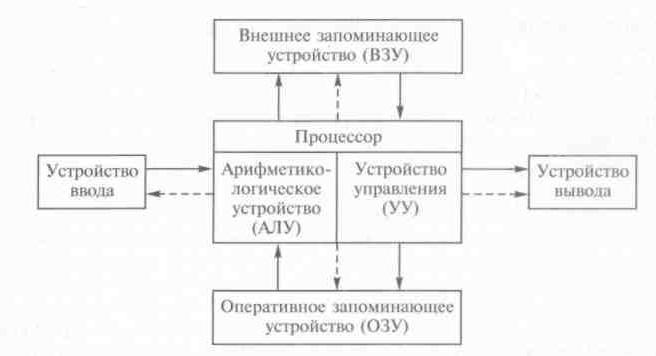
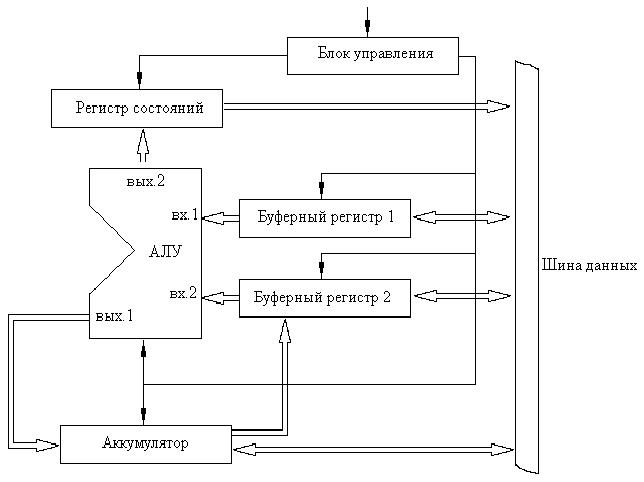
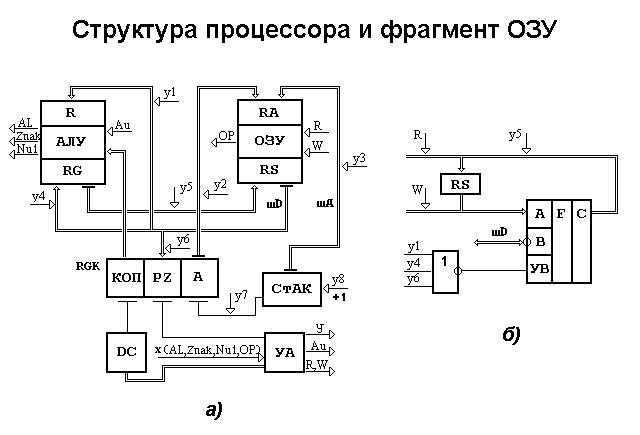
какие действия выполняет арифметико логическое устройство алу
Арифметико-логическое устройство
АЛУ реализует важную часть процесса обработки данных. Она заключается в выполнении набора простых операций. Операции АЛУ подразделяются на три основные категории: арифметические, логические и операции над битами. Арифметической операцией называют процедуру обработки данных, аргументы и результат которой являются числами (сложение, вычитание, умножение, деление. ). Логической операцией именуют процедуру, осуществляющую построение сложного высказывания (операции И, ИЛИ, НЕ. ). Операции над битами обычно подразумевают сдвиги.
Содержание
История создания
Разработчик компьютера ENIAC, Джон фон Нейман, был первым создателем АЛУ. В 1945 году он опубликовал первые научные работы по новому компьютеру, названному EDVAC (Electronic Discrete Variable Computer). Годом позже он работал со своими коллегами над разработкой компьютера для Принстонского института новейших исследований (IAS). Архитектура этого компьютера позже стала прототипом архитектур большинства последующих компьютеров. В своих работах фон Нейман указывал устройства, которые, как он считал, должны присутствовать в компьютерах. Среди этих устройств присутствовало и АЛУ. Фон Нейман отмечал, что АЛУ необходимо для компьютера, поскольку оно гарантирует, что компьютер будет способен выполнять базовые математические операции включая сложение, вычитание, умножение и деление
Структура АЛУ
АЛУ состоит из регистров, сумматора с соответствующими логическими схемами и элемента управления выполняемым процессом. Устройство работает в соответствии с сообщаемыми ему именами (кодами) операций, которые при пересылке данных нужно выполнить над переменными, помещаемыми в регистры.
Арифметико-логическое устройство функционально можно разделить на две части :
Часть операционных регистров является программно-доступной, то есть они могут быть адресованы в команде для выполнения операций с их содержимым. К ним относятся : сумматор, индексные регистры, некоторые вспомогательные регистры.
Остальные регистры программно-недоступные, так как они не могут быть адресованы в программе. Операционные устройства можно классифицировать по виду обрабатываемой информации, по способу обработки информации и логической структуре.
АЛУ может оперировать четырьмя типами информационных объектов: булевскими (1 бит), цифровыми (4 бита), байтными (8 бит) и адресными (16 бит). В АЛУ выполняется 51 различная операция пересылки или преобразования этих данных. Так как используется 11 режимов адресации (7 для данных и 4 для адресов), то путем комбинирования «операция/ режим адресации» базовое число команд 111 расширяется до 255 из 256 возможных при однобайтном коде операции.
Классификация АЛУ
Операции в АЛУ
Выполняемые в АЛУ операции можно разделить на следующие группы:
Современные ЭВМ общего назначения обычно реализуют операции всех приведённых выше групп, а малые и микроЭВМ, микропроцессоры и специализированные ЭВМ часто не имеют аппаратуры арифметики чисел с плавающей точкой, десятичной арифметики и операций над алфавитно-цифровыми полями. В этом случае эти операции выполняются специальными подпрограммами. К арифметическим операциям относятся сложение, вычитание, вычитание модулей («короткие операции») и умножение и деление («длинные операции»). Группу логических операций составляют операции дизъюнкция (логическое ИЛИ) и конъюнкция (логическое И) над многоразрядными двоичными словами, сравнение кодов на равенство. Специальные арифметические операции включают в себя нормализацию, арифметический сдвиг (сдвигаются только цифровые разряды, знаковый разряд остаётся на месте), логический сдвиг (знаковый разряд сдвигается вместе с цифровыми разрядами). Обширна группа операций редактирования алфавитно-цифровой информации
Что такое арифметико-логическое устройство (АЛУ)
Что такое АЛУ? Арифметико-логическое устройство, одна из составляющих процессора. В статье мы приглашаем вас узнать принципы его действия, историю создания, основные характеристики, выполняемые операции, существующие классификации АЛУ.
Определение понятия
Современное многофункциональное АЛУ состоит сегодня из двух частей:
Набор выполняемых операций
Важно знать, какие операции должно исполнять АЛУ для того, чтобы обладать функциональной полнотой. Как правило, хватает четырех:
Если мы обратимся к первым арифметико-логическим устройствам, то увидим, что количество выполняемых ими операций ограничивалось 16-ю. Современные АЛУ способны выполнять сотни! Кстати, число операций и сегодня является важнейшей характеристикой данных устройств.
Классификация АЛУ
По способу представления информации:
По способу действий с операндами:
По применению систем исчисления:
По особенностям использования узлов и элементов:
По временным характеристикам:
По характеристике устройства управления:
Основные функции
Арифметико-логическое устройство является составной частью процессора компьютера. АЛУ будет выполнять следующие функции:
Главные количественные характеристики
Составные части арифметико-логического устройства (ОУ и УУ) определяют количественные характеристики всей системы АЛУ. В частности, это следующее:
Главные качественные характеристики
Арифметико-логическое устройство (АЛУ) является составной частью процессора. Это определяет его важнейшие качественные характеристики:
История возникновения
Создателем арифметико-логических устройств считается Джон фон Нейман, разработчик компьютеров ЭНИАК (электронных числовых вычислителей).
Архитектура этого изобретения («архитектура фон Неймана») в дальнейшем стала базой, прототипом архитектур и большей части последующих компьютеров. В своих работах ученый указывал на наличие устройств, которые, по его мнению, являются обязательными для каждого компьютера. Среди них было упомянуто АЛУ. Фон Нейман считал, что арифметико-логическое устройство необходимо, потому что позволяет выполнять системе математические базовые операции. Как то: сложение и вычитание, умножение и деление.
Внутреннее устройство АЛУ
Мы уже разобрали, что условно АЛУ можно разделить на две части:
При этом условно состав АЛУ также подвергается следующей градации:
Сами микрокоманды делятся на две категории:
Функции регистров АЛУ
Чтобы иметь представление о работе АЛУ, нам нужно поближе познакомиться с функциями его регистров:
Теперь предлагаем вам обратиться к конкретным алгоритмам работы АЛУ.
Операция сложения
Функционально арифметико-логическое устройство будет состоять из Регистра 1, Регистра 2, сумматора и схемы управления.
Теперь распишем арифметическую операцию по тактам:
Операция вычитания
Давайте рассмотрим выполнение еще одной простой арифметической операции:
Операции в устройстве
Структурно–функциональная организация арифметическо–логического устройства (АЛУ)
Назначение и состав АЛУ
Арифметическо–логическое устройство предназначено:
● для реализации стандартного набора арифметических и логических операций над 16–разрядными операндами X, Y, а также многоцикловой операции деления с использованием двух имеющихся примитивов. Ниже приводится список стандартных функций АЛУ: R=X+Y сложение X и Y R=X+Y+CI сложение X и Y с переносом; R=X–Y вычитание Y из X; R=X–Y–CI–1 вычитание Y из X с заемом; R=Y–X вычитание X из Y; R=Y–X–CI–1 вычитание X из Y с заемом; R=–X арифметическое отрицание X;
R=–Y арифметическое отрицание Y; R=Y+1 инкремент Y; R=Y–1 декремент Y; R= PASS X результат равен операнду X; R= PASS Y результат равен операнду Y; R=0 (PASS 0) очистить результат; R=ABS X абсолютное значение X; R=X AND Y логическое умножение; R=X OR Y логическое сложение; R=X XOR Y сложение по модулю 2; R=NOT X логическое отрицание X; R=NOT Y логическое отрицание Y;
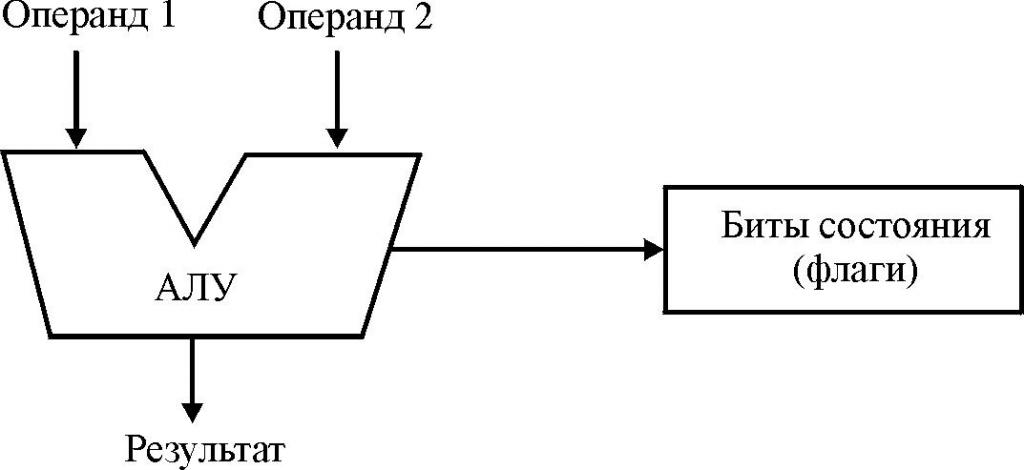
● для выдачи информации о состоянии процессора. После выполнения операции АЛУ генерирует (или обновляет) шесть флагов:
В состав блока АЛУ входят (рис. 8.3.1):
Путем установки бита AR_SAT = 1 (позиция MSTAT.3 в регистре режима и статуса процессора) регистр результата AR переводится в режим насыщения, в котором его содержимое при переполнении (флаг AV = 1) фиксирует:
Операция деление в АЛУ
Для операции деления в АЛУ используется дополнительная сдвиговая логика, не показанная на рис. 8.3.1. Деление может быть знаковым и беззнаковым. Деление беззнаковых чисел реализуется с помощью команды–примитива DIVQ, при выполнении которой формируется один бит частного за процессорный цикл. Шестнадцатикратное выполнение команды DIVQ позволяет получить 16 бит частного.
При делении знаковых чисел предварительно определяется знак частного с помощью другой команды–примитива DIVS.
После этого 15–кратное использование команды–примитива DIVQ позволяет получить значение частного с одинарной точностью. 
Для рассмотрения операции определении знака частного (DIVS) воспользуемся схемой на рис. 8.3.2. В исходном состоянии:
В исходном состоянии:
Для получения правильного результата при делении двух целых чисел (делимое в формате 32.0 и делитель в формате 16.0) необходимо предварительно сдвинуть делимое влево на один разряд, т. е. перевести делимое в формат 1.31.
Назначение и состав умножителя-акумулятора в АЛУ
Умножитель–акумулятор МАС позволяет выполнить умножение двух 16–разрядных операндов (Х*Y), умножение с накоплением суммы и разности (MR+X*Y; MR–X*Y), очистку результата MR, где MR — содержимое регистра результата. 
В состав умножителя–аккумулятора входят (рис. 8.3.4):
Основные режимы умножителя-аккумулятора АЛУ
Умножитель–аккумулятор обеспечивает выполнение операций в двух стандартных режимах:
Операция переполнения в АЛУ
После выполнения каждой операции в сумматоре–вычитателе формируется флаг переполнения MV, который заносится в позицию ASTAT.6 регистра арифметического статуса ASTAT (табл. 8.3.7). Флаг переполнения устанавливается (MV = 1) в том случае, если результат на выходе сумматора–вычитателя, интерпретируемый как число с дополнением до 2, пересекает 32–битную границу. В этом случае 9 старших (знаковых) разрядов 40–битного регистра результата не равны одновременно 0 или 1.
Операция насыщения в АЛУ
Эта операция выполняется при установленном флаге переполнения (MV = 1) в регистре арифметического статуса ASTAT (табл. 8.3.7). В результате операции содержимое регистра результата MR принимает максимальное:
Операция округления в АЛУ
С помощью опции RND аккумулятор позволяет округлять 40–битный результат до 16–битного. Округленный результат передается в регистр MR или MF. При использовании регистра MR округленный 16–битный результат содержится в регистре MR1. Содержимое регистров MR2, MR1 можно рассматривать как результат, округленный до 24 бит. 
Устройство сдвига.
Назначение и состав устройства сдвига
Устройство сдвига SHIFTER предназначено для выполнения сдвиговых операций 16–разрядных операндов, включающих арифметические и логические сдвиги, нормализацию и денормализацию, определение экспоненты. Устройство сдвига содержит (рис. 8.3.5):
Принцип работы устройства
Сдвиг входного 16–разрядного операнда осуществляется под действием контрольного кода и сигнала HI/LO, поступающих соответственно на входы С и R сдвигового массива.
Контрольный код представляет собой 8–разрядный операнд, указывающий направление сдвига и число разрядов, на которое следует произвести сдвиг. Положительное значение операнда указывает на левый сдвиг (или сдвиг вверх), отрицательное — на правый сдвиг (или сдвиг вниз). Контрольным кодом могут служить содержимое регистра SE в прямой и инверсной форме или непосредственно команда.
Сигнал HI/LO определяет начальную точку сдвига: в режиме HI сдвиги производятся относительно SR1 (верхней половины выходного поля); в режиме LO — относительно SR0 (нижней половины). Устройство сдвига заполняет все биты 32–битного результата справа от позиции операнда нулями, слева — битом расширения X, который может быть взят из трех источников: знаковый бит операнда, бит переноса АС из регистра ASTAT и 0.
Детектор экспоненты (степени) позволяет выделить степень из входного 16–разрядного операнда и может находиться в трех состояниях, по–разному интерпретирующих степень входного операнда:
Ниже с использованием примеров рассмотрены особенности выполнения операций определения экспоненты блока, немедленных сдвигов, денормализации и нормализации.
Определение экспоненты (степени) блока
Эта операция, выполняемая с помощью команды EXPANDJ, позволяет определить степень самого большого по масштабу числа из массива чисел. При определении экспоненты используется регистр блочных операций SB. В исходном состоянии регистр SB загружен числом –16 (SB = –16), которое поступает на один из входов цифрового компаратора (см. рис. 8.3.5). На другой вход компаратора с выхода детектора экспоненты подается значение экспоненты EXP1 первого элемента массива. Если EXP1>SB, то значение EXP1 загружается в регистр SB, т. е. SB = EXP1.
В противном случае содержимое SB остается неизменным.
Подобным образом обрабатываются последующие элементы массива. После обработки всех элементов массива регистр SB будет содержать наибольшую степень, значение которой лежит в пределах от –15 до 0. Отметим, что операция определения экспоненты является просмотровой операцией. Для выполнения операции нормализации необходимо скопировать содержимое регистра SB в регистр экспоненты SE. В табл. 8.3.2 приведен пример определения экспоненты блока из трех элементов. Из табл. 8.3.2 следует, что степень самого большого из приведенных чисел массива составляет –3.
Команда немедленные сдвиги
С помощью команд немедленного сдвига выполняются операции логического или арифметического сдвига влево (вверх)/вправо (вниз) на требуемое число разрядов. В командах определено направление и размер сдвига. Сдвиг происходит под действием контрольного кода в виде 8–битного знакового числа, который берется из команды. Регистр экспоненты SE в немедленных сдвигах не задействован.
Примеры. Рассмотрим случай, когда входной операнд в виде 16–разрядного двоичного кода 10110110 10100011 (0xB6A3) загружается в регистр операндов SI.
Логические сдвиги
Денормализация
Денормализация числа — это его сдвиг на заданное число разрядов, которое хранится в регистре экспоненты SE. Поэтому при денормализации контрольный код берется из регистра SE, а не из команды как при немедленных сдвигах. Фактически денормализация преобразует число с плавающей точкой в число с фиксированной точкой. Пример. Покажем особенности этой операции на примере денормализации числа с двойной точностью. Пусть содержимое регистра SE = –3. В этом случае необходимо выполнить в два этапа (в любой последовательности):
Нормализация
Нормализация числа в виде дополнительного кода — ото такой сдвиг числа, при котором остается только один знаковый бит. При выполнении операции нормализации фиксируется число разрядов, на которое сдвигается операнд. Поэтому операцию нормализации можно считать как преобразование числа с фиксированной точкой в число с плавающей точкой, имеющее порядок и мантиссу. На первом этапе нормализации чисел с одинарной точностью по команде EXP определяется порядок числа, на втором по команде NORM реализуется требуемый сдвиг.
Обе команды выполняются с использованием модификаторов HI или LO, а команда NORM дополнительно распознает также модификаторы PASS и OR.
При выполнении команды NORM используется содержимое регистра экспоненты SE со знаком минус (рис. 8.3.5), чтобы произвести сдвиг в нужную сторону. Нормализация чисел с двойной точностью выполняется по приведенной схеме, однако на первом этапе старшая половина числа обработать первой. При определении порядка старшей половины числа значение порядка загружается в регистр экспоненты SE. Младшая половина числа изменит содержимое SE только в том случае, когда все биты старшей половины являются знаковыми, т.е. при SE = –15. В этом случае в регистр SE будет загружен порядок (–16…–31, табл. 8.3.1) младшей половины числа. Зафиксированное в SE значение порядка используется на втором этапе для сдвига обоих частей числа с двойной точностью. При этом порядок обработки (старшей или младшей половины числа) может быть выбран любой с помощью модификаторов HI и LO. Первая половина числа нормализуется без модификатора OR, вторая половина числа — с модификатором OR, чтобы получить правильный результат.
Арифметико-логическое устройство
Материал из ПИЭ.Wiki
АЛУ реализует важную часть процесса обработки данных. Она заключается в выполнении набора простых операций. Операции АЛУ подразделяются на три основные категории: арифметические, логические и операции над битами. Арифметической операцией называют процедуру обработки данных, аргументы и результат которой являются числами (сложение, вычитание, умножение, деление. ). Логической операцией именуют процедуру, осуществляющую построение сложного высказывания (операции И, ИЛИ, НЕ. ). Операции над битами обычно подразумевают сдвиги.
Содержание
История создания
Разработчик компьютера ENIAC, Джон фон Нейман, был первым создателем АЛУ. В 1945 году он опубликовал первые научные работы по новому компьютеру, названному EDVAC (Electronic Discrete Variable Computer). Годом позже он работал со своими коллегами над разработкой компьютера для Принстонского института новейших исследований (IAS). Архитектура этого компьютера позже стала прототипом архитектур большинства последующих компьютеров. В своих работах фон Нейман указывал устройства, которые, как он считал, должны присутствовать в компьютерах. Среди этих устройств присутствовало и АЛУ. Фон Нейман отмечал, что АЛУ необходимо для компьютера, поскольку оно гарантирует, что компьютер будет способен выполнять базовые математические операции включая сложение, вычитание, умножение и деление
Структура АЛУ
АЛУ состоит из регистров, сумматора с соответствующими логическими схемами и элемента управления выполняемым процессом. Устройство работает в соответствии с сообщаемыми ему именами (кодами) операций, которые при пересылке данных нужно выполнить над переменными, помещаемыми в регистры.
Арифметико-логическое устройство функционально можно разделить на две части :
Часть операционных регистров является программно-доступной, то есть они могут быть адресованы в команде для выполнения операций с их содержимым. К ним относятся : сумматор, индексные регистры, некоторые вспомогательные регистры.
Остальные регистры программно-недоступные, так как они не могут быть адресованы в программе. Операционные устройства можно классифицировать по виду обрабатываемой информации, по способу обработки информации и логической структуре.
АЛУ может оперировать четырьмя типами информационных объектов: булевскими (1 бит), цифровыми (4 бита), байтными (8 бит) и адресными (16 бит). В АЛУ выполняется 51 различная операция пересылки или преобразования этих данных. Так как используется 11 режимов адресации (7 для данных и 4 для адресов), то путем комбинирования «операция/ режим адресации» базовое число команд 111 расширяется до 255 из 256 возможных при однобайтном коде операции.
Классификация АЛУ
Операции в АЛУ
Выполняемые в АЛУ операции можно разделить на следующие группы:
Современные ЭВМ общего назначения обычно реализуют операции всех приведённых выше групп, а малые и микроЭВМ, микропроцессоры и специализированные ЭВМ часто не имеют аппаратуры арифметики чисел с плавающей точкой, десятичной арифметики и операций над алфавитно-цифровыми полями. В этом случае эти операции выполняются специальными подпрограммами. К арифметическим операциям относятся сложение, вычитание, вычитание модулей («короткие операции») и умножение и деление («длинные операции»). Группу логических операций составляют операции дизъюнкция (логическое ИЛИ) и конъюнкция (логическое И) над многоразрядными двоичными словами, сравнение кодов на равенство. Специальные арифметические операции включают в себя нормализацию, арифметический сдвиг (сдвигаются только цифровые разряды, знаковый разряд остаётся на месте), логический сдвиг (знаковый разряд сдвигается вместе с цифровыми разрядами). Обширна группа операций редактирования алфавитно-цифровой информации
Арифметико-логическое устройство (АЛУ)
В курсе цифровые устройства изучается внутреннее устройство двоичных сумматоров, способных осуществить суммирование многоразрядных кодов. Однако кроме операции суммирования часто требуется осуществлять вычитание двоичных кодов. Двоичные коды, при помощи которых можно записывать отрицательные числа уже рассматривались ранее. Там же было показано, что при использовании дополнительных кодов операцию вычитания двух положительных чисел можно заменить операцией суммирования положительного и отрицательного числа, при этом получение отрицательного числа из положительного числа является элементарной операцией. Для этого необходимо проинвертировать число и прибавить к нему 1.
Схема вычитателя числа A из числа B приведена на рисунке 1, а схема вычитателя числа B из числа A приведена на рисунке 2.
Рисунок 1. Схема вычитателя A − B
Рисунок 2. Схема вычитателя B − A
В данных схемах инвертирование числа производится блоком логических инверторов, а прибавление единицы производится подачей питания на вход переноса сумматора PI. Если же потребуется в процессе вычислений изменять арифметическую операцию, то в структурную схему вычислительного устройства можно ввести коммутатор (мультиплексор). Такая схема арифметического устройства приведена на рисунке 3.
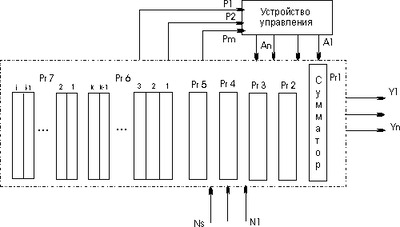
Рисунок 3. Структурная схема арифметического устройства.
В приведённой на рисунке 3 схеме используются четырёхвходовые мультиплексоры, для управления каждым из которых достаточно двух бит. То есть для управления всей схемы в целом достаточно четырёх проводов управления. Попытаемся построить таблицу операций, которые будет выполнять арифметико-логическое устройство (АЛУ), схема которого приведена на рисунке 3. На результат операции будет влиять вход переноса сумматора PI, поэтому этот вход тоже включим в состав кода, управляющего схемой АЛУ. Операции, которые выполняются арифметической схемой в зависимости от поданного на управляющие линии кода, приведены в таблице 1.
Таблица 1. Коды математических операций арифметического устройства
| Номер строки | Управляющий код | Выполняемая операция | ||||
|---|---|---|---|---|---|---|
| K0 | K1 | K2 | K3 | PI | ||
| 0 | 0 | 0 | 0 | 0 | 0 | S = A + B |
| 1 | 0 | 0 | 0 | 0 | 1 | S = A + B + 1 |
| 2 | 0 | 0 | 0 | 1 | 0 | S = B − A − 1 |
| 3 | 0 | 0 | 0 | 1 | 1 | S = B − A |
| 4 | 0 | 0 | 1 | 0 | 0 | S = B − 1 |
| 5 | 0 | 0 | 1 | 0 | 1 | S = B |
| 6 | 0 | 0 | 1 | 1 | 0 | S = B |
| 7 | 0 | 0 | 1 | 1 | 1 | S = B + 1 |
| 8 | 0 | 1 | 0 | 0 | 0 | S = A − B − 1 |
| 9 | 0 | 1 | 0 | 0 | 1 | S = A − B |
| 10 | 0 | 1 | 0 | 1 | 0 | S = −A − B − 2 |
| 11 | 0 | 1 | 0 | 1 | 1 | S = −A − B − 1 |
| 12 | 0 | 1 | 1 | 0 | 0 | S = −B − 2 |
| 13 | 0 | 1 | 1 | 0 | 1 | S = −B − 1 |
| 14 | 0 | 1 | 1 | 1 | 0 | S = −B − 1 |
| 15 | 0 | 1 | 1 | 1 | 1 | S = −B |
| 16 | 1 | 0 | 0 | 0 | 0 | S = A − 1 |
| 17 | 1 | 0 | 0 | 0 | 1 | S = A |
| 18 | 1 | 0 | 0 | 1 | 0 | S = −A − 2 |
| 19 | 1 | 0 | 0 | 1 | 1 | S = −A − 1 |
| 20 | 1 | 0 | 1 | 0 | 0 | S = −2 |
| 21 | 1 | 0 | 1 | 0 | 1 | S = −1 |
| 22 | 1 | 0 | 1 | 1 | 0 | S = −1 |
| 23 | 1 | 0 | 1 | 1 | 1 | S = 0 |
| 24 | 1 | 1 | 0 | 0 | 0 | S = A |
| 25 | 1 | 1 | 0 | 0 | 1 | S = A + 1 |
| 26 | 1 | 1 | 0 | 1 | 0 | S = −A − 1 |
| 27 | 1 | 1 | 0 | 1 | 1 | S = −A |
| 28 | 1 | 1 | 1 | 0 | 0 | S = −1 |
| 29 | 1 | 1 | 1 | 0 | 1 | S = 0 |
| 30 | 1 | 1 | 1 | 1 | 0 | S = 0 |
| 31 | 1 | 1 | 1 | 1 | 1 | S = +1 |
Проанализируем эту таблицу. Если на все управляющие входы подать низкий потенциал (Управляющий код равен 0000), то к входу сумматора будут подключены коды A и B без инверсии. В этом случае будет производиться операция суммирования. Эта ситуация отображена первыми двумя строками таблицы выполняемых операций. Операция вычитания осуществляется второй, третьей, восьмой и девятой строкой. В этом случае один из операндов поступает на вход сумматора через блок инверторов. Правда для получения дополнительного кода не хватает единицы, но её можно подать на вход переноса сумматора PI. Ещё одной часто используемой операцией является увеличение числа на единицу или уменьшение числа наединицу. Эти операции позволяют легко организовывать циклы в программе и переходить от предыдущего операнда к следующему. Такие операции могут быть выполнены при помощи кодов, записанных в строках четыре, семь, шестнадцать и двадцать пять. Кроме того, схема арифметического устройства может просто передавать на выход любой из входных кодов без изменения, что позволяет осуществлять копирование данных (суммирование с константой ноль) через это устройство без дополнительных схем коммутации.
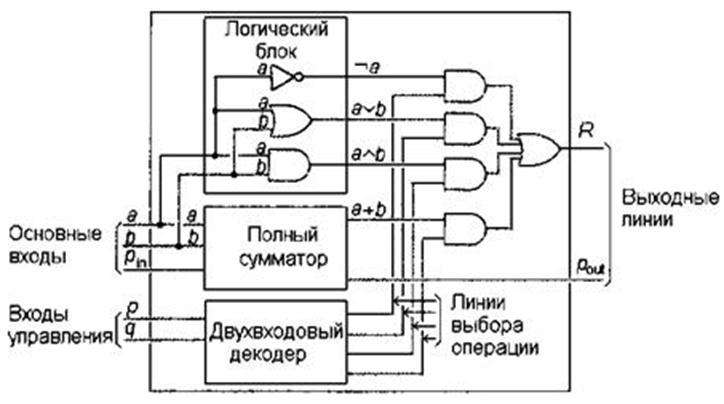
При небольшом изменении схемы такое устройство может быть преобразовано в схему, которая позволяет осуществлять не только арифметические, но и логические операции. Для этого нужно вести дополнительный коммутатор, который будет разрывать цепи переноса между разрядами. Эта управляющая цепь обычно называется M. Подобная схема реализована в микросхеме АЛУ К155ИП3 (иностранный аналог 74181). Ее внутренняя схема приведена на рисунке 4.
Рисунок 4. Схема арифметико-логического устройства (АЛУ) К155ИП3
Подчеркнём основную особенность полученного устройства. Арифметико-логические устройства позволяют выбирать вид выполняемой операции при помощи кода, подаваемого на специальные выводы микросхемы. Это позволяет программировать одно и то же устройство для выполнения различных функций. Разработка такого устройства позволило обменивать большую скорость выполнения отдельных операций на сложность реализуемого алгоритма, что, в конце концов, привело к разработке микропроцессорных систем. Развитие этих систем изменило окружающий нас мир.
Понравился материал? Поделись с друзьями!
Вместе со статьей «Арифметико-логическое устройство (АЛУ)» читают: