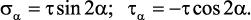какие деформации возникают в теле при сдвиге

Научная электронная библиотека

Лекция 6. СДВИГ (СРЕЗ)

Понятие чистого сдвига. Элементы конструкций, работающих в условиях чистого сдвига. Деформации, напряжения. Площадки чистого сдвига. Закон Гука при сдвиге. Условие прочности при сдвиге (срезе).

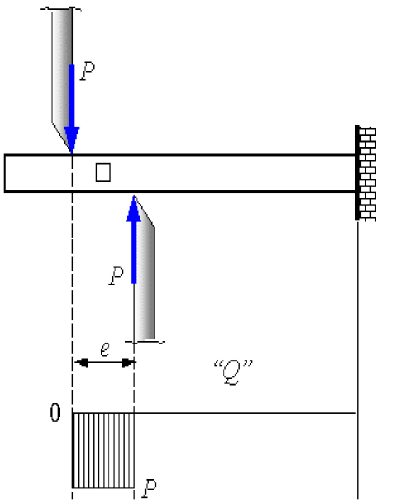
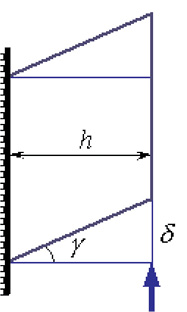
Рис. 16. Расчетная схема при сдвиге

Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.

Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.

Мера скольжения одного поперечного сечения относительно другого – касательные напряжения τ.

Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно. Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q = P, то касательные напряжения в любой точке этого сечения будут равны: T = Q/A = P/A.

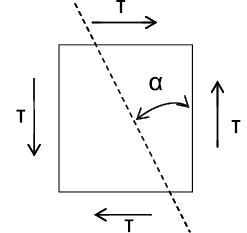
Рис. 17. Чистый сдвиг

При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол α с вертикальной исходной площадкой равны:

Касательные напряжения τ, приведенные на рис. 17, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45°.

При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.

Касательные напряженияτ измеряются в таких же единицах, что и нормальные напряжения: мегапаскалях, килоньютонах на квадратные сантиметры, килограммах силы на квадратный сантиметр (МПа, кН/см2, кгс/см2) и т.п.

В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ, называемую абсолютным сдвигом.

Рис. 18. Углы сдвига

Малый угол γ, на который изменится первоначально прямой угол, – относительный сдвиг, выражается в радианах. Угол сдвига γ пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге:

Зависимость между модулем сдвига и модулем Юнга:

Значение коэффициента Пуассона μ находится в пределах 0 ≤ μ ≤ 0,5.

Источник

Деформация сдвига

Одним из распространённых форм деформации является сдвиг отдельных слоёв изделия в вертикальной или горизонтальной плоскости. Такое смещение называется – деформация сдвига. Изменение положения может вызывать постепенное или резкое изменение первоначальной формы конструкции или отдельной детали. Виды деформации характеризуют порядок произведенного смещения и определяют порядок расчёта основных характеристик. В технической механике и сопромате рассматривают два вида деформации со сдвигом: плавное (смятие) и резкое (разрыв или срез).

Определение и общие сведения о деформации сдвига

Основным признаком, характеризующим деформацию сдвига, является сохранение постоянства объёма. Не зависимо от того, в каком направлении действуют силовые факторы этот параметр остаётся неизменным.

Примеры проявления деформации сдвига можно обнаружить при проведении различного рода работ. К таким случаям относятся:

При определённых условиях наблюдается чистый сдвиг. Он определяется как сдвиг, при котором на все четыре грани (например, прямоугольной детали) оказывают воздействие только напряжения, направленные по касательной к поверхности. В этом случае произойдёт плавный сдвиг всех слоёв детали от верхних к нижним слоям. Тогда внешняя сила изменяет форму детали, а объём сохраняется.

Для оценки величины сдвига и надёжности конструкции используют следующие параметры:

Расчёт и практическое измерение этих параметров необходимы для оценки устойчивости и целостности конструкции. Формула, позволяющая вычислить допустимые изменения, учитывает все воздействия на конкретные слои детали и всю конструкции в целом.

Основными итоговыми параметрами считаются абсолютный и относительный сдвиг. Абсолютным он называется при равенстве углу возникшего отклонения от первоначального положения грани. Относительный равен частному от деления величины отклонения к расстоянию между гранями, расположенными на противоположных сторонах. Во время упругой деформации сдвига одни элементы подвергаются сжатию, другие расширению.

В случае воздействия деформации величина угла считается пропорциональной внешней силе. Увеличение степени воздействия может превратить деформацию сдвига в срез. Это приведёт к разрушению не только элементов крепления (болтов, шпилек, заклёпок), но и всей детали.

Для наглядности изменения формы детали при деформации сдвига динамика процесса обозначается с помощью величины угла смещения и векторов возникающих напряжений. Действующая сила направлена в сторону смещения слоёв рассматриваемой детали.

В современных условиях угол сдвига измеряется различными техническими приборами. Основным прибором для измерения параметров смещения является тензомер. Эти приборы работают на различных физических принципах:

В этих приборах относительная деформация сдвига обрабатывается на современных вычислительных средствах с применением соответствующего программного обеспечения. Каждый метод обладает своими достоинствами и недостатками. Их применение зависит от поставленной задачи, технической и финансовой возможности.

Закон Гука

Основным соотношением, объединяющим физические параметры для описания протекающих процессов, является закона Гука для деформации сдвига. Этот закон позволят решить задачу нахождения угла отклонения грани объекта от исходного положения.

Небольшие напряжения вызывают углы отклонения, которые имеют небольшие величины. На итоговое значение влияют следующие параметры:

Различные материалы обладают своим значением модуля упругости. Он является величиной постоянной и определяет способность материала оказывать сопротивление возникающему сдвигу.

Вычисляют касательное напряжение на гранях с помощью закона Гука. Он справедлив для малых углов и представляет произведение модуля сдвига на величину угла. Согласно теории упругости он позволяет установить связь с модулем Юнга и коэффициентом Пуассона.

Графически действие закона Гука представлено прямой линией. В качестве уравнения этой линии может использоваться уравнение прямой с угловым коэффициентом подробно описанном в аналитической геометрии. Она проходит начало координат, выбранной системы отсчёта.

Напряжение при сдвиге

Воздействие внешней силы на грань приводит к возникновению в изделии изменения формы. Все напряжения делятся на две категории: нормальные и касательные. Нормальными считаются внутренние напряжения, возникающие в различных слоях изделия, подверженного деформации.

Напряжения и деформации при сдвиге описываются с применением аналитических выражений и графических изображений. Общее состояние описывается пространственным (трёхкоординатным) напряжением. Если в конкретном случае можно выявить сечения, в которых оба вида напряжений равны нулю, можно перейти к более простым моделям описания этого процесса. Ими являются двухкоординатное (плоское) напряжённое состояние или линейное. Две последних модели являются частными случаями трёхкоординатного напряжённого состояния.

Касательные напряжения являются мерой скольжения одного поперечного слоя относительно другого. В изменениях на поверхности каждого слоя возникают только касательные напряжения. Для оценки полной картины деформации используют следующие теоретические положения:

Оценка их всех при деформации смещения позволят оценить прочность конструкции.

Расчёты на прочность при сдвиге

Оценка прочностных характеристик изделий производится для определения наступления трёх моментов деформации:

Расчёт на прочность необходим для определения условий наступления каждого из видов. На практике для более наглядной оценки характеристик прочности и стойкости к деформации решают существующие аналитические выражения и изображают эпюры отражающие направления воздействия различных видов напряжений.

Получение численных характеристик возможно благодаря применению разработанных методов решения систем дифференциальных уравнений. Уточнение аналитических выражений производится на основе принятых гипотез.

Расчёт допустимых напряжений производится на основании первой, третьей и четвёртой гипотезы прочности. Каждая из гипотез принимается для различных материалов, обладающих своими физико-механическими характеристиками.

Прочность находиться на каждом из этапов разработки конкретной детали. Сначала вычисляют величины допустимых напряжений и угол отклонения на предварительном (проверочном) этапе. Это позволяет определить их уровни, величины и направление приложенных сил. После этого приступают к проектированию. На этом этапе производится выбор материала детали и крепёжных элементов с учётом необходимой прочности каждого элемента конструкции. На конечном этапе ещё раз проверяют допустимые нормы нагрузки и способность готовой детали выдерживать допустимую и дополнительную нагрузку, то есть определяют запас прочности.

Наиболее показательными являются расчёты для чистого сдвига. В этом случае при расчёте рассматривают следующие аспекты решения задачи:

На математическом и физическом этапе рассмотрения поставленной задачи применяются следующие основные расчетные выражения и допущения:

Наиболее важный практический интерес представляют два случая – смятие и разрыв.

В первом случае происходит пластическая деформация детали, когда интенсивность возникших напряжений превышает предел текучести выбранного материала. Размеры такой деформации зависят от характера и интенсивности действия внешних сил, показателей прочности материала, изменения температурного режима.

При интенсивности воздействия, превышающем прочность материала, происходит разрыв. Оба эти процесса приводят к нарушению механических соединений деталей (например, метизов, заклёпок, втулок).

Разработанные методы расчёта прочности позволяют проектировать и изготавливать детали с заданием, превышающим этот предел. Это позволяет существенно повысить надёжность и долговечность всей конструкции. В настоящее время разработан стройный математический аппарат создания моделей допустимой деформации. Его реализуют с применением созданных программных средств, которые позволяют получить числовые характеристики прочности и построить графические изображения эпюр в формате 3D графики.

Источник

Виды деформаций деталей: растяжение, сжатие, сдвиг, кручение, изгиб

материал предоставил СИДОРОВ Александр Владимирович

Деформация – изменение формы, размеров тела под действием приложенных к нему сил.

Линейная деформация – изменение линейных размеров тела, его рёбер. Линейные размеры тела могут изменяться одновременно в одном, двух или трёх взаимно перпендикулярных направлениях, что соответствует линейной, плоской и объёмной деформации. Линейная деформация, как правило, сопровождается изменением объёма тела.

Угловая деформация – изменение угловых размеров тела, углов наклона его граней. В результате угловой деформации происходит взаимное смещение граней. При этом изменяется только форма тела, объём сохраняется неизменным.

Линейная деформация связана преимущественно с действием нормальных напряжения, угловая – с действием касательных напряжений. [1]

Растяжение (сжатие) – деформация, возникающая под действием в поперечном сечении только продольной (растягивающей или сжимающей) силы.

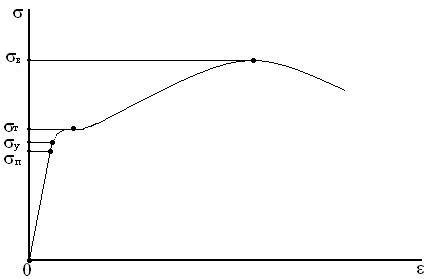
Напряжение вдоль оси прямо пропорционально растягивающей (сжимающей) силе и обратно пропорционально площади поперечного сечения. При упругой деформации соотношение между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их на коэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами (рисунок 1). [2]

Рисунок 1 – Диаграмма растяжения

Сдвиг – деформация, характеризующаяся взаимным смещением параллельных слоёв материала под действием сил, приложенных касательно к его поверхности, при неизменном расстоянии между слоями (рисунок 2).

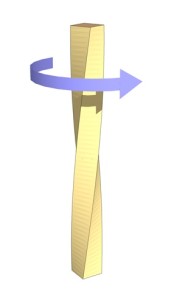
Кручение – деформация, характеризующаяся взаимным поворотом поперечных сечений тела под действием пары сил (момента) в этих сечениях (рисунок 3).

Рисунок 3 – Кручение

Изгиб – деформация, при которой происходит изменение кривизны осей тела под действием изгибающих моментов в поперечных сечениях (рисунок 4).

Источник

Деформация сдвига — определение, общие сведения, расчеты

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 июля 2014; проверки требуют 2 правки.

У этого термина существуют и другие значения, см. Сдвиг.

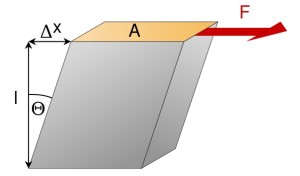
Сдвиг — в сопротивлении материалов — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно) — одна боковая грань смещается относительно другой (противоположной) грани.

Относительная деформация сдвига определяется по формуле:

где Δx — абсолютный сдвиг параллельных слоёв тела относительно друг друга; l — расстояние между слоями (для малых углов )

Определение и общие сведения и деформации сдвига

При деформации разные части тела перемещаются не одинаково.

При небольших деформациях сдвига угол () сдвига пропорционален приложенной деформирующей силе. При больших деформациях сдвига может произойти разрушение тела, которое называют срезом.

Деформацию сдвига испытывают все балки в месте опоры, болты, соединяющие детали. Срез при деформации сдвига можно наблюдать при работе ножниц, пилы и т.д.

Величину называют абсолютным сдвигом. Отношение к расстоянию между противоположными гранями называется относительным сдвигом. Если деформация мала, то относительный сдвиг равен углу сдвига. Угол сдвига выражают в радианах. Относительную деформацию при сдвиге можно определить как:

где h — расстояние между слоями. Для малых углов сдвига можно считать, что:

Библиографическое описание:

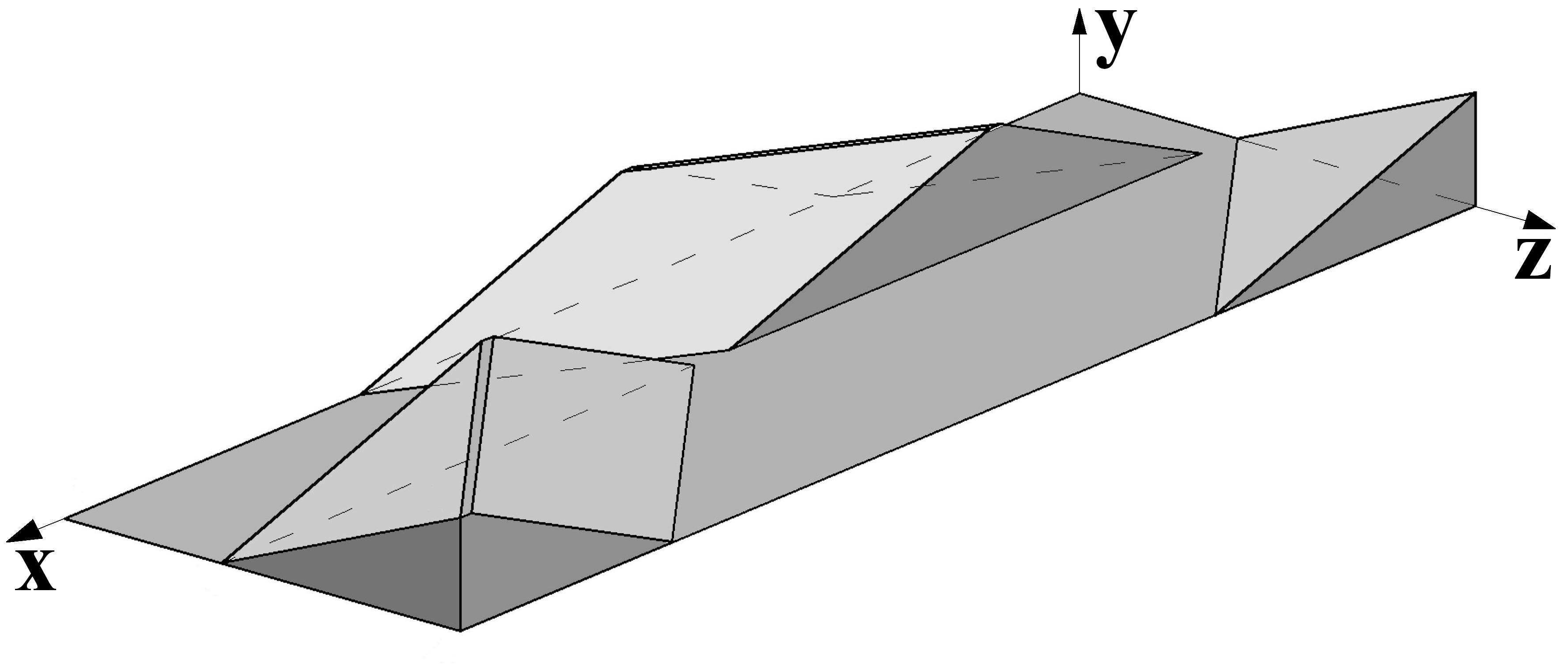
Рис. 1 Развёртка двухлопастного ротора

Рис. 2 Развёртка лопасти ротора – 2 вида (1, 2, 3 – зоны деформирования материала)

Зона 1: При деформации полимера вдоль оси x получим:

В случае движения стенки камеры вдоль оси z:

Результирующая суммарная деформация сдвига в зоне 1 находится по формуле:

Разделив выражение (3) на объём данной зоны получим окончательную формулу для нахождения суммарной деформации сдвига в данной зоне:

Зона 2: В данном случае будет решаться только первая задача из предыдущих двух, т.к. материал в этой зоне не испытывает продольного воздействия, а подвергается деформации только в направлении вращения. Деформация сдвига в направлении вращения ротора выразится в форме уравнения:

Разделив выражение (5) на объём второй зоны получим окончательную формулу для нахождения суммарной деформации сдвига в данной зоне:

Зона 3: Суммарная величина смесительного воздействия, которому подвергается материал в данной зоне за время t, определяется следующим образом :

Величина суммарной деформации сдвига на всей лопасти будет равна алгебраической сумме величин суммарных деформаций сдвига в трёх рассмотренных зонах:

где γ1, γ2, γ3 – величины суммарных деформаций сдвига в зонах лопасти 1, 2 и 3, соответственно.

Для второй лопасти ротора вычисления будут идентичными, изменится только длина лопасти lzв угол наклона винтовой линииαz, в связи с чем изменится скорость движения по оси z и объёмы соответствующих зон V’1 и V’2, а, следовательно, и значения деформаций сдвига в первой и второй зоне – γ1’ и γ2’. Величина суммарной деформации сдвига на всей лопасти будет равна:

где γ1’, γ2’, γ3 – величины суммарных деформаций сдвига в зонах лопасти 1, 2 и 3, соответственно.

Таким образом, на втором роторе величина суммарной деформации сдвига будет находиться таким же способом, как и на первом, изменится только величина скорости: U2 = f·U, где f – фрикция. Формула для нахождения величины суммарной деформации сдвига на втором роторе:

В итоге, для нахождения величины суммарной деформации сдвига действующей на материал во время процесса смешения и диспергирования во всём объёме смесительной камеры необходимо суммировать величины полученных деформаций сдвига на каждом роторе, используя при этом коэффициент, учитывающий объёмный расход, приходящийся на каждый ротор, и перекрытие зон деформации:

где q – коэффициент, учитывающий объёмный расход, приходящийся на каждый ротор, и перекрытие зон деформации.

Была получена следующая зависимость для нахождения суммарной деформации сдвига:

где V – объём перерабатываемой смеси, см3; n – индекс течения, nср – средняя частота вращения заднего и переднего ротора, об/мин; l1 и l2 – длина длинного и короткого гребней ротора, см; Dгр – диаметр гребня ротора по кромке, см; F – коэффициент; h0 – зазор между кромкой гребня ротора и камерой, см; δ – ширина кромки, см.

где i– число элементов, на которые разбивается деформируемый объём или ширина зоны деформации материала, в зазоре между ротором и камерой; Dк – внутренний диаметр камеры смесителя, см; hi – зазор между гребнем ротора и камерой для i-ого элемента, см; fi– площадь сечения i-ого элемента, см2.

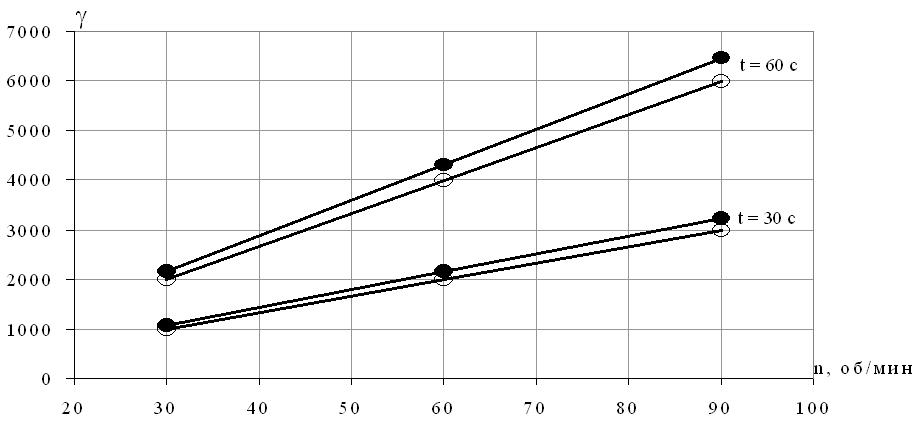
Рис. 3 Зависимость суммарной деформации сдвига от времени процесса смешения

Рис. 4 Зависимость суммарной деформации сдвига от частоты вращения рабочих органов смесителя

Установлено, что при прочих равных параметрах (nср = 75 об/мин; Dк = 4,78 см; l1 = 4,5 см; l2 = 2,6 см; l = 6,5; V = 100см3; n = 0,3) (рис. 5) на расхождение в моделях оказывает значительное влияние величина минимального зазора между стенкой камеры и кромкой ротора h0­. Это расхождение становиться наиболее интенсивным в областях, где h0­ Закон Гука при сдвиге

Для небольших напряжений угол сдвига прямо пропорционален величине касательного напряжения ():

где G – модуль сдвига или модуль упругости второго рода;

где — сила упругости, которая действует вдоль слоя тела; S – площадь рассматриваемого слоя. Или для величины абсолютного сдвига закон Гука можно записать как:

Модуль сдвига – постоянная величина, которая характеризует способность материала сопротивляться сдвигу. В международной системе единиц модуль сдвига измеряется в паскалях.

Источник

Сила упругости

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Деформация

Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил

Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.

Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.

На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.

По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:

Сила упругости: Закон Гука

Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).

При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.

Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, про­порциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.

Закон Гука

Fупр = kx

Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]

Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.

Это равноценные обозначения — можно использовать любое удобное.

Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.

Задачка

На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?

Решение:

Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.

Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :

Тогда из Закона Гука выразим модуль удлинения лески:

Выражаем модуль удлинения:

Подставим числа, жесткость лески при этом выражаем в Ньютонах:

x=3/(0,3 * 1000)=0,01 м = 1 см

Ответ: удлинение лески равно 1 см.

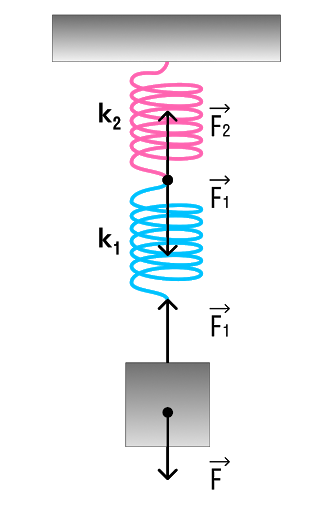
Параллельное и последовательное соединение пружин

В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.

Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.

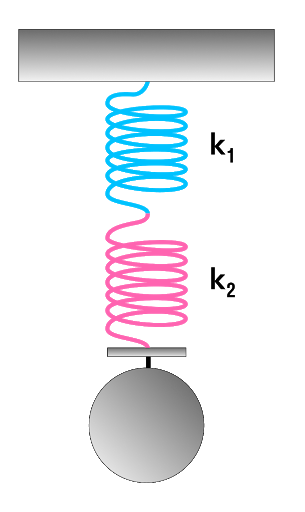
Последовательное соединение системы пружин

Последовательное соединение характерно наличием одной точки соединения пружин.

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

Коэффициент жесткости при последовательном соединении пружин

1/k = 1/k₁ + 1/k₂ + … + 1/k_i

k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

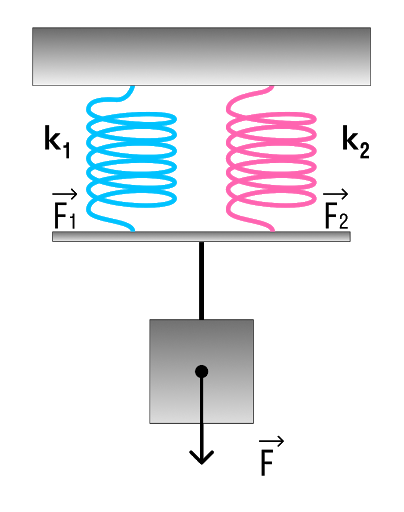
Параллельное соединение системы пружин

Последовательное соединение характерно наличием двух точек соединения пружин.

В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

Коэффициент жесткости при параллельном соединении пружин

k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]

Задачка

Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?

Решение:

а) Рассмотрим параллельное соединение пружин.

При параллельном соединении пружин общая жесткость

k = k₁ + k₂ = 100 + 200 = 300 Н/м

б) Рассмотрим последовательное соединение пружин.

При последовательном соединении общая жесткость двух пружин

1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015

k = 1000/15 = 200/3 ≃ 66,7 Н/м

График зависимости силы упругости от жесткости

Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.

Задачка 1

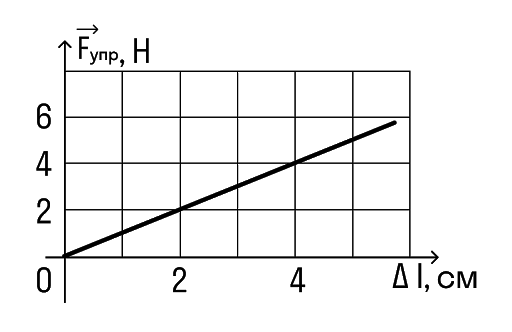
Определите по графику коэффициент жесткости тела.

Решение:

Из Закона Гука выразим коэффициент жесткости тела:

Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.

Например, возьмем вот эту точку.

В ней удлинение равно 2 см, а сила упругости 2 Н.

Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м

Ответ:жесткость пружины равна 100 Н/м

Задачка 2

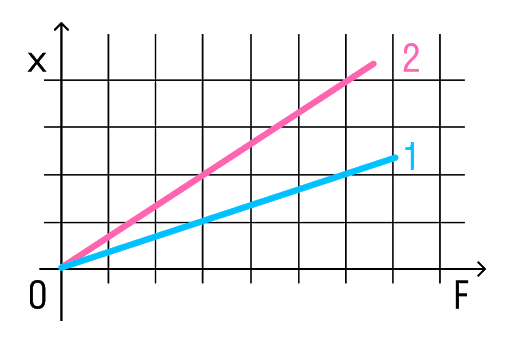
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.

Решение:

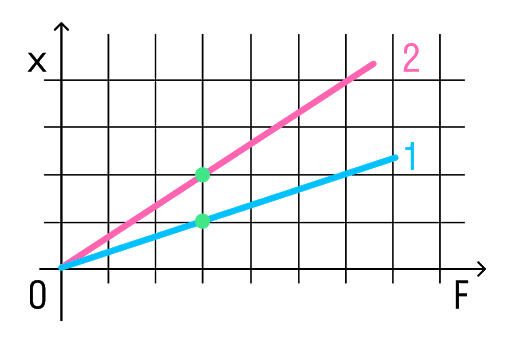
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.

Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.

Значит жесткость стальной проволоки больше.

Ответ: жесткость стальной проволоки больше медной.